Zad. 6. Rozkład LU macierzy kwadratowej z
częściowym wyborem elementu głównego
e-mail: [email protected]
tel.: 56611-3274
pokój: 485
http://www.fizyka.umk.pl/˜tecumseh/MN16/
Zadanie 6
Zmodyfikuj program dokonujący rozkładu LU macierzy metodą
Doolittle’a (albo Crouta) włączając częściowy wybór elementu
głównego.
Powtórka: rozkład LU
I A - nieosobliwa macierz kwadratowa n × n o elementach rzeczywistych
I det Ak 6= 0, gdzie Ak - macierz k × k utworzona z k początkowych wierszy i
kolumn macierzy A
I Rozkład A = LU, gdzie L - macierz trójkątna dolna n × n, U - macierz trójkątna
górna n × n, tzn.
(L)ij =
n
0 i <j
`ij i ­ j
(U)ij =
n
uij i ¬ j
0 i >j
I Mamy n2 równań na elementy macierzy A
aij =
n
X
r
X
k=1
k=1
(L)ik (U)kj =
`ik ukj ,
gdzie r = min(i, j)
I Jeżeli `ii = 1 albo uii = 1 dla i = 1, ..., n, to mamy w sumie do wyznaczenia n2
elementów macierzy L i U
Powtórka: schematy zwarte - metoda Doolittle’a
I Zakładamy, że `ii = 1 dla i = 1, ..., n
I Wykonujemy k = 1, ..., n kroków; w k-tym kroku
1. Wyznaczamy k-ty wiersz macierzy U (j ­ k)
akj =
k
X
⇒
`kp upj
ukj = akj −
k−1
X
`kp upj
j = k, k + 1, ..., n
p=1
p=1
2. Wyznaczamy k-tą kolumnę macierzy L (i > k)
aik =
k
X
p=1
`ip upk
⇒
`ik =
aik −
k−1
X
!
`ip upk
/ukk
i = k + 1, ..., n
p=1
I W pierwszym kroku znamy `11 = 1, co pozwala najpierw wyznaczyć pierwszy
wiersz macierzy U, a to z kolei pozwala wyznaczyć pierwszą kolumnę macierzy L
I W k-tym kroku znamy `kk = 1, k − 1 początkowych wierszy macierzy U i k − 1
początkowych kolumn macierzy L, to pozwala najpierw wyznaczyć k-ty wiersz
macierzy U, a to z kolei pozwala wyznaczyć k-tą kolumnę macierzy L
Powtórka: schematy zwarte - metoda Crouta
I Zakładamy, że uii = 1 dla i = 1, ..., n
I Wykonujemy k = 1, ..., n kroków; w k-tym kroku
1. Wyznaczamy k-tą kolumnę macierzy L (i ­ k)
aik =
k
X
`ip upk
⇒
`ik = aik −
k−1
X
`ip upk
i = k, k + 1, ..., n
p=1
p=1
2. Wyznaczamy k-ty wiersz macierzy U (j > k)
akj =
k
X
p=1
`kp upj
⇒
ukj =
akj −
k−1
X
!
`kp upj
/`kk
j = k + 1, ..., n
p=1
I W pierwszym kroku znamy u11 = 1, co pozwala najpierw wyznaczyć pierwszą
kolumnę macierzy L, a to z kolei pozwala wyznaczyć pierwszy wiersz macierzy U
I W k-tym kroku znamy `kk = 1, k − 1 początkowych wierszy macierzy U i k − 1
początkowych kolumn macierzy L, to pozwala najpierw wyznaczyć k-tą kolumnę
macierzy L, a to z kolei pozwala wyznaczyć k-ty wiersz macierzy U
Częściowy wybór elementu głównego - motywacje
I
Dokonać rozkładu LU macierzy
1 1
1
A = 2 −2 2
3 3 −3
I
Zamieniamy wiersze w macierzy A
1 1
1
A0 = 3 3 −3
2 −2 2
Dokonać rozkładu LU tej macierzy
I
Czy w obydwu przypadkach udało się dokonać rozkładu LU?
Częściowy wybór elementu głównego - metoda Doolittle’a
I k-ty krok metody Doolittle’a
1. Wyznaczamy k-ty wiersz macierzy U (j ­ k)
ukj = akj −
k−1
X
`kp upj
j = k, k + 1, ..., n
p=1
2. Wyznaczamy k-tą kolumnę macierzy L (i > k)
`ik =
aik −
k−1
X
!
`ip upk
/ukk
i = k + 1, ..., n
p=1
I Problemy: ukk = 0 lub |ukk | ∼ 0 (np. „śmieci numeryczne”)
I Wybór elementu głównego:
1 wyznaczamy k-ty wiersz macierzy U
1a przed wyznaczeniem k-tej kolumny macierzy L szukamy w k-tym wierszu
macierzy U elementu o maksymalnej wartości bezwzględnej, tzn.
max |ukj | ⇒ ukjmax
j=k,...,n
1b zamieniamy w macierzy U kolumny k i jmax
2 wyznaczamy k-tą kolumnę macierzy L
Częściowy wybór elementu głównego - metoda Doolittle’a
I Uzyskujemy rozkład A = LU0 , gdzie U0 jest macierzą trójkątną górną, w której
poprzestawialiśmy kolumny
I Macierz U0 można przedstawić jako U0 = UP, gdzie U jest macierzą trójkątną
górną, a P jest macierzą permutacji
I Rozkład macierzy A przyjmuje wtedy następującą postać
A = LUP
I Pojedynczą zamianę kolumn i i j w macierzy U można przedstawić jako iloczyn
macierzy UPij , gdzie macierz Pij jest macierzą jednostkową n × n, w której
zamieniono wiersze i z j
I W każdym kroku metody Doolittle’a dokonujemy (co najwyżej) pojedynczej
zamiany kolumn w macierzy U, dlatego końcowy wynik, czyli macierz U0 ,
możemy przedstawić w następujący sposób
U0 = UP = UP1 P2 ...Pk ...Pn−1 Pn ,
gdzie Pk jest macierzą pojedynczej zamiany kolumn wykonanej w k-tym kroku
metody Doolittle’a
Częściowy wybór elementu głównego - metoda Crouta
I k-ty krok metody Crouta
1. Wyznaczamy k-tą kolumnę macierzy L (i > k)
`ik = aik −
k−1
X
`ip upk
i = k + 1, ..., n
p=1
2. Wyznaczamy k-ty wiersz macierzy U (j ­ k)
ukj =
akj −
k−1
X
!
`kp upj
/`kk
j = k, k + 1, ..., n
p=1
I Problemy: `kk = 0 lub |`kk | ∼ 0 (np. „śmieci numeryczne”)
I Wybór elementu głównego:
1 wyznaczamy k-tą kolumnę macierzy L
1a przed wyznaczeniem k-tego wiersza macierzy U szukamy w k-tej kolumnie
macierzy L elementu o maksymalnej wartości bezwzględnej, tzn.
max |`ik | ⇒ `imax k
i=k,...,n
1b zamieniamy w macierzy L wiersze k i imax
2 wyznaczamy k-ty wiersz macierzy U
Częściowy wybór elementu głównego - metoda Crouta
I Uzyskujemy rozkład A = L0 U, gdzie L0 jest macierzą trójkątną dolną, w której
poprzestawialiśmy wiersze
I Macierz L0 można przedstawić jako L0 = PL, gdzie L jest macierzą trójkątną
dolną, a P jest macierzą permutacji
I Rozkład macierzy A przyjmuje wtedy następującą postać
A = PLU
I Pojedynczą zamianę wierszy i i j w macierzy L można przedstawić jako iloczyn
macierzy Pij L, gdzie macierz Pij jest macierzą jednostkową n × n, w której
zamieniono kolumny i z j
I W każdym kroku metody Crouta dokonujemy (co najwyżej) pojedynczej
zamiany wierszy w macierzy L, dlatego końcowy wynik, czyli macierz L0 ,
możemy przedstawić w następujący sposób
L0 = PL = Pn Pn−1 ...Pk ...P2 P1 L,
gdzie Pk jest macierzą pojedynczej zamiany wierszy wykonanej w k-tym kroku
metody Crouta
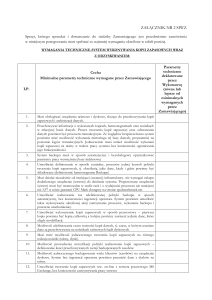
Do zrobienia - modyfikacja programu na rozkład LU
macierzy
1. Wczytać z wejścia wymiar n macierzy A i elementy tej macierzy
2. Dokonać rozkładu LU macierzy A metodą Doolittle’a (albo Crouta)
z częściowym wyborem elementu głównego
3. Wypisać na wyjściu macierze trójkątne L, U oraz macierz
permutacji P
4. Sprawdzić, czy A = LUP (albo A = PLU)
5. Porównać wyniki programu z wynikami z gotowych procedur (np.
„lu” Matlaba)