Temat: Składanie fal o różnych polaryzacjach
Niech dwie fale elektromagnetyczne mają jednakowe częstości (a więc zgodnie ze
wzorem (1.7c) także jednakowe liczby falowe i długości fal) i rozchodzą się w tym
samym kierunku. To oznacza, że czynniki są dla nich jednakowe, a więc jedynie E0
– wektorowe czynniki tych fal mogą różnić się, czyli fale mogą mieć różne
polaryzacje i amplitudy. Tylko takie fale będziemy tu rozpatrywać.
Pokażemy, że dowolnie spolaryzowaną falę określoną przez wektor E0, można
przedstawić w postaci superpozycji dwóch fal spolaryzowanych ,
(2.1)
Fale ,
mogą być spolaryzowane liniowo, albo kołowo o przeciwnych obiegach i
wreszcie spolaryzowane eliptycznie także o przeciwnych obiegach. To zaś oznacza,
że każdy z tych ruchów stanowi bazę fizyczną opisu stanu polaryzacji światła.
Udowodnimy pierwsze z tych twierdzeń, czyli pokażemy, że dowolnie
spolaryzowaną falę można przedstawić w postaci superpozycji dwóch fal
spolaryzowanych liniowo. Przyjmijmy zatem, że falę określa wektorowa amplituda .
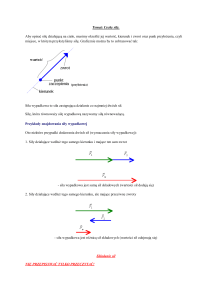
Niech OA i OB będą dwoma nierównoległymi osiami, leżącymi w tej samej
płaszczyźnie co wektory Ej (j = 1,2),
Rys. 2.1
przecinającymi się w punkcie O (rys. 2.1). Niech będzie wektorem leżącym na osi
OA, natomiast – wektorem leżącym na osi OB. Wektory , zawsze można wybrać
tak, aby wektor E1 był sumą wektorów ,
.
(2.2a)
.
(2.2b)
Podobnie
Stąd
(2.3)
Ponieważ więc fale o amplitudach wektorowych
są liniowo spolaryzowane. Najczęściej przyjmujemy, że osie OA, OB są do siebie
prostopadłe. Ponieważ na wektor E0 i na osie OA, OB nie nakładaliśmy żadnych
ograniczeń możemy powiedzieć, że fale spolaryzowane liniowo tworzą bazę
fizyczną.
Przyjmijmy, że spełnione są następujące warunki:
,.
(2.4a,b)
Rozpatrzymy wektor
.
(2.5)
Zbadajmy odpowiedź na pytanie jakie warunki muszą spełniać wektory i stałe aby
wektor E (2.5) określał polaryzację liniową, tj. aby spełniona była relacja
.
(2.6)
Po podstawieniu równań (2.4a,b) i (2.6) do równania (2.5) otrzymamy związek
.
(2.7)
Jest on spełniony jeżeli wszystkie wektory są równoległe , albo .
Niech wektory , znajdujące się po prawej stronie równania (2.1) odpowiadają
polaryzacji kołowej, tzn. zgodnie ze związkami (1.27) ich składowe spełniają warunki
(2.8)
Wektor (2.1) można teraz przedstawić w postaci
.
(2.9)
Jak widać
.
(2.10a,b)
Gdy to zgodnie z warunkiem (1.27a) mamy to fala jest spolaryzowana kołowo.
Natomiast gdy
to warunek (1.27a) nie jest spełniony, a więc fala nie jest
spolaryzowana kołowo. By ustalić polaryzację fali odpowiadającej wektorowi (2.9)
zbadamy iloczyn . Mamy
(2.11)
Gdy wektory są równoległe to ze wzoru (2.11) wynika, że . Mamy więc do czynienia
z falą kołowo, albo eliptycznie spolaryzowaną. Obliczymy i . Mamy . Obliczyć jest
nieco trudniej
.
Wykorzystamy wzór (1.10a), wtedy
.
Na podstawie wzoru (1.23a,b) stwierdzamy, że gdy to fala jest spolaryzowana eliptycznie. Kryterium (1.26) pozwala ustalić obieg. Po wykorzystaniu tożsamości
wektorowej (1.10b) i po uwzględnieniu własności prostopadłości wektorów natężenia
pola elektrycznego do kierunku propagacji fali otrzymamy
Zatem gdy
Natomiast
warunek równoległości składników wektora
prowadzi do
następującej relacji
Skąd wynika, że fala będąca złożeniem dwóch fal kołowo spolaryzowanych o
przeciwnych obiegach jest liniowo spolaryzowana wtedy gdy
§ 2.2 Wektory Jonesa
Niech wersory określają kierunki osi x, y i z kartezjańskiego układu współrzędnych.
Wybierzemy oś z kartezjańskiego układu współrzędnych tak, by była ona równoległa
do kierunku propagacji fali: , osie x i y leżą w płaszczyźnie stałej fazy i są dowolnie
zorientowane. Dla takiego wyboru układu współrzędnych
.
Zapiszemy wektor E w postaci macierzowej
Oczywiście można zastąpić ten wektor przez wektor dwuelementowy, dla którego
wprowadzimy specjalne oznaczenie , zatem
.
Wektor
będziemy nazywali zupełnym wektorem Jonesa [1]. Natomiast gdy w
składowych pominiemy wspólny czynnik fazowy to będziemy mówili o wektorze
Jonesa, dla którego będziemy używali oznaczenia Diraca , zatem
.
Dla wektora otrzymanego z
(2.12a)
w wyniku operacji sprzężenia hermitowskiego
wprowadzimy nowe oznaczenie:. Zgodnie z tym określeniem
.
(2.12b)
Górny wskaźnik T oznacza operację transponowania, natomiast * oznacza
sprzęganie liczb zespolonych.
Rozpatrzymy dwa wektory
biliniową
i , można im przyporządkować skalar – formę
(2.13)
Jak widać, zgodnie z równaniem (1.11b), gęstość energii dla fali reprezentowanej
przez wektor jest proporcjonalna do iloczynu
(2.14)
Ponieważ
znika wtedy i tylko wtedy gdy znika wektor pola elektrycznego, więc
wtedy i tylko wtedy gdy . Zatem biliniowa forma (2.14) określa iloczyn skalarny.
Łatwo zauważyć, że falom odpowiadającym wektorom
,,
odpowiadają te same gęstości energii. Iloczyn
określa normę
wektora . Nie
znikający wektor Jonesa jest unormowany do jedności.
Dla wektorów Jonesa będziemy także używali innego oznaczenia
.
§ 2.3 Przykłady wektorów Jonesa
Rozpatrzymy przykłady wektorów Jonesa dla różnych polaryzacji.
A)
Znajdziemy
wektor
Jonesa
dla
światła
spolaryzowanego
kołowo
prawoskrętnie. Dla jego oznaczenia użyjemy skrótu RCP (od angielskich słów right
circular polarized). Ponieważ w tym przypadku dla wybranego przez nas układu
współrzędnych związek (1.27a) przyjmuje postać
,
to wektorowi odpowiada wektor Jonesa
Ostatni wektor można przekształcić
gdzie jest odpowiednią składową wektora pola elektrycznego w bazie stanów kołowo
spolaryzowanych. Wektor jest unormowany do jedności
Drugi wektor bazy stanów kołowo spolaryzowanych – ma postać
.
Bez trudu można sprawdzić, że wektory i są ortogonalne, tj. .
B)
Zajmiemy się następnie zadaniem odwrotnym do powyżej rozpatrzonego.
Określimy polaryzację fali odpowiadającej wektorowi Jonesa
.
Odpowiadają mu następujące składowe wektora pola elektrycznego: ; ,
(2.15)
Zatem
wektorowi Jonesa (2.15) odpowiadają wektory , . Sprawdzamy rodzaj polaryzacji jaka
odpowiada temu wektorowi. Obliczymy iloczyn wektorowy znalezionych wektorów
Z kryterium (1.26a) wynika, że fala nie jest liniowo spolaryzowana. Jak widać mamy
do czynienia z polaryzacją kołową albo eliptyczną. Łatwo sprawdzić, że oraz, że , .
Zatem . Na podstawie kryterium (1.23) stwierdzamy, że mamy do czynienia z falą
spolaryzowaną eliptycznie. Zbadajmy kierunek obiegu tej elipsy. Ponieważ
na
podstawie kryterium (1.26b,c) stwierdzamy, że mamy do czynienia z falą
prawoskrętnie, eliptycznie spolaryzowaną, dla której użyjemy symbolu ERP: .
Oczywiście powinniśmy jeszcze określić charakterystyki odpowiedniej elipsy. Jednak
nie będziemy tu zajmowali się tym zagadnieniem (por. [2])
C) Trzecie zagadnienie jest bardziej ogólne. Pokażemy, że wektory
,.
(2.16a,b)
określają fale eliptycznie spolaryzowane o przeciwnych skrętnościach albo dwie fale
liniowo spolaryzowane w kierunkach prostopadłych. W tym celu znajdziemy wektory
natężenia pola elektrycznego odpowiadające wektorom Jonesa
1) Niech , wtedy
Zbadajmy iloczyny . Mamy
,.
Gdy
obydwie fale charakteryzowane przez wektory Jonesa
są spolaryzowane
eliptycznie. Zbadajmy jeszcze kierunki obiegów (skrętności). Ponieważ
skrętności są przeciwne. Ostatecznie stwierdzamy, że gdy to
Obliczymy jeszcze iloczyn skalarny wektorów
W ten sposób doszliśmy do ważnego wniosku: Wektory o przeciwnych skrętnościach
odpowiadające tej samej polaryzacji są do siebie prostopadłe.
2) Natomiast gdy to . To oznacza, że obydwu wektorom odpowiadają fale liniowo
spolaryzowane, a więc spełnione są relacje , , co równoważne jest następującym
związkom, które spełniają liczby m1, m2, n1, n2: Łatwo sprawdzić, że – odpowiednie
fale są liniowo spolaryzowane w kierunkach prostopadłych do siebie. Liczby m1, m2,
n1, n2 są zgodne z warunkiem . Stwierdzamy więc, że w przypadku polaryzacji
liniowej dwóm ortogonalnym wektorom Jonesa odpowiadają prostopadłe do siebie
kierunki polaryzacji (wektory są prostopadłe).
§ 2.4 Liniowa przestrzeń Jonesa
Wektory Jonesa tworzą 2D przestrzeń liniową nad ciałem liczb zespolonych, bowiem
spełnione są następujące warunki:
(a) Dla operacja dodawania jest przemienna:
(b) Dla operacja dodawania ma własność łączności:
.
(c) Dla dowolnych liczb zespolonych a, b i dowolnego wektora
spełnione jest
pierwsze prawo rozdzielności:
.
(d) Dla dowolnej liczby zespolonej a, oraz spełnione jest drugie prawo rozdzielności:
.
(e) Dla dowolnych liczb zespolonych a, b oraz zachodzi związek .
Dla wektorów należących do zdefiniowaliśmy iloczyn skalarny (2.13). Dlatego
jest przestrzenią unitarną. Będziemy przestrzeń
nazywali przestrzenią Jonesa.
Niezależnym ruchom fizycznym odpowiadają niezależne liniowo
wektory z
przestrzeni Jonesa. Ponieważ każdą bazę w można zortogonalizować, będziemy
używać baz ortogonalnych.
§ 2.5 Uogólnienie
Zauważymy, że między sprzężonymi wektorami i (2.8a) i (2.8b) istnieje antyliniowy
związek taki, że [3]
,.
W dalszym ciągu każdemu stanowi
układu kwantowego (w naszym
konkretnym przypadku – stanowi polaryzacji) będziemy przypisywać wektor stanu
(nazwany przez Paula Diraca „bra”) i wektor (nazwany przez niego „ket”, bracket to
po angielsku nawias). Wektory stanu należą do przestrzeni liniowych (skończenie
albo nieskończenie wymiarowych – te ostatnie nazywane są przestrzeniami Hilberta).
Opis dwóch stanów i związany jest z wektorami bra i i wektorami ket , , z
których można utworzyć trzy iloczyny skalarne:
(a) liniowy w i antyliniowy w ; (b) liniowy w i antyliniowy w ; (c) – liniowy w i
antyliniowy w . Odwzorowanie F określone przez definicję (2.12a) wiąże możliwość
(a) i (c): . Stąd wynika, że gdy to , tj. jest liczbą rzeczywistą. Nałożymy jeszcze
dodatkowy warunek by gdy .
Każdej parze wektorów
i
reprezentującej stan
przypiszemy normę .
Wprowadzenie normy pozwala zmniejszyć dowolność istniejącą między stanami
układów kwantowych, a reprezentującymi je wektorami stanu. Przyjmiemy, że
wektory stanu są unormowane do jedności . Jak widać pozostaje jedynie dowolność
wyboru czynnika fazowego .
Literatura
[1] R.M.A. Azzam, N.M. Bashara, Ellipsometry and polarized light, North Holland ,
Amsterdam, 1977 (tłum. na j. ros. Ellipsometria i polarizowannyj swet, Mir, Moskwa,
1981, § 1.6.2.
[2] F.I. Fedorow, Optika anizotropnych sred, Izdatielstwo Akademii Nauk BSSR,
Minsk, 1958, R. III.
[3] B. W. Medwedew, Naczała teoreticzeskoj fiziki, Nauka, Moskwa, 1977, R. III.