11. czwórniki – klasyfikacja, równania

OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
11. CZWÓRNIKI – KLASYFIKACJA, RÓWNANIA
11.1. WIELOBIEGUNNIK A WIELOWROTNIK I CZWÓRNIK
Definicja1.
Jeśli: wielobiegunnik posiada parzystą liczbę zacisków (tzn. m=2n) zgrupowanych w n par
i dla każdej pary zacisków zachodzi związek (warunek regularności)
I k ' = −I k
(11.1)
to: - każdą tak określoną parę zacisków nazywamy "bramą", "wrotami";
- napięcie na bramie określone jest odpowiednią różnicą napięć zaciskowych tworzących tę bramę;
- wielobiegunnik nazywamy wówczas WIELOWROTNIKIEM bądź
WIELOBRAMNIKIEM.
Definicja 2.
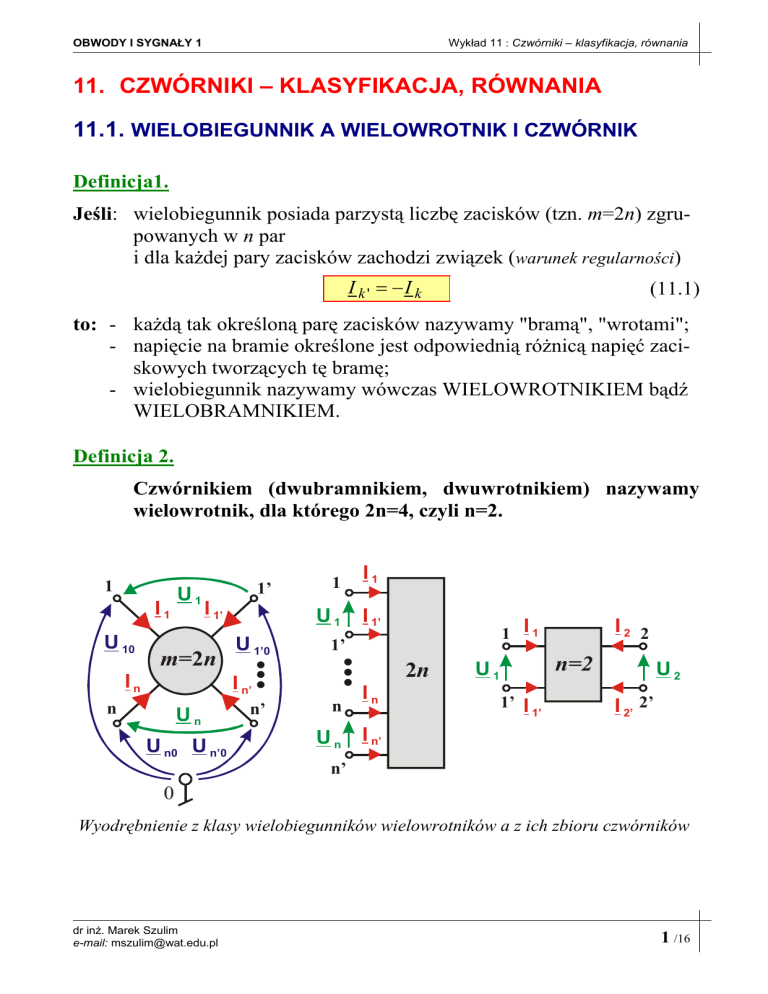
Czwórnikiem (dwubramnikiem, dwuwrotnikiem) nazywamy
wielowrotnik, dla którego 2n=4, czyli n=2.
1
I1
U 10
U1
1’
I 1’
m=2n
In
I n’
n
Un
U n0 U n’0
...
U 1’0
n’
1
I1
U1
I 1’
...
I
1 I1
1’
n
Un
2n
n
I2 2
n=2
U1
1’ I
1’
U2
I 2’ 2’
I n’
n’
0
Wyodrębnienie z klasy wielobiegunników wielowrotników a z ich zbioru czwórników
dr inż. Marek Szulim
e-mail: [email protected]
1 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
Każdy wielowrotnik a zatem i czwórnik można opisać wektorem napięć i
prądów związanych z jego wrotami i tak:
dla wielowrotnika
I = [I 1 , I 2 ,...., I n ] T , U = [U 1 , U 2 ,...., U n ] T
(11.2)
I = [I 1 , I 2 ] T , U = [U 1 , U 2 ] T
(11.3)
dla czwórnika
Przyjęte założenia pozwalają przedstawić czwórnik następująco
1
I1
I2
2
SLS
U1
1’
2’
U2
2’
Para zacisków 1-1’ – wrota pierwotne
2-2’ – wrota wtórne
Granicznymi stanami pracy każdej z bram są:
• stan jałowy – gdy prąd danej bramy jest równy zeru
(I1=0 lub I2=0)
• stan zwarcia – gdy napięcie danej bramy jest równe zeru
(U1=0 lub U2=0)
dr inż. Marek Szulim
e-mail: [email protected]
2 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
11.2. PODSTAWOWE RÓWNANIA (ZACISKOWE) CZWÓRNIKA
Równaniami czwórnika nazywamy zależności wiążące ze sobą
WIELKOŚCI ZACISKOWE, a więc prąd i napięcie wejściowe (I1, U1)
oraz prąd i napięcie wyjściowe (I2, U2).
Spośród czterech wielkości zaciskowych tylko dwie mogą być przyjęte jako niezależne, a dwie pozostałe jako zależne. Para wielkości niezależnych może być wybrana na sześć różnych sposobów, czwórnik można
zatem opisać jednym z sześciu rodzajów równań zaciskowych.
Para wielkości zaciskowych
RODZAJ RÓWNAŃ
ZALEŻNYCH
NIEZALEŻNYCH
1.
I1 , I2
U1, U2
ADMITANCYJNE
2.
U1, U2
I1, I2
IMPEDANCYJNE
3.
U 1 , I2
HYBRYDOWE
4.
I1 , U 2
I1, U2
U1, I2
5.
U 1 , I1
ŁAŃCUCHOWE
6.
U2, I12
U2, I2
U1, I1
dr inż. Marek Szulim
e-mail: [email protected]
HYBRYDOWE ODWROTNE
ŁAŃCUCHOWE ODWROTNE
3 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
1. RÓWNANIA ADMITANCYJNE CZWÓRNIKA
Przyjmujemy, że wielkościami niezależnymi są napięcia: pierwotne
U1 oraz wtórne U2. Odpowiada to następującemu sposobowi pobudzenia
czwórnika
1
I1
I2
U1
CZWÓRNIK
2
U2
2’
=
1’
1
U1
I 11
I 21
CZWÓRNIK
I 12
+
I 22
CZWÓRNIK
2
U2
2’
1’
I 1 = I 11 + I 12 ⎫
⎬
I 2 = I 21 + I 22 ⎭
gdzie:
I 11 = y11U 1
I 21 = y 21U 1
I 12 = y12U 2
I 22 = y 22U 2
Zatem równania admitancyjne czwórnika otrzymuje się jako:
I 1 = y11U 1 + y12U 2 ⎫⎪
⎬
I 2 = y 21U 1 + y 22U 2 ⎪⎭
dr inż. Marek Szulim
e-mail: [email protected]
(11.4)
4 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
I 1 = y11U 1 + y12U 2 ⎫⎪
⎬
I 2 = y 21U 1 + y 22U 2 ⎪⎭
(11.4)
lub w postaci macierzowej
⎡ I 1 ⎤ ⎡ y11
⎢I ⎥ = ⎢ y
⎣ 2 ⎦ ⎣ 21
y12 ⎤ ⎡U 1 ⎤
⎡U 1 ⎤
Y
⋅
=
⋅
⎢U ⎥
y 22 ⎥⎦ ⎢⎣U 2 ⎥⎦
⎣ 2⎦
(11.5)
Elementy macierzy admitancyjnej Y nazywamy parametrami admitancyjnymi czwórnika - można je wyznaczyć z układu równań 11.4
(jako stosunki prądów zaciskowych do napięć zaciskowych przy zwarciu
jednej z par zacisków):
y11 =
I1
U1
y12 =
U 2 =0
I1
U2
U 1 =0
admitancja dwójnika 1-1’ (od P)
I
y 21 = 2
U 1 U =0
admitancja wzajemna od W do P
I
y 22 = 2
U 2 U =0
admitancja wzajemna od P do W
I1
I2
admitancja dwójnika 2-2’ (od W)
I1
I2
2
1
2
1
1
CZWÓRNIK
U1
CZWÓRNIK
2’
1’
2
U2
2’
1’
Model obwodowy (schemat zastępczy) czwórnika dla równań (11.4/5)
I1
U1
dr inż. Marek Szulim
e-mail: [email protected]
I2
y11
y12 U 2
y21 U 1
y22
U2
5 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
2. RÓWNANIA IMPEDANCYJNE CZWÓRNIKA
Przyjmujemy, że wielkościami niezależnymi są prądy I1 oraz I2. Odpowiada to następującemu sposobowi pobudzenia czwórnika
1
I1
2
U1
CZWÓRNIK
I2
U2
2’
=
1’
1
I1
2
U 11 CZWÓRNIK U 21
+
I2
U 12 CZWÓRNIK U 22
2’
1’
U 1 = U 11 + U 12 ⎫
⎬
U 2 = U 21 + U 22 ⎭
gdzie:
U 11 = z11 I 1
U 21 = z 21 I 1
U 12 = z12 I 2
U 22 = z 22 I 2
Zatem równania impedancyjne czwórnika otrzymuje się jako:
U 1 = z11 I 1 + z12 I 2 ⎫
⎬
U 2 = z 21 I 1 + z 22 I 2 ⎭
(11.6)
lub w postaci macierzowej
⎡U 1 ⎤ ⎡ z11
⎢U ⎥ = ⎢ z
⎣ 2 ⎦ ⎣ 21
z12 ⎤ ⎡ I 1 ⎤
⎡ I1 ⎤
⋅
=
⋅
Z
⎢I ⎥
z 22 ⎥⎦ ⎢⎣ I 2 ⎥⎦
⎣ 2⎦
(11.7)
gdzie Z nazywamy macierzą impedancyjną czwórnika.
dr inż. Marek Szulim
e-mail: [email protected]
6 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
Elementami macierzy impedancyjnej (parametrami impedancyjnymi) są w ogólnym przypadku liczby zespolone mające wymiar impedancji
[Ω]. Można je wyznaczyć z równań 11.6 jako stosunki napięć zaciskowych do prądów zaciskowych przy rozwarciu jednej z par zacisków:
z11 =
U1
I1
= Z 1o
impedancja dwójnika 1-1’ (od P)
impedancja wejściowa pierwotna
rozwarciowa
U
z 21 = 2
I1
I 2 =0
I 2=0
I1
U2
2’
1’
I 1 =0
U2
I2
= Z 2o
I 1 =0
impedancja dwójnika 2-2’ (od W)
impedancja wejściowa wtórna rozwarciowa
I 1=0
I2
1
2
CZWÓRNIK
U1
U1
I2
impedancja wzajemna od W do P
z 22 =
impedancja wzajemna od P do W
1
z12 =
I 2 =0
2
CZWÓRNIK
U1
U2
2’
1’
Model obwodowy (schemat zastępczy) czwórnika dla równań (11.6/7)
U 1 = z11 I 1 + z12 I 2
U 2 = z 21 I 1 + z 22 I 2
I1
I2
z11
U1
dr inż. Marek Szulim
e-mail: [email protected]
⎫
⎬
⎭
z22
z12 I 2
z21 I 1
U2
7 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
3. RÓWNANIA HYBRYDOWE (szeregowo-równoległe)
Jeśli przyjmiemy, że wielkościami niezależnymi jest prąd pierwotny
I1 oraz napięcie wtórne U2 - otrzymamy równania hybrydowe (mieszane) czwórnika:
U 1 = h11 I 1 + h12 U 2 ⎫
⎬
I 2 = h 21 I 1 + h 22 U 2 ⎭
(11.8)
⎡ I1 ⎤
⎡U 1 ⎤ ⎡ h11 h12 ⎤ ⎡ I 1 ⎤
=
⋅
=
⋅
H
⎥ ⎢ ⎥
⎢U ⎥
⎢ I ⎥ ⎢h
⎣ 2 ⎦ ⎣ 21 h 22 ⎦ ⎣U 2 ⎦
⎣ 2⎦
(11.9)
lub w postaci macierzowej
gdzie H nazywamy macierzą hybrydową czwórnika.
Model obwodowy czwórnika dla równań (11.8)
I1
I2
h11
U1
h12 U 2
h11 =
U1
I1
h 21 =
I2
I1
dr inż. Marek Szulim
e-mail: [email protected]
[Ω]
U 2 =0
[-]
U 2 =0
h21I 1
h12 =
h 22 =
h22
U1
U2
I2
U2
U2
[-]
I 1 =0
[S]
I 1 =0
8 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
4. RÓWNANIA HYBRYDOWE ODWROTNE (równoległo-szeregowe)
Jeśli przyjmiemy, że wielkościami niezależnymi jest napięcie pierwotne U1 oraz prąd wtórny I2 - otrzymamy równania hybrydowe odwrotne (mieszane odwrotne) czwórnika:
I 1 = g 11U 1 + g 12 I 2 ⎫⎪
⎬
U 2 = g 21U 1 + g 22 I 2 ⎪⎭
(11.10)
lub w postaci macierzowej
⎡ I 1 ⎤ ⎡ g 11
⎢U ⎥ = ⎢ g
⎣ 2 ⎦ ⎣ 21
g 12 ⎤ ⎡U 1 ⎤
⎡U 1 ⎤
⋅
=
⋅
G
⎢I ⎥
g 22 ⎥⎦ ⎢⎣ I 2 ⎥⎦
⎣ 2⎦
(11.11)
gdzie G nazywamy macierzą hybrydową odwrotną czwórnika.
Schemat zastępczy czwórnika
I1
I2
g22
g11
U1
g11 =
I1
U1
g 21 =
U2
U1
dr inż. Marek Szulim
e-mail: [email protected]
g12 I 2
[S]
I 2 =0
[-]
I 2 =0
U2
g21U 1
g12 =
g 22 =
I1
I2
U2
I2
[-]
U 1 =0
[Ω]
U 1 =0
9 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
5. RÓWNANIA ŁAŃCUCHOWE CZWÓRNIKA
Równaniami łańcuchowymi opisujemy czwórnik wówczas, gdy znana jest para wielkości elektrycznych związanych z bramą wtórną
[U2, I2] a poszukujemy wielkości elektrycznych związanych z bramą pierwotną [U1, I1].
1
(- I 2)
I1
U1
kierunek
transmisji
2
U2
U 1 = a11U 2 + a12 (− I 2 )⎫
⎬
I 1 = a 21U 2 + a 22 (− I 2 ) ⎭
(11.12)
2’
1’
lub w postaci macierzowej
⎡U2 ⎤
⎡U 1 ⎤ ⎡ a11 a12 ⎤ ⎡ U 2 ⎤
A
=
⋅
=
⋅
⎥ ⎢
⎢ I ⎥ ⎢a
⎥
⎢− I ⎥
⎣ 1 ⎦ ⎣ 21 a 22 ⎦ ⎣− I 2 ⎦
⎣ 2⎦
(11.13)
gdzie A nazywamy macierzą łańcuchową czwórnika a jej elementy parametrami łańcuchowymi czwórnika (są one stosunkami wielkości zaciskowych pierwotnych do wtórnych, określonymi przy rozwarciu lub zwarciu zacisków wtórnych)
a11 =
a 21 =
U1
U2
I1
U2
dr inż. Marek Szulim
e-mail: [email protected]
[-]
a12 =
U1
− I2
a 22 =
I1
− I2
I 2 =0
[S]
I 2 =0
[Ω]
U 2 =0
[-]
U 2 =0
10 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
6. RÓWNANIA ŁAŃCUCHOWE ODWROTNE
Jeśli znane są wielkości związane z bramą pierwotną [U1, I1] a poszukujemy związanych z bramą wtórną [U2, I2], to równania typu (11.12)
przyjmują postać
1
(- I 1)
U1
I2
2
U2
kierunek
transmisji
U 2 = b11U 1 + b12 (− I 1 )⎫
⎬
I 2 = b 21U 1 + b 22 (− I 1 ) ⎭
(11.14)
2’
1’
lub w zapisie macierzowym
⎡U 2 ⎤ ⎡ b11 b12 ⎤ ⎡ U 1 ⎤
⎡ U1 ⎤
B
=
⋅
=
⋅
⎥ ⎢
⎢ I ⎥ ⎢b
⎥
⎢− I ⎥
⎣ 2 ⎦ ⎣ 21 b 22 ⎦ ⎣− I 1 ⎦
⎣ 1⎦
(11.15)
gdzie B nazywamy macierzą łańcuchową odwrotną czwórnika a jej
elementy parametrami łańcuchowymi odwrotnymi czwórnika (są one
stosunkami wielkości zaciskowych wtórnych do pierwotnych, określonymi
przy rozwarciu lub zwarciu zacisków pierwotnych)
b11 =
b 21 =
U2
U1
I2
U1
dr inż. Marek Szulim
e-mail: [email protected]
[-]
b12 =
U2
− I1
b 22 =
I2
− I1
I 1 =0
[S]
I 1 =0
[Ω]
U 1 =0
[-]
U 1 =0
11 /16
OBWODY I SYGNAŁY 1
PRZYKŁAD 11.1
Wykład 11 : Czwórniki – klasyfikacja, równania
Wyznaczyć parametry łańcuchowe czwórnika.
I1
I2
Z1
U1
Równania łańcuchowe (11.12):
Z3
U2
Z2
Dane:
Z1=j10Ω,
Z2=5Ω,
Z3=j10Ω.
⎧ U 1 = a11 U 2 + a12 (− I 2 )
⎪
⎨
⎪ I = a U + a (− I )
1
2
21 2
22
⎩
Wprowadzamy I |2 = − I 2
• a11 =
U1
gdy I |2 = 0
U2
Z1
U1
Z2
U2 =
a11 =
U2
Z2
U1
Z1 + Z 2
Z + Z2
Z
U1
= 1
= 1 + 1 = 1 + j 2 [−]
Z2
Z2
Z2
U1
Z1 + Z 2
dr inż. Marek Szulim
e-mail: [email protected]
12 /16
OBWODY I SYGNAŁY 1
•
a12 =
U1
I |2
Wykład 11 : Czwórniki – klasyfikacja, równania
|
I1
gdy U 2 = 0
I2
Z1
Z3
U1
Z2
z dzielnika prądu:
⎛Z + Z3 ⎞
⎟⎟ = I |2
I 1 = I |2 ⎜⎜ 2
⎝ Z2 ⎠
⎛ Z ⎞
U 1 = I |2 Z 3 + I 1 Z 1 = I |2 Z 3 + I |2 Z 1 ⎜⎜1 + 3 ⎟⎟
⎝ Z2 ⎠
I |2 =
a12
•
Z2
I1
Z2 + Z3
⇒
⎛
Z ⎞
⎜⎜1 + 3 ⎟⎟
⎝ Z2 ⎠
⎛ Z ⎞
I |2 Z 3 + I |2 Z 1 ⎜⎜1 + 3 ⎟⎟
⎝ Z 2 ⎠ = Z + Z + Z 1 Z 3 = (− 20 + j 20 ) [Ω ]
=
1
3
Z2
I |2
a 21 =
a 21 =
I1
I1
gdy I |2 = 0
U2
Z1
I1
1
=
= 0,2 [S ]
I1 Z 2 Z 2
U1
Z2
U2
U 2 = I1 Z 2
• a 22 = I |1 gdy U 2 = 0
I2
a 22 =
I1
Z2
I1
Z2 + Z3
dr inż. Marek Szulim
e-mail: [email protected]
=1+
Z3
= 1 + j 2 [−]
Z2
13 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
11.3. KLASYFIKACJA CZWÓRNIKÓW
Czwórnik pasywny i aktywny
Czwórnik nazywamy pasywnym, jeżeli przy początkowej energii
zgromadzonej w układzie równej zeru, całkowita energia dostarczona do
niego jest nieujemna:
t
∫ [u1(τ )i1(τ ) + u2 (τ )i2 (τ )]dτ ≥ 0
(11.16)
0
Niespełnienie tego warunku oznacza aktywność czwórnika.
W stanie ustalonym przy wymuszeniach harmonicznych:
•
czwórnik jest PASYWNY jeśli moc czynna pobierana przez wrota
czwórnika jest nieujemna dla każdej pary napięć i prądów zaciskowych
Re U 1 I 1* + Re U 2 I *2 ≥ 0
(11.17)
(
•
)
(
)
czwórnik jest AKTYWNY, jeśli istnieją takie wartości napięć i prądów zaciskowych, dla których pobierana przez wrota moc czynna jest
ujemna
Re U 1 I 1* + Re U 2 I *2 < 0
(11.18)
(
)
(
)
Czwórnik prawidłowy i nieprawidłowy
Czwórnik klasy SLS nazywamy czwórnikiem prawidłowym, jeśli posiada wszystkie macierze charakterystyczne.
Warunkiem koniecznym i wystarczającym prawidłowości czwórnika
jest aby dowolna z jego macierzy charakterystycznych była nieosobliwa, a
wszystkie jej elementy były różne od zera. Macierze Y , Z oraz H , G są
parami macierzami odwrotnymi:
Z·= Y-1 ; G = H-1
(11.19)
Czwórnik nazywamy nieprawidłowym (zdegenerowanym), jeśli posiada nie więcej niż pięć i nie mniej niż dwie macierze charakterystyczne.
Czwórnik, który posiada wyłącznie jedną macierz nazywamy zerowym.
dr inż. Marek Szulim
e-mail: [email protected]
14 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
Czwórnik bilateralny, unilateralny i nielateralny
Ze względu na zdolność do przesyłania sygnałów w obu lub jednym
kierunku, czwórnik nazywamy:
¾ BILATERALNYM
– jeśli posiada obydwie macierze łańcuchowe ( A i B ) - co oznacza możliwość przesyłania sygnałów w obie strony.
¾ UNILATERALNYM – jeśli posiada tylko jedną macierz łańcuchową ( A lub B ):
• gdy istnieje tylko macierz A – to
czwórnik ma zdolność przesyłania sygnałów od zacisków pierwotnych do
wtórnych;
• gdy istnieje tylko macierz B – to
czwórnik ma zdolność przesyłania sygnałów od zacisków wtórnych do pierwotnych.
¾ NIELATERALNYM
– jeśli nie posiada żadnej macierzy łańcuchowej - co oznacza niezdolność do przesyłania sygnałów.
Czwórnik odwracalny i nieodwracalny
Czwórnik, który spełnia zasadę wzajemności nazywamy czwórnikiem
ODWRACALNYM lub inaczej ENERGETYCZNIE SYMETRYCZNYM.
Zgodnie z zasadą wzajemności warunki odwracalności czwórnika można
wyrazić za pomocą elementów macierzy charakterystycznych:
Macierz
Y
Z
A
Czwórnik
odwracalny
y12= y21
z12= z21
det A=1
B
H
G
det B=1 h12= - h21 g12= - g21
Czwórnik, który nie spełnia zasady wzajemności jest czwórnikiem
nieodwracalnym.
dr inż. Marek Szulim
e-mail: [email protected]
15 /16
OBWODY I SYGNAŁY 1
Wykład 11 : Czwórniki – klasyfikacja, równania
Czwórnik symetryczny i niesymetryczny
Czwórnik, który spełnia zasadę wzajemności
a ponadto
zamiana miejscami wrót wejściowych z wyjściowymi tego
czwórnika nie powoduje żadnych zmian wielkości elektrycznych zaciskowych,
nazywamy
CZWÓRNIKIEM SYMETRYCZNYM
lub inaczej
IMPEDANCYJNIE SYMETRYCZNYM.
Konsekwencją symetryczności czwórnika są szczególne własności jego macierzy charakterystycznych:
Y
Z
A
z12= z21
det A=1
det B=1 h12= - h21 g12= - g21
y11= y22 z11= z22
a11= a22
b11= b22
Macierz
Czwórnik
y12= y21
symetryczny
B
H
G
det H=1 det G=1
UWAGA: nie każdy czwórnik odwracalny jest symetryczny - warunkiem koniecznym
symetryczności czwórnika jest jego odwracalność.
dr inż. Marek Szulim
e-mail: [email protected]
16 /16