Czwórniki i filtry

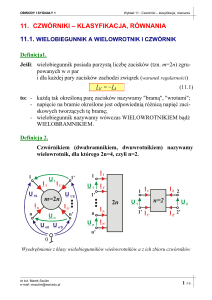
Czwórniki i filtry
Wykonał: Tomasz Szopa (kl. 4aE)
Czwórniki
Czwórnikiem (dwukrotnikiem) nazywamy układ mający cztery zaciski, a ściśle
dwie pary uporządkowanych zacisków.
Symbol graficzny
czwórnika w postaci
tzw. „czarnej skrzynki”
Dla czwórnika musi być spełniony warunek
I1=I`1 ; I2=I`2 ;
Jedną parę zacisków nazywamy wejściem, a drugą - wyjściem. Przeważnie do
wejścia jest doprowadzone źródło energii, a na wyjściu jest dołączony element
odbiorczy.
Klasyfikacja czwórników
Jeżeli wszystkie elementy wchodzące w skład struktury czwórnika są
liniowe, to taki czwórnik nazywamy czwórnikiem liniowym. Jeżeli czwórnik
zawiera chociaż jeden element nieliniowy, zaliczamy go do klasy czwórników
nieliniowych.
Czwórnik nazywamy symetrycznym, jeżeli po zamianie miejscami wejścia z
wyjściem nie zmieni się rozpływ prądów i rozkład napięć w obwodzie poza
czwórnikiem, tzn. w obwodzie dołączonym do wej. I w obwodzie dołączonym do
wyj.
Czwórniki dzielimy na odwracalne i nieodwracalne. Jeżeli do zacisków
wej. czwórnika odwracalnego doprowadzimy idealne źródło napięcia E, które w
zwartym obwodzie wyjścia wywoła przepływ prądu I, to po przeniesieniu tego
źródła do wyjścia, w zwartym obwodzie wejścia też popłynie prąd. Czwórnik, dla
którego spełniony będzie podany warunek, zwany warunkiem odwracalności,
nazywamy czwórnikiem odwracalnym.
Czwórniki dzielimy na pasywne i aktywne. Czwórnik nazywamy
pasywnym, jeżeli całkowita energia pobrana przez elementy czwórnika po
dołączeniu do jego zacisków źródła energii, jest nieujemna, tzn. dodatnia lub równa
zeru. Do chwili dołączenia źródła do zacisków czwórnika pasywnego prąd w nim
płynie. Czwórnik pasywny jest zbudowany np. z rezystorów, cewek i
kondensatorów. Czwórnik, który nie spełnia warunków określonych w podanej
definicji nazywamy czwórnikiem aktywnym. Czwórnik aktywny charakteryzuje się
tym, że w jego schemacie zastępczym występuje źródło, sterowane lub
niesterowane.
Równania czwórników
Równania czwórników określają związki między prądami i napięciami
na wej. I wyj. czwórnika. Są to dwa równania liniowe mające
współczynniki uzależnione od parametrów czwórnika. Związki między
napięciami i prądami można ustalić za pomocą metody klasycznej
wynikającej z obu praw Kirchhoffa, metody oczkowej lub węzłowej.
Wyróżniamy sześć postaci równań czwórnika:
1.
2.
3.
4.
5.
6.
Impedancyjną
Admitancyjną
Łańcuchowa prostą
Łańcuchową odwrotną
Hybrydową (mieszaną)
Hybrydową odwrotną
Do opisu czwórników pasywnych najczęściej stosuje się postać
łańcuchową. Opisując czwórniki aktywne, zwłaszcza formułując
równania tranzystora, korzysta się z postaci hybrydowej.
Parametry wchodzące do którejkolwiek z wymienionych postaci równań
czwórnika wyznacza się na podstawie znajomości struktury czwórnika i
wartości impedancji lub admitancji gałęzi tworzących tę strukturę.
Schematy zastępcze czwórników
Czwórniki, jako schematy zastępcze wielu urządzeń, można prawie
zawsze przedstawić za pomocą trzech impedancji tworzących strukturę
taką jak widać na rysunku niżej.
Na rysunku po lewej znajduje się czwórnik typu T, natomiast po prawej
czwórnik typu PI. Pierwszy z tych czwórników jest też nazywany
czwórnikiem gwiazdowym, gdyż jego gałęzie tworzą gwiazdę, a drugi
jest nazywany czwórnikiem trójkątowym, gdyż połączenie elementów
odpowiada połączeniu w trójkąt. W praktyce czwórniki o bardziej
złożonej strukturze, można dzięki stosowaniu reguł przekształcania
doprowadzić do jednej z podanych struktur.
Stany pracy czwórnika
Do zacisków wejściowych czwórnika 1-1` przeważnie jest doprowadzone
źródło. Zaciski wyjściowe 2 - 2` mogą być rozwarte i wtedy stan pracy
nazywamy stanem jałowym, mogą być zwarte, czyli połączone
bezimpedancyjnie i taki stan pracy nazywamy stanem zwarcia, i wreszcie
po dołączeniu do zacisków wyjściowych pewnej impedancji ZO , czwórnik
znajduje się w stanie obciążenia.
W stanie jałowym impedancja odbiornika jest równa nieskończoności,
wobec tego prądu I2 nie płynie, jest równy zeru. W stanie zwarcia
impedancja odbiornika jest równa zeru, zatem napięcie U2 jest równe zeru.
Impedancja wejściowa czwórnika
Stosunek napięcia na wejściu czwórnika do prądu na jego wejściu
nazywamy impedancją wejściową czwórnika. W zależności od stanu pracy
czwórnika możemy wyznaczyć impedancję wejściową czwórnika w stanie
obciążenia, w stanie jałowym i stanie zwarcia.
Połączenia czwórników.
Rozróżniamy trzy podstawowe układy połączeń czwórników:
1. Kaskadowe – zwane też łańcuchowym,
2. Równoległe,
3. Szeregowe.
Połączeniem kaskadowym czwórników nazywamy takie połączenie, przy
którym zaciski wyjściowe pierwszego czwórnika są przyłączone do zacisków
wejściowych drugiego czwórnika.
–I2`= I1``
I1 = I1`
U 1 = U 1`
[a1]
U2` =U1``
[a] = [a1] × [a2]
–I2`` = –I2
[a2]
U2`` = U2
Połączeniem równoległym (lewa strona rysunku) czwórników nazywamy takie
połączenie, przy którym zaciski wejściowe pierwszego czwórnika są połączone
z zaciskami wejściowymi drugiego czwórnika, jak również zaciski wyjściowe
pierwszego czwórnika są połączone z zaciskami wyjściowymi drugiego
czwórnika.
[y1]
[y2]
U1 = U1`= U1``
U2 = U2`= U2``
I1 = I1`+ I1``
I2 = I2`+ I2``
[y] = [y1] + [y2]
[z1]
[z2]
U1 = U1`+ U1``
U2 = U2`+ U2``
I1 = I1`= I1``
I2 = I2`= I2``
[z] = [z1] + [z2]
Polaczeniem szeregowym (prawa strona rysunku) dwóch czwórników
nazywamy takie polaczenie, przy którym zacisk 1` pierwszego czwórnika jest
połączony z zaciskiem 1 drugiego czwórnika, jak również zacisk 2` pierwszego
czwórnika jest połączony z zaciskiem 2 drugiego czwórnika.
Filtry
Filtrem nazywamy układ o strukturze czwórnika, który przepuszcza bez
tłumienia lub z małym tłumieniem napięcia i prądy o określonym paśmie
częstotliwości, a tłumi napięcia i prądy leżące poza tym pasmem.
Pasmo częstotliwości, które filtr przepuszcza bez tłumienia nazywamy
pasmem przepustowym, a pasmo częstotliwości, które filtr tłumi nazywamy
pasmem tłumieniowym. Częstotliwość, która oddziela pasmo przepustowe
od pasma tłumieniowego nazywamy częstotliwością graniczną filtra.
Podział filtrów
Ze względu na przeznaczenie filtry można podzielić na cztery podstawowe rodzaje:
•
dolnoprzepustowe
•
górnoprzepustowe
•
środkowoprzepustowe
•
środkowozaporowe
Ze względu na konstrukcję i rodzaj działania filtry można podzielić na:
• pasywne – nie zawierają elementów dostarczających energii do obwodu drgającego,
zawierają tylko elementy RLC
– jednostopniowe
– wielostopniowe
• aktywne – zawierają zarówno elementy RLC, jak również i elementy dostarczające
energię do filtrowanego układu np. wzmacniacze, układy nieliniowe.
Filtry można również podzielić na typy obwodów w jakich są używane:
• analogowe
• cyfrowe
Każdy z tych układów ma inne zastosowanie i w związku z tym inną konstrukcję.
Realizacje układowe filtrów mogą być bardzo różne, od prostych do bardzo
złożonych, wykorzystujących tylko elementy bierne (cewki, kondensatory i
rezystory) lub aktywne (uzupełnione o wzmacniacze).
Parametry filtrów
Dziedzina częstotliwości:
Charakterystyka amplitudowa- zależność wzmocnienia od częstotliwości; na
rysunku przedstawiona jest charakterystyka amplitudowa filtru
dolnoprzepustowego.
Pasmo przepustowe - zakres częstotliwości sygnałów przechodzących przez filtr
bez znacznego tłumienia. Najczęściej przyjmuje się, że krańcem pasma
przepustowego jest częstotliwość, dla której wzmocnienie filtru maleje o 3dB. Są
jednak filtry (o charakterystyce "równomiernie falistej") o nieco inaczej
zdefiniowanej częstotliwości krańcowej pasma przepustowego. Charakterystyka
amplitudowa filtru może nie być płaska, czyli może być nierównomierna (falista)
w obrębie pasma przepustowego. Definiuje się więc nierównomierność
charakterystyki w paśmie przepustowym, jak pokazano na rysunku.
Częstotliwość graniczna - częstotliwość krańcowa pasma przepustowego.
Sygnały o częstotliwościach z pasma zaporowego są znacząco tłumione przez filtr.
Początek pasma zaporowego definiuje się przez przyjęcie pewnej minimalnej
wartości tłumienia sygnałów. może to być na przykład 40dB.
Charakterystyka fazowa - zależność przesunięcia fazy sygnału wejściowego
filtru względem sygnału doprowadzonego do jego wejścia od częstotliwości tych
sygnałów. Przedmiotem zainteresowania jest zespolona charakterystyka
częstotliwościowa filtru, oznaczana zwykle symbolem H(s), s=jw, gdzie H, s i w są
liczbami zespolonymi. Ważność charakterystyki fazowej filtru wynika z faktu, że
jeśli składowe sygnału wyjściowego, których częstotliwości całkowicie mieszczą
się w paśmie przepustowym filtru, są różnie opóźnione po przejściu przez filtr, to
sygnał wyjściowy filtru będzie zniekształcony. Stałość czasu opóźnienia sygnałów
o rożnych częstotliwościach odpowiada liniowemu narastaniu przesunięcia fazy w
funkcji częstotliwości.
Stąd termin filtr o liniowym przesunięciu fazy odnosi się do filtru o idealnej
charakterystyce fazowej. Na rysunkach przedstawione są wykresy przesunięcia
fazy oraz czasu opóźnienia w funkcji częstotliwości dla filtru dolnoprzepustowego,
który jak widać nie jest filtrem o liniowym przesunięciu fazy. Charakterystyki
fazowe najlepiej jest rysować dla liniowo wyskalowanej osi częstotliwości.
Dziedzina czasu:
Podobnie jak wszystkie układy zmiennoprądowe, również filtry można
charakteryzować parametrami w dziedzinie czasu: czasem narastania, amplitudą
pierwszej oscylacji (przerzutem), czasem ustalania się odpowiedzi na wejściowy
skok napięcia. Znajomość tych parametrów jest szczególnie ważna wtedy, gdy
sygnałami wejściowymi filtru są skoki lub impulsy. Na poniższym rysunku
przedstawiona jest typowa odpowiedź filtru na wejściowy sygnał skoku
Czas narastania - czas upływający między chwilą pojawienia się skoku na
wejściu a chwilą, w której odpowiedź układu osiągnie 90% wartości stanu
ustalonego.
Czas ustalania - czas upływający do chwili, gdy odpowiedź znajduje się w
uprzednio zdefiniowanym obszarze wokół wartości ustalonej i więcej poza granice
tego obszaru nie wyjdzie.
Oscylacje, amplituda pierwszej oscylacji - są to pojęcia nie wymagające
specjalnych wyjaśnień. Występowanie oscylacji jest niepożądaną cechą
odpowiedzi filtru.
Źródła:
Internet:
•
•
•
•
•
•
•
•
•
http://www.mival.friko.pl/Pomiar_impedancji_czwornika.html
http://www.elektrotechnika.po.opole.pl/cwiczenia/czworniki/czworniki.
html
http://pl.wikipedia.org/wiki/Czw%C3%B3rnik_%28elektryka%29
http://pl.wikipedia.org/wiki/Filtr_%28elektronika%29
http://klimkiewicz.zs37.waw.pl/cwiczenie5.doc
http://www.kmg.ps.pl/to/podstawy_teorii_czwornikow/czworniki.html
http://www.kmg.ps.pl/to/filtry_ak/
http://www.stareradia.pl/theory/filters.html
http://www.elportal.pl/ea/filtry.html
Literatura:
•
Stanisław Bolkowski „Elektrotechnika” WSiP– wydanie ósme;
Warszawa 1998
Koniec