KARTA PRZEDMIOTU (SYLLABUS)

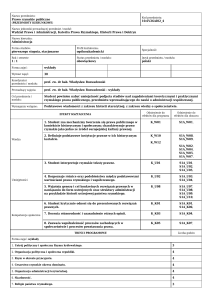
KARTA PRZEDMIOTU (SYLLABUS)
Kod przedmiotu
Wersja
przedmiotu
Podstawy matematyki finansowej
Nazwa
przedmiotu
Fundamentals of Financial Mathematics
Rok
akademicki
pierwsza
2012/2013
Wydział
Kierunek
Specjalność
Specjalizacja/kier.
dyplomowania
Poziom
kształcenia
(studiów)
Forma
prowadzenia
studiów
Przynależność do
grupy
przedmiotów
Poziom
przedmiotu
Formy zajęć
dydaktycznych,
wymiar , punkty
ECTS *
Kryterium doboru
słuchaczy
Język wykładowy
Forma nauczania
Jednostka
prowadząca
przedmiot
Koordynator
przedmiotu
dowolny
Wszystkie
Wszystkie
Studia I stopnia
Profil
kształcenia
(studiów)
Studia niestacjonarne
II lub III
Przedmiot ogólnouczelniany (HES)
Poziom podstawowy
Status przedmiotu
Wykład
12 h
Przedmiot wybieralny
….2 ECTS
*
Ćwiczenia
[h]
…. ECTS
…..
[h]
…. ECTS
Swobodny wybór studentów, zalecana jedynie znajomość elementów
matematyki na poziomie szkoły średniej
Polski
Wykład problemowy z elementami prezentacji multimedialnej
Wydział Ekonomiczny; Katedra Metod Ilościowych
Dr Zbigniew Śleszyński
Osoby prowadzące
przedmiot
Dr Zbigniew Śleszyński
Limit liczby
studentów
50
Adres strona
internetowa
Adres e-mail i
telefon
koordynatora
Semestr/semestry
[email protected]; tel 48 361 74 63
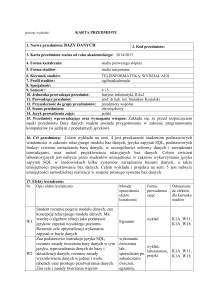
EFEKTY KSZTAŁCENIA I SPOSÓB PROWADZENIA ZAJĘĆ
.2.ECTS
*
Cel przedmiotu
Celem przedmiotu jest zapoznanie słuchaczy z podstawami zasad rachunku wartości pieniądza w
czasie. Przedmiot ma charakter elementarny, większość zagadnień prezentowana będzie na
podstawie prostych „przykładów z życia”. Każdy z nas posługuje się pieniądzem. Wykład ma za
zadanie sprawić, że będziemy robili to świadomi konsekwencji naszych decyzji.
Opis efektów kształcenia dla przedmiotu
numer
efektu
kształcenia
Student, który zaliczył przedmiot
(W) wie/(U) umie/(K) potrafi:
1.
Ma podstawową wiedzę z zakresu ustalania wartości
pieniądza w czasie
2.
Rozumie istotę ustalania wartości przyszłej i aktualnej
lokat, wkładów, rent
3.
SYMBOL
EKK
SYMBOL
EKO
K1A_W01,
K1A_W08
S1A_W01,
S1A_W06
K1A_W08,
K1A_W15
K1A_W12,
K1A_W15
Zna zasady budowy planu spłaty kredytów
4.
potrafi właściwie wyznaczyć wartość przyszłą lokat przy
różnych rodzajach kapitalizacji
5.
potrafi wyznaczyć wartość przyszłą i aktualną wkładów,
rent zgodnych i niezgodnych
6.
potrafi wykorzystać arkusz kalkulacyjny do prostych
obliczeń finansowych
K1A_U03
K1A_U03,
K1A_U04
Forma
realizacji
zajęć
dydaktycz
nych
wykład
Dyskusja,
praca końcowa
(domowa)
wykład
Dyskusja,
praca końcowa
(domowa)
S1A_W06,
S1A_W11
wykład
Dyskusja,
praca końcowa
(domowa)
S1A_U01,
S1A_U02
wykład
Dyskusja,
praca końcowa
(domowa)
wykład
Dyskusja,
praca końcowa
(domowa)
wykład
Dyskusja,
praca końcowa
(domowa)
wykład
Dyskusja,
praca końcowa
(domowa)
wykład
Dyskusja,
praca końcowa
(domowa)
wykład
Dyskusja,
praca końcowa
(domowa)
wykład
Dyskusja,
praca końcowa
(domowa)
S1A_W06
S1A_U02,
S1A_U07
S1A_U02
K1A_U12
S1A_U03
7.
8.
umie zbudować i zinterpretować plan spłaty kredytu
zna ograniczenia własnej wiedzy z zakresu wartości
pieniądza w czasie i rozumie potrzebę dalszego
kształcenia
9.
rozumie potrzebę intuicyjnego wyjaśnienia
rachunku wartości pieniądza w czasie
10.
rozumie korzyści z zastosowania matematyki finansowej
w życiu codziennym
K1A_U10
K1A_K01
S1A_K01
zasad
K1A_K03
K1A_K04,
K1A_K09
Metody
weryfikacji
efektów
kształcenia
(forma
zaliczeń)
S1A_K03
S1A_K07
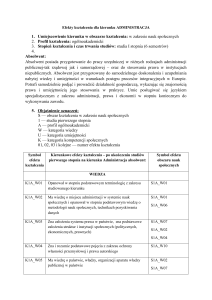
Macierz efektów kształcenia dla przedmiotu w odniesieniu do form realizacji zajęć
1.
inne
(dyskusja)...
Zajęcia
praktyczne
Pracownia
artystyczna
Konwersatorium
(W) wie/(U) umie/(K) potrafi:
Ćw. projektowe
Student, który zaliczył przedmiot
Ćw.
laboratoryjne
numer
efektu
kształce
nia
Wykład
Ćw.
audytoryjne
Forma realizacji zajęć dydaktycznych
Ma podstawową wiedzę z zakresu ustalania wartości
pieniądza w czasie
Rozumie istotę ustalania wartości przyszłej i aktualnej lokat,
wkładów, rent
X
3.
Zna zasady budowy planu spłaty kredytów
X
4.
potrafi właściwie wyznaczyć wartość przyszłą lokat przy
różnych rodzajach kapitalizacji
X
5.
potrafi wyznaczyć wartość przyszłą i aktualną wkładów, rent
zgodnych i niezgodnych
X
6.
potrafi wykorzystać arkusz kalkulacyjny do prostych obliczeń
finansowych
X
7.
umie zbudować i zinterpretować plan spłaty kredytu
X
8.
zna ograniczenia własnej wiedzy z zakresu wartości
pieniądza w czasie i rozumie potrzebę dalszego kształcenia
X
x
9.
rozumie potrzebę intuicyjnego wyjaśnienia zasad rachunku
wartości pieniądza w czasie
X
x
10.
rozumie korzyści z zastosowania matematyki finansowej w
życiu codziennym
X
x
2.
X
x
Treści kształcenia dla każdej formy zajęć dydaktycznych
Wykład:
Cele i zadania dyskretnej matematyki finansowej, podstawowe problemy praktyczne, przypomnienie
elementarnych informacji z matematyki (ciąg liczbowy, zbieżność, dwumian Newtona, liczba e, ciąg
arytmetyczny i geometryczny)
kapitalizacja odsetek i jej rodzaje.
Oprocentowanie lokat, kapitalizacja prosta, kapitalizacja złożona zgodna z góry i z dołu, kapitalizacja w
podokresach, kapitalizacja ciągła, równoważność oprocentowania, efektywna stopa procentowa,
kapitalizacja przy zmiennej stopie procentowej, analiza przykładów.
Oprocentowanie wkładów oszczędnościowych, wyznaczanie przyszłej wartości wkładów, wpłaty
jednakowej wielkości z dołu i z góry, ich bieżąca wartość,, wkłady niezgodne, wkłady częstsze niż
kapitalizacja z dołu i z góry,, wkłady gdy kapitalizacja jest częstsza niż wpłaty.
Zwrot długów i kredytów, zasady, różne formy spłaty, oprocentowanie efektywne, oprocentowanie a
inflacja, leasing.
Informacje o zasadach udzielania kredytów konsumenckich
Rachunek rent, renta z dołu, z góry, różne rodzaje wypłat, fundusze emerytalne.
System emerytalny w Polsce a rachunek rent
Informacje o zastosowaniach matematyki finansowej w analizie wybranych instrumentów finansowych
Sposób obliczania oceny końcowej
Na ocenę końcową mają wpływ następujące czynniki:
1. Obecność na wykładach (0-12 punktów)
2. Udział w dyskusji w trakcie wykładów (0-10 punktów)
3. Ocena samodzielnej pracy domowej (0-33 punkty)
Ocena końcowa: 0-27 pkt (nast.); 28-35 pkt (dst); 36-40 pkt (dst+); 41-45 pkt (db); 46-50 pkt db+;
51-55 pkt (bdb).
Literatura podstawowa i uzupełniająca; pomoce naukowe
Literatura podstawowa:
M Dobija, Cz. Smaga, Podstawy matematyki finansowej i ubezpieczeniowej, PWN, Warszawa 1995.
M. Dynus, P. Prewysz-Kwinto, Matematyka finansowa, TNOiK, Toruń 2005.
K. Piasecki, W. Ronka – Chmielowiec, Matematyka finansowa, Wydawnictwo C.H. BECK, Warszawa 2011
M. Podgórska, J. Klimkowska, Matematyka finansowa, PWN, Warszawa 2005.
M. Rutkowski (red), Matematyka finansowa, instrumenty pochodne, WNT, Warszawa 2003.
M. Sobczyk, Matematyka finansowa, AW Placet, Warszawa 2003.
Światłowski, M. Matłoka, Matematyka finansowa i funkcje arkusza kalkulacyjnego, WSB Poznań 2003.
Z. Śleszyński, Wybrane zagadnienia z matematyki finansowej, Wydawnictwo Politechniki Radomskiej,
Radom 2012.
Literatura uzupełniająca:
W. Bijak, M. Podgórska, J. Utkin, Matematyka finansowa, Bizant, Warszawa 1994.
I. Foltynowicz, Matematyka finansowa w Excelu, Ćwiczenia z..., Mikom, Warszawa 2001.
K Jajuga, T Jajuga, Inwestycje, instrumenty finansowe, ryzyko finansowe, inżynieria finansowa, PWN,
Warszawa 2004.
M. Kolupa , Metody matematyczne dla bankowców, Poltext, Warszawa 1992.
E. Nowak, M. Sobczyk, Rachunek wartości pieniądza w czasie, Wyd. UMCS, Lublin 1995.
K. Piasecki, Modele matematyki finansowej, Wydawnictwo Naukowe PWN, Warszawa 2007.
Nakład pracy studenta - bilans punktów ECTS
Udział w zajęciach, aktywność
Obciążenie studenta [h]
Wykład
12
Analiza treści wykładu, literatury
24
Opracowanie pracy zaliczeniowej
8
Sumaryczne obciążenie pracą studenta
Punkty ECTS za przedmiot
Informacje dodatkowe
Terminy odbywania
zajęć
Miejsce odbywania zajęć
Uwagi
44
2