Document

Zestaw zadań powtórzeniowych po klasie II LO
1. Rozwiąż równania i nierówności:
2
a. x  5 x  6  0
2
f. x  9  0
2
g. 2 x  6 x  0
1
 x 2  4 x  10  0
h. 2
2
b. x  4 x  4  0
2
c. 5 x  3x  0
2
d. 3x  8 x  4
e. 2x  3x  1  3xx  1  0
2
i. 3 x  8 x  3
2
2. Wykres funkcji y  2x przesunięto o 3 jednostki w lewo i 2 jednostki do góry. Zapisz wzór
funkcji, której wykres otrzymano.
3. Zbiorem rozwiązań nierówności x  2x  5  0 jest:
(,  2  5,)
(, 2  5,)
c.
d.
2
 10,20
4. Znajdź najmniejszą i największą wartość funkcji y   x  6 x  7 w przedziale
.
2
5. Wyznacz wartość funkcji f ( x)   x  3x  2 dla argumentu x  3  2.
a.
(,  5   2,)
b.
(,  5  2,)
6. Dana jest funkcja f ( x)  x  5  9. Wyznacz miejsce zerowe tej funkcji. Podaj, o ile
istnieją, wartość najmniejszą i największą tej funkcji.
2
7. Największą wartością funkcji kwadratowej f ( x)  2x  3  4 jest:
2
a. 3
b. -2
c. -4
d. 4
1
g ( x )  x 2  2.
2
8. Dane są funkcje: f ( x)  2 x  2,
a. Znajdź miejsca zerowe funkcji k ( x)  f ( x)  g ( x).
b. Wyznacz wartość k (3).
c. Dla jakich argumentów wartości funkcji f są większe od wartości funkcji g?
d. Narysuj wykres funkcji h( x)  g ( x  3)  2.
2
9. Dane są funkcje: f ( x)  2 x  1, h( x)   x  2 x  1.
a. Naszkicuj wykresy obu funkcji.
b. Oblicz współrzędne punktów wspólnych tych wykresów.
10. Funkcja kwadratowa f osiąga wartość najmniejszą równą (-4) dla argumentu 6, a liczba 2 jest
miejscem zerowym funkcji f. Wykres funkcji liniowej g jest prostopadły do prostej o równaniu
y  2 x  8 i przechodzi przez punkt A  (6,8).
a. Wyznacz wzór funkcji f w postaci kanonicznej oraz wzór funkcji g.
b. Oblicz współrzędne punktów wspólnych wykresów funkcji f i g.
11. Znajdź postać ogólną wzoru określającego funkcję kwadratową, wiedząc, że wierzchołek jej
wykresu ma współrzędne (-2,1), a jednym z jej miejsc zerowych jest liczba (-4).
12. Napisz w postaci kanonicznej i postaci ogólnej wzór funkcji kwadratowej, wiedząc, że do jej
wykresu należy punkt (1, 3) i że dla x=2 funkcja osiąga największą wartość y=4.
2
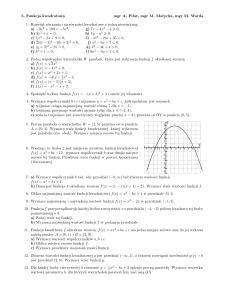
13. Znajdź współrzędne wierzchołka paraboli y  3x  3x  6 oraz punktów przecięcia tej
paraboli z osiami układu współrzędnych. Narysuj tę parabolę i podaj przedziały monotoniczności.
14. Dla jakich argumentów wartości funkcji y  x  32 x  5 są mniejsze od wartości funkcji
y  4 x 2  2 x  20 ?
15. Przedstaw liczbę 68 w postaci sumy dwóch liczb tak, aby suma kwadratów tych liczb była
najmniejsza.
16. Funkcja kwadratowa o miejscach zerowych x1  3, x2  4, której wykres przechodzi przez
punkt P=(0,12) ma wzór:
Zebrała: Iwona Kowalik
1
Zestaw zadań powtórzeniowych po klasie II LO
a. f ( x)  2x  3x  4
c. f ( x)  x  3x  4
b. f ( x)  x  3x  4
d. f ( x)  x  3x  4
2
17. Zbiorem rozwiązań nierówności x  6  0 jest:
x   6, 6
x   3,3
a.
b. x   , 6  6 ,  c.
d. x  (6,6)
18. Suma kwadratów trzech kolejnych liczb naturalnych wynosi 149. Wyznacz te liczby.
2
2
19. Dany jest okrąg o równaniu x  5   y  1  25. Długość tego okręgu jest równa:

 
b. 10
a. 25

d. 2
c. 6
20. Wskaż równanie okręgu o środku w punkcie S=(-1, 2) i promieniu r  2 :
2
2
2
2
a. x  1   y  2  2
b. x  1   y  2  2
d. x  1   y  2  2
3
2
2
3
2
21. Dane są wielomiany: W ( x)  x  ax  3x  1, F ( x)  2 x  bx  4, H ( x)  x  7 x  8 x  c.
Wyznacz współczynniki a, b, c tak, aby W ( x)  F ( x)  H ( x).
c. x  1   y  2  2
2
2
2
2
2
3
22. Dane są wielomiany W ( x)  3x  2 x  5 oraz P( x)  2 x  2 x  5. Wielomian W ( x)  P( x)
jest równy:
3
2
3
2
3
2
3
2
a. 2 x  3x
b. 2 x  3x
c.  2 x  3x
d.  2 x  3x
3
2
23. Dany jest wielomian W ( x)  x  kx  4.
a. Wyznacz współczynnik k tego wielomianu, wiedząc, że wielomian ten jest podzielny
przez dwumian x+2.
b. Dla wyznaczonej wartości k rozłóż wielomian na czynniki i wyznacz wszystkie jego
pierwiastki.
2
24. Wielomian W ( x)  x x  2  x  2 można zapisać w postaci:


2
b. W ( x)  x  1 x  2
d. W ( x)  x  1x  1x  2
2
a. W ( x)  x ( x  2)
2
c. W ( x)  x x  2 
3x  5
1

A  x  R : x 3  2x 2  x  2  0 , B  x  R :
  ,
2
2  C- zbiór liczb

25. Dane są zbiory:
całkowitych większych od -4. Wyznacz zbiory: A  B, A  C , A \ B.


3
2
26. Dany jest wielomian W ( x)  x  2 x  x  m. Liczba 1 jest jednym z pierwiastków tego
wielomianu. Znajdź najmniejszy pierwiastek wielomianu W(x).
27. Rozłóż na czynniki wielomiany:
3
4
3
2
a. 2 x  16
d. 3x  9 x  30 x
4
3
2
b. 2 x  4 x  6 x
3
2
c. 3x  4 x  9 x  12
28. Rozwiąż równania:
4
3
2
a. x  4 x  4 x  0
3
b. x  13x  12  0
3
2
c. x  x  x  1  0
29. Rozwiąż nierówności:
2
a. 5  x  x  6 x  5  0


3
2
b. x  5 x  x  5  0
3
2
e. 2 x  3x  10 x  15
3
d. 2 x  18 x  0
3
2
e. x  4 x  x  4  0
3
2
f. x  2 x  3x  6  0
3
2
c. 4 x  12 x  x  3  0
3
2
d. x  2 x  x  2  0
3
2
30. Do wykresu funkcji f ( x)  2 x  4 x  2 x  5 należy punkt o współrzędnych:
a. (-1, -9)
b. (-1, -5)
c. (-1, -10)
d. (-1, -13)
Zebrała: Iwona Kowalik
2
Zestaw zadań powtórzeniowych po klasie II LO
31. Ciąg a n  jest ciągiem arytmetycznym.
a. Zapisz wzór ogólny ciągu a n  , w którym a2  4, a8  1.
b. Wyznacz taką liczbę n wyrazów tego ciągu, aby sumy częściowe S n i S 2 n jego
wyrazów spełniały warunek S 2 n  S n  205.
n2
1
.
.
3n  1 Wyznacz wszystkie wyrazy tego ciągu większe od 2
32. Dany jest ciąg an , gdzie
33. W ciągu geometrycznym drugi wyraz jest równy (-2), a trzeci wyraz (-18). Iloraz tego ciągu jest
równy:
a. -9
b. -3
c. 3
d. 9
34. Piąty wyraz ciągu arytmetycznego jest równy 17, a różnica tego ciągu jest równa (-2). Drugi
wyraz tego ciągu jest równy:
a. 9
b. 11
c. 23
d. 25
35. Ciąg (a, b, c) jest arytmetyczny i a+b+c=33. Ciąg (a, b+3, c+13) jest geometryczny. Oblicz a, b i
c.
36. Zbadaj monotoniczność ciągu określonego wzorem:
1
a. a n  4n  1
an  1 
n
d.
a  2n 2  2
b. n
n 1
an 
2
an  3 
n3
e.
n
c.
an 
37. Ciąg arytmetyczny ma 10 wyrazów. Iloczyn pierwszego i ostatniego wyrazu ciągu wynosi 63.
Suma tych wyrazów jest równa 24. Znajdź pierwszy wyraz i różnicę tego ciągu.
38. W ciągu arytmetycznym a n  dane są wyrazy: a3  4, a6  19. Wyznacz wszystkie wartości n,
 
dla których wyrazy ciągu a n są mniejsze od 200.
1
1
a3  ; a6 
4
32. . Wyznacz S 7 .
39. Wyznacz ciąg geometryczny, mając dane
40. Oblicz długości boków i pole trójkąta prostokątnego o obwodzie 120cm, wiedząc, że długości
jego boków tworzą ciąg arytmetyczny.
41. Oblicz sumę wszystkich naturalnych liczb dwucyfrowych, które przy dzieleniu przez 6 dają
resztę 5.
42. Na konto, którego oprocentowanie wynosi 4% w skali roku, wpłacono 5000 zł. Oblicz jaki
będzie stan konta po upływie 3 lat, jeśli odsetki dopisywane są:
a. co rok
b. co pół roku
43. Dla jakiej wartości n liczby 3n  5,4n  12 i 11 są kolejnymi wyrazami ciągu arytmetycznego?
44. Sklep sprowadza z hurtowni kurtki, płacąc po 100 zł za sztukę, i sprzedaje średnio 40 sztuk
miesięcznie po 160 zł Zaobserwowano, że każda kolejna obniżka ceny sprzedaży kurtki o 1 zł
zwiększa sprzedaż miesięczną o 1 sztukę. Jaką cenę kurtki powinien ustalić sprzedawca, aby jego
miesięczny zysk był największy?
6
 3,
45. Niech A oznacza zbiór rozwiązań nierówności x
B - zbiór rozwiązań nierówności
4
3
2
A

B
,
A

B
,
A
\
B
,
B \ A.
x  5 x  4 x  0. Wyznacz zbiory:
46. Określ dziedzinę wyrażenia:
4x  2
a. 2 x  6
Zebrała: Iwona Kowalik
x3
d. x  4 x  5
2
3
Zestaw zadań powtórzeniowych po klasie II LO
4x
b. x  9
2x
2
c. 2 x  6 x  5
2
2x  3
e. 3x  1x  8
3x
x  5 x  6 jest:
47. Dziedziną funkcji
a. D  R \ 2 b. x  R
c. D  R \ 2,3
d. D  R \ 3
48. Oblicz długość promienia okręgu opisanego oraz promienia okręgu wpisanego w trójkąt
o bokach a-12, b=5, c=13.
49. W koło o promieniu 3dm został wpisany trójkąt o kącie
  40 o . Oblicz pole zamalowanej części koła.
f ( x) 
2
2
50. Pole trapezu równoramiennego jest równe 39 3cm . Ramię trapezu ma długość 6 3cm
i tworzy z dłuższą podstawą kąt 30o. Oblicz obwód trapezu.
51. Wysokość CD trójkąta równoramiennego ABC jest równa 8, a ramię AC ma długość 10.
Podstawa AB tego trójkąta ma długość:
a. 12
b. 6
c. 89
d. 2 41
52. W trapezie prostokątnym krótsza przekątna ma długość 8cm i tworzy z dłuższą podstawą kąt
30o. Różnica między długościami podstaw jest równa 4cm. Oblicz pole i obwód trapezu.
53. Jeden kątów czworokąta wpisanego w okrąg jest o 18o większy od kata sąsiedniego, który ma
miarę 37o. Jakie miary mają kąty tego czworokąta?
54. Na okręgu opisano trapez równoramienny o krótszej podstawie 6cm. Wiedząc, że obwód
trapezu wynosi 60cm, oblicz jego pole.
55. Wyznacz pole trójkąta równobocznego, którego wysokość jest o 1 cm krótsza od boku trójkąta.
56. Oblicz obwód i pole trapezu równoramiennego, jeżeli większa podstawa ma 16cm, ramię 6cm,
a kat ostry trapezu ma 50o.
57. Oblicz pole trójkąta równoramiennego o podstawie 16 i ramionach długości 17.
58. Znajdź współrzędne punktów przecięcia wykresów funkcji f i g, jeżeli:
3x  3; dlax  2
f ( x)  
2
 2 x  7, dlax  2 , g ( x)   x  6 x  11.
59. W prostokącie długości boków różnią się o 7cm. Oblicz pole tego prostokąta, jeśli jego
przekątna ma długość 13cm
60. W trapezie równoramiennym o obwodzie 22cm dłuższa podstawa jest o 5cm dłuższa od
ramienia, a krótsza podstawa jest o 3 cm krótsza od ramienia. Oblicz pole trapezu.
61. Pole rombu o boku długości 8cm wynosi 50cm2. Znajdź miary kątów tego rombu.
o
62. Pole trójkąta o bokach a  4cm, c  5cm oraz kącie   60 zawartym między danymi bokami
jest równe:
9
3cm 2
2
2
2
10
3
cm
2
a.
b. 10cm
d. 5 3cm
log 3 27  log 3 9
63. Liczba
jest równa:
243
a. 0
b.
c. 5
d. 18
Zebrała: Iwona Kowalik
4
Zestaw zadań powtórzeniowych po klasie II LO
64. Liczba log 36 jest równa:
a. 2 log 18
b. log 40  2 log 2
65. Liczba log 12 jest równa:
c. 2 log 4  3 log 2
d. 2 log 6  log 1
a. log 3  log 4
b. log 3  log 4
c. log 16  log 4
d. log 10  log 2
66. Liczba log 24 jest równa:
a. 2 log 2  log 20
b. log 6  2 log 2
c. 2 log 6  log 12
d. log 30  log 6
Zebrała: Iwona Kowalik
5