Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra

Politechnika Gdańska
Wydział Elektrotechniki i Automatyki
Katedra Inżynierii Systemów Sterowania
Struktury i Algorytmy Wspomagania Decyzji
Zadanie projektowe 2
Czas realizacji: 6 godzin
Maksymalna liczba punktów: 80
Opracowanie:
Kazimierz Duzinkiewicz, dr hab. inż.
Robert Piotrowski, dr inż.
Zadanie projektowe składa się z kilku Zagadnień. Należy rozwiązać wszystkie
Zagadnienia.
Zagadnienie 1 [30 pkt]
Dwóch absolwentów wyższej uczelni postanowiło wejść do branży komputerów
osobistych. Zdecydowali wytwarzać (faktycznie, po prostu montować - z części
zamawianych u innych dostawców) dwa typy komputerów: A oraz S. Przypuszcza
się, że będą mogli, w przewidywalnej przyszłości, sprzedać tak wiele komputerów,
jak tylko będą mogli wyprodukować. Jednakże chcą oni ustalić wielkość produkcji
tak, aby wykorzystywać nie więcej niż małą grupę pracowników produkcyjnych.
Bardziej szczegółowo, chcą oni utrzymać czas montowania w granicach 150 godzin
na tydzień i czas testowania w granicach 70 godzin tygodniowo. Komputer A
wymaga 4. godzin montowania i 3. godzin testowania a komputer S pochłania
odpowiednio 6 godzin i 2 godziny. Przewidywany zysk ze sprzedaży komputera A
wynosi 200 PLN na jednostkę a dla komputera S 450 PLN. Partnerzy chcą
maksymalizować zysk i maksymalizować ogólną liczbę jednostek produkowanych
każdego tygodnia (to znaczy tak, aby zostać zauważonym na rynku). W żadnym
wypadku nie zaakceptują wzrostu czasu montowania ponad 150 godzin i czasu
testowania ponad 70 godzin, gdyż wymagałoby to zatrudnienia dodatkowych
pracowników lub wykorzystywania nadgodzin przez już zatrudnionych w pełnym
wymiarze godzin pracowników.
Należy:
1. Sformułować matematyczną postać problemu i przedstawić go graficznie.
2. Korzystając z punktu 1, wskazać zbiór rozwiązań optymalnych w sensie Pareto.
3. Sformułować jednokryterialną reprezentację problemu przyjmując następujące
założenia:
 pojedynczym najważniejszym celem jest maksymalizacja zysku,
 liczby godzin montowania i godzin testowania nie mogą, w jakichkolwiek
warunkach, być przekroczone,
 w każdym tygodniu produkuje się co najmniej wskazaną liczbę sztuk
komputerów (dobrać odpowiednią wartość poziomu aspiracji, aby przestrzeń
decyzyjna nie była pusta).
2
Przedstawić graficzne rozwiązanie tego zadania i wyciągnąć wnioski. Czy
uzyskane rozwiązanie należy do zbioru rozwiązań optymalnych w sensie Pareto?
4. Sformułować jednokryterialną reprezentację problemu przyjmując następujące
założenia:
 pojedynczym najważniejszym celem jest maksymalizacja ogólnej liczby
komputerów produkowanych każdego tygodnia,
 liczby godzin montowania i godzin testowania nie mogą, w jakichkolwiek
warunkach, być przekroczone,
 uzyskuje się co najmniej wskazaną liczbę PLN całkowitego zysku ze
sprzedaży komputerów (dobrać odpowiednią wartość poziomu aspiracji, aby
przestrzeń decyzyjna nie była pusta).
Przedstawić graficzne rozwiązanie tego zadania i wyciągnąć wnioski. Czy
uzyskane rozwiązanie należy do zbioru rozwiązań optymalnych w sensie Pareto?
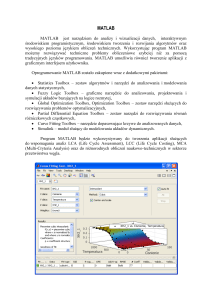
5. Rozwiązać punkty 3 i 4 w środowisku MATLAB, przy czym:
 zdefiniować zadanie optymalizacji (liniowe, nieliniowe, jednocelowe, z
ograniczeniami itp.),
 zaproponować funkcje do rozwiązania sformułowanego zadania (optimization
toolbox) i uzasadnić swój wybór,
 krótko opisać wybraną funkcję tzn. do jakiego rodzaju zadań optymalizacji
może być stosowana, jaka jest jej składnia,
 rozwiązać zadanie poprzez napisanie odpowiedniego m-pliku, który należy
dołączyć do sprawozdania.
6. Porównać wyniki uzyskane metodą graficzną i za pomocą programu MATLAB.
Zagadnienie 2 [30 pkt]
Mały zakład produkcyjny wytwarza dwa rodzaje produktów: A i B. Produkcję obu
produktów ograniczają operacje technologiczne 1, 2 i 3.
Podstawowymi celami firmy jest maksymalizacja zysku i maksymalizacja ogólnej
ilości produktów wytwarzanych w danym tygodniu. Zysk firmy na jednym produkcie
A wynosi 4 PLN, zaś na jednym produkcie B 2 PLN.
Ograniczenia na możliwości produkcyjne w zakresie operacji technologicznych 1, 2 i
3, w danym tygodniu przedstawia Tabela 1. Zadaniem operacji technologicznej 3 jest
3
łączenie ze sobą produkty A i B. W Tabeli 2 podano ilościowe udziały
poszczególnych operacji w ogólnej możliwości produkcyjnej.
Tabela 1. Możliwości produkcyjne
Operacja
Możliwości produkcyjne dla produktów A i B
Operacja technologiczna 1
70
Operacja technologiczna 2
168
Operacja technologiczna 3
190
Tabela 2. Ilościowe udziały
Operacja
Produkt A
Produkt B
Operacja technologiczna 1
6
4
Operacja technologiczna 2
4
12
Operacja technologiczna 3
18
7
Należy:
1. Sformułować matematyczną postać problemu i przedstawić ją graficznie w
przestrzeni decyzyjnej i przestrzeni celów.
2. Korzystając z punktu 1, wskazać zbiór rozwiązań optymalnych w sensie Pareto.
3. Sformułować jednokryterialną reprezentację problemu wykorzystując metodę
ograniczenia (wybierając jedną z funkcji celu).
4. Korzystając ze środowiska MATLAB, dla różnych wartości
 , znaleźć punkty
zbioru rozwiązań optymalnych w sensie Pareto (minimalna liczebność zbioru
wynosi 50). Zakwalifikować rozwiązywane w tym celu zadanie optymalizacji,
zaproponować funkcje do rozwiązania sformułowanego zadania i uzasadnić swój
wybór. Do sprawozdania dołączyć m-plik.
5. Otrzymany zbiór rozwiązań optymalnych w sensie Pareto przedstawić graficznie
w przestrzeni decyzji i przestrzeni celów.
6. Wyciągnąć wnioski odnośnie uzyskanych wyników i metody ograniczenia. Czym
będzie się różniło rozwiązanie, jeżeli w metodzie ograniczenia zostanie wybrana
druga funkcja celu?
4
Zagadnienie 3 [20 pkt]
Dwóch absolwentów wyższej uczelni postanowiło wejść do branży komputerów
osobistych. Zdecydowali wytwarzać (faktycznie, po prostu montować - z części
zamawianych u innych dostawców) dwa typy komputerów: A oraz S. Przypuszcza
się, że będą mogli, w przewidywalnej przyszłości, sprzedać tak wiele komputerów,
jak tylko będą mogli wyprodukować. Jednakże chcą oni ustalić wielkość produkcji
tak, aby wykorzystywać nie więcej niż małą grupę pracowników produkcyjnych.
Bardziej szczegółowo, chcą oni utrzymać czas montowania w granicach 150 godzin
na tydzień i czas testowania w granicach 70 godzin tygodniowo. Komputer A
wymaga 4. godzin montowania i 3. godzin testowania a komputer S pochłania
odpowiednio 6 godzin i 2 godziny. Dodatkowo po pewnych analizach stwierdzili, że
nie będą produkować więcej niż 20 sztuk komputerów typu A i nie więcej niż 23
sztuki komputera typu S. Przewidywany zysk ze sprzedaży komputera A wynosi 300
PLN na jednostkę a dla komputera S 450 PLN. Partnerzy chcą maksymalizować zysk
i maksymalizować ogólną liczbę jednostek produkowanych każdego tygodnia (to
znaczy tak, aby zostać zauważonym na rynku). W żadnym wypadku nie zaakceptują
wzrostu czasu montowania ponad 150 godzin i czasu testowania ponad 70 godzin,
gdyż wymagałoby to zatrudnienia dodatkowych pracowników lub wykorzystywania
nadgodzin przez już zatrudnionych w pełnym wymiarze godzin pracowników.
Należy:
1. Sformułować matematyczną postać problemu.
2. Sformułować jednokryterialną reprezentację problemu wykorzystując metodę
agregacji. Zaproponować wagi wykorzystując informacje zawarte w treści
zadania.
3. Korzystając ze środowiska MATLAB zbadać zależności pomiędzy wartościami
wag funkcji celu a wartościami funkcji celu. Przedstawić te zależności w postaci
graficznej. Należy pamiętać, aby każde otrzymane rozwiązanie bezwzględnie
spełniało warunki zadania. Jakie działania należy wykonać, aby rozwiązanie było
całkowitoliczbowe?
Zakwalifikować
rozwiązywane
zadanie
optymalizacji,
zaproponować funkcje do rozwiązania sformułowanego zadania i uzasadnić swój
wybór. Do sprawozdania dołączyć m-plik.
4. Wyciągnąć wnioski odnośnie uzyskanych wyników i metody agregacji.
5