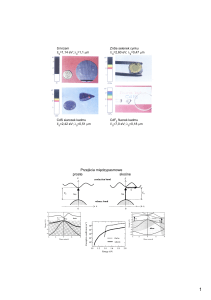
Półprzewodniki
Teoria złącza PN
Budowa i właściwości elektryczne ciał
stałych - wprowadzenie
Budowa atomu:
a) model starożytny
b) model J.J. Thompsona
c) model E. Rutherforda
d) model N. Bohra
e) wynikająca z mechaniki
falowej Schroedingera i
zasady nieozn.
Heisenberga
f) model wg. obecnego
stanu wiedzy
Budowa i właściwości elektryczne ciał
stałych - wprowadzenie
Model Bohra:
- postulat 1 – elektrony poruszają się po orbitach
- postulat 2 – elektrony poruszają się po określonych, stałych
orbitach, dla każdej obowiązuje równanie będące krotnością stałej
Plancka h:
mv 2πr = nh
Gdzie: m – masa, v – pradkość, r – promień n-tej orbity
- postulat 3 – orbita, dla której elektron ma mniejszą energię
nazywamy stacjonarną; „zastrzyk” energii dla elektronu – zmiana orbity
na dozwoloną (atom wzbudzony)!!!, po krótkim czasie powrót na orbitę
stacjonarną i wypromieniowanie energii ∆E o częstotliwości v:
∆E = hv
1
Budowa i właściwości elektryczne ciał
stałych - wprowadzenie
Ciała stałe:
- regularna, okresowa budowa atomowa
- okresowość występuje we wszystkich kierunkach
- tworzą sieć krystaliczną (silne wiązania – brak przemieszczania)
- dopuszczalny jedynie ruch cieplny wokół położenia równowagi
- elektrony walencyjne – słabsze wiązania z jądrem atomu ze
względu na drgania cieplne oraz siły wzajemnego oddziaływania
Wynik – elektrony swobodne (gaz elektronowy) poruszające
się w krysztale pod wpływem pola elektrycznego
Budowa i właściwości elektryczne ciał
stałych - wprowadzenie
Przewodnictwo elektryczne materiału:
- zależy od liczby elektronów swobodnych
- zależy od temperatury:
Przewodniki – wzrost temp. zmniejsza przewodnictwo –
większa energia drgań jonów (wzrost rezystancji)
Półprzewodniki – wzrost temp. zwiększa przewodnictwo –
więcej elektronów walencyjnych się uwalnia (wzrost
konduktywności)
Budowa i właściwości elektryczne ciał
stałych - wprowadzenie
Model pasmowy ciała stałego:
- atomy (elektrony) znajdują się w określonych stanach
energetycznych
- dozwolone stany (poziomy) energetyczne oddzielone są
strefami zabronionymi (przerwami energetycznymi)
- atom (elektron) może zmienić swoją energię tylko
skokowo
- wiąże się to z pobraniem/oddaniem przez atom energii
określonej przerwą energetyczną
2
Budowa i właściwości elektryczne ciał
stałych - wprowadzenie
Model energetyczny:
a) atomu: EP – energia w
stanie podstawowym,
EW – energia w stanie
wzbudzonym, ∆E –
pamo zabronione
(przerwa energetyczna)
b) ciała stałego
Budowa i właściwości elektryczne ciał
stałych - wprowadzenie
- Oba pasma: podstawowe i przewodnictwa obsadzone są
przez elektrony walencyjne.
- Pozostałe elektrony są silnie związane z atomem i
całkowicie wypełniają powłoki (orbity) w liczbie 2n2.
- Odłączenie ich od atomu powoduje jego zniszczenie!!!!!
- Wzajemne położenie pasm: podstawowego i
przewodnictwa oraz liczba elektronów walencyjnych
decydują o właściwościach elektrycznych ciała stałego.
Budowa i właściwości elektryczne ciał
stałych - dielektryki
Układ pasm energetycznych dielektryka
3
Budowa i właściwości elektryczne ciał
stałych - dielektryki
Podstawowe właściwości dielektryków:
- mała konduktywność 10-15 ... 10-12 S/m (1012...1015 Ωm)
- pasmo podstawowe całkowicie obsadzone przez elektrony
- brak elektronów swobodnych (walencyjnych)
- elektrony nie występują w paśmie przewodnictwa
- duża szerokość pasma zabronionego 10eV
- niemożność przejścia elektronu do pasma przewodnictwa
- pod wpływem wysokiego napięcia dielektryk ulega przebiciu i
zniszczeniu
Budowa i właściwości elektryczne ciał
stałych - przewodniki
Układ pasm energetycznych przewodnika
Budowa i właściwości elektryczne ciał
stałych - przewodniki
Podstawowe właściwości przewodników:
- duża konduktywność 106...109 S/m (mała rezystywność 10-9...10-6 Ωm)
- brak pasma zabronionego – pasma podstawowe i przewodnictwa
zachodzą na siebie
- w paśmie przewodnictwa znajduje się bardzo dużo elektronów
swobodnych
- przyłożenie niewielkiego napięcia powoduje przepływ prądu
- wzrost temperatury powoduje wzrost rezystancji
Najlepszymi przewodnikami są metale – ciała stałe o
budowie krystalicznej zawierające elektrony swobodne.
4
Budowa i właściwości elektryczne ciał
stałych - półprzewodniki
Układ pasm energetycznych półprzewodnika
Budowa i właściwości elektryczne ciał
stałych - półprzewodniki
Podstawowe właściwości półprzewodników:
- konduktywność 10-8...10-4 S/m (rezystywność 104...108 Ωm)
- przerwa energetyczna 0.1 – 2 eV
- w temperaturze pokojowej występują elektrony w paśmie
przewodnictwa
- wraz ze wzrostem temperatury rezystancja półprzewodnika maleje
- działając na półprzewodnik: ciepłem, promieniowaniem, polami
elektrycznym lub magnetycznym łatwo jest przenieść elektron z pasma
podstawowego do pasma przewodnictwa
Półprzewodniki - dziury i elektrony
Przejście pomiędzy
poziomami - generacja i
rekombinacja; pary dziura
elektron (garaż piętrowy).
Prąd w
półprzewodniku:
- elektronowy w paśmie
przewodnictwa w kierunku
elektrody dodatniej
- dziurowy w paśmie
podstawowym w kierunku
elektrody ujemnej
5
Półprzewodniki - dziury i elektrony
Ruchliwość dziur jest znacznie mniejsza od ruchliwości
elektronów.
O przewodności półprzewodnika decyduje liczba elektronów
i dziur.
Nośniki większościowe – decydujące o prądzie w
półprzewodniku (większy wkład w przepływ prądu).
Nośniki mniejszościowe – mające mniejszy wpływ na
przepływ prądu przez półprzewodnik.
W zależności od technologii wykonania nośnikami
większościowymi mogą być dziury lub elektrony.
Półprzewodniki samoistne
Samoistne – niedomieszkowane (koncentracja elektronów
= koncentracji dziur).
IV grupa układu okresowego:
- węgiel
- krzem
- german
- antymonek galu (GaSb)
- arsenek galu (GaAs)
- itd.
Półprzewodniki samoistne
6
Półprzewodniki domieszkowane
Wprowadzenie domieszki – zakłócenie atomowe sieci
krystalicznej – zwiększenie konduktywności.
Podstawowe pierwiastki gr. IV: german i krzem domieszkuje
się pierwiastkami z
- gr. III: B – borem, Al – glinem, Ga – galem, In - indem
- gr. V: P – fosforem, As – arsenem, Sb – antymonem, Bi bizmutem
Półprzewodniki domieszkowane
Rodzaje domieszek:
- donorowa (pierwiastkiem pięciowartościowym) – typ n
półprzewodnika
Półprzewodniki domieszkowane
Rodzaje domieszek:
- akceptorowa (pierwiastkiem trójwartościowym) – typ p półprzewodnika
7
Półprzewodniki – wpływ pola elektrycznego;
przewodzenie
Rezystancja:
R=
U
l
=ρ
I
S
gdzie: ρ – rezystywność materiału, l – długość, S – pole
przekroju poprzecznego
Konduktancja:
G=
S
1 I
= =σ
R U
l
gdzie: σ – rezystywność materiału,
Półprzewodniki – wpływ pola elektrycznego;
przewodzenie
Przekształcając:
I
J
S
σ= =
U E
l
Gęstość przepływu prądu przez powierzchnię:
J = qnv
gdzie: q – ładunek nośników (1.6⋅10-19 C dla elektronów lub
dziur), n – liczba nośników na m3, v – średnia prędkość
unoszenia
Półprzewodniki – wpływ pola elektrycznego;
przewodzenie
Stąd:
σ=
qnv
E
Wprowadzając ruchliwość ładunków w danym materiale
(różną dla dziur i elektronów!!!):
µ=
v
E
Otrzymujemy:
σ = qnµ n + qpµ p = q (nµ n + pµ p )
8
Półprzewodniki – wpływ pola elektrycznego;
przewodzenie
Dla silnie domieszkowanego donorami półprzewodnika
typu n:
σ n ≈ qµ n N d
Dla silnie domieszkowanego akceptorami półprzewodnika
typu p:
σ p ≈ qµ p N a
Dla półprzewodnika domieszkowanego zarówno
donorami i akceptorami:
σ = q Nd − Na µ
Przy czym µ zależy od typu półprzewodnika i jest równe µn
lub µp
Półprzewodniki – transport nośników
nadmiarowych
Prąd dyfuzji – prąd wywołany przez chaotyczny ruch
rozproszonych nośników nadmiarowych, z obszarów o
większej koncentracji do obszarów o mniejszej
koncentracji, w sieci krystalicznej półprzewodnika
(występuje oprócz rekombinacji)
Gęstość prądu dyf. elektronów:
J nD = qDn grad (n )
Gęstość prądu dyf. dziur:
J pD = − qD p grad ( p )
Dn, Dp – wspólczynniki dyfuzji
n,p – koncentracja elektronów/dziur w danym obszarze
półprzewodnika
Półprzewodniki – transport nośników
nadmiarowych
Prąd unoszenia (konwekcji) – prąd wywołany ruchem
ładunków elektrycznych, pod wpływem np. istniejącego pola
elektrycznego, nie związanych z cząstkami elementarnymi
ośrodka w którym się poruszają. Pole elektryczne wytwarza
przyłożone do ośrodka (półprzewodnika) napięcie.
Gęstość prądu unoszenia
elektronów:
J nu = qµ n nE
Gęstość prądu unoszenia dziur:
J pu = qµ p pE
gdzie ruchliwość ładunków dana jest równaniami (Einsteina):
q
q
µn =
Dn
µp =
Dp
kT
kT
kT
- potencjał termiczy złącza, w temp. pokojowej (300K) równy
ϕT =
q około 26mV
9
Półprzewodniki – transport nośników
nadmiarowych
Całkowita gęstość prądu elektronów:
J n = qµ n nE + qDn grad (n )
Całkowita gęstość prądu dziur:
J p = qµ p pE − qD p grad ( p )
Całkowity prąd w półprzewodniku:
J = Jn + J p
Złacze P-N - wprowadzenie
Złacze P-N niespolaryzowane
10
Złacze P-N niespolaryzowane
Stan równowagi złącza (brak zewnętrznej polaryzacji):
J pd − J pu = 0
J nd − J nu = 0
Prąd wypadkowy jest równy zeru, brak napięcia na
zaciskach złącza.
Złącze wykonuje się z jednorodnego półprzewodnika o
jednakowej koncenracji domieszek jednego typu, do którego
części wprowadzono domieszki typu drugiego.
Złacze P-N niespolaryzowane
Charakter zmian właściwości półprzewodnika (z n na p
lub z p na n) może występować skokowo lub w sposób
ciągły (aproksymacja liniowa)
Złacze P-N spolaryzowane
Uproszczony model elektryczny złącza PN
11
Złacze P-N spolaryzowane zaporowo
Przepływ
niewielkiego
prądu
nasycenia
Złacze P-N spolaryzowane w kierunku
przewodzenia
Przepływ
dużego prądu
dyfuzjii
Złacze P-N spolaryzowane w kierunku
przewodzenia
Prawdopodobieństwo przejścia cząstki przez barierę
energetyczną (warstwę zaporową) wynosi:
W
P = exp −
kT
Bariera energetyczna jest równa energii pola elektrycznego
w warstwie zaporowej:
W = q(U D − U )
Prąd dyfuzjii wynosi:
q(U D − U )
I d = a exp −
kT
12
Złacze P-N spolaryzowane w kierunku
przewodzenia
W stanie równowagi (bez polaryzacjii):
qU D
I d = I u = a exp −
kT
Stąd można zapisać:
qU
kT
Prąd całkowity (równanie Shockleya dla złącza idealnego):
I d = I u exp
U
I = I d − I u = I R exp − 1
ϕT
ϕT =
kT
- potencjał termiczny złącza, IR – efektywny prąd nasycenia
q
Złacze P-N spolaryzowane w kierunku
przewodzenia
Efektywny prąd nasycenia złącza (bez uwzględniania
generacji nośników w warstwie zaporowej):
D p pn Dn n p
I R = I S = q
+
L
Ln
p
gdzie:
Dp,n – współczynniki dyfuzji dziur i elektronów
Lp,n – drogi dyfuzji dziur i elektronów
pn,np – koncentracje nośników mniejszościowych
Złącze P-N – model pasmowy
13
Złącze P-N – model pasmowy
Złącze P-N – napięcie dyfuzyjne
Wyznacza się z zależności:
N N
U D = ϕT ln A 2 D
ni
Przykładowo, w temperaturze pokojowej, przy umiarkowanej
koncentracji domieszek NA=ND=1022 m-3:
- dla krzemu:
10 44
= 699mV
U D = 26mV ln
32
2.1025 ⋅10
- dla germanu:
10 44
= 313mV
U D = 26mV ln
38
5.76 ⋅10
Złącze P-N – charakterystyka prądowo –
napięciowa w kierunku przewodzenia
Wpływ rezystancji szeregowej – zastępczej liniowej
rezystancji będącej sumą rezystancji pasożytniczych:
U CC = IRS + U D
14
Złącze P-N – charakterystyka prądowo –
napięciowa w kierunku przewodzenia
Charakterystyka rzeczywista złącza PN:
U
U
I = I G exp D − 1 + I S exp D − 1
2
ϕ
T
mϕ T
gdzie:
IG – prąd generacji – rekombinacji nośników w warstwie zaporowej dla małych
wartości napięć polaryzujących
m – wspólczynnik niedoskonałości złącza równy 1...2:
- m = 2 – zakres małych prądów (generacji – rekombinacji) oraz dużych
prądów
- m = 1 – zakres średnich prądów (dyfuzji)
Złącze P-N – charakterystyka prądowo –
napięciowa w kierunku przewodzenia
Złącze P-N – charakterystyka prądowo –
napięciowa w kierunku zaporowym
Polaryzacja dużym napięciem wstecznym – wzrost pola
elektrycznego w półprzewodniku – nachylenie pasm w
modelu pasmowym:
Zrównanie poziomów
energetycznych znajdujących
się na brzegach pasm:
podstawowego i przewodzenia
Przebicie Zenera (jonizacja
elektrostatyczna) – tunelowe
przejście elektronów do pasma
przewodnictwa (półprz. silnie
domieszkowany) powodujące
wzrost koncentracji
swobodnych nośników ładunku
i przepływ prądu.
15
Złącze P-N – charakterystyka prądowo –
napięciowa w kierunku zaporowym
Dla silnych natężeń pola elektrycznego możliwa jest także jonizacja
atomów sieci półprzewodnika (półprzewodnik słabo
domieszkowany). Uderzenia elektronów, gdy są one w stanie
osiągnąć w ruchu energię o wartości większej niż szerokość pasma
zabronionego, wytrącają z atomów elektrony (tworzą się elektrony
swobodne) co powoduje powstawanie dziur. Zjawisko może nabrać
charakteru lawinowego (przebicie lawinowe) gdy odcinek
półprzewodnika z dużym natężeniem pola jest wystarczająco długi
(ma wiele dróg swobodnych dla nośników ładunku).
Złącze P-N – charakterystyka prądowo –
napięciowa w kierunku zaporowym
Złącza o napięciu przebicia poniżej 6V – przebicie Zenera
Złącza o napięciu przebicia powyżej 7V – przebicie lawinowe
Może także nastąpić
przebicie złącza które
bezpowrotnie niszczy
jego strukturę!!!!!!
Złącze P-N – pojemności złącza
Pojemność złączowa – występuje przy polaryzacji
wstecznej złącza PN
C j0
Cj =
m
U
1 − U
D
Dielektryk
UD + U
P
-
-
-
-
-
-
+
+
+
+
+
+
+
+
N
+
+
+
+
+
+
+
+
Warstwa
zaporowa
U
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Dla krzemu:
m = 1/2 - złacze skokowe
Ju
m = 1/3 – złącze liniowe
+
-
16
Złącze P-N – pojemności złącza
Pojemność:
S
C = ε 0ε r
d
ε 0 = 8.854 ⋅10 −12
F
m
Złącze P-N – pojemności złącza
Pojemność dyfuzyjna – powstaje przy polaryzacji złącza PN w
kierunku przewodzenia. Związana jest z występowaniem w bazie
złącza (obszarach P i N) nadmiarowych nośników mniejszościowych
związanych ze zmianami (szybkimi) napięcia polaryzującego oraz
skończonym czasem życia nośników. Zmiana napięcia powoduje
zmagazynowanie na czas związany z czasem życia nośników, pewnej
liczby nośników mniejszościowych, które po wspomnianym czasie
rekombinują.
Cd =
Iτ
2U D
τ – czas życia (przejścia) nośników
mniejszościowych w obszarze bazy złącza
Złącze P-N – wpływ temperatury złącza
spolaryzowanego w kierunku przewodzenia
Przy polaryzacji w kierunku przewodzenia:
U
q U
I = I R exp
− 1 = I R exp
kT m
mϕ T
− 1
Np.: dla I = 2mA, ze
wzrostem temperatury
napięcie na złączu
spada o około 2mV/0C
17
Złącze P-N – wpływ temperatury złącza
spolaryzowanego w kierunku przewodzenia
Złącze P-N silnie domieszkowane
Dla polaryzacji zaporowej istnieje możliwość przejścia
tunelowego elektronu z pasma podstawowego do pasma
przewodnictwa – prąd Zenera.
Dla polaryzacji w kierunku przewodzenia istnieje także
możliwość przejścia elektronu z pasma przewodzenia do
pasma podstawowego – prąd Esakiego (silnie
domieszkowane półprzewodniki i cienka warstwa
zaporowa)
W stanie równowagi:
IZ + IE = 0
Złącze metal - półprzewodnik
Praca wyjścia – bariera energetyczna jaka musi pokonać
elektron żeby wyjść z ciała stałego i oddalić się na
nieskończenie dużą odległość (gdy już nie ma
oddziaływania elektron-ciało stałe). Czasami jest ona
definiowana jako różnicą energi poziomu Fermiego i
energii elektronu w próżni. Am, Ap – praca wyjścia
elektronu z metalu i półprzewodnika.
Właściwości styku metal - półprzewodnik zależą od
wartości Am, Ap tych materiałów.
Rozpatrujemy dwa przypadki: Am>Ap i Am<Ap
18
Złącze metal - półprzewodnik
Dla Am>Ap, półprzewodnik typu ‘n’:
- po zetknięciu metalu i półprzewodnika elektrony przechodzą do metalu
ponieważ mają mniejszą pracę wyjścia,
- ruch w drugą stronę jest niemożliwy
- opuszczając półprzewodnik zostawiają w nim nieskompensowane jony
donorów (ładunek dodatni)
- na powierzchni metalu wytwarzają warstwę ładunku ujemnego
- czyli na powierzchni styku wytwarza się warstwa ładunku
przestrzennego i powstaje pole elektryczne
- cofa ono część elektronów do półprzewodnika
- proces odbywa się do momentu równowagi prądów elektronów
płynących do metalu i elektronów cofanych
Złącze metal - półprzewodnik
- większość obszaru warstwy ładunku przestrzennego znajduje się po
stronie półprzewodnika
- obszar ten ma zmniejszoną koncentrację elektronów więc ma
zwiększoną rezystancję – tworzy się warstwa zaporowa
- przykładając zewnętrzne napięcie do złącza można regulować
szerokość warstwy zaporowej jak w złączu PN
Polaryzacja:
- zaporowa: ‘+’ do półprzewodnika, ‘-’ do metalu
- przewodzenia: ‘-’ do półprzewodnika ‘+’ do metalu
Złącze metal - półprzewodnik
Równanie złącza:
U U
I = AT 2 exp − B exp
ϕT ϕT
− 1
gdzie: UB – wysokość powierzchniowej bariety potencjału na styku
A – stała Richardsona, współczynnik zależny od rodzaju
półprzewodnika; dla Si A=250 A⋅cm-2⋅K-2
19
Złącze metal - półprzewodnik
Właściwości złącza:
- mniejsze napięcie dyfuzyjne od złącza PN (około 0.3V)
- szybkie działanie ze względu na brak efektów bezwładnościowych
obserwowanych w złączu PN (szybkie oddawanie energii przez tzw.
elektrony gorące wpływające do metalu z półprzewodnika)
- duża stromość charakterystyki w zakresie przewodzenia
W przypadku półprzewodnika typu ‘p’ podobne właściwości
uzyskujemy dla warunku Am<Ap.
Złącze omowe
Złącze omowe musi spełniać dwa warunki:
- liniową zależność pomiedzy napięciem i prądem czyli nieskończona
szybkość rekombinacji nośników mniejszościowych (τ ≈ 0)
- małą rezystancję styku – brak bariery dla nośników większościowych
czyli metal musi być niewyczerpalnym źródłem i jednocześnie
nieskończonym odbiornikiem nośników większościowych
Spełniają te założenia złącza metali z pórzewodnikami:
typu ‘n’ dla Am<Ap oraz typu ‘p’ dla Am>Ap z pewnymi
modyfikacjami.
Złącze P-N – modelowanie złącza. Modele
nieliniowe
U
I = I G exp D
2ϕT
U
− 1 + I S exp D
m ϕT
− 1
U
I = I R exp
− 1
mϕT
I = I R = I S + IG
20
Złącze P-N – modelowanie złącza. Modele
nieliniowe
Złącze P-N – modelowanie złącza. Modele
liniowe
rd =
IQ
mϕ T
rd (ω ) =
rd (m.cz )
ωτ
Cd (ω ) = Cd (m.cz .)
2
ωτ
2
Podsumowanie
Model półprzewodnika
Złacze PN
Model diody półprzewodnikowej
21