Prawa Ohma i Kirchhoffa

Ćwiczenie nr 46
Prawa Ohma i Kirchhoffa
I Wstęp teoretyczny.
Do pomiaru prądu, napięcia, rezystancji i mocy służą odpowiednie mierniki, dzielące
się ze względu na przeznaczenie na: amperomierze, woltomierze, omomierze i watomierze.
W większości opierają się one na zjawisku elektromagnetyzmu. Główną część takiego
miernika stanowi jego ustrój pomiarowy, skłądający się z części nieruchomej i ruchomego
organu miernika. Organ ruchomy, połączony ze wskazówką, wykonuje z reguły ruch
obrotowy pod wpływem działających na niego sił, np. w wyniku oddziaływania pola
magnetycznego na prąd w cewce organu ruchomego. Do organu ruchomego przyczepiona jest
sprężyna, która przeciwdziała jego ruchowi. Wskazówka miernika ustawia się w położeniu, w
którym moment napędowy miernika równoważy się z momentem zwrotnym sprężyny, a
ponieważ jej moment zwrotny jest proporcjonalny do kąta jej skręcenia, kąt odchylenia
organu ruchomego jest proporcjonalny do momentu napędowego. Aby wytłumić niepożądane
wielokrotne wahnięcia wskazówki, stosuje się tłumiki, magnetyczne i powietrzne.
Pod względem budowy, mierniki korzystające z sił magnetycznych dzielą się na
magnetoelektryczne, elektromagnetyczne, elektrodynamiczne, i ferrodynamiczne. Zasada
działania miernika magnetoelektrycznego polega na oddziaływaniu pola magnesu trwałego na
umieszczoną w tym polu cewkę, przez którą płynie prąd. Miernik elektromagnetyczny składa
się z cewki, przez którą płynie prąd, i jednego lub kilku rdzeni ze stali magnetycznie miękkiej.
Mierniki elektrodynamiczne działają dzięki oddziaływaniu elektrodynamicznemu dwóch
cewek, przez które płyną prądy. Ze względu na wysoką cenę, są używane wyłącznie jako
mierniki laboratoryjne do dokładnych pomiarów. Podobnym miernikiem jest miernik
ferrodynamiczny. Istnieją także inne mierniki, np. cieplne i termoelektryczne, jak i
elektrostatyczne. Najnowsze mierniki cyfrowe, oparte na tranzystorach, są jednak
dokładniejsze niż wszelkie pozostałe mierniki, ze względu na brak części ruchomych i
precyzyjność układów scalonych.
Wartość wskazana przez dowolny miernik może się różnić od wartości rzeczywistej
mierzonej wartości. Różnica ta nazywa się błędem bezwzględnym miernika; zaś jej stosunek
do maksymalnej wartości zakresu pomiarowego nazywa się błędem względnym, podawanym
zwykle w procentach. Dokładność (błąd względny) wszystkich mierników pozwala na
zaliczenie ich do odpowiedniej klasy dokładności. W Polsce stosuje się następujące klasy
dokładności: 0.1, 0.2, 0.5, 1, 1.5, 2.5. Liczba oznaczająca klasę dokładności miernika określa
największy dopuszczalny błąd względny miernika. Stąd widać, że im mniejsze odchylenie
wskazówki, tym większy może być błąd procentowy pomiaru. Mierniki laboratoryjne zwykle
są klasy 0.1, 0.2 i 0.5 i służą do dokładnych pomiarów w laboratoriach, jak i sprawdzania
mierników technicznych, o pozostałych klasach dokładności.
Przy pomiarach obwodów elektrycznych rozgałęzionych poza miernikami przydaje się
m.in. znajomość prawa Kirchhoffa. Pierwsze prawo Kirchhoffa mówi że suma agebraiczna
prądów schodzących się w dowolnym węźle obwodu elektrycznego (jeżeli prądom
dopływającym do węzła przypisze się znak “+”, a prądom odpływającym znak “-“) jest równa
zeru. Jest to tzw. bilans prądów w węźle obwodu elektrycznego. Wg. drugiego prawa
Kirchoffa, w dowolnym oczku obwodu elektrycznego prądu stałego suma spadków napięć na
elementach rezystancyjnych oczka jest równa sumie działających w tym oczku sił
elektromotorycznych, gdzie oczkiem nazywamy zbiór gałęzi tworzących jedną zamkniętą
drogę dla przepływu prądu:
E  RI
Przyjąwszy dowolny obieg oczka, np. zgodny z obiegiem wskazówek zegara, to suma
napięć źródłowych i odbiorczych w oczku jest równa zeru.
Korzystając bezpośrednio z prawa Kirchhoffa można także udowodnić zasadę, że
natężenia prądu w gałęziach oporowych połączonych równolegle są proporcjonalne do ich
przewodności albo odwrotnie proporcjonalne do ich oporów.
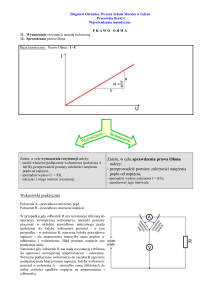
Drugim użytecznym prawem przy badaniu obwodów elektrycznych jest Prawo Ohma.
Wg. Ohma, wartość prądu w przewodniku jest wprost proporcjonalna do przyłożonego do
jego końców napięcia, a odwrotnie proporcjonalna do rezystancji przewodnika: I=U/R
Dalsze badania Ohma wykazały, że opór elektryczny jest proporcjonalny do długości l
przewodu, odwrotnie proporcjonalny do przekroju S przewodu, a ponadto zależy od rodzaju
materiału z jakiego przewód został wykonany:
l
R
S
Jeden om jest rezystancją gdy róznica napięć jednego wolta wywołuje w przewodzie prąd o
wartości jednego ampera.
II. Opis doświadczenia
Celem doświadczenia było zastosowanie praw Ohma i Kirchhoffa, w celu porównania
wyników zmierzonych bezpośrednio wartości prądów z wartościami obliczonymi korzystając
z ww. praw, dla dwóch układów, zbudowanych wg. schematu (bez i z opornikiem R5).
Po złożeniu układów wg. odpowiednich schematów, zmierzono opór każdego opornika.
Następnie starano się utrzymać stałe napięcie zasilające wynoszące 10 V, podczas gdy
mierzono różnice napięć na opornikach, jak i natężenie prądu w gałęziach I1 do I5.
III. Opracowanie wyników pomiarów:
Opierając się na zmierzonych wartościach oporu oporników i wartości napięcia
wejściowego, można łatwo obliczyć także wartości napięć i natężeń prądów przepływających
przez poszczególne oporniki. Schemat pierwszy można rozbić na dwie części, tą z
opornikiem R1, i tą z pozostałymi trzema, z których dwa są połączone szeregowo, a
równolegle z trzecim. Wiemy, że opór gałęzi przez którą płynie prąd I3 wynosi R3 + R4, czyli
w naszym przypadku 2.94 k. Ponieważ opór opornika R2 wynosi 0.192 k, ze wzoru
1/R=1/R1+1/R2 otrzymujemy opór całego oczka jako 0.180 k. Stąd opór całego obwodu
wynosi 0.180+0.868=1.048 k. Korzystając z prawa Ohma, I=U/R, możemy łatwo znaleźć
natężenie przepływu prądu przez cały układ: I=10V/1.048k = 9.54 mA. Jest to natężenie
prądu w punkcie I1. Z tego samego wzoru możemy wyliczyć napięcie na oporniku R1: U = RI
= 0.868 k * 9.54 mA = 8.28 V. Stąd też wiemy, jakie napięcie powstaje na dużym oczku:
10V-8.28V=1.72V.
Obliczamy wartość prądu płynącego przez opornik R2:
I2=1.72/0.192=8.96mA, jak i przez oporniki R3 i R4: I3=I4=1.72/(0.550+2.390)=0.585mA. Z
tego samego wzoru też już wiemy jakie napięcia na nich występują:
U3=RI=0.550*0.585=0.322 V, U4=2.390*0.585=1.40 V
Wstawiamy powyższe wyniki w tabelkę i porównujemy z wynikami otrzymanymi z
bezpośrednich pomiarów:
Prąd
I1
I2
I3
Natężenie zmierzone [mA]
9.58
8.86
0.564
Natężenie wyliczone [mA]
9.54
8.96
0.585
Dla drugiego schematu wyliczymy prądy podstawiając zmierzone opory i napięcia do
wzoru I=U/R , gdzie otrzymujemy:
Prąd
I1
I2
I3
I4
Natężenie zmierzone [mA]
16.57
13.88
5.63
2.42
Natężenie wyliczone [mA]
8.41
14.06
5.69
2.44
IV. Ocena błędu
Dla ostatniego przykładu (gdzie korzystaliśmy ze wzoru I=U/R), policzymy błąd
metodą różniczki zupełnej:
I
I
1
U
I 
U 
R  U  2 R 
U
R
R
R
1
584
.
 0.01 
 1  0.0052mA
2390
2390 2
co dając błąd względny rzędu 0.2% jest bardzo niską wartością.
V. Wnioski
Porównując wartości prądu zmierzone bezpośrednio z wyliczonymi, okazuje
się, że wyniki są zbieżne, pomijając drobne różnice rzędu 1-2%, które prawdopodobnie
wynikały z nieprecyzyjności elementów obwodu i ich połączeń. Poza tym trzeba wziąć pod
uwagę możliwość nagrzewania się oporników i co za tym idzie zmiany w ich przewodności.
Dodatkowo błędnie zmierzono jedną z wartości natężenia prądu (dla I1, schemat 2); być może
z powodu obluzowania się jednego z połączeń w obwodzie lub źle ustawionego trybu pracy
miernika. Niemniej, widać, że prawa Ohma i Kirchhoffa sprawdzają się także w przypadku
bardziej skomplikowanych obwodów, a dodanie dodatkowego opornika jedynie zwiększa
liczbę wymaganych pomiarów.