Komórka nerwowa - neuron
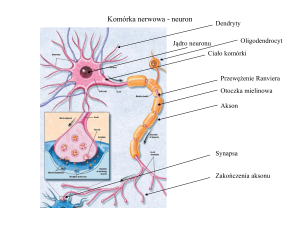
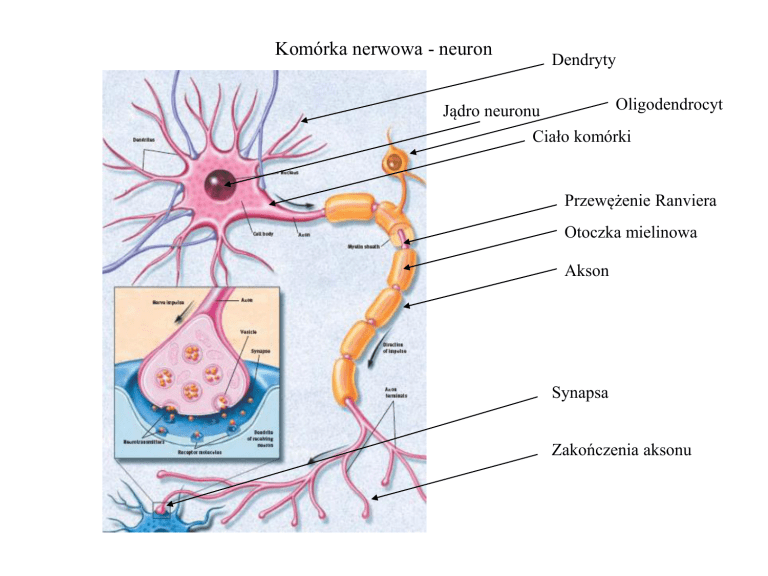
Dendryty
Oligodendrocyt
Jądro neuronu
Ciało komórki
Przewężenie Ranviera
Otoczka mielinowa
Akson
Synapsa
Zakończenia aksonu
Komórka nerwowa - neuron
Neurony
jednobiegunowe
Neuron dwubiegunowy
Średnica aksonu
od 4 (0,004 mm) do 100 mikronów (.1 mm)
Średnica włosa
0,02 mm do 0,08 mm.
Neurony wielobiegunowe
Długość aksonu od 1 mm do ponad 1m
U ludzi:
Ok. 1011 neuronów w mózgu
Każdy neuron ok. 104 połączeń
Średnia długość aksonu w korze ok. 0.06 m.
Całkowita długość aksonów A = 6*109m
Odległość Ziemia – Księżyc L = 4* 108m
A/L = 15
Komórka nerwowa - terminologia
Neurony posiadające
długi akson, który tworzy
połączenie z innym
rejonem układu
nerwowego nazywają się
neuronami projekcyjnymi,
neuronami głównymi i
komórkami
przekaźnikowymi.
Neurony wewnętrzne lub
interneurony znajdują się
w całości wewnątrz
jednego obszaru układu
nerwowego. Neurony
wewnętrzne mogą nie
posiadać aksonu.
Dendryty - terminologia
Neurony posiadają
zazwyczaj jeden akson
oraz wiele dendrytów.
Wyróżniamy dendryty
wierzchołkowe (apical) i
podstawne (basal).
Druga składowa układu nerwowego komórki gleju
Komórki glejowe
Komórki glejowe są drugim
głównym składnikiem układu
nerwowego. W niektórych
obszarach są 10 razy liczniejsze niż
neurony.
Najważniejszą rolą komórek
glejowych jest kontrolowanie
otoczenia neuronów. Są one
zaangażowane w wiele różnych
funkcji
Rodzaje i funkcje gleju
•Astrocyty: największe i najliczniejsze. Ich funkcja to
podtrzymywanie fizyczne i odżywianie neuronów,
regulacja zawartości przestrzeni zewnątrzkomórkowej
- buforowanie jonów, regulacja neuroprzekaźnictwa
(pochłanianie neurotransmitera i zapobieganie dyfuzji
poza szczelinę synaptyczną), bariera krew – mózg (?).
•Microglia: składniki układu odpornościowego,
aktywne podczas stanów zapalnych, usuwają ‘zmarłe’
neurony.
•Oligodendrocyty: wytwarzają mielinę w neuronach
centralnego układu nerwowego.
•Komórki satelitarne (Satellite Cells):
podtrzymywanie fizyczne neuronów w obwodowym
układzie nerwowym
•Komórki Schwanna: wytwarzają mielinę w
neuronach obwodowego układu nerwowego.
Stwardnienie rozsiane (łac. sclerosis multiplex, SM) - demielinizacja włókien
nerwowych w obrębie mózgu i rdzenia kręgowego
Potencjał błonowy
Potencjał błonowy – różnica potencjałów
w poprzek błony komórkowej
Potencjał błonowy bierze się z
rozdzielenia dodatnich i ujemnych
ładunków przez błonę komórkową. W
neuronach na zewnątrz występuje
przewaga jonów dodatnich, a wewnątrz
– ujemnych.
Potencjał błonowy jest podstawową własnością wszystkich żywych komórek
Techniki pomiarowe mikropiptety
Mikropipety służą do pomiarów
potencjału zewnątrzkomórkowego,
wewnątrzkomórkowego, patch,
stymulacji elektrycznej,
dostarczania substancji do
przestrzeni zewnątrz/
wewnątrzkomórkowej
Pomiary wewnątrzkomórkowe in vivo. Grupa prof. Amzici, Universite Laval, Quebec, Kanada
Techniki pomiarowe – patch clamp
(E. Neher, B. Sakmann, Nobel 1991)
Pipeta do patch calmp. Zakończenie pipety
może być większe (średnica~3mm) niż
mikropipety do pomiarów
wewnątrzkomórkowych (średnica ~1 mm)
Mikropipety do patch clamp są przygotowywane jak
zwykłe mikropipety lecz ich zakończenia są gładkie i
przyklejają się do błony zamiast ją przekłuwać. Patch
clamp umożliwia pomiar z pojedynczych kanałów
jonowych (indside-out) oraz potencjału błonowego
Układ pomiarowy patch clamp
Techniki pomiarowe – patch clamp
(E. Neher, B. Sakmann, Nobel 1991)
Pomiar potencjału błonowego (whole cell recording) komórki hipokampa metodą patch calmp. Pipeta jest
zaznaczona kolorem niebieskim.
Siły chemiczne i elektryczne
C1
WC 2.3RT log
C2
R – stała gazowa
T - temperatura
WE qV zFV
F – stała Faradaya
V – różnica potencjałów
z - walencyjność
Potencjał Nernsta
Stan równowagi:
WE WC
C1
zFV 2.3RT log
C2
RT
C1
V 2. 3
log
zF
C2
Równanie Nernsta
Walter Hermann Nernst (ur. 25 czerwca 1864 w
Wąbrzeźnie, zm. 18 listopada 1941w Zibelle), laureat
Nagrody Nobla z chemii w 1920r.
V - Potencjał Nernsta, potencjał równowagi,
potencjał dyfuzji
Potencjał Nernsta
RT
[ K ]out
VK 2.3
log
F
[ K ]in
[ K ]out
VK 58 log
mV
[ K ]in
58 log
VNa
5
mV 81mV
125
[ Na ]out
58 log
mV
[ Na ]in
58 log
120
mV 58mV
12
[Cl ]in
VCl 58 log
mV
[Cl ]out
58 log
5
mV 81mV
125
Potencjał błonowy - równanie Goldmana
P K [ K ]out P Na [ Na ]out PCl [Cl ]in
Vm 58 log
mV
P K [ K ]in P Na [ Na ]in PCl [Cl ]out
P – przepuszczalność (permeability) [m/s]
Równanie Goldmana
Równanie Goldmana-Hodgkina-Katza (GHK)
Uwagi:
- Cl- ma ładunek ujemny i dlatego stosunek stężeń jest odwrócony.
- Ponieważ [K+]out = [Cl-]in oraz [K+]in = [Cl-]out i PCl << PK, to
pominięcie Cl- znacząco nie zmieni wyniku.
Dla PNa = 0.04*PK, zaniedbując Cl-:
Vm = -60 mV
Obwód zastępczy
Obwód zastępczy błony komórkowej neuronu. Potencjał równowagowy jest
reprezentowany przez baterię o odpowiedniej polaryzacji i napięciu odpowiednim dla
danego jonu. Bateria jest połączona szeregowo z opornością (R) odpowiadającą
przepuszczalności błony. Zazwyczaj, zamiast oporności podaje się przewodnictwo G =
1/R, związane z przepuszczalnością (P) i stężeniami jonów ([K]) następująco:
[ K ]out
GK PK
[ K ]in
Dodatkowo, podwójna warstwa lipidowa tworząca błonę może gromadzić ładunki i
zachowuje się jak kondensator o pojemności Cm.
Potencjał czynnościowy
Potencjał czynnościowy polega na krótkotrwałej depolaryzacji
błony komórkowej. Wczesne doświadczenia (K.C. Cole i H. J.
Curtis, 1939) pokazały, że błona komórkowa staje się
spolaryzowana dodatnio (ok. +50 mV) podczas maksimum
potencjału czynnościowego.Gdyby powodował go jedynie
chwilowy wzrost przepuszczalności dla wszystkich jonów,
błona osiągnęła by 0 mV, lecz nie więcej. Obiektem do badań
potencjału czynnościowego był akson Kalmara Atlantyckiego
Kalmar Atlantycki Loligo pealei
Potencjał czynnościowy – impuls sodowy
Zależność potencjału
czynnościowego od stężenia sodu. A
i B: Maksimum potencjału
czynnościowego maleje wraz
maleniem stężenia Na w płynie
zewnątrzkomórkowym. Silna
zależność wartości maksimum od
stężenia Na wskazuje na duża
przepuszczalność błony dla tych
jonów w trakcie impulsu.
Alan Hodgkin i Bernard Katz odkryli, że amplituda potencjału czynnościowego
zależy od koncentracji Na na zewnątrz komórki. Postawili hipotezę, że chwilowa
zmiana przepuszczalności i wpływ jonów Na do wnętrza komórki powoduje
potencjał czynnościowy. Potwierdzeniem tej hipotezy była obserwacja, że
maksimum potencjału czynnościowego wynosi +55mV, co jest bliskie wartości
potencjału równowagi dla sodu. Ich eksperymenty wskazały również, że zanik
potencjału czynnościowego może być związany ze wzrostem przepuszczalności dla
jonów K i ich wypływem z komórki.
Potencjał czynnościowy – wszystko albo nic!
wzrost gNa
depolaryza
-cja błony
napływ
Na+
‘Wybuchowa’ natura impulsu jest związana z kanałami sodowymi o przepuszczalności zależnej od
napięcia i sprzężeniem zwrotnym dodatnim z depolaryzacją błony.
Skąd się bierze próg?
Depolaryzacja podprogowa jest kompensowana pasywnym wypływem jonów potasu i nie
wywołuje potencjału czynnościowego. Jeśli wypływ jonów potasu nie może zrównoważyć
wpływu jonów sodu, błona osiąga próg na generację impulsu i generowany jest potencjał
czynnościowy.
Okresy refrakcji
Po wystąpieniu potencjału czynnościowego występuje okres refrakcji. W fazie refrakcji
absolutnej komórka nie może wygenerować kolejnego impulsu bez względu na pobudzenie. W
fazie refrakcji względnej, komórka może wygenerować impuls ale wymaga to silniejszego
pobudzenia niż w stanie spoczynku.
Voltage clamp
Technika voltage clamp była opracowana przez Kenneth’a Cole’a w 1949 r. Alan Hodgkin i
Andrew Huxley wykorzystał ją w serii eksperymentów (1952) nad mechanizmem generacji
potencjału czynnościowego. Voltage clamp pozwala mierzyć wpływ zmian potencjału
błonowego na przewodnictwa jonowe.
Voltage clamp działa na zasadzie ujemnego sprzężenia zwrotnego. Potencjał błonowy jest mierzony przez
wzmacniacz podłączony do elektrod zewnątrz i wewnątrzkomórkowej. Jest on przekazywany do wzmacniacza
(feedback amplifier). Drugie wejście do wzmacniacza stanowi potencjał z generatora ustalany przez
eksperymentatora (command potential). Wzmacniacz oblicza różnicę napięć i przekazuje sygnał na elektrodę
biegnącą wewnątrz komórki. Prąd potrzebny do utrzymania napięcia na zadanym poziomie jest miarą prądu
błonowego płynącego przez kanały jonowe.
Eksperyment Hodgkina i Huxleya - video
Eksperyment Hodgkina i Huxleya - wyniki
Mała depolaryzacja wywołuje prąd
kondensatora Ic = C dV/dt oraz leak Il.
Większa depolaryzacja wywołuje większy
prąd kondensatora Ic oraz Il oraz
dodatkowo prąd dokomórkowy a następnie
odkomórkowy.
Depolaryzacja w obecności tetrodoxyny
(TTX) blokującej kanały Na a następnie w
obecności tetraethyloammonium (TEA)
blokującej kanał K pozwala zobaczyć
‘czysty’ prąd IK i INa, po odjęciu Ic oraz Il.
•Fugu (puffer fish) specjał sushi zawierający TTX
•Szkolenie na mistrza fugu trwa 3 lata, test zdaje ok. 30%.
•Mimo wszystko, w Japonii, 5-10 osób rocznie umiera w wyniku spożycia fugu
Eksperyment Hodgkina i Huxleya - wyniki
Prawo Ohma
g K (V , t )
I K (V , t )
(V VK )
g Na (V , t )
I Na (V , t )
(V VNa )
Znając IK, INa, VK, VNa, oraz V można obliczyć gK i gNa. IK, INa można wyliczyć z pomiarów voltage clamp, VK,
VNa- stałe, V – ustala eksperymentator.
Andrew Huxley, Alan Hodgkin (Nobel 1963)
dV
I m Cm
I K I Na I L
dt
dV
I m Cm
g K (V , t )(V VK ) g Na (V , t )(V VNa ) g L (V VL )
dt
HH model - bramki
Pomiary voltage clamp dla różnych wartości V pozwoliły HH postawić hipotezę, że kanał Na posiada
bramkę aktywacyjną i bramkę inaktywacyjną. Obie muszą być otwarte by kanał mógł przewodzić jony.
Bramka aktywacyjna jest zamknięta gdy błona znajduje się poniżej potencjału spoczynkowego i otwiera
się szybko przy depolaryzacji. Bramka inaktywacyjna jest otwarta przy potencjale spoczynkowym i
wolno zamyka się w wyniku depolaryzacji. Kanał K posiada tylko bramkę aktywacyjną otwierającą się
wolno w wyniku depolaryzacji.
Zachowanie
pojedynczych
kanałów może być
rejestrowane za
pomocą patch clamp.
W zapisach widać
szybkie otwieranie i
zamykanie
pojedynczych
kanałów. Ich suma
daje gładki przebieg
wartości prądu
Model bramki (gate model – Hodgkin i Huxley (1952))
Zamknięty
a
Otwarty
1-y
y
b
y - prawdopodobieństwo, że bramka jest
w stanie otwartym, 1-y – że w stanie
zamkniętym, a, b – stałe szybkości.
Zakładamy kinetykę reakcji pierwszego rzędu:
dy
a (1 y ) by
dt
W stanie ustalonym:
dy
0 a (1 y ) by
dt
Stąd:
y
a
a b
Podstawiając do równania:
dy
a (1 y) by a (a b ) y y (a b ) (a b ) y
dt
(a b )( y y)
Model bramki (gate model – Hodgkin i Huxley (1952))
Całkując dostajemy:
dy(1)
(1) (a b)dt
(y y)
ln( y y) (a b)t
y y Ae (a b )t
y (V )
stan ustalony
1
(V )
a (V ) b (V )
stała czasowa
Zależność stałych czasowych i prawdopodobieństwa w stanie ustalonym od napięcia dla kanałów napięciowozależnych
aktywowanych depolaryzacja (lub inaktywowanych hiperpolaryzacją).
HH model
HH zauważyli, że gK i gNa nie są funkcjami exp(-t/) lecz raczej potęgami funkcji ekspotencjalnych.
Zaproponowali:
gK (V , t ) YK (V , t ) g K n4 g K
g Na (V , t ) YNa (V , t ) g Na m3h g Na
Korzystając z modelu bramki:
dn
an
1
a n (1 n) b n n, n
, n
dt
a n bn
a n bn
dm
am
1
a m (1 m) b m m, m
, m
dt
a m bm
a m bm
dh
ah
1
a h (1 h) b h h, h
, h
dt
a h bh
a h bh
HH model
Rozwiązując równania na n, m i h dostajemy:
n(t ) n0 [( n0 n )(1 et / n )]
m(t ) m0 [( m0 m )(1 et / m )]
h(t ) h0 [( h0 h )(1 et / h )]
Wstawiając rozwiązania do gNa i gK dostajemy:
gK (t ) gK n4 gK [n0 (n0 n )(1 et / n )]4
g Na (t ) g Na m3h
g Na [m0 (m0 m )(1 et / m )]3[h (h0 h )(1 et / h )]
g Na m h0 (1 et / m )3 et / h
Gdyż m0 i hinf są zaniedbywalnie małe.
HH model
Z przebiegów gK i gNa HH wyznaczyli:
a n , bn , a m , bm ,a h , bh
A następnie obliczyli:
1 n
n
, bn
am
m
, bm
ah
nh
, bh
an
n
m
h
n , m , h , n , m , h
n
1 m
m
1 nh
h
HH model
Po dopasowaniu am an ah bm bn bh oraz numerycznym rozwiązaniu równań HH, otrzymano
doskonalą zgodność z doświadczeniem. Model HH jest wciąż uznawany za największy sukces
w ilościowym modelowaniu mózgu a nawet i w całych naukach biologicznych. Teoria HH
opisuje nie tylko generację potencjałów czynnościowych ale również ich propagacje.
Model HH ma tez pewne ograniczenia. Dobrze opisuje makroskopowe prądy Na lecz jego
przewidywania na poziomie pojedynczych kanałów nie zgadzają się z doświadczeniem (np.
bramki m nie są od siebie niezależne i nie koniecznie są takie same).
W równaniach HH można zaobserwować
zachowania chaotyczne
Generacja potencjału czynnościowego - podsumowanie
Charakterystyka typowego kanału
activation gate
inactivation gate
1
1
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0
-100
-80
-60 -40
mV
tau activation
0
-20
-100
-80
-60 -40 -20
mV
tau recovery and inactivation
-100
-80
15
300
ms
ms
10
5
0
200
100
-100
-80
-60
mV
-40
-20
0
-60
mV
-40
-20
Prądy w komórkach nerwowych
Kanały Ca+
Dwa rodzaje kanałów wapniowych rejestrowanych metodą patch clamp. A. T-type (transient lub LVA – low
voltage activation channel). B. L-Type (long lasting lub HVA – high voltage activated channel).
Kanały K+
IK(DR)+ IK(A)
Istnieje wielka różnorodność kanałów K+. W aktywnej
komórce, kanały K+ zapewniają powrót do stanu
równowagi. Potencjał równowagowy dla K+ (-81 mV)
jest bliski potencjałowi spoczynkowemu komórki (-70
mV). Po otwarciu kanałów Na+ lub Ca+, następuje
aktywacja kanałów K+ mająca na celu przywrócenie
potencjału spoczynkowego
IK(Ca)
Delayed rectifier IK(DR)
Transient IK(A)
Delay current IK(D)
Calcium-Dependent IK(Ca); IC
IK(DR)+IK(A)+IK(D)+IK(Ca) + IAHP+IM
Afterhyperpolarization IAHP
Anomalous rectifier IAR; IQ; Ih
M current IM
Leak IK, leak
Kanały jonowe - podsumowanie
Rozszerzony model błony neuronalnej
Cztery rodzaje neuronów kory?
W tradycyjnym ujęciu istniały cztery rodzaje zachowania neuronów kory
mózgowej i przypisywano im różne rodzaje komórek: RS – regular spiking,
FRB – fast rhythmic bursting, FS – fast spiking, IB – intrinsically bursting.
Zapisy wewnątrzkomórkowe in vivo pokazały, że komórki mogą zmieniać
wzorce odpalania w zależności od wartości potencjału błonowego.
a) zapisy wewnątrzkomórkowe u czuwających i śpiących kotów b) zapis wewnątrzkomórkowy z neuronu
korowego u kota w stanie anestezji. Podawanie prądu dokomórkowego (b1 - ramka) wywołuje zmianę wzorca
odpalania. Mircea Steriade, Neocortical Cell Classes Are Flexible Entities. NATURE REVIEWS |
NEUROSCIENCE, VOL. 5, pp. 121-134, 2004.