ZADANIA DODATKOWE Z FIZYKI – KLASA I
1. Wioślarz może nadać łódce prędkość 2,5 m/s. Prędkość nurtu rzeki wynosi 7,2 km/h. W jakim czasie
wioślarz wraz z łódką pokona odległość 500 m, poruszając się ruchem jednostajnym pod prąd rzeki?
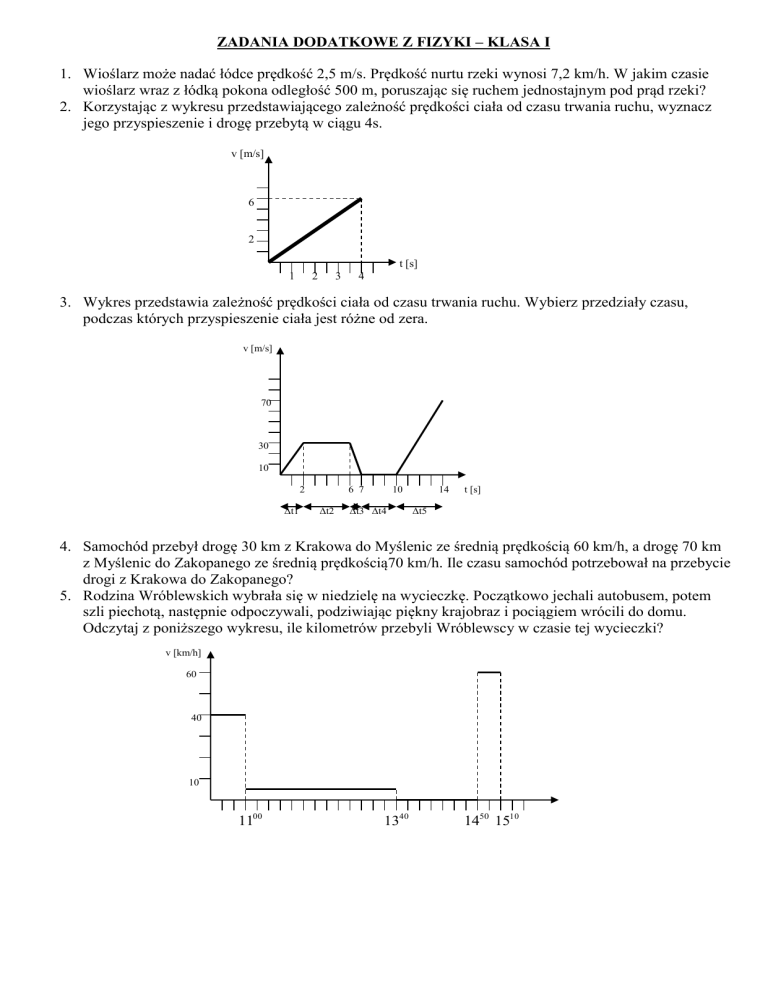
2. Korzystając z wykresu przedstawiającego zależność prędkości ciała od czasu trwania ruchu, wyznacz
jego przyspieszenie i drogę przebytą w ciągu 4s.
v [m/s]
6
2
t [s]
1
2
3
4
3. Wykres przedstawia zależność prędkości ciała od czasu trwania ruchu. Wybierz przedziały czasu,
podczas których przyspieszenie ciała jest różne od zera.
v [m/s]
70
30
10
2
Δt1
6 7
Δt2
10
Δt3 Δt4
14
t [s]
Δt5
4. Samochód przebył drogę 30 km z Krakowa do Myślenic ze średnią prędkością 60 km/h, a drogę 70 km
z Myślenic do Zakopanego ze średnią prędkością70 km/h. Ile czasu samochód potrzebował na przebycie
drogi z Krakowa do Zakopanego?
5. Rodzina Wróblewskich wybrała się w niedzielę na wycieczkę. Początkowo jechali autobusem, potem
szli piechotą, następnie odpoczywali, podziwiając piękny krajobraz i pociągiem wrócili do domu.
Odczytaj z poniższego wykresu, ile kilometrów przebyli Wróblewscy w czasie tej wycieczki?
v [km/h]
60
40
10
1100
1340
1450 1510
6. W chwili, gdy zapaliły się zielone światła, samochód A ruszyła ze skrzyżowania i został w tym
momencie wyprzedzony przez jadący samochód B. Na wykresie przedstawiono zależności szybkości
tych samochodów od czasu, jaki upłynął od zapalenia się zielonych świateł. Określa wartości
przyspieszeń samochodów A i B.
v [m/s]
35
25
15
5
2
4
6
8
10
12
t [s]
7. Prędkość światła w próżni w przybliżeniu jest równa 300000000 m/s. Ile to km/h?
8. Ciało o zerowej prędkości początkowej porusza się ruchem jednostajnie przyspieszonym. W czasie
pierwszych 4 sekund przebyło 24 metry. Jaką drogę przebędzie to ciało w pierwszych 8 sekundach
ruchu?
9. Tramwaj poruszał się z prędkością początkową 36 km/h i wyhamował w czasie 5 sekund, poruszając się
ruchem jednostajnie opóźnionym. Wyznacz opóźnienie i drogę hamowania tramwaju.
10. Wykres przedstawia zależność prędkości od czasu w pewnym ruchu. Określ drogę przebytą w
pierwszych 10 sekundach ruchu oraz przyspieszenie.
v [m/s]
5
10
t [s]
11. Oblicz, czy większy pęd ma mrówka o masie 0,5 g biegnąca z prędkością 18 km/h, czy żółw o masie
1kg „pędzący” z prędkością 1m/min.
12. Oblicz masę ciała poruszającego się z prędkością 72 km/h, jeżeli jego pęd wynosi 8000 kg m/s.
13. Jaką prędkość odrzutu uzyska działo o masie 10 ton po wystrzeleniu pocisku o masie 30 kg z prędkością
3000 km/h?
14. Wagon o masie 25 ton poruszający się z prędkością 2 m/s uderza w nieruchomy wagon o masie 15 ton i
następnie pcha go przed sobą. Oblicz prędkość wagonów po zderzeniu. (Wskazówka: skorzystaj z
zasady zachowania pędu i określ całkowity pęd przed zderzeniem i całkowity pęd po zderzeniu).
15. Na sanki o masie 2 kg poruszające się po lodowisku z prędkością 6 m/s położono paczkę o masie 10
kg. Z jaką prędkością będą poruszały się sanki z paczką? Tarcie między płozami sanek i lodem
pomijamy. (Wskazówka: zastosuj zasadę zachowania pędu).
16. Na nitkach wiszą jedna pod drugą trzy kulki (jak na rysunku) o ciężarach równych 30 N, 50 N, 20 N.
Jaką siłą naciągnięte są nitki I, II, III?
III
20N
II
50N
I
30N
17. Pierwszy wagon tramwaju ciągnie drugi wagon siłą 15000 N, a siła oporu ruchu wynosi 10000 N. Jaką
siła działa drugi wagon na pierwszy?
18. Stała, niezrównoważona siła o wartości 9 N przesuwa bez tarcia po poziomej płaszczyźnie dwa
połączone ze sobą klocki (rys.). Jaką siłą poruszany jest klocek drugi?
F2
m2 2kg
F1 9N
m1 1kg
19. Stosując odpowiednie prawa fizyczne uzasadnij słuszność następujących powiedzeń:
a) „Baba z wozu, koniom lżej”,
b) „Niedaleko pada jabłko od jabłoni”.
20. Wózek porusza się ruchem opisanym wykresem. Pęd tego wózka w miarę upływu czasu
a) rośnie;
b) maleje
droga
c) nie zmienia się;
d) nie można tego jednoznacznie określić.
Wyjaśnij dlaczego.
czas
ZADANIA DODATKOWE Z FIZYKI – KLASA II
1. Na podstawie poniższego rysunku wyznacz objętość kamienia wrzuconego do wody:
6 cm
4 cm
8 cm
8 cm
8 cm
8 cm
2. Wyjaśnij, w jaki sposób wyznaczysz gęstość mleka mając do dyspozycji wagę laboratoryjną z
odważnikami oraz menzurkę z podziałką.
3. Prostopadłościan o wymiarach: 3 cm, 25 cm i 1,2 m ma masę 5 kg. Jaka jest gęstość substancji, z której
wykonano prostopadłościan?
4. Z jakiej substancji wykonana jest kula o masie 226,72 kg i objętości 20 dm³?
5. Oblicz krawędź sześciennej kostki wykonanej z drewna, jeśli jej masa wynosi 0,55 kg.
6. Jakie jest pole podstawy prostopadłościanu o wysokości 1 m, wykonanego ze stali o gęstości 7500
kg/m³, jeśli jego masa wynosi 22,5 k? Wynik podaj w centymetrach kwadratowych.
7. Oblicz gęstość drewnianej bryły o ciężarze 1 kN i objętości 200 dm³.
8. Jaka jest masa aluminiowej kulki, jeżeli jej ciężar wynosi 6,4 kN?
9. W pierścionku znajduje się diamentowe oczko o ciężarze 0,005 N. Jaka jest objętość tego oczka? Wynik
podaj w centymetrach sześciennych.
10. Z jakiego metalu wykonano wisiorek, którego ciężar wynosi 0,2098 N, a objętość 2 cm³?
11. Klocek o masie 0,2 kg zostaje pchnięty po podłodze z prędkością początkową 2 m/s. Po przebyciu
pewnej drogi klocek zatrzymuje się. Jaka praca została wykonana podczas hamowania klocka? Czy
energia mechaniczna klocka zostaje zachowana w tym doświadczeniu?
12. W szklance znajduje się woda o temperaturze pokojowej. Wrzucono do niej kawałki topniejącego lodu.
Od tej chwili, co dwie minuty mieszano zawartość szklanki i mierzono temperaturę wody aż do jej
ustalenia się. Wyjaśnij, który szkic wykresu może ilustrować zmiany temperatury wody w szklance?
temperatura
IV
I
II
III
czas
13. Równanie t F 1,8t C 32 opisuje zależność, jaka istnieje między tą samą temperaturą wyrażoną w
stopniach Celsjusz i w stopniach Fahrenheita. Oblicz t C jaka odpowiada t F 50F .
14. Jaką ilość energii cieplnej trzeba dostarczyć wodzie o masie 0,5 kg i temperaturze 20ºC, aby ją ogrzać
do temperatury 100ºC?
15. Jaka była masa gliceryny, jeżeli po dostarczeniu jej energii cieplnej równej 200 kJ jej temperatura
podniosła się z 0ºV do 120ºC?
16. Oblicz temperaturę początkową wody o masie 1 kg, jeżeli po dostarczeniu jej 300 kJ ciepła jej
temperatura wzrosła do 95ºC.
17. W naczyniu znajduje się 500 g wody o temperaturze 20ºC. Dolano do niej 200 g wody o temperaturze
95ºC. Oblicz temperaturę wody po wymieszaniu.
18. Do naczynia z 800 g wody o temperaturze 5ºC dolano 600 g bardzo gorącej wody. Po chwili zmierzono
temperaturę wody – wynosiła 40ºC. Jaka była temperatura dolanej gorącej wody?
19. Kawałek żelaza o masie 0,2 kg i temperaturze 1200ºC wrzucono do wody o temperaturze 20ºC, w
wyniku czego woda ogrzała się do temperatury 90ºC. Jaka była masa wody?
20. Oblicz, jaką ilość ciepła należy dostarczyć kawałkowi lodu o masie 300 g w temperaturze 0ºC, aby
zamienił się w wodę o temperaturze 24ºC?
21. Dwa kilogramy wody o temperaturze 25ºC zostało oziębione i zamienione w lód o temperaturze 30ºC.Ile ciepła zostało oddane otoczeniu? Narysuj wykres zależności temperatury od ilości oddanego
ciepła.
22. Jaka ilość pary wodnej o temperaturze 100ºC zamieni się w wodę o tej samej temperaturze, jeżeli
oddane zostanie ciepło o wartości 6 MJ?
23. Ile pary wodnej o temperaturze 100ºC trzeba w[puścić do termosu zawierającego 2 kg wody o
temperaturze 15ºC, aby końcowa temperatura ustaliła się na poziomie 25ºC?
24. Para pewnej cieczy o masie 400 g w temperaturze skraplania zmienia się w ciecz o tej samej
temperaturze, oddając przy tym 116,8 kJ ciepła. Jakie jest ciepło parowania tej cieczy? Jaka to ciecz?
25. W mosiężnym kalorymetrze, którego masa jest równa0,7 kg, znajduje się lód o masie 0,2 kg. Całość ma
temperaturę 0ºC. Do kalorymetru wlano 600 g wody. Jaka powinna być jej temperatura, aby połowa
lodu uległa stopieniu?











