Model LONDONÓW Założenie: R=0 Z I równania dynamiki: gdzie: v

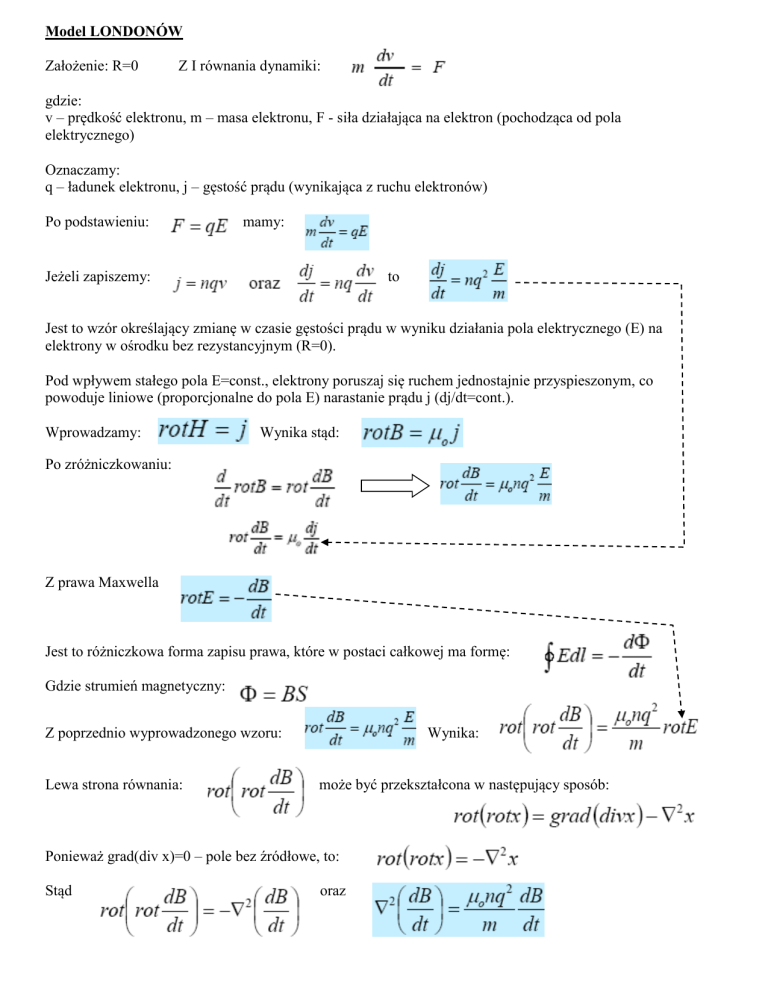
Model LONDONÓW
Założenie: R=0
Z I równania dynamiki:
gdzie:
v – prędkość elektronu, m – masa elektronu, F - siła działająca na elektron (pochodząca od pola
elektrycznego)
Oznaczamy:
q – ładunek elektronu, j – gęstość prądu (wynikająca z ruchu elektronów)
Po podstawieniu:
mamy:
Jeżeli zapiszemy:
to
Jest to wzór określający zmianę w czasie gęstości prądu w wyniku działania pola elektrycznego (E) na
elektrony w ośrodku bez rezystancyjnym (R=0).
Pod wpływem stałego pola E=const., elektrony poruszaj się ruchem jednostajnie przyspieszonym, co
powoduje liniowe (proporcjonalne do pola E) narastanie prądu j (dj/dt=cont.).
Wprowadzamy:
Wynika stąd:
Po zróżniczkowaniu:
Z prawa Maxwella
Jest to różniczkowa forma zapisu prawa, które w postaci całkowej ma formę:
Gdzie strumień magnetyczny:
Z poprzednio wyprowadzonego wzoru:
Lewa strona równania:
Wynika:
może być przekształcona w następujący sposób:
Ponieważ grad(div x)=0 – pole bez źródłowe, to:
Stąd
oraz
Wprowadzamy wielkość:
nazywaną Londonowską głębokością wnikania (wymiar metr)
Stąd
Równanie ma postać:
gdzie oznaczono
Równanie dotyczy pochodnej w czasie indukcji B tj. zmiennego w czasie pola magnetycznego. Po
scałkowaniu względem czasu otrzymujemy wniosek B=const.
Równanie to wykazuje, więc, że konsekwencją prawa Ohma i zerowego oporu (nieskończonego
przewodnictwa) jest tylko stała w czasie, wartość pola magnetycznego.
Założenie zerowej wartości oporu elektrycznego ośrodka, prowadzi do wniosku, że w ośrodku takim nie może
istnieć (poza powierzchnią) zmienne pole magnetyczne. Pochodna pola dB/dt, zanika w warstwie
powierzchniowej wg funkcji, eksponencjalnej.
Rozwiązanie równania
względem czasu daje w wyniku stałą w czasie wartość indukcji.
Rozkład przestrzenny pola magnetycznego w ogólnym przypadku jest opisany
wzorem:
Zerowy opór daje, więc w konsekwencji rozkład pola magnetycznego wewnątrz idealnego przewodnika w
postaci przebiegu malejącego ku osi.
Z doświadczenia wynika jednak, że pole to jest nie tylko stałe, ale równe zeru. Londonowie intuicyjnie
przyjęli rozwiązanie szczególne równania, a mianowicie rozwiązanie:
Oznacza to, że równanie uprzednio zapisane w odniesieniu do pochodnej w czasie indukcji B, dotyczy
również indukcji:
Rozwiązanie dla płaskiej granicy nadprzewodnik-próżnia.
Dla przypadku jednowymiarowego równanie Londonów ma postać:
Jest to równanie względem współrzędnej x..
Przyjmujemy, że dla x>0 mamy obszar jednorodnego,
nieskończonego nadprzewodnika. Pole magnetyczne jest
równoległe do powierzchni.
Rozwiązanie równania:
Zastępcza głębokość wnikania.
Wynik ten oznacza, że LGW jest zastępczą głębokością na której, strumień magnetyczny przy stałej indukcji
Ba :
ma taką samą wartość jak strumień przy rzeczywistym rozkładzie indukcji
B(x)=Ba exp(-x/ λL).
Kwantyzacja strumienia magnetycznego
Z mechaniki kwantowej wynika, że stany stacjonarne układów fizycznych są określone przez warunki
kwantowe.
Tezę taką przedstawił London zakładając, że: Strumień magnetyczny przechodzący przez nadprzewodzącą
pętlę nie może przyjmować dowolnych wartości.
Teza:
Wartość strumienia może być tylko wielokrotnością pojedynczej porcji - kwantu
strumienia.
Nośnikami ładunku w nadprzewodnikach są tzw. „pary Coopera”.
Układ dwóch związanych ze sobą – przyciągających się – elektronów.
Odległość elektronów pary - długość koherecji: ξ
Elektrony pary Coopera mają przeciwnie skierowane pędy i spiny. Wypadkowy pęd pary jest równy zeru.
Długość koherencji - przykłady:
Funkcja falowa elektronu
Mechanika kwantowa opisuje cząstkę za pomocą fali
Wykres fali
Dla t=t1 oraz t=t2 ruch fali elektronowej:
Gradient fazy (zmiana fazy) fali elektronowej na drodze od A do B:
Długość fali elektronowej
Pęd pary elektronowej w polu magnetycznym jest równy
Człon wynikający z ruchu elektronu w polu magnetycznym:
Stąd
Z wzoru:
otrzymuje się:
Dalsze przekształcenie:
Wyrażenie na prędkość elektronu:
Zmiana fazy fali pary elektronowej na drodze od A do B - wzór przekształcony
Całkowanie po drodze zamkniętej. Zmianę fazy na drodze zamkniętej:
Całkowita zmiana fazy na drodze zamkniętej (powrót do tego samego punktu)
k – liczba całkowita
Warunek istnienia na obwodzie całkowitej liczby fal
To
Dla drogi całkowania położonej dostatecznie daleko od krawędzi otworu
oraz
Z teorii pola magnetycznego
Całka powierzchniowa z indukcji jest równa strumieniowi magnetycznemu przenikającemu przez
powierzchnię s.
Dla k=1 (jeden obieg linii całkowania)
Jest to najmniejsza porcja strumienia magnetycznego tzw. Kwant strumienia (flukson)
Kwanty strumienia magnetycznego (fluksony) występują zawsze, gdy pole magnetyczne przenika przez
nadprzewodnik. Zjawisko kwantowania strumienia odgrywa zasadniczą rolę w tzw. nadprzewodnikach II
rodzaju, do których strumień magnetyczny wnika w postaci kwantów lub „pęków” kwantów.
Wszystkie pary Coopera znajdują się w identycznych stanach, są skorelowane ze sobą. Wynika stąd, że
zgodne są ich fazy. W przypadku zmiany strumienia przenikającego przez pierścień o jeden kwant, faza par
Coopera zmienia się o