Mikroprocesory i procesory sygnałowe

Mikroprocesory i procesory
sygnałowe
cz. I – Procesory „klasyczne”






Historia procesorów, porównanie procesorów CISC i RISC
Model programowy procesorów Intel x86.
Koprocesor.
Rozszerzenia MMX, SIMD
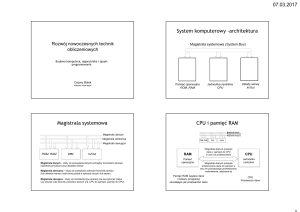
Architektury von Neumanna, Harvard
Rodziny procesorów: VLIW, EPIC, ARM, PowerPC, MIPS
cz. II – Procesory sygnałowe




Jednostki obliczeniowe stało- i zmiennoprzecinkowe
Specjalizowane jednostki MAC, SHIFTER, DAG
Mechanizmy programowe procesora DSP, konstrukcja
podstawowych algorytmów, optymalizacja kodu
Typowe algorytmy przetwarzania sygnałów:

 Budowa
Transformata Fouriera, Filtry cyfrowe, Zagadnienia sztucznej inteligencji
i elementy składowe systemu mikroprocesorowego.
1
Warunki uzyskania zaliczenia:

Obecność na ćwiczeniach (maksymalnie 2
nieusprawiedliwione nieobecności)

Pozytywna ocena z ćwiczeń (w tym 2 prace
kontrolne)

Obecność na laboratoriach i wykonanie pełnego
zestawu ćwiczeń (sprawozdania oceniane
indywidualnie).
2
Literatura i materiały:










G.Syck, Turbo Assembler. Biblia Użytkownika, LT&P, Warszawa 1994
J.Scanlon, Assembler 80286/80386
J.Biernat, Architektura komputerów, Oficyna Wydawnicza Politechniki
Wrocławskiej, Wrocław, 1999
J.Grabowski, S. Koślarz, Podstawy i praktyka programowania
mikroprocesorów, WNT, Warszawa, 1987
A. Niederliński, Mikroprocesory, mikrokomputery, mikrosystemy,
Wydawnictwa Szkolne i Pedagogiczne, Warszawa, 1991
P.Metzger, Anatomia PC, Helion
C.Marven,G.Ewers, Zarys cyfrowego przetwarzania Sygnałów, WKŁ,
Warszawa, 1999
Czasopisma specjalistyczne i popularnonaukowe
Podręczniki i materiały firmowe („Data Sheets”, „Programming
Manuals”, „Application Notes”) do omawianych procesorów
Książki dotyczące podstaw cyfrowego przetwarzania sygnałów –
wybrane rozdziały
3
Wykład 1
Przetwarzanie sygnałów analogowych
przez system cyfrowy
Y-Axis
Y-Axis
CPU
t[s]
X-Axis
4
Cyfrowa reprezentacja
sygnałów analogowych:
systemy liczenia: binarny i szesnastkowy
liczby rzeczywiste stałoprzecinkowe
i zmiennoprzecinkowe
podstawowe operacje arytmetyczno-logiczne
procesorów
System dziesiętny
Cyfry mogą przyjmować dziesięć różnych wartości:
0,1..9
2*1 + 1*10 = 2*100 + 1*101 + 0*102 + ...
2*100 + 1*101 + 0*102 + ... = 12
12 =
012 =
System binarny
Cyfry mogą przyjmować tylko jedną z dwóch wartości:
0 lub 1
1100b =
0*20
0*1
+ 0*21
+ 0*2
+ 1*22 + 1*23 + ... =
+ 0*4 + 0*8
= 12 (dec)
numer bitu
7
6
5
4
3
2
1
0
wartość
27
26
25
24
23
22
21
20
128 64
32
16
8
4
2
1
j.w.
Tabela 1. Wartości (wagi) bitów w zapisie binarnym
System binarny
Minimalna liczba w zapisie binarnym dla słowa 4bitowego wynosi:
0000b =
0*20
+ 0*21
+ 0*22 + 0*23 = 0 (dec)
... natomiast maksymalna:
1111b =
1*20 + 1*21 + 1*22 + 1*23 =
1*1
+ 1*2
+ 1*4 + 1*8
= 15 (dec)
Dla słów 8 bitowych (bajtów) zakres ten wynosi
odpowiednio:
minimum : 00000000b = 0
maksimum: 11111111b = 255
Zapis liczb ujemnych – system
uzupełnień do jedynki (U1)
LICZBY UJEMNE MAJĄ ZAMIENIONE WSZYSTKIE BITY NA PRZECIWNE
00001100b = +12
11110011b = -12
najbardziej znaczący bit (pierwszy z lewej) oznacza
znak liczby: 0 –liczba dodatnia, 1 – liczba ujemna
Uwaga 1: Liczba zero może mieć znak !
00000000b = +0
11111111b = -0
Uwaga 2:
Zakres liczb ulega zmianie z
0..255 na -127...-0,+0,...+127
Zapis liczb ujemnych – system
uzupełnien do dwóch (U2)
LICZBĘ UJEMNĄ ZAPISUJE SIĘ W SYSTEMIE U2 ZAPISUJĄC JEJ
WARTOŚĆ BEZWZGLĘDNĄ W POSTACI BINARNEJ, PO CZYM
ZAMIENIAJĄC WSZYSTKIE BITY NA PRZECIWNE (U1) ORAZ
DODAJĄC LICZBĘ „1”
przykład: zapis liczby –12 w systemie U2:
• zapis binarny wartości bezwzględnej liczby (bez
znaku)
• zamiana wszystkich bitów na przeciwne (U1)
• dodanie liczby 1 (00000001b)
1
2
3
+12 (dec) = 00001100b
11110011b
+00000001b
==========
11110100b
= -12
Specjalny wskaźnik N (Negacji) zostanie ustawiony N=1
(jest to kopia bitu 7 wyniku)
Zapis liczb ujemnych – system
uzupełnien do dwóch (U2)
... i odwrotnie: WARTOŚĆ BEZWZGLĘDNĄ LICZBY UJEMNEJ OBLICZA
SIĘ ZAMIENIAJĄC WSZYSTKIE BITY NA PRZECIWNE (U1) A
NASTEPNIE DODAJĄC LICZBĘ „1”
1.
2.
3.
11110100b
00001011b
+00000001b
==========
00001100b
= -12
=
+12
Sprawdzenie czy +12 + (-12) = 0 ???
+12 (dec) = 00001100b
-12 (dec) = 11110100b
+ =====================
1 00000000b = 0 !!! wskaźnik C=1 (Carry)
Uwaga ! System ten jest najczęściej używany w praktyce ze
względu na prostotę przeprowadzania operacji
arytmetycznych.
Zapis liczb ujemnych –
zastosowanie przesunięcia
zakresu (offsetu)
Umowny podział zakresu zmienności 0..255 na dwa
podzakresy poprzez zastosowanie tzw. offsetu równego
zazwyczaj połowie zakresu zmienności liczby binarnej
wartość liczby ze znakiem (-127...+128) =
wartość binarna (0..255) – offset(127)
Zapis taki stosowany jest
w komputerach PC, oraz w
systemach.
np. przez
niektórych
koprocesor
prostszych
System szesnastkowy
(hexadecymalny)
Cyfry mogą przyjmować tylko jedną z szesnastu
postaci:
0,1,... 8, 9, A, B, C, D, E, F
odpowiadających wartościom
0,1,... 8, 9,10,11,12,13,14,15
i tak np. liczba szesnastkowa 0Ch odpowiada liczbie
dziesiętnej 12
numer cyfry
3
wartość
163
j.w.
2
1
0
162 161 160
4096 256 16
1
Tabela 2. Wagi cyfr systemu szesnastkowego
System szesnastkowy
Inny przykład:
1278h = 1*4096 + 2*256 + 7*16 + 8*1 = 4728
Uwaga 1 Liczby szesnastkowe mogą być oznaczane również
przez 0x1278 lub $1278
Uwaga 2 Zapis szesnastkowy używany jest tylko dla
wygody prezentacji liczb binarnych !!!
Każda z cyfr liczby szesnastkowej składa się z 4 bitów
(cyfr szesnastkowych). Wygodnie jest więc zapisując
liczby binarne stosować odstępy (spacje) pomiędzy
grupami 4 bitów, np.
+12 (dec) = 00001100b == 0000 1100b = 0Ch
-12 (dec) = 11110100b == 1111 0100b = F4h
Dla większych liczb, np. 16-bitowych korzyść z takiego
zapisu jest od razu widoczna
0100110011111100b == 0100 1100 1111 1100b = 4CFCh
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
1
Liczby całkowite, ze znakiem (U2) i bez znaku
dodawanie (ADD)
przykład:
mov EAX,10
add EAX,20
;wpisanie do rejestru EAX liczby 10
;dodanie do zawartość EAX liczby 20
;(EAX:=EAX+20) C=0
dodawanie z przeniesieniem (ADC)
W=A+B+C
(C=0 lub 1)
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
2
odejmowanie (SUB)
mov EAX,10
sub EAX,20
;wpisanie do rejestru EAX liczby 10
;odjęcie od zawartość EAX liczby 20
(w tym przypadku wynik będzie ujemny (N=1), oraz
nastąpi pożyczka (C=1))
odejmowanie z pożyczką (SBB)
W=A-B-C
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
3
inwersja bitów (NOT)
- tak jak w systemie uzupełnień do jedynki U1
mov EAX,12 ;wpisanie do rejestru EAX liczby 12
NOT EAX
negacja liczby (NEG)
– system uzupełnień do dwóch (U2)
mov EAX,12
NEG EAX
W=(NOT A) +1
;wpisanie do rejestru EAX liczby 12
;w EAX jest –12 (U2)
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
4
mnożenie liczb (MUL) :
- wynik ma dwa razy więcej bitów niż składniki
mnożenia (wynik zawsze w DX:AX)
mov ax,2000h
mov bx,10h
mul bx
po wykonaniu mnożenia w rejestrze DX znajdzie się
liczba 2h, a w AX liczba 0000h (łączny wynik 20000h)
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
5
dzielenie liczb (DIV) :
dzielna w DX:AX
wynik w postaci: część całkowita (AX) i reszta (DX)
mov
mov
mov
div
dx,3h
ax,205h
bx,100h
bx
;AX = 302h = (30205h/100h)
;DX = 5 (reszta z dzielenia)
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
6
Iloczyn logiczny (AND) :
mov dx,11000011b
and dx,11110000b
;w dx będzie
11000000b
A
B
W
AND
0
1
0
0
0
0
0
1
0
1
1
1
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
7
Suma logiczna (OR) :
mov ax,11000011b
or ax,11110000b
;w ax będzie
11110011b
A
B
W
0
0
0
OR
1
0
1
0
1
1
1
1
1
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
8
Funkcja EXOR:
mov ax,11000011b
exor ax,11110000b
;w ax będzie
00110011b
A
B
W
XOR
0
1
0
0
0
1
0
1
1
1
1
0
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
Przesuwanie bitów
logiczne:
SHR,SHL:
Arytmetyczne:
SAR,SAL:
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
Przesuwanie bitów: ROR,ROL
Podstawowe operacje
arytmetyczno-logiczne mikroprocesorów
Przesuwanie bitów:ROR,ROL - przykład
;wartość początkowa „C” bez znaczenia
mov
ror
ax,11000011b
ax,1
11100001b
;po wykonaniu C=1
;przesunięcie o trzy pola
mov ax,11000011b
ror ax,3
01111000b
;po wykonaniu C=0