Optyka falowa - mlewandowska.zut.edu.pl

Optyka falowa – zjawiska dyfrakcji i interferencji światła (rozdz. 36.1-36.7, 37.1-37.2,
37.7-37.8)
Efektowne barwy baniek mydlanych, lub wycieków oleju w kałużach są wynikiem
interferencji światła. Jak mówiliśmy, interferencja polega na selektywnym wzmacnianiu lub
wygaszaniu nakładających się fal. Jeśli nakładające się fale mają zgodne fazy
(   0  2n ), następuje maksymalne wzmocnienie fali wypadkowej, natomiast
interferencja fal o przeciwnych fazach (     2n ) prowadzi do ich całkowitego
wygaszenia. Zjawisko interferencji światła, a także zjawisko dyfrakcji, czyli ugięcia fal
świetlnych, są najsilniejszymi dowodami na falową naturę światła. Aby zrozumieć i opisać te
zjawiska musimy wyjść poza ograniczenia optyki geometrycznej.
Zasada Huygensa
Pierwszą stosunkowo prostą i użyteczną falową teorię światła zaproponował w XVII
w. Christian Huygens. Teoria Huygensa pozwala w prosty sposób przewidywać rozchodzenie
się dowolnego rodzaju fal, a więc także fal świetlnych, w przestrzeni trójwymiarowej. Opiera
się ona na zasadzie Hugensa, która mówi, że wszystkie punkty czoła fali zachowują się jak
punktowe źródła elementarnych kulistych fal wtórnych. Po upływie czasu t położenie
czoła fali jest wyznaczone przez powierzchnię styczną do powierzchni fal wtórnych.
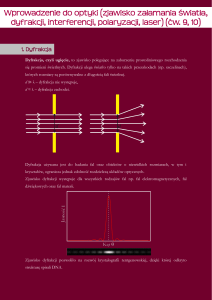
Rys. 1 Rozchodzenie się fali płaskiej w ośrodku jednorodnym. Na rysunku zaznaczono 3
punktowe źródła elementarnych fal kulistych wtórnych na czole fali płaskiej w chwili
początkowej t0 oraz położenia powierzchni fal wtórnych po upływie pewnego czasu t. Styczna
do powierzchni fal wtórnych wyznacza czoło fali w chwili t0+t. Czoło to jest linia prostą, co
jest charakterystyczne dla fali płaskiej.
Korzystając z zasady Huygensa można wyprowadzić empiryczne prawo załamania
(zad.+spr.1), a także wniosek, że długość fali świetlnej  n w ośrodku materialnym zależy od
współczynnika załamania n tego ośrodka

v
n   
(1)
n
c
gdzie  jest długością fali świetlnej w próżni. Natomiast częstość światła w ośrodku
materialnym jest taka sama jak w próżni
v
c/n c
fn 

  f
(2)
n  / n 
a więc kiedy fala świetlna wchodzi do innego ośrodka jej barwa nie ulega zmianie.
Z równania (1) wynika ważny wniosek: różnica faz pomiędzy dwiema falami może ulec
zmianie, jeśli fale te rozchodzą się w dwóch ośrodkach o różnych współczynnikach
1
załamania. Taka zmiana różnicy faz może być odpowiedzialna za efekty interferencji w
określonym punkcie ośrodka (rys. 2)
Rys.2 Dwie fale rozchodzące się w ośrodku o współczynniku
załamania n1 mają początkowo zgodne fazy. Fala 2 przechodzi
przez warstwę ośrodka o współczynniku załamania n2>n1.
Długość fali w warstwie ulega skróceniu. Na skutek tego po
wyjściu z warstwy fazy fal są przeciwne.
1
Przykład (zad. 1)
Żółte światło lampy sodowej ma w powietrzu długość fali 589 nm. a) Ile wynosi jego częstość
b) Ile wynosi długość fali tego światła w szkle o współczynniku załamania 1,5? c) Oblicz
prędkość rozchodzenia się tego światła w szkle
Zakładamy, że współczynnik załamania powietrza wynosi 1 (w rzeczywistości 1.00029),
a prędkość rozchodzenia się światła w powietrzu wynosi c=3e8 m/s
a) cT=c/f
f=c/=5.09e14 Hz
b) Korzystamy ze wzoru (1) n=/n=392.6 nm
c) Korzystamy np. z definicji współczynnika załamania n=c/v v=c/n=2e8 m/s
Pojęcie dyfrakcji
Istota zjawiska dyfrakcji polega na tym, że fala napotykająca na swojej drodze przeszkodę np.
przesłonę, w której znajduje się szczelina, albo ostrą krawędź, ulega ugięciu (dyfrakcji) w
całym obszarze za przeszkodą. Rozprzestrzenianie się fal za przeszkodą można analizować w
oparciu o zasadę Huygensa (rys.). Dyfrakcji ulegają fale wszystkich rodzajów, a jej efekty są
wyraźne, gdy rozmiary szczeliny są rzędu długości fali. Im węższa jest szczelina, tym
silniejsze ugięcie fali, dlatego też nie można uzyskać promienia światła przepuszczając
światło przez wąską szczelinę.
Doświadczenie interferencyjne Younga
W 1801 r. Thomas Young wykonał doświadczenie stanowiące dowód na to, że światło
ma charakter falowy, co było sprzeczne z poglądami większości ówczesnych uczonych.
Schemat doświadczenia Younga jest następujący: światło monochromatyczne, przepuszczone
zostaje przez szczelinę S0 ulegając dyfrakcji, następnie kierowane jest na przesłonę z dwiema
szczelinami S1 i S2. W wyniku ugięcia światła na tych szczelinach powstają dwie fale koliste,
które interferują ze sobą. Na umieszczonym dalej ekranie obserwujemy obraz złożony z
jasnych i ciemnych prążków interferencyjnych.
Jasne prążki powstają na skutek wzmocnienia interferencyjnego (środki jasnych prążków
odpowiadają maksimom interferencji), natomiast ciemne prążki są wynikiem interferencji
destruktywnej, czyli wygaszania (środki ciemnych prążków odpowiadają minimom
interferencji).
W chwili przechodzenia przez szczeliny obie fale świetlne maja tę samą fazę, gdyż są one
częściami tej samej fali padającej. Jednak po przejściu przez szczeliny każda z fal składowych
przebywa inną drogę, aby osiągnąć dowolny punkt P na ekranie. Powoduje to, że fale
składowe docierające do punktu P mogą mieć różne fazy.
2
Różnica dróg L przebytych przez fale składowe powoduje różnicę ich faz w punkcie P.
Różnica faz fal składowych decyduje o natężeniu światła w punkcie P.
Jeśli różnica dróg jest równa całkowitej wielokrotności długości fali
L  0  m
(3a)
wówczas w takim punkcie fazy fal składowych są zgodne i występuje maksimum
interferencyjne, a więc natężenie światła jest maksymalne. Jeśli natomiast różnica dróg
spełnia warunek
(3b)
L   / 2  m
wówczas w takim punkcie fazy fal składowych są przeciwne i natężenie światła jest
minimalne.
Położenie jasnych i ciemnych prążków na ekranie możemy jednoznacznie określić za
pomocą kąta  względem osi układu. Obliczymy, jakie wartości kąta  odpowiadają
maksimom i minimom interferencyjnym. Obliczenia znacznie upraszczają się, gdy założymy,
że odległość ekranu od szczelin jest znacznie większa od odległości pomiędzy obiema
szczelinami (l>>d). Wówczas możemy w przybliżeniu traktować promienie r1 i r2 jako
wzajemnie równoległe, tworzące kąt  z osią układu (rys). Przy takich założeniach
otrzymujemy związek
(4)
L  d sin 
Porównując równanie (4) z warunkami (3a) i (3b) otrzymujemy położenie prążków na
ekranie. Położenie środka jasnego prążka m-tego rzędu określa równanie
(5a)
d sin   m , gdzie m  0, 1, 2 ...
np. dla m=0 jasny prążek znajduje się pod kątem =0, a więc na osi (maksimum centralne)
Położenie środków ciemnych prążków określa warunek

d sin    m 

1
 , gdzie m  0, 1, 2 ...
2
(5b)
Przykład (zad.13)
Doświadczenie Younga wykonywane jest z użyciem światła zielonego o długości fali 550 nm.
Odległość między szczelinami jest równa 1,2 mm, a ekran na którym powstaje obraz, jest
odległy od szczelin o 5,4 m. Oblicz odległość pomiędzy jasnymi prążkami.
Korzystając ze wzoru (5a) obliczamy położenia środków kolejnych prążków:
Prążek centralny (m=0) =0 y=0
Prążki I rzędu (m=1) sin=/d=0.000458 tg=0.000458 y=ltg=0.00247m=2.47 mm
Prążki II rzędu (m=2) sin=2/d=0.000917 tg=0.000917 y=ltg=0.00495m=4.95 mm
y=2.47mm
Spójność światła
Warunkiem dostrzegalnej interferencji dwóch fal świetlnych spotykających się w jednym
punkcie jest ich spójność (koherencja), co oznacza, że różnice faz fal składowych muszą być
stałe w czasie. Źródłami światła spójnego są lasery. W doświadczeniu Younga można
stosować źródło światła częściowo spójnego, w którym fale świetlne mają stałą różnicę faz w
punktach, leżących blisko siebie (np. światło słoneczne), ale należy przepuścić je najpierw
przez pojedynczą szczelinę. Światło wychodzące z wąskiej szczeliny S0 jest spójne, a
ponadto, na skutek ugięcia, może oświetlić obie szczeliny S1 i S2. Jeśli zamiast układu dwóch
szczelin użylibyśmy dwóch źródeł światła monochromatycznego o podobnej wielkości prążki
interferencyjne nie pojawią się i ekran oświetlony będzie równomiernie.
3
Interferencja światła w cienkich warstwach
Rozważmy światło monochromatyczne o długości  padające pod katem  na cienką
przezroczystą warstwę o grubości L i współczynniku załamania n2 > n1 (rys.). Na granicy
ośrodków w punkcie A światło ulega zarówno odbiciu, jak i załamaniu. Promień odbity
oznaczony symbolem r1 biegnie do obserwatora. Promień załamany ulega odbiciu od dolnej
powierzchni warstwy w punkcie B, a następnie odbiciu i załamaniu na górnej powierzchni
warstwy w punkcie C. Promień załamany wychodzący z warstwy, oznaczony symbolem r2,
dociera do obserwatora. Przeprowadzimy uproszczona analizę zagadnienia dla przypadku
małych kątów padania (   0 0 )
Jeśli fale świetlne, reprezentowane przez promienie i r2, interferujące ze sobą w oku
obserwatora mają zgodne fazy, wówczas obszar AC na powierzchni warstwy ma dla
obserwatora maksymalną jasność. Jeśli natomiast ich fazy są przeciwne, wówczas obszar AC
z punktu widzenia obserwatora będzie ciemny, pomimo że jest on jasno oświetlony! Jeśli
różnica faz obu fal ma wartość pośrednią, wtedy jasność obszaru AC również jest pośrednia.
Różnica faz fal reprezentowanych przez promienie r1 i r2, wynika z 3 przyczyn:
1. Odbicie
2. Różnica dróg przebytych przez obie fale
3. Przechodzenie fal przez ośrodki o różnych współczynnikach załamania
Ad. 1. Odbicie od ośrodka o większym współczynniku załamania powoduje zmianę fazy fali
świetlnej na przeciwną, co odpowiada ½ długości fali, odbicie od ośrodka o mniejszym
współczynniku załamania nie zmienia fazy fali świetlnej. Fala reprezentowana przez
promień r1 odbijając się w punkcie A zmienia fazę na przeciwną, natomiast odbicie od
dolnej powierzchni warstwy w punkcie B nie zmienia fazy fali związanej z promieniem r2.
Ad. 2. Droga promienia r2 jest dłuższa ze względu na dwukrotne przejście przez warstwę. Dla
małych kątów padania   0 0 różnica dróg przebytych przez obie fale wynosi w
przybliżeniu 2L
Ad. 3. Zgodnie z równaniem (1) długość fali związanej z promieniem r2 wewnątrz warstwy
wynosi /n2.
Podsumowując:
Minimum interferencyjne (ciemny obszar AC) odpowiada sytuacji gdy

2 L  m , gdzie m  1, 2 ...
(6a)
n2
Natomiast maksimum interferencyjne (jasny obszar AC) określa warunek
1 

(6b)
2 L   m   , gdzie m  0, 1, 2 ...
2  n2

A więc skutek interferencji będzie zależał od cech warstwy (jej grubości oraz współczynnika
załamania) oraz od długości fali padającego światła.
Z całkiem wyjątkową sytuacja mamy do czynienia wtedy, gdy L   . W takim
przypadku różnica faz miedzy falami r1 i r2, wywołana jest jedynie przez odbicie, zatem
niezależnie od długości fali padającego światła następuje interferencja destruktywna i
warstwa pozostaje ciemna.
Jeśli natomiast wiązka padającego światła zawiera różne długości fali (np., gdy jest to
światło białe) następuje selektywne wygaszanie i wzmacnianie niektórych długości fali,
wówczas odcień powierzchni warstwy zmienia się wraz z kierunkiem jej oglądania
(opalizuje). Tego rodzaju efekt możemy zauważyć obserwując skrzydła motyla, bańki
mydlane lub rozlane plamy oleju.
Siatka dyfrakcyjna
4
Siatka dyfrakcyjna jest układem bardzo wielu N jednakowych, równoodległych
szczelin (siatka transmisyjna) lub rys na zwierciadle metalicznym (siatka odbiciowa).
Odległość d środków sąsiednich szczelin (lub rys) nazywamy stałą siatki. Typowa siatka
dyfrakcyjna dla promieniowania z zakresu nadfioletu ma ok. 1000 szczelin/mm
(d=0.001mm), zaś dla podczerwieni do 300 szczelin/mm (d=0.0033 mm). Oświetlając siatkę
dyfrakcyjną światłem monochromatycznym otrzymujemy na ekranie bardzo wąskie jasne
linie rozdzielone stosunkowo szerokimi ciemnymi obszarami.
Rysunek przedstawia uproszczona siatkę dyfrakcyjną, złożoną z N=5 równoodległych
szczelin. Do wyznaczenia położeń jasnych linii na ekranie wykorzystamy tę samą procedurę
co w przypadku doświadczenia Younga. Zakładamy więc, że ekran znajduje się dostatecznie
daleko od siatki (d>>l), tak że promienie wychodzące ze szczelin można traktować jako
równolegle. Dla każdej pary promieni wychodzących z sąsiednich szczelin obserwujemy
wzmocnienie, gdy różnica ich dróg jest równa całkowitej wielokrotności długości fali, a więc
(7)
L  d sin   m , gdzie m  0, 1, 2 ...
Czyli położenie linii określa warunek
(7a)
sin   m / d , gdzie m  0, 1, 2 ...
Każda liczba m odpowiada innej linii, dlatego też może być używana do numerowania linii –
liczby m nazywamy rzędem linii, mówimy na przykład linia zerowego rzędu (m=0 - linia
centralna, linia pierwszego rzędu (m=1) itd.
W przypadku siatki dyfrakcyjnej linie są bardzo wąskie, ze względu na to, że powstają
w wyniku konstruktywnej interferencji bardzo dużej liczby fal składowych. Ze względu na
małą wartość stałych siatki odległości kątowe pomiędzy poszczególnymi liniami są znacznie
większe niż w doświadczeniu Younga z 2 szczelinami.
Ze wzoru (7) wynika, ze dla danej siatki położenie kątowe każdej linii zależy od
długości fali światła padającego. Dlatego też, jeśli na siatkę pada światło o nieznanej długości
fali, to pomiar kątów  dla linii wyższych rzędów powala wyznaczyć długość fali tego
światła. Jeśli światło padające zawiera kilka różnych długości fali, linie odpowiadające
różnym długościom fali mogą być na tyle dobrze rozseparowane, że można je rozróżnić i
zidentyfikować. Z tego powodu siatki dyfrakcyjne są wykorzystywane (podobnie jak
pryzmaty) do budowy spektroskopów optycznych, wykorzystywanych w analizie widmowej.
Zdolność rozdzielcza siatki dyfrakcyjnej, czyli jej zdolność do rozdzielania linii o
różnych długościach fali zależy od szerokości linii. Obliczymy teraz szerokość linii
centralnej. W tym celu poszukamy położenia pierwszego minimum, w którym N promieni
wychodzących ze szczelin wygasza się całkowicie. Pierwsze minimum powstaje w miejscu,
gdzie różnica dróg między skrajnymi jest równa (wtedy skrajny dolny promień oraz
promień środkowy wygaszają się, podobnie wygaszają się kolejne pary wyższych promieni).
Jak widać na rysunku, dla siatki składającej się z N szczelin odległych od siebie o d pierwsze
minimum powstaje w miejscu, gdzie spełniony jest warunek
L  Nd sin  1 / 2  
(8)
A więc szerokość połówkowa linii centralnej wynosi
 1 / 2  sin  1 / 2   /( Nd )
(9)
(Zastosowaliśmy przy tym przybliżenie  1 / 2  sin  1 / 2 ponieważ  1 / 2 jest bardzo małe).
Oczywiście całkowita szerokość linii jest równa 2 1 / 2 .
Można też udowodnić, że szerokość połówkowa linii wyższego rzędu zależy od jej położenia
kątowego i wynosi
 1 / 2   /( Nd cos )
(10)
Jak widać, dla danej długości fali l i zadanej stałej siatki d szerokość linii maleje wraz ze
wzrostem liczby szczelin N. Zatem siatka o większej liczbie szczelin, wytwarzająca węższe (a
5
więc słabiej nakładające się) linie będzie lepiej rozdzielała linie różniące się długością fali,
zatem będzie miała większą zdolność rozdzielczą.
Regularnie uszeregowane atomy w krysztale stanowią trójwymiarową siatkę
dyfrakcyjną dla promieniowania elektromagnetycznego o małych długościach fali (np.
promieniowanie rentgenowskie). Dzięki temu dyfrakcja promieniowania rentgenowskiego
jest jednym z podstawowych narzędzi do badania rozmieszczenia atomów w strukturach
krystalicznych.
Przykład
W żółtym świetle lampy sodowej występują dwie linie (zwane dubletem sodowym) o niewiele różniących się
długościach fali 589 nm i 589,59 nm. Siatkę dyfrakcyjną mającą 12500 równoodległych szczelin na
odcinku 2,5 cm oświetlono lampą sodową. Oblicz położenie kątowe oraz położenie na ekranie maksimum
pierwszego i drugiego rzędu dla obu długości fali. Czy linie te dadzą się rozróżnić? Ekran znajduje się w
odległości 2m od siatki.
Obliczamy stałą siatki d= 0.025m/12500=2*10-6m
Dla widma I rzędu
sin1=1/d=0.29451=17,1276o tg1=0.3082 y1=l tg1=0.6163 m=61,63 cm
sin2=2/d=0.294795 2=17,1452o tg2=0.3085 y2=l tg2=0.6170 m=61,70 cm
 1 / 2   /( Nd cos  1 )  2,47  10 5 rad = 0.0014o
y=0.7 mm
Dla widma II rzędu
sin1=21/d=0.5891=36,0861o tg1=0.7288 y1=l tg1=1,4577 m=145,77 cm
sin2=22/d=0.58959 2=36,1279o tg2=0.7300 y2=l tg1=1,4599 m=145,99 cm
y=2,2 mm
 1 / 2   /( Nd cos  1 )  2,92  10 5 rad = 0.0017o
Linie dubletu sodowego powinny się dać rozróżnić za pomocą tej siatki.
Jak widać odległości między liniami wzrastają dla wyższych rzędów (Jednocześnie jednak
linie wyższych rzędów stają się słabsze i szersze)
6