Natura światła
W XVII wieku ścierały się dwa, poglądy na temat natury światła.
1. Isaac Newton twierdził Ŝe światło składa się z bardzo szybko poruszających się korpuskuł
(cząstek). Załamanie światła tłumaczył Newton tym, Ŝe na cząstki światła działa siła
pochodząca od materii i działająca tylko w jej sąsiedztwie). ZauwaŜył teŜ, Ŝe promień światła
białego rozszczepia się po przejściu przez pryzmat na promienie o róŜnych kolorach.
2. Natomiast Christiaan Huygens twierdził, Ŝe światło jest falą. W 1678 roku sformułował,
nazwaną później jego nazwiskiem, zasadę Huygensa :
„ KaŜdy punkt ośrodka, do którego dotrze fala,
staje się źródłem nowej fali cząstkowej (kulistej
w przestrzeni i kolistej na płaszczyźnie)”.
Gdy fala dotrze do szczeliny, kaŜdy punkt ośrodka leŜący
wewnątrz niej staje się źródłem nowej fali.
Zasada ta dotyczy równieŜ fal mechanicznych
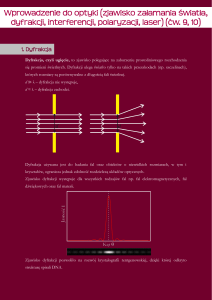
Dyfrakcja i interferencja fal
Jak wyjaśnić obraz fali po przejściu przez zespół szczelin?
Interferencja = nakładanie się fal
W punkcie P sumują się:
- dla fal mechanicznych wartości wychyleń cząstek z połoŜeń równowagi.
- dla fal EM wektory natęŜenia pola elektrycznego i indukcji magnetycznej.
Doświadczenie Younga
asinα = nλ
Z2
Interferometr Michelsona
B
Światło monochromatyczne ze źródła pada na
posrebrzone półprzepuszczalne lustro P.
Połowa wiązki świetlnej (A) jest przepuszczana
przez P a połowa (B) odbita. Obie wiązki po
odbiciu od zwierciadeł Z1 i Z2 i przejściu lub
odbiciu od P poruszają się w stronę detektora
(na rysunku jest nim oko ludzkie). JeŜeli drogi
promieni A i B są takie same lub róŜnią się o
całkowitą długość fali promienie interferują
konstruktywnie.
P
A
Z1
B A
Dyfrakcja od szczeliny
asinα = λ
Siatka dyfrakcyjna
d - stała siatki
asinΘ= nλ
Zdolność rozdzielcza przyrządów optycznych a dyfrakcja
S1
Θ
S2
Θ
P2
P1
Dyfrakcja promieni rentgenowskich
d - odległość między płaszczyznami
atomowymi kryształu
Warunek Bragga
2dsinΘ = nλ
Jeszcze jeden dowód na to, Ŝe światło jest falą:
Polaryzacja fal
Światło jest falą poprzeczną
E
v
Naturalne (spontanicznie promieniowane
0
przez atomy) światło jest mieszaniną fal
B
spolaryzowanych w róŜnych kierunkach
Z wiązki światła naturalnego moŜemy uzyskać wiązkę spolaryzowaną
przepuszczając ją przez polaryzator
A jednak światło to strumień cząstek!
Zjawisko fotoelektryczne
Aby elektron mógł opuścić metal naleŜy dostarczyć
mu pewną minimalną wartość energii którą nazywamy
pracą wyjścia. Energia ta moŜe być uzyskana np. poprzez absorpcję energii fali
elektromagnetycznej. Dla metali wartość pracy wyjścia wynosi 2−
−4 eV.
–
Elektrony emitowane są jedynie pod wpływem
„oświetlenia” falą o częstotliwości większej od
częstotliwości granicznej fotoefektu ν > ν gr
Równanie Einsteina
Oświetlanie metalu światłem o energiach fotonów E=hν >W umoŜliwia
elektronowi opuszczenie metalu
Promieniowanie rentgenowskie
Istnienie krótkofalowej granicy promieniowania
rentgenowskiego,
dla
danego
napięcia
przyspieszającego jest jednym z dowodów na
to, Ŝe promieniowanie elektromagnetyczne
(nie tylko światło widzialne) moŜna traktować
jako strumień cząstek (kwantów) - fotonów
Efekt Comptona
Równanie Comptona
∆λ = λ − λ0
Fotony - kwanty energii pola elektromagnetycznego
Istnieją fotony o dowolnie małych energiach!
m0f = mf 1 − (c / c ) 2 = 0
Foton jest cząstką bezmasową (jego masa spoczynkowa wynosi zero)!
Pęd fotonu
hν h
pf = mf c =
=
c λ
Dualizm falowo-cząstkowy fali elektromagnetycznej.
• W zjawiskach takich jak efekt Comptona czy efekt fotoelektryczny fala
elektromagnetyczna wykazuje naturę korpuskularną, tzn. jest strumieniem
cząstek zwanych fotonami.
• W zjawiskach takich jak dyfrakcja, interferencja czy polaryzacja fala
elektromagnetyczna wykazuje typowe własności falowe.