Wykład 1 1. Plazmon A - polaryton

Wykład 1
1. Plazmon
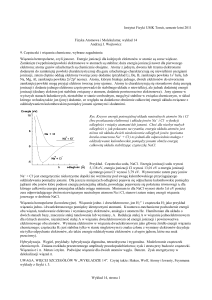
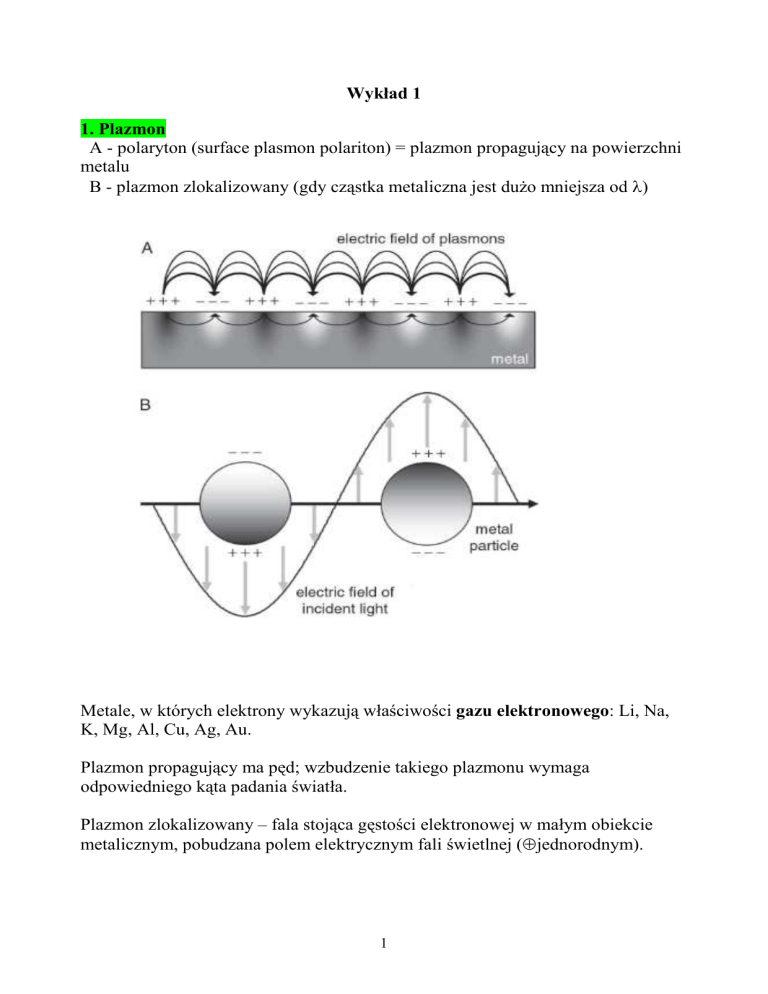
A - polaryton (surface plasmon polariton) = plazmon propagujący na powierzchni
metalu
B - plazmon zlokalizowany (gdy cząstka metaliczna jest dużo mniejsza od λ)
Metale, w których elektrony wykazują właściwości gazu elektronowego: Li, Na,
K, Mg, Al, Cu, Ag, Au.
Plazmon propagujący ma pęd; wzbudzenie takiego plazmonu wymaga
odpowiedniego kąta padania światła.
Plazmon zlokalizowany – fala stojąca gęstości elektronowej w małym obiekcie
metalicznym, pobudzana polem elektrycznym fali świetlnej (≈ jednorodnym).
1
2. Klastry i nanocząstki
Klastry (małe klastry) wykazują właściwości wyraźnie zależne od właściwości
atomów; liczba atomów: od kilku do ≈100 (Au, Ag: 59 atomów w 1 nm3).
Nanocząstki (duże klastry) mają właściwości dużego objętościowo metalu.
Widmo optyczne atomowego sodu
(589.3, 589.6 nm),
widmo jonizacji Na3 ,
widmo absorpcji Na8 ,
widmo absorpcji dużych klastrów
(nanocząstek) Na w NaCl,
transmisja litej warstwy metalicznej
Na o grubości 10 nm.
2
3. Małe klastry.
Schemat aparatury do badań optycznych własności klastrów. Metaliczne srebro jest
rozpylane wiazką jonów Xe+ (23 keV), atomy i klastry Ag o różnych ładunkach
elektrycznych są wyciągane soczewką elektrostatyczną L1 , rozdzielane w
kwadrupolowym spektrometrze masowym QMS i osadzane na płytce CaF2 w 10 K
(typowy prąd jonowy: 2-4 nA). Na rysunku pominięto wiązkę atomów Ar, która
wymrażając się na płytce CaF2 stanowi matrycę, w której osadzają się klastry Ag.
Spex – monochromatory, PM – fotopowielacze, D2 – lampa deuterowa (źródło
UV), W – lampa wolframowa (żarówka halogenowa) stanowią układ do pomiaru
absorpcji światła i fluorescencji próbki klastrów.
S. Fedrigo, W. Harbich, J. Buttet –(1993)
3
Widma absorpcji klastrów Ag o różnej wielkości w matrycy Ar. Punkty i kreski – wyniki obliczeń i średnie położenia pasm
absorpcji. Nieregularności w położeniu pasm absorpcji klastrów wynikają z tworzenia zamkniętych powłok przy pewnych
liczbach atomów (są to tzw. liczby magiczne).
4
Wielkość nanocząstek ma wpływ na ich właściwości fizyczne. Poniżej: szerokość
linii w rentgenogramach (metoda θ-2θ) zależy od rozmiarów cząstek. Średnice i
masy cząsteczkowe klastrów podane w tysiącach j.m.at. (masa atomowa Au: 197).
Upakowanie atomów Ag i Au: ≈ 59 atomów w 1 nm3.
915 atomów
330 atomów
152 atomy
110 atomów
71 atomów
41 atomów
AccChemRes 32
5
Wzór Bragga 2d sin θ = nλ
określa kierunek promienia odbitego
względem promienia padającego (2θ),
gdy ugięcie i interferencja fali
promieniowania X zachodzi na
nieskończonych płaszczyznach.
Gdy płaszczyzny kryształu mają
rozmiary tylko ≈10-100 razy większe od stałej sieci (d), to kątowa szerokość
prążka stanowi miarę wielkości płaszczyzn krystalicznych (wielkości kryształu).
Średni rozmiar - z kątowej szerokości linii w rentgenogramach - z wzoru
Debye-Scherrera:
D=
Kλ
∆ ⋅ cos θ
K – czynnik zależny od kształtu (≈0.9); λ - długość fali (Cu Kα: 1.54 Å)
θ - kąt ugięcia, ∆ - szerokość kątowa prążka (FWHM).
Przykład: rentgenogram nanokryształów TiO2
10000
8000
2E+4
100 nm
XRD 13.01.2015
Cu Kα λ = 1.54 A
0.8 - 11 nm
6000
4000
2000
0
1E+4
36
38
40
42
44
46
48
50
0E+0
20
30
40
50
60
2θ (deg)
6
70
80
90
4. Duże klastry (nanocząstki) metaliczne
Gdy średnica nanocząstki przekracza 2.5-3 nm (dla Ag i Au: 59 atomów/nm3), to
jej właściwości stają się powiązane z właściwościami dużych objętości (bulk)
metalu. Wśród własności optycznych i spektralnych takich nanocząstek najbardziej
charakterystyczne jest występowanie rezonansu plazmonowego. Przejawia się on
w postaci wzmożonej absorpcji i wzmożonego rozpraszania światła w pasmach
spektralnych o szerokości kilkudziesięciu nm, z reguły w UV-Vis.
Plazmon
Powstaje w objętości i przy powierzchni przewodnika, wzbudzany polem
elektrycznym fali świetlnej o częstości zbliżonej do częstości drgań własnych gazu
elektronowego.
+σ
σ
+ + + + + + + + + + + + +
x – przesunięcie gazu elektronowego
względem nieruchomych rdzeni atomów
E
_ _ _ _ _ _ _ _ _ _ _ _ _
-σ
σ
Przesunięcie elektronów znajdujących się w pewnej objętości powoduje
wystąpienie pola elektrycznego pochodzącego od nadmiarowych ładunków na
powierzchniach, zawracającego przesunięte ładunki do położenia równowagi.
E=
σ [e(xnS )] / S ne
=
=
x
ε0
ε0
ε0
Elektrony wykonują więc ruch harmoniczny:
d 2x
ne2
m 2 = −eE = −
x
dt
ε0
→
7
ne 2
ω =
ε 0m
2
p
Pole elektryczne o częstości ωp (i częstościach zbliżonych) powoduje wystąpienie
rezonansowych oscylacji gęstości elektronowej. Rzecz ma się jednak tak prosto
jedynie w plazmie (zjonizowanym gazie). W metalach, a szczególnie silnie w
półprzewodnikach, elektrony nie są całkiem swobodne a w ich ruchu przejawiają
się ich właściwości takie jak masa efektywna, ruchliwość, średnia droga swobodna
itp., a także ograniczenia przestrzenne (kwantowanie rozmiarowe).
Ponadto częstość plazmonowa zależy od kształtu i rozmiarów bryłki metalu.
Zadanie:
Obliczyć częstość plazmonową srebra wg modelu elektronów swobodnych.
e = 1.6⋅10-19 C, ε0 = 8.85⋅10-12 C2/Nm2 , m = 0.91⋅10-30 kg , 59 atomów/nm3.
Uwaga: wynik jest zawyżony ok. dwukrotnie jeżeli założymy, że koncentracja
elektronów swobodnych jest równa koncentracji atomów.
Absorpcja światła przez nanocząstki metaliczne
Swiatło przechodzące przez zawiesinę zawierającą w jednostce objętości N cząstek
metalicznych ulega osłabieniu wskutek absorpcji jego energii we wnętrzu cząstek.
Jeżeli intensywność padającej wiązki światła wynosi I0 , to na drodze d zmniejsza
się do wartości I, przy czym:
I 
A = log10  0  = N ⋅ C ⋅ d 2.303
 I 
C=
2π
k2
∑ (2n + 1) Re(a
n
+ bn )
n
k = 2π ε m λ
gdzie εm jest przenikalnością dielektryczną ośrodka otaczającego cząstki (np.
cieczy), zaś an oraz bn są funkcjami Ricattiego-Bessela dla argumentu zależnego od
promienia cząstek R oraz od długości fali światła λ. Zamiast wielkości C
wygodniej jest używać molowego współczynnika ekstynkcji odniesionego do
molowego stężenia metalu występującego w postaci cząstek koloidalnych:
8
3 ⋅ 10 −3 Vm C
σ [M cm ] =
4π ⋅ 2.303 ⋅ R 3
−1
−1
(M oznacza mol/litr)
gdzie Vm [cm3/mol] jest objętością molową metalu. Według elektrodynamiki
klasycznej (Mie 1908) dla cząstek małych, dla których kR << 1, dobrym
przybliżeniem dla wielkości C jest wzór:
C=
24π 2 R3ε m3/ 2
λ
⋅
ε ''
(ε '+ 2ε m )
2
+ ( ε '')
2
ε = ε’ + i ε’’ jest zespoloną przenikalnością dielektryczną cząstek – ich funkcją
dielektryczną.
Barwa koloidów metalicznych wynika ze wzmożonej absorpcji światła, która
występuje gdy ε’= − 2εm .
Gdy cząstki są pokryte warstwą dielektryczną o przenikalności εs to:
 (ε − ε m )(ε − 2ε s ) + (1 − g )(ε − ε s )(ε m + 2ε s ) 
C = 4πR 2 k ⋅ Im s

(
)(
)
(
)(
)(
)
ε
2
ε
ε
2
ε
1
g
2
ε
2
ε
ε
ε
+
+
+
−
−
−
m
s
s
m
s 
 s
g - ułamek objętości cząstek przypadającej na powłokę, R - promień cząstki wraz z
powłoką, εm i εs są przenikalnościami ośrodka i powłoki.
W metalach (Au, Ag, Pt, Al,...) absorpcja w zakresie spektralnym sięgającym
częstości plazmowej wynika z własności swobodnych elektronów, a funkcja
dielektryczna dla częstotliwości optycznych jest dobrze opisywana przez teorię
Drudego. Według tej teorii:
2
ω
ε '= ε ∞ − 2 p 2
ω + ωd
ε''=
ω 2pω d
ω (ω 2 + ω d2 )
gdzie ε ∞ jest graniczną przenikalnością dielektryczną dla wysokich częstości
(powiązaną z przejściami międzypasmowymi i w powłokach wewnętrznych
atomów) a ωp jest częstością plazmową (por. powyżej):
9
2
ω p = ne mε
0
a wielkość ωd ma związek z tłumieniem ruchu elektronów („tarciem”) i zależy od
średniej drogi swobodnej Rb i od prędkości elektronów o energii Fermiego (vF):
ωd =
vF
Rb
Powyżej zdefiniowane wielkości odpowiadają ruchowi elektronów w
nieograniczonej bryle metalu. Gdy jednak promień cząstki metalicznej R staje się
mniejszy od średniej drogi swobodnej, to elektrony są dodatkowo rozpraszane na
ograniczającej ich ruch powierzchni, średnia droga swobodna ulega skróceniu i w
powyższym wzorze w miejsce Rb należy podstawić mniejszą efektywną wartość
średniej drogi swobodnej Ref z wzoru:
1
1
1
= +
Ref R Rb
W ten sposób efektywna wartość drogi swobodnej wpływa na wartość ωp i
pośrednio na funkcję dielektryczną ε’ i ε”, oraz na pasmo absorpcji nanocząstek w
stopniu zależnym od ich rozmiaru.
10