Kier

1. Ruch elektronów w polu elektrycznym w środowisku materialnym; założenia, opis ruchu (równania,
zależności), ruchliwość, rezystywność fononowa i resztkowa.
Założenia:
• czas ruchu swobodnego (bezkolizyjnego) jest równy τ
• zderzenia redukują prędkość elektronu do wartości v=0
Równania:
Ruchliwość zależy od czasu τ , zależy więc od swobodnej drogi elektronu i jego prędkości w jednostkowym
polu elektrycznym.
Ruchliwość jest miarę prędkości elektronu w polu elektrycznym o jednostkowym natężeniu.
Odwrotnością konduktywności jest rezystywność ρV.
rezystywność jest wyrażana w omometrach (Ωm).
Rezystywno Rezystywność fononowa i fononowa i resztkowa:
Ze względu na wyróżnianie rozpraszania energiina fononach (drgającej siatce krystalicznej) na defektach,
wydziela się w definicji rezystywność:
• tzw. rezystywność fononową (opór fononowy), zależna od temperatury i
• rezystywność resztkową (opór resztkowy) związany z defektami sieci i od temperatury zwykle niezależny.
• Oba składniki występują we wzorze znanym pod nazwą reguły Matthiessena
Składnik fononowy może być w szerokim zakresie temperatur wysokich temperatur opisany liniową
zależnością.
• W niskich temperaturach zależność ta za pośrednictwem prawa Blocha zmienia się proporcjonalnie do T5
• Można zatem przyjąć, że w temperaturach T>300K obowiązuje zależność
natomiast w temperaturach niskich, poniżej temperatury Debye (T<< ΘD) jest
• W ramach teorii pasmowej można wyprowadzić następującą zależność na rezystywność resztkową
m - masa elektronu, vF - prędkość elektronu na poziomie Fermiego, le – droga swobodna elektronu.
W ramach teorii pasmowej rezystancja resztkowa (pozostałościowa) jest opisana wzorem
Gdzie: e - ładunek elektronu, m – masa elektronu, le – średnia droga swobodna elektronu.
Z wzoru wynika, że im mniejsza jest średnia droga swobodna le, tym , tym większa jest rezystywność.
Wprowadzenie domieszek zmniejsza le, a więc zwiększa rezystywność.
2. Dowód stałości indukcji we wnętrzu idealnego przewodnika (zasada niezmienności strumienia
magnetycznego w nadprzewodniku). Opisać różnice między zachowaniem idealnego przewodnika i
nadprzewodnika w zewnętrznym polu magnetycznym. Co to jest idealny diamagnetyzm.
Idealny przewodnik:
lub
Dla
jest
oraz
Z równania
wynika
oraz
Indukcja magnetyczna we wnętrzu idealnego przewodnika (IP) jest stała w czasie.
Rozważamy dwa przypadki:
• przewodnik (IP) chłodzony w zewnętrznym polu magnetycznym
• pole zostało przyłożone po ochłodzeniu (IP) poniżej Tc
Oziębienie (IP) i usunięcie pola.
Oziębienie (IP) i usunięcie pola.
Etap A
B>0
T>Tc
Etap B
B>0
T<Tc
Pole magnetyczne nie ulega
zmianie -pole skojarzone z
przewodnikiem pozostaje bez
zmiany
Oziębienie (IP) i usunięcie pola.
Po usunięciu pola magnetycznego zewnętrznego,
pole skojarzone z przewodnikiem nie ulega zmianie
Etap C
B=0
T<Tc
Oziębienie (IP) i usunięcie pola.
Pole magnetyczne przyłożone po oziębieniu (IP) do T<Tc
Tak było
Tak było
Tak jest
Po usunięciu pola magnetycznego,
pole skojarzone z przewodnikiem
pozostaje.
Tak jest
Pole magnetyczne nie wnika do wnętrza idealnego przewodnika.
Pole magnetyczne w nadprzewodniku (S)
Etap A: pole B>0 przy T>Tc,
Etap B: obniżenie temperatury do T<Tc,
B>0, T>Tc
B>0, T<Tc
a) Jeżeli umieszczamy nadprzewodnik w polu magnetycznym przy T>Tc , to pole wnika do jego wnętrza.
Po obniżeniu temperatury do T<Tc pole zostaje wyparte z nadprzewodnika.
b) W temperaturze T<Tc pole magnetyczne nie wnika do nadprzewodnika.
Jest to zjawisko Meissnera –Ochsenfelda
Zjawisko to nie jest prostą konsekwencją zerowego oporu elektrycznego, lecz drugą podstawową
właściwością stanu nadprzewodzącego.
Zjawisko to obserwujemy w dwóch przypadkach:
1. Po oziębieniu nadprzewodnika (do T< Tc), polu magnetycznym, strumień magnetyczny jest z
nadprzewodnika wypierany,
2. Do nadprzewodnika oziębionego (T<Tc) strumień nie wnika.
Rezultatem zjawiska Meissnera jest tzw. lewitacja tj. unoszenie nadprzewodnika w polu magnetycznym.
Lewitacja polega na „zawieszeniu” nadprzewodnika w polu magnetycznym.
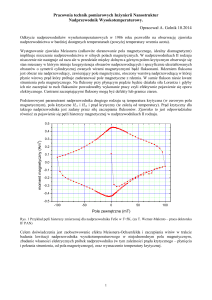
3. Zasada pomiaru rezystancji (rezystywności) nadprzewodnika przy T<Tc (opis metody, wzory, wykres
zanikania prądu, dane doświadczalne dotyczące czasu zanikania prądu i wartości rezystywności).
Ponieważ bezpośredni pomiar rezystancji nie jest możliwy, mierzy się ją metod metodą po pośrednią.
Polega ona na pomiarze czasu zanikania prądu w nadprzewodzącym pierścieniu.
Z równania napisanego dla pierścienia o rezystancji R
i indukcyjności L;
Otrzymujemy;
Gdzie: stała czasowa;
A. Badania Kamerlinha Onnesa : Występują bardzo małe, niemierzalne, wartości R.
B. Quinn i Ittner: w nadprzewodzącym walcu Pb (L=1,4 10-13 H).
Wynik:
Jest to ok. 1017 razy mniej (!!) niż ρCu w temp. pokojowej.
C. File, Mills – Nb075Zr025
(Metodą jądrowego rezonansu magnetycznego):
Wynik czas połowicznego zaniku nie mniejszy niż 100 000 lat !!!
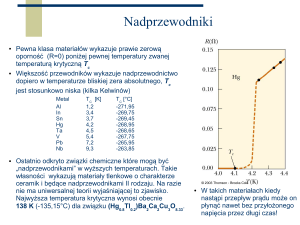
4. Charakterystyczne cechy nadprzewodników I i II rodzaju (Co to jest nadprzewodnictwo,
charakterystyki fazowe nadprzewodnika I i II rodzaju, interpretacja).
W roku 1908 został skroplony ciekły hel (T~4K). Autorem tego osiągnięcia był holenderski fizyk Heike
Kamerlingh Onnes.
W rezultacie tego wynalazku w roku 1911 prowadzono badania Pt i Hg w temperaturach rzędu 4K.
Wyniki:
Platyna(Pt) – rezystywność maleje do b. małej wartości.
Rtęć(Hg) – zaobserwowano anomalny przebieg R(T).
Ze względu na „czystość” rtęci oczekiwano:
Nowy stan materii: STAN NADPRZEWODZĄCY
Temperatura przejścia – temperatura krytyczna:
Przykłady nadprzewodników:
Charakterystyka fazowa nadprzewodnika I rodzaju:
Przy natężeniu pola magnetycznego o wartości większej od pewnej wartości krytycznej (w danej
temperaturze) H > Hc następuje utrata stanu nadprzewodzącego.
Pole Hc jest termodynamicznym polem krytycznym. Pole Hc zależy od temperatury T, w której znajduje się
nadprzewodnik.
„Drogi” przejścia do stanu normalnego:
Nadprzewodniki II rodzaju:
Istotną cechą nadprzewodników II rodzaju jest specyficzna konfiguracja pola w nadprzewodniku. Wynika
ona z energetycznego bilansu na granicy przejścia pomiędzy fazą nadprzewodzącą (S) i fazą normalną.
Ważne są tu następujące parametry:
Lordowska głębokość wnikania:
Rozkład koncentracji elektronów nadprzewodzących:
Odległość koherencji:
Długość drogi swobodnej:
Teoria Ginzburga-Landaua nadprzewodniki II rodzaju:
Przewidywanie, że występuje:


Wnikanie pola magnetycznego do nadprzewodnika,
Trzecia faza w charakterystyce fazowej, tzw. faza mieszana (faza Szubnikowa),
W odróżnieniu od modelu Londonów, w którym przyjęto ns=const. teoria G-L, przyjmuje rozkład
koncentracji elektronów ns(x,T).
W rezultacie otrzymujemy 2 konkurencyjne energie:

Energia pola magnetycznego:

Energię rozkładu nadprzewodzących elektronów:
Minimalizacja ich różnicy decyduje o utworzeniu bariery energetycznej na granicy:
nadprzewodnik (S) – obszar normalny (N)
Równania Ginzburga- Landara:
Wyróżnia się tu dwa „rodzaje” energii:
Energia pola magnetycznego wnikającego do nadprzewodnika,
Energia związana z rozkładem nadprzewodzących elektronów.
Energia pola magnetycznego
Energię rozkładu nadprzewodzących elektronów
Bariera energetyczna:
Wartość parametru Gizburga-Landauajest podstawą podziału nadprzewodników na nadprzewodniki I i II
rodzaju:

Jeżeli spełniony jest warunek
to nadprzewodnictwo istnieje w polu H<Hc i towarzyszy mu całkowite wypchnięcie pola magnetycznego z
nadprzewodnika

Jeżeli spełniony jest warunek
to nadprzewodnictwo istnieje w polu H<Hc2 i nie występuje tu całkowite wypchnięcie pola magnetycznego z
nadprzewodnika
Oba parametry zależą od temperatury T i od drogi swobodnej elektronów ls
Zmniejszenie drogi swobodnej powoduje:
a) mały wzrost Londonowskiej głębokości wnikania
b) znaczne zmniejszenie odległości koherencji
Zmniejszenie drogi swobodnej powoduje: wzrost parametru Ginzburga-Landaua, przejście w kierunku
nadprzewodnictwa II rodzaju
Londonowska głębokość wnikania
Odległość koherencji
Konsekwencją ujemnej bariery energetycznej jest dążenie do tworzenia jak największej powierzchni
granicznej stref nadprzewodzących i normalnych. Prowadzi to do tworzenie cylindrycznych „tworów”
elektromagnetycznych tj. podziału pola magnetycznego na fluksony objęte wirami prądowymi tj. do
tzw. wirów Abrikosowa.
Wir Abrikosowa:
Kwant strumienia magnetycznego.
Obszar wiru jest traktowany jak obszar normalny – nie nadprzewodzący.
Charakterystyka fazowa nadprzewodnika II rodzaju:
W nadprzewodniku II rodzaju wyróżniamy dwie krytyczne wartości natężenia pola:
Pole krytyczne Hc1, Pole krytyczne Hc2

Przy H<Hc1pole nie wnika do nadprzewodnika. Jest to tzw. stan Meissnera.

Przy H>Hc2 następuje utrata nadprzewodnictwa.
Przy
Hc1<H<Hc2 występuje tzw. Stan mieszany (B>0) inaczej: Faza Szubnikowa.
Charakterystyka fazowa:
1. Dla 0<H<Hc1(T) przy T<Tc stan Meissnera. Pole magnetyczne jest całkowicie wypierane z
nadprzewodnika.
2. Dla Hc1<H<Hc2(T) przy T<Tc stan mieszany. Pole magnetyczne wypełnia nadprzewodnik w postaci
wirów.
3. Dla H>Hc2(T) przy T<Tc stan normalny. Pole magnetyczne wypełnia nadprzewodnik w postaci strumienia
ciągłego (wiry znikają).
Przykłady nadprzewodników II rodzaju:
Dla uzyskania B=0, nadprzewodnik tworzy w tzw. stanie mieszanym cylindryczne obszary stanu normalnego
zwane wirami. Pole pozostaje również w powierzchniowej warstwie o grubości = Londonowskiej głębokości
wnikania.
5. Prąd powierzchniowy w nadprzewodnikach I rodzaju (Model Londonów, wyprowadzenie równań,
wykresy rozkładu pola magnetycznego w nadprzewodniku, interpretacja).
Założenie: R=0
Z I równania dynamiki:
gdzie:
v – prędkość elektronu, m – masa elektronu, F - siła działająca na elektron (pochodząca od pola
elektrycznego)
Oznaczamy:
q – ładunek elektronu, j – gęstość prądu (wynikająca z ruchu elektronów)
Po podstawieniu:
mamy:
Jeżeli zapiszemy:
to
Jest to wzór określający zmianę w czasie gęstości prądu w wyniku działania pola elektrycznego (E) na
elektrony w ośrodku bez rezystancyjnym (R=0).
Pod wpływem stałego pola E=const., elektrony poruszaj się ruchem jednostajnie przyspieszonym, co
powoduje liniowe (proporcjonalne do pola E) narastanie prądu j (dj/dt=cont.).
Wprowadzamy:
Wynika stąd:
Po zróżniczkowaniu:
Z prawa Maxwella
Jest to różniczkowa forma zapisu prawa, które w postaci całkowej ma formę:
Gdzie strumień magnetyczny:
Z poprzednio wyprowadzonego wzoru:
Wynika:
Lewa strona równania:
może być przekształcona w następujący sposób:
Ponieważ grad(div x)=0 – pole bez źródłowe, to:
Stąd
Wprowadzamy wielkość:
oraz
nazywaną Londonowską głębokością wnikania (wymiar metr)
Stąd
Równanie ma postać:
gdzie oznaczono
Równanie dotyczy pochodnej w czasie indukcji B tj. zmiennego w czasie pola magnetycznego. Po
scałkowaniu względem czasu otrzymujemy wniosek B=const.
Równanie to wykazuje, więc, że konsekwencją prawa Ohma i zerowego oporu (nieskończonego
przewodnictwa) jest tylko stała w czasie, wartość pola magnetycznego.
Założenie zerowej wartości oporu elektrycznego ośrodka, prowadzi do wniosku, że w ośrodku takim nie może
istnieć (poza powierzchnią) zmienne pole magnetyczne. Pochodna pola dB/dt, zanika w warstwie
powierzchniowej wg funkcji, eksponencjalnej.
Rozwiązanie równania
względem czasu daje w wyniku stałą w czasie wartość indukcji.
Rozkład przestrzenny pola magnetycznego w ogólnym przypadku jest opisany
wzorem:
Zerowy opór daje, więc w konsekwencji rozkład pola magnetycznego wewnątrz idealnego przewodnika w
postaci przebiegu malejącego ku osi.
Z doświadczenia wynika jednak, że pole to jest nie tylko stałe, ale równe zeru. Londonowie intuicyjnie
przyjęli rozwiązanie szczególne równania, a mianowicie rozwiązanie:
Oznacza to, że równanie uprzednio zapisane w odniesieniu do pochodnej w czasie indukcji B, dotyczy
również indukcji:
Rozwiązanie dla płaskiej granicy nadprzewodnik-próżnia.
Dla przypadku jednowymiarowego równanie Londonów ma postać:
Jest to równanie względem współrzędnej x..
Przyjmujemy, że dla x>0 mamy obszar jednorodnego, nieskończonego nadprzewodnika. Pole magnetyczne
jest równoległe do powierzchni.
Rozwiązanie równania:
Zastępcza głębokość wnikania.
Wynik ten oznacza, że LGW jest zastępczą głębokością na której, strumień magnetyczny przy stałej indukcji
Ba :
ma taką samą wartość jak strumień przy rzeczywistym rozkładzie indukcji
B(x)=Ba exp(-x/ λL).
6. Na czym polega intuicyjne założenie Londonów. Co to jest Londonowska głębokość wnikania-wzór,
interpretacja, Zastępcza głębokość wnikania, Dlaczego we wnętrzu nadprzewodnika nie ma pola
magnetycznego (uzasadnienie fizyczne).
Z doświadczenia wynika jednak, że pole to jest nie tylko stałe, ale równe zeru. Londonowie intuicyjnie
przyjęli rozwiązanie szczególne równania, a mianowicie rozwiązanie:
Oznacza to, że równanie uprzednio zapisane w odniesieniu do pochodnej w czasie indukcji
B, dotyczy również indukcji:
Rozwiązanie dla płaskiej granicy nadprzewodnik-próżnia.
Dla przypadku jednowymiarowego równanie Londonów ma postać:
Jest to równanie względem współrzędnej x..
Przyjmujemy, że dla x>0 mamy obszar jednorodnego, nieskończonego nadprzewodnika. Pole magnetyczne
jest równoległe do powierzchni.
Rozwiązanie równania:
Zastępcza głębokość wnikania.
Wynik ten oznacza, że LGW jest zastępczą głębokością na której, strumień magnetyczny przy stałej indukcji
Ba :
ma taką samą wartość jak strumień przy rzeczywistym rozkładzie indukcji
B(x)=Ba exp(-x/ λL).
Aby pole magnetyczne wewnątrz nadprzewodnika zanikało, praktycznie do zera, w warstwie
przypowierzchniowej nadprzewodnika o głębokości λL musi płynąc prąd nadprzewodzący. Jest to prąd
ekranujący. Prąd ekranujący wytwarza we wnętrzu nadprzewodnika pole magnetyczne, przeciwne do pola
zewnętrznego, znosząc je całkowicie.
Prąd płynie przez warstwę przypowierzchniową o głębokości λL:
7. Powierzchniowe prądy ekranujące ? Co to jest prąd krytyczny ? W jaki sposób prąd krytyczny
związany jest z polem magnetycznym ? Rozkład pola magnetycznego w nadprzewodzącym walcu.
Aby pole magnetyczne wewnątrz nadprzewodnika zanikało, praktycznie do zera, w warstwie
przypowierzchniowej nadprzewodnika o głębokości λL musi płynąc prąd nadprzewodzący. Jest to prąd
ekranujący. Prąd ekranujący wytwarza we wnętrzu nadprzewodnika pole magnetyczne, przeciwne do pola
zewnętrznego, znosząc je całkowicie.
Prąd płynie przez warstwę przypowierzchniową o głębokości λL:
Prąd krytyczny – krytyczna gęstość prądu
Ponieważ przy H=Hc następuje wyjście ze stanu nadprzewodnictwa i przejście do stanu normalnego, to
istnieje pewien prąd krytyczny odpowiadający temu stanowi: I =Ic
Dla nadprzewodnika w postaci walca mamy:
oraz przy
jest
Wynika stąd:
a) Dla wnętrza walca ( w założeniu, że gęstość prądu jest jednakowa w całym przekroju poprzecznym), na
głębokości x
Zależność ma charakter liniowy.
Na zewnątrz walca:
Jeżeli
Wynika stąd, że:
H=Hc, to I=Ic.
oraz
Krytyczna gęstość prądu:
Gęstość prądu w nadprzewodniku
Obliczeniowa gęstość prądu:
W stanie krytycznym:
Rzeczywista gęstość prądu
W stanie krytycznym:
Oszacowanie:
Jeżeli przyjmiemy
To
Jeżeli Bc =
1T
8. Zastępcza głębokość wnikania (wykazać, że Londonowska głębokość wnikania jest głębokością
zastępczą-wyprowadzenie wzoru, interpretacja).
Zastępcza głębokość wnikania.
Wynik ten oznacza, że LGW jest zastępczą głębokością na której, strumień magnetyczny przy stałej indukcji
Ba :
ma taką samą wartość jak strumień przy rzeczywistym rozkładzie indukcji
B(x)=Ba exp(-x/ λL).
9. Kwanty strumienia magnetycznego: wykaż, że strumień magnetyczny w nadprzewodniku może
istnieć tylko w postaci kwantów (fluksonów) (założenia teorii, ilustracja rysunkowa, fala elektronowa,
pęd w polu magnetycznym, wyprowadzenie wzorów: fluksoid, flukson, interpretacja wzorów
interpretacja wyniku).
Z mechaniki kwantowej wynika, że stany stacjonarne układów fizycznych są określone przez warunki
kwantowe.
Tezę taką przedstawił London zakładając, że: Strumień magnetyczny przechodzący przez nadprzewodzącą
pętlę nie może przyjmować dowolnych wartości.
Teza:
Wartość strumienia może być tylko wielokrotnością pojedynczej porcji - kwantu
strumienia.
Nośnikami ładunku w nadprzewodnikach są tzw. „pary Coopera”.
Układ dwóch związanych ze sobą – przyciągających się – elektronów.
Odległość elektronów pary - długość koherecji: ξ
Elektrony pary Coopera mają przeciwnie skierowane pędy i spiny. Wypadkowy pęd pary jest równy zeru.
Długość koherencji - przykłady:
Funkcja falowa elektronu
Mechanika kwantowa opisuje cząstkę za pomocą fali
Wykres fali
Dla t=t1 oraz t=t2 ruch fali elektronowej:
Gradient fazy (zmiana fazy) fali elektronowej na drodze od A do B:
Długość fali elektronowej
Pęd pary elektronowej w polu magnetycznym jest równy
Człon wynikający z ruchu elektronu w polu magnetycznym:
Stąd
Z wzoru:
otrzymuje się:
Dalsze przekształcenie:
Wyrażenie na prędkość elektronu:
Zmiana fazy fali pary elektronowej na drodze od A do B - wzór przekształcony
Całkowanie po drodze zamkniętej. Zmianę fazy na drodze zamkniętej:
Całkowita zmiana fazy na drodze zamkniętej (powrót do tego samego punktu)
k – liczba całkowita
Warunek istnienia na obwodzie całkowitej liczby fal
To
Dla drogi całkowania położonej dostatecznie daleko od krawędzi otworu
oraz
Z teorii pola magnetycznego
Całka powierzchniowa z indukcji jest równa strumieniowi magnetycznemu przenikającemu przez
powierzchnię s.
Dla k=1 (jeden obieg linii całkowania)
Jest to najmniejsza porcja strumienia magnetycznego tzw. Kwant strumienia (flukson)
Kwanty strumienia magnetycznego (fluksony) występują zawsze, gdy pole magnetyczne przenika przez
nadprzewodnik. Zjawisko kwantowania strumienia odgrywa zasadniczą rolę w tzw. nadprzewodnikach II
rodzaju, do których strumień magnetyczny wnika w postaci kwantów lub „pęków” kwantów.
Wszystkie pary Coopera znajdują się w identycznych stanach, są skorelowane ze sobą. Wynika stąd, że
zgodne są ich fazy. W przypadku zmiany strumienia przenikającego przez pierścień o jeden kwant, faza par
Coopera zmienia się o
10. Krytyczna gęstość prądu w nadprzewodniku w postaci walca: gęstość obliczeniowa, gęstość
rzeczywista. Jak zmienia się gęstość obliczeniowa i rzeczywista, jeżeli rośnie średnica walca.
Ponieważ przy H=Hc następuje wyjście ze stanu nadprzewodnictwa i przejście do stanu normalnego, to
istnieje pewien prąd krytyczny odpowiadający temu stanowi: I =Ic
Dla nadprzewodnika w postaci walca mamy:
oraz przy
jest
Wynika stąd:
b) Dla wnętrza walca ( w założeniu, że gęstość prądu jest jednakowa w całym przekroju poprzecznym), na
głębokości x
Zależność ma charakter liniowy.
Na zewnątrz walca:
Jeżeli H=Hc, to I=Ic. Wynika stąd, że:
oraz
Krytyczna gęstość prądu:
Gęstość prądu w nadprzewodniku
Obliczeniowa gęstość prądu:
W stanie krytycznym:
Rzeczywista gęstość prądu
W stanie krytycznym:
Oszacowanie:
Jeżeli przyjmiemy
To
Jeżeli Bc = 1T
11. Pole magnetyczne cylindrycznego nadprzewodnika z prądem. Wyprowadzenie wzoru na natężenie
pola wewnątrz i na zewnątrz nadprzewodnika. Wykresy. Różnica pomiędzy rozkładem pola
nadprzewodnika i przewodnika.
Dla nadprzewodnika w postaci walca mamy:
oraz przy
jest
Wynika stąd:
c) Dla wnętrza walca ( w założeniu, że gęstość prądu jest jednakowa w całym przekroju poprzecznym), na
głębokości x
Zależność ma charakter liniowy.
Na zewnątrz walca:
Jeżeli
Wynika stąd, że:
H=Hc, to I=Ic.
oraz
12. Charakterystyki magnesowania nadprzewodnika [idealna, rzeczywista w skali B(H) i –M(H)].
Nadprzewodnik jako idealny diamagnetyk (rozważyć wartość µr). Porównanie charakterystyki
magnesowania nadprzewodnika i innych ciał stałych (ferromagnetyków, paramagnetyków i
diamagnetyków). Podać odpowiednie wzory.
Opis pola magnetycznego w nadprzewodniku
gdzie: o – przenikalność magnetyczna próżni (4 10-7 H/m), H – natężenie pola magnetycznego (A/m),
M – namagnesowanie (A/m).
Ponieważ:
to
Przy innej formie zapisu:
Wobec
jest
gdzie: o - przenikalność magnetyczna, r - względna przenikalność magnetyczna.
Zerowa wartość przenikalności
dowodzi, że nadprzewodnik w temperaturze T<Tc jest
Idealnym diamagnetykiem!
Charakterystyka magnesowania nadprzewodnika idealnego B=f(H)
Charakterystyka magnesowania nadprzewodnika rzeczywistego B=f(H)
Charakterystyka magnesowania nadprzewodnika
–M=f(H)
13. Wykazać, że strumień magnetyczny sprzężony z nadprzewodzącą cewką nie może zmienić się w
czasie (przy T<Tc) . Co jest powodem podtrzymania tego strumienia magnetycznego w przypadku
usunięcia pola zewnętrznego.
Zasada niezmienności strumienia magnetycznego
Całkowity strumień magnetyczny przechodzący przez powierzchnię otoczoną obwodem magnetycznym nie
ulega zmianie.
Oznacza to, że zmniejszenie pola zewnętrznego (Φ) towarzyszy
wzrost pola „własnego” Li, czyli wzrost prądu i.
Jest to cecha towarzysząca R=0 ( nie tylko nadprzewodnik ale także idealny przewodnik).
Wynika stąd:
14. Uzasadnienie energetyczne nadprzewodnictwa II rodzaju (rozważyć energię magnetyczną i energię
nadprzewodzących elektronów w strefie granicznej, narysować odpowiednie wykresy, omówić
kryterium nadprzewodnictwa pierwszego i drugiego rodzaju ).
Nadprzewodniki II rodzaju:
Istotną cechą nadprzewodników II rodzaju jest specyficzna konfiguracja pola w nadprzewodniku. Wynika
ona z energetycznego bilansu na granicy przejścia pomiędzy fazą nadprzewodzącą (S) i fazą normalną.
Ważne są tu następujące parametry:
Lordowska głębokość wnikania:
Rozkład koncentracji elektronów nadprzewodzących:
Odległość koherencji:
Długość drogi swobodnej:
Teoria Ginzburga-Landaua nadprzewodniki II rodzaju:
Przewidywanie, że występuje:


Wnikanie pola magnetycznego do nadprzewodnika,
Trzecia faza w charakterystyce fazowej, tzw. faza mieszana (faza Szubnikowa),
W odróżnieniu od modelu Londonów, w którym przyjęto ns=const. teoria G-L, przyjmuje rozkład
koncentracji elektronów ns(x,T).
W rezultacie otrzymujemy 2 konkurencyjne energie:

Energia pola magnetycznego:

Energię rozkładu nadprzewodzących elektronów:
Minimalizacja ich różnicy decyduje o utworzeniu bariery energetycznej na granicy:
nadprzewodnik (S) – obszar normalny (N)
Równania Ginzburga- Landara:
Wyróżnia się tu dwa „rodzaje” energii:
Energia pola magnetycznego wnikającego do nadprzewodnika,
Energia związana z rozkładem nadprzewodzących elektronów.
Energia pola magnetycznego
Energię rozkładu nadprzewodzących elektronów
Bariera energetyczna:
Wartość parametru Gizburga-Landauajest podstawą podziału nadprzewodników na nadprzewodniki I i II
rodzaju:

Jeżeli spełniony jest warunek
to nadprzewodnictwo istnieje w polu H<Hc i towarzyszy mu całkowite wypchnięcie pola magnetycznego z
nadprzewodnika

Jeżeli spełniony jest warunek
to nadprzewodnictwo istnieje w polu H<Hc2 i nie występuje tu całkowite wypchnięcie pola magnetycznego z
nadprzewodnik
Oba parametry zależą od temperatury T i od drogi swobodnej elektronów ls
Zmniejszenie drogi swobodnej powoduje:
a) mały wzrost Londonowskiej głębokości wnikania
b) znaczne zmniejszenie odległości koherencji
Zmniejszenie drogi swobodnej powoduje: wzrost parametru Ginzburga-Landaua, przejście w kierunku
nadprzewodnictwa II rodzaju
Londonowska głębokość wnikania
Odległość koherencji
Konsekwencją ujemnej bariery energetycznej jest dążenie do tworzenia jak największej powierzchni
granicznej stref nadprzewodzących i normalnych. Prowadzi to do tworzenie cylindrycznych „tworów”
elektromagnetycznych tj. podziału pola magnetycznego na fluksony objęte wirami prądowymi tj. do
tzw. wirów Abrikosowa.
Wir Abrikosowa:
Kwant strumienia magnetycznego.
Obszar wiru jest traktowany jak obszar normalny – nie nadprzewodzący.
Charakterystyka fazowa nadprzewodnika II rodzaju:
W nadprzewodniku II rodzaju wyróżniamy dwie krytyczne wartości natężenia pola:
Pole krytyczne Hc1, Pole krytyczne Hc2

Przy H<Hc1pole nie wnika do nadprzewodnika. Jest to tzw. stan Meissnera.

Przy H>Hc2 następuje utrata nadprzewodnictwa.
Przy
Hc1<H<Hc2 występuje tzw. Stan mieszany (B>0) inaczej: Faza Szubnikowa.
Charakterystyka fazowa:
1. Dla 0<H<Hc1(T) przy T<Tc stan Meissnera. Pole magnetyczne jest całkowicie wypierane z
nadprzewodnika.
2. Dla Hc1<H<Hc2(T) przy T<Tc stan mieszany. Pole magnetyczne wypełnia nadprzewodnik w postaci
wirów.
3. Dla H>Hc2(T) przy T<Tc stan normalny. Pole magnetyczne wypełnia nadprzewodnik w postaci strumienia
ciągłego (wiry znikają).
Przykłady nadprzewodników II rodzaju:
Dla uzyskania B=0, nadprzewodnik tworzy w tzw. stanie mieszanym cylindryczne obszary stanu normalnego
zwane wirami. Pole pozostaje również w powierzchniowej warstwie o grubości = Londonowskiej głębokości
wnikania.
15. Proszę o podanie krótkich odpowiedzi na pytania (należy podać krótki opis + ilustracja graficzna +
ewentualne wzory):
• Co to jest spinning.
• Dlaczego siła Lorentza jest powodem „wychodzenia” ze stanu nadprzewodnictwa.
• Co to jest Hc2.
• Podaj typowe temperatury stanu nadprzewodzącego dla nadprzewodników I i II rodzaju. Charakterystyki
fazowe nadprzewodników.
• Co to jest: Londonowska głębokość wnikania, pary Coopera, flukson, stan mieszany.
• Od czego zależą wysokości poszczególnych barier energetycznych i bariery wypadkowej.
• Co to jest współczynnik Ginzburga-Landaua i dlaczego jest on podstawa klasyfikacji nadprzewodników.
• Opisać strukturę wiru Abrikosowa.
• Co jest przyczyną ruchu strumienia magnetycznego w nadprzewodniku II rodzaju.
• Pinning, siła elektromotoryczna ruchu, rezystywność i rezystancja indukowana.
• Uzasadnić, że pojawienie się rezystancji przy ruchu strumienia magnetycznego nie jest równoznaczne z
utratą nadprzewodnictwa.