Zespół Szkół Elektrycznych
w Wejherowie
Imię i Nazwisko:
Pracownia Elektryczna i Elektroniczna
Temat:
Pomiar pojemności kondensatorów
metodą techniczną
Rok szkolny
Klasa
Grupa
Data
wykonania
ćwiczenia
Data oddania
sprawozdania
Ocena
Podpis
Nr
ćwiczenia
Nr w
dzienniku
Wiadomości teoretyczne
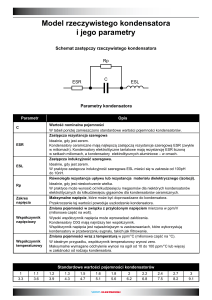
C
Kondensatory. Niektóre kondensatory wygladzaja ksztalt przebiegu pradu. Inne
przepuszczają sygnały i sprzęgają je ze sobą. Specjalne kondensatory o zmiennej
pojemności służą do przestrajania radia i wyszukiwania stacji.
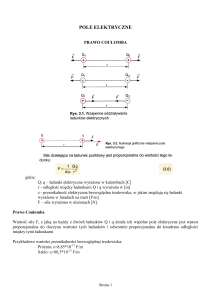
Pojemnością elektryczna nazywamy zdolność przewodników do gromadzenia
ładunków elektrycznych. Własność te wykorzystano w kondensatorach.
Kondensator to układ dwóch przewodników (elektrody, opłatki, okładziny)
przedzielonych dielektrykiem (materiałem izolacyjnym).
Jeżeli do kondensatora doprowadzimy napięcie zasilające (U) to na jego okładkach
gromadzi się ładunek równy, co do wartości, lecz przeciwnego znaku. Proces
gromadzenia ładunku nazywamy ładowaniem kondensatora. Trwa on do chwili,
gdy napięcie miedzy okładkami osiągnie wartość napięcia zasilającego. Ładunek
jednej elektrody nazywamy ładunkiem kondensatora, a zdolność kondensatora do
gromadzenia ładunku nazywamy pojemnością kondensatora C, która wyrażamy
jako stosunek ładunku zgromadzonego w kondensatorze do napięcia, przy którym
został zgromadzony. Czyli C=Q/U. Jednostka jest jeden farad (1F)
C - jest to podstawowy parametr (podstawowa wielkość) kondensatora, podawana
przez producenta. Pojemność nie zależy od ładunku i napięcia. Stosunek Q do U
jest stały dla danego kondensatora. Pojemność zależy od konstrukcji kondensatora:
a) rodzaju dielektryka (E)
b) wymiarów kondensatora.
Wytrzymałością elektryczna dielektryka nazywamy maksymalna wartość natężenia
pola, która jeszcze nie niszczy własności izolacyjnych dielektryka.
Kondensatory w układach mogą być łączone:
a) szeregowo,·b) równolegle
c) mieszanie
Cechy charakterystyczne łączenia szeregowego:, (jeżeli nie wiesz jak wygląda
łączenie szeregowe zajrzyj na stronę o rezystorach)
a) ładunki na każdym kondensatorze maja jednakowa wartość
b) napięcie całkowite przyłożone do gałęzi jest suma napiec na poszczególnym
kondensatorze
c) dowolna ilość szeregowo połączonych kondensatorów można zastąpić jednym.
Zamiana ta nie może spowodować zmiany napięcia całkowitego U i ładunku
zgromadzonego w układzie. Pojemność zastępczego kondensatora, czyli pojemność
zastępczą Cz obliczamy ze wzoru:
Cechy charakterystyczne połączenia rrównoległego:, (jeżelinie wiesz jak wygląda
połączenie równolegle zajrzyj na stronę o rezystorach)
a) napięcie na każdym z kondensatorów jest jednakowe
b) ładunek całkowity jest suma ładunków na poszczególnych kondensatorach
c) dowolna ilość równolegle połączonych kondensatorów można zastąpić jednym,
nie może zmienić się napięcie U i ładunek układu. Pojemność zastępczą Cz
obliczamy ze wzoru:
Cz = C1 + C2 + C3 ...
Połączenie mieszane to takie, w którym występuję łączenie równolegle i
szeregowe.
Kondensator składa się z dwóch płytek przewodzących prąd elektryczny (elektrod),
które są od siebie oddalone. Może on zostać naładowany ładunkiem elektrycznym.
O zdolności magazynowania ładunku, czyli o pojemności kondensatora decyduje
powierzchnia elektrod i odległość miedzy nimi. Większą powierzchnia i mniejsza
odległość, daje wyższą pojemność.
W celu zmniejszenia odstępu miedzy elektrodami, stosuje się na izolatory
materialny, które można wykonać w formie bardzo cienkiej folii np., tworzywa
sztuczne, ceramikę lub warstwy tlenków. Materiały te charakteryzują się cecha
fizyczna nazywana przenikalnością elektryczna. Ujawnia się ona, gdy atomy
umieszczone w polu elektrycznym ulegają polaryzacji w wyniku odkształcenia
orbit elektronów na zewnętrznych powłokach. Powstają tak zwane dipole, które
mogą się obracać i przyjmować ten sam kierunek, jaki ma pole elektryczne. W
efekcie tego, zmniejsza się wpływ odległości miedzy elektrodami i pojemność
wzrasta. Ta cecha powoduje, ze materiał izolacyjny nazywa się dielektrykiem.
Czynnikiem, który w największym stopniu wpływa na pojemność kondensatora,
poza powierzchnia i odległością elektrod, jest zdolność dielektryka (w ujęciu
makroskopowym) do przyjęcia ujemnego ładunku w pobliże dodatniej elektrody, i
dodatniego ładunku w pobliże elektrody ujemnej, co powoduje ze wpływ
odległości miedzy elektrodami zmniejsza się.
W celu obliczenia pojemności kondensatora, korzystamy z następującej zależności:
C = x A/d
gdzie C = pojemność w faradach,
A = powierzchnia w m2,
d = odstęp miedzy elektrodami w m,
= przenikalność, która właściwie jest iloczynem o x r gdzie o jest
przenikalnością próżni, i wynosi 8,85 x 10-12 a r jest liczba względna, która
określa przenikalność dielektryka w stosunku do przenikalności w próżni r
nazywana jest często stałą dielektryczna lub liczba pojemnościowa.
Z tego wynika, ze wybór dielektryka w decydującym stopniu wpływa na
pojemność kondensatora i jego wymiary. Istnieją jednak inne cechy (zalety i wady)
materiałów, które powodują, ze nie zawsze można stosować materiał o najwyższej
stałej dielektrycznej.
Kilka przykładów zastosowania kondensatorów:
Jako kondensator sprzęgający, blokujący napięcie stale, ale przepuszcza dalej
napięcie zmienne. Jako kondensator blokujący, zwierający napięcie zmienne, które
występuję razem z napięciem stałym.
W filtrach i obwodach rezonansowych, gdzie najczęściej wspólnie z elementem
indukcyjnym lub rezystorem, stanowi obwód rezonansowy lub obwód filtra np., w
oscylatorze albo filtrze separującym głośnika.
Np. w zasilaczu sieciowym znajdują się kondensatory do magazynowania energii,
która jest używana do filtrowania (wygładzania) napięcia stałego.
W obwodach czasowych wykorzystuje się ładowanie i rozładowywanie
kondensatora do określenia czasu. Przykładem tego jest multiwibrator astabilny.
Jako elementu odkłócającego, używa się kondensatora, który może pochłonąć
krótkie impulsy napięcia tak np., jak w obwodzie RC przyłączonym do cewki
przekaźnika. Używa się również kondensatorów np. typu X lub Y w celu tłumienia
zakłóceń o wysokich częstotliwościach (RFI). Przy paradach zmiennych wysokiego
napięcia, używa się często do pomiarów pojemnościowych dzielników napięcia.
Nie maja one takich dużych strat jak rezystancyjne dzielniki napięcia.
Kondensator, przy przepływie prądu zmiennego, stanowi opór zależny od
częstotliwości, który jest nazywany reaktancja pojemnosciowa (Xc).
Xc = 1/( x C)
gdzie Xc = reaktancja ,
m = pulsacja (2 x x f) w Hz,
C = pojemność w faradach.
Energie, która można magazynować w kondensatorze wylicza się ze wzoru:
E = 1/2 x C x U2
gdzie E = energia w kondensatorze w joulach (Ws),
C = pojemność w faradach,
U = napięcie w voltach.
Pod pojęciem pojemności C, rozumie się zdolność kondensatora do przyjęcia
ładunku Q w coulombach, na volt przyłożonego napięcia U. Jest to opisane
wzorem :
C=Q/U
Jednostka pojemności jest farad, który ma wymiar A x s/V. Pojemność 1 farada
posiada kondensator, w którym ładunek 1 coulomba powoduje powstanie napięcia
1 volta.
Naładowanie i rozładowanie kondensatora zajmuje zawsze pe- wien czas. Zmiany
ładunku wiążą się z kolei z przepływem prądu przez jakąś rezystancje. Najniższą
rezystancja to rezystancja doprowadzeń elektrod. Przez stałą czasowa rozumiemy
czas, który jest potrzebny żeby ładunek osiągnął 63,2% (1- e-1) maksymalnego
napięcia.
=RxC
gdzie podany jest w sekundach o ile R podane jest w , a C w faradach.
Przyjmuje się, ze kondensator jest całkowicie naładowany, po czasie 5 x
Przebieg ćwiczenia
1. Schemat połączeń:
a) Dla pojedynczych kondensatorów C1 i C2
b) Dla szeregowo połączonych kondensatorów.
c) Dla równolegle połączonych kondensatorów.
2. Wyniki pomiarów:
a)
Lp
1
2
3
4
5
Śr
X1
C
f
Hz
50
50
50
50
50
-
U1
V
60
90
120
150
192
-
I1
mA
420
700
850
1040
1340
-
X1
KΩ
0,13
0,14
0,14
0,14
0,14
0,14
C1
µF
24,78
22,1
22,2
22,6
22,3
22,8
f
Hz
50
50
50
50
50
-
U1
V
60
98
120
140
192
-
I1
mA
74
115
140
160
230
-
X1
KΩ
0,81081
0,85217
0,85714
0,875
0,83478
0,84598
C1
µF
3,93
3,74
3,72
3,64
3,82
3,77
U1
I1
I
2 f X c
b)
Lp
1
2
3
4
5
Śr
U
X1 1
I1
C
I
2 f X c
c)
Lp
1
2
3
4
5
Śr
X1
f
Hz
50
50
50
50
50
-
U1
V
148
176
192
212
226
-
I1
mA
150
170
190
210
220
-
X1
KΩ
0,98667
1,03529
1,01053
1,00952
1,02727
1,01386
C1
µF
3,23
3,08
3,15
3,15
3,1
3,14
U1
V
26
40
60
76
100
-
I1
mA
230
340
500
650
850
-
X1
KΩ
0,11304
0,11765
0,12
0,11692
0,11765
0,11705
C1
µF
28,17
27,07
26,54
27,24
27,07
27,22
U1
I1
I
2 f X c
1
1
1
C C2 śr
śr1
Cśr Cśr1 C2 r1 Cśr1 C2 śr
C
C
Cśr1 C2 śr
Cśr1 C2 śr
C
22,8 3,77
3,2F
22,8 3,77
d)
Lp
1
2
3
4
5
Śr
X1
f
Hz
50
50
50
50
50
-
U1
I1
I
2 f X c
Cśr C1śr C2 śr
C
Cśr 22,8 3,77 26,6
3. Wnioski:
Celem ćwiczenia było poznanie metody technicznej pomiaru pojemności (metody
woltomierza i amperomierza), sprawdzenia słuszności wzorów do obliczania pojemności
zastępczej, a także doskonalenia umiejętności posługiwania się miernikami analogowymi i
cyfrowymi w praktyce pomiarowej.
Do wykonywania pomiarów w tym ćwiczeniu zastosowałem metodę z poprawnie
mierzonym napięciem. Postąpiłem tak dlatego, ponieważ reaktancja pojemnościowa
badanych kondensatorów jest znacznie mniejsza od pierwiastka iloczynu oporności
wewnętrznych zastosowanych w tym ćwiczeniu mierników. Dzięki zastosowaniu tej właśnie
metody wyniki pomiarów pojemności będą miały mniejsze uchyby, będą bardziej miarodajne.