18.1 Jednorodne pole elektryczne. Mówimy, że w danym obszarze

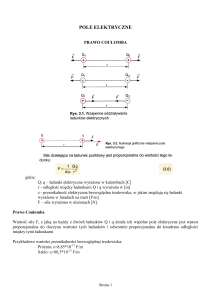
18.1 Jednorodne pole elektryczne.
Mówimy, że w danym obszarze istnieje jednorodne pole
elektryczne, jeżeli w każdym punkcie tego obszaru
wartość natężenia pola jest jednakowa. Jednorodne pole
elektryczne wytwarzamy na przykład między okładkami
kondensatora płaskiego.
Kondensator płaski tworzą dwie równoległe naładowane
płyty metalowe (każda z płyt ma ładunek przeciwny do
drugiej).
Linie sił pola jednorodnego są wzajemnie równoległe.
W jednorodnym polu elektrycznym zależność między
natężeniem pola elektrycznego a różnicą potencjałów
wyraża się wzorami:
lub
gdzie:
ΔV - różnica potencjałów płyt kondensatora, czyli inaczej napięcie (U),
d - odległość płyt kondensatora.
Jeśli chciał(a)byś dowiedzieć się, jak wyprowadzić taki wzór, kliknij w link "Kondensator
- natężenie pola" znajdujący się poniżej.
Zobacz też: Natężenie pola elektrostatycznego Potencjał elektrostatyczny Kondensator - natężenie pola Zadanie
3 Zadanie 4 Zadanie 16 Zadanie 17
do góry
18.2 Pojemność elektryczna.
Jeżeli dostarczymy ładunek Q odizolowanemu przewodnikowi, to wzrasta również jego
potencjał elektryczny V, przy czym wzrost potencjału jest proporcjonalny do
dostarczonego ładunku. Stosunek tego ładunku do potencjału przewodnika, nazywamy
pojemnością elektryczną C, co wyrażamy wzorem:
Jednostką pojemności jest farad (F).
1 Farad to taka pojemność przewodnika, w którym dostarczenie ładunku 1 kulomba
powoduje wzrost potencjału o 1 wolt.
Farad jest bardzo dużą pojemnością (Ziemia ma pojemność dużo mniejszą niż 1F),
dlatego najczęściej używamy jednostek pojemności mniejszych:
1 mikrofarad (µF) = 10-6F
1 nanofarad (nF) = 10-9F
1 pikofarad (pF) = 10-12F = 10-6µF
Zobacz też: Potencjał elektrostatyczny Zadanie 5
do góry
18.3 Pojemność kondensatora.
Kondensator jest układem przewodników służącym do gromadzenia ładunków
elektrycznych. Istnieją różnego typu kondensatory, ale my ograniczymy się do
omawiania tylko kondensatora płaskiego. Stanowią go dwie wzajemnie odwzorowane
płyty metalowe (okładki), a jego pojemność możemy obliczyć ze wzoru:
gdzie:
S - powierzchnia czynna okładek,
d - odległość między okładkami kondensatora,
ε0 - przenikalność elektryczna próżni (stała),
εR - względna przenikalność elektryczna dielektryka wypełniającego przestrzeń między
okładkami (liczba niemianowana).
Dla kondensatora próżniowego εR = 1.
Dielektryk (εR > 1) zwiększa pojemność kondensatora εR razy.
Pojemność kondensatora płaskiego możemy również obliczyć korzystając ze wzoru na
pojemność elektryczną, przy czym potencjał elektryczny zastępujemy różnicą
potencjałów, czyli napięciem:
Jeśli interesujesz się tym, jak wyprowadzić powyższe wzory, kliknij poniżej na temat
"Kondensator - pojemność elektryczna".
Zobacz też: Kondensator - pojemność elektryczna Zadanie 7 Zadanie 11 Zadanie 12 Zadanie 13 Zadanie 14
do góry
18.4 Inne właściwości kondensatorów.
Siła wzajemnego przyciągania się okładek:
Na okładkach naładowanego kondensatora znajdują się ładunki przeciwnych znaków,
dlatego też okładki te przyciągają się wzajemnie. Jeżeli przez Q oznaczymy ładunek
zgromadzony na jednej z okładek, zaś E oznaczać będzie natężenie pola elektrycznego
między okładkami kondensatora, to siłę F wzajemnego przyciągania się okładek wyraża
się wzorem:
Energia kondensatora:
W kondensatorze o pojemności C, naładowanym do napięcia U, zgromadzona jest
energia:
Ponieważ Q = CU, to alternatywne wzory na energię wynoszą:
Energię naładowanego kondensatora wykorzystujemy między innymi w elektronicznych
lampach błyskowych, używanych w aparatach fotograficznych, w których naładowany
kondensator rozładowuje się przez palnik lampy wypełnionej ksenonem.
Zobacz też: Skutki rozsuwania okładek kondensatora Zadanie 2 Zadanie 9 Zadanie 10 Zadanie 12 Zadanie 15
Zadanie 16
do góry
18.5 Łączenie kondensatorów.
szeregowe
równoległe
Zobacz też: Zadanie 1 Zadanie 8 Zadanie 11 Zadanie 12 Zadanie 15
do góry
18.6 Dielektryk w polu elektrycznym.
Dielektryk to ciało, w którym ładunki nie mogą się przemieszczać, nie posiada więc
swobodnych elektronów. Elektrony znajdujące się w izolatorach są związane z atomami i
cząsteczkami. Gdy dielektryk znajdzie się w polu elektrostatycznym, może zachodzić
przemieszczanie się elektronów, ale tylko w obrębie cząsteczki. Np. gdy dielektryk jest
między płytkami naładowanego kondensatora, elektrony chcą się znaleźć możliwie blisko
płytki dodatniej. Cząsteczka staje się tzw. dipolem elektrycznym, czyli układem dwóch
ładunków o jednakowej wartości i o przeciwnych znakach. Jeżeli dielektryk ma dipolową
budowę cząsteczek w nieobecności pola elektrostatycznego zewnętrznego, to w polu
naładowanego kondensatora zachodzi uporządkowywanie się tych cząsteczek - dipoli.
Dielektryk o niedipolowej budowie
Dielektryk o niedipolowej budowie
cząsteczek w nieobecności pola
cząsteczek w obecności pola zewnętrznego
zewnętrznego ma cząsteczki z równomierniema cząsteczki z uporządkowanymi
rozłożonymi ładunkami.
ładunkami - dipolami.
W dielektryku o dipolowej budowie
W dielektryku o dipolowej budowie
cząsteczek cząsteczki - dipole w
cząsteczek cząsteczki - dipole w obecności
nieobecności zewnętrznego pola są ułożone pola zewnętrznego są uporządkowane.
chaotycznie.
W jednym i w drugim rodzaju dielektryków w obecności zewnętrznego pola
elektrostatycznego dochodzi do porządkowania cząsteczek - dipoli. Jest to tzw.
polaryzacja dielektryka. W spolaryzowanym dielektryku powstaje jego własne pole
elektrostatyczne. To wewnętrzne pole w dielektryku jest zwrócone zawsze przeciwnie do
pola zewnętrznego. Dlatego też dochodzi do osłabienia pola wypadkowego, czyli do
zmniejszenia natężenia.
Ponieważ ładunek na płytkach kondensatora nie zmienia się wskutek wsunięcia między
płytki dielektryka, napięcie między płytkami maleje (E = U / d). Na podstawie definicji
pojemności kondensatora (C = Q / U) widzimy, że przy stałym ładunku, a malejącym
napięciu, włożenie między płytki dielektryka zwiększa pojemność kondensatora.
Iloraz pojemności kondensatora z dielektrykiem do pojemności tego kondensatora, gdy
między płytkami jest próżnia, jest miarą względnej przenikalności dielektrycznej
środowiska, zwanej też stałą dielektryka.
C - pojemność kondensatora z dielektrykiem między płytkami
C0 - pojemność kondensatora z próżnią między płytkami