Document

E5. KONDENSATOR W OBWODZIE PRĄDU STAŁEGO
I DRGANIA RELAKSACYJNE
tekst opracował: Marek Pękała
Główna część ćwiczenia koncentruje się na badaniu rozładowania kondensatora.
Badanie drgań relaksacyjnych potwierdza asystent.
Procesy rozładowania kondensatora i drgania relaksacyjne w obwodach RC należą do
szerokiej klasy procesów relaksacyjnych. Procesy relaksacyjne przeprowadzają układ do
stanu równowagi trwałej lub nietrwałej o niższej energii a dokładniej o niższym potencjale
termodynamicznym. Procesy relaksacyjne są procesami nieodwracalnymi, w których
następuje częściowa dyssypacja (rozproszenie) energii poprzez zamianę jej na ciepło.
Szybkość
procesów
y
 dy 
relaksacyjnych
jest y
 
0
 dt 
t
 

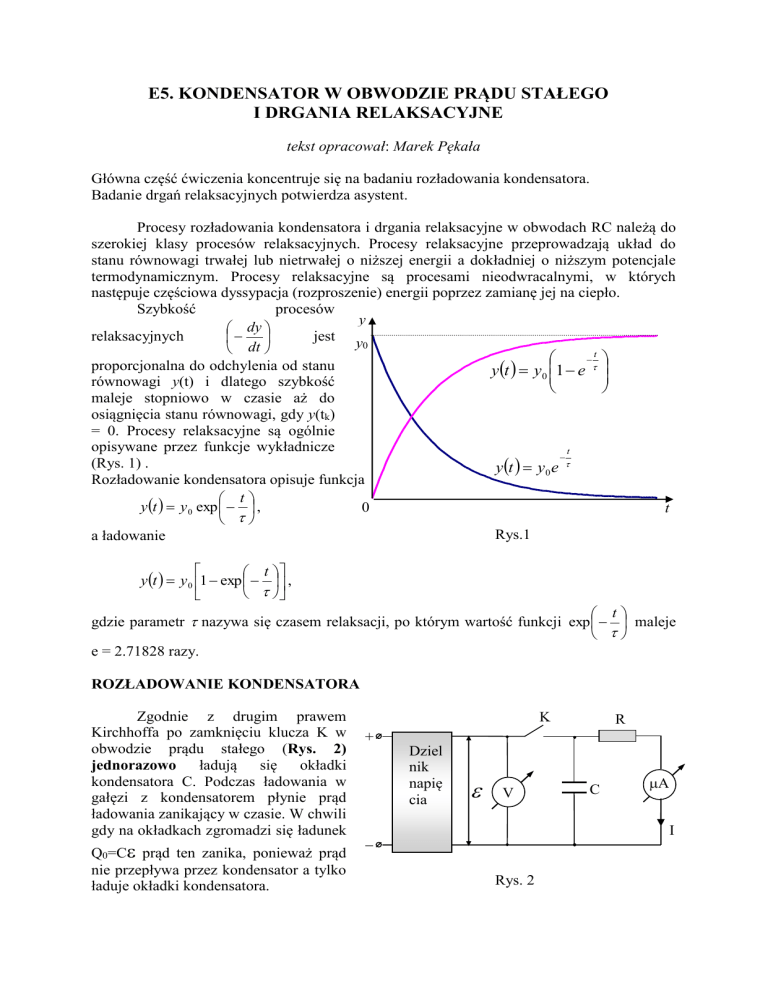
proporcjonalna do odchylenia od stanu

y t   y0 1  e 
równowagi y(t) i dlatego szybkość


maleje stopniowo w czasie aż do
osiągnięcia stanu równowagi, gdy y(tk)
= 0. Procesy relaksacyjne są ogólnie
opisywane przez funkcje wykładnicze
t

(Rys. 1) .
y t   y 0 e 
Rozładowanie kondensatora opisuje funkcja
 t
y t   y 0 exp    ,
0
t
 
x
Rys.1
a ładowanie

 t 
y t   y 0 1  exp    ,
  

 t
gdzie parametr  nazywa się czasem relaksacji, po którym wartość funkcji exp    maleje
 
e = 2.71828 razy.
ROZŁADOWANIE KONDENSATORA
Zgodnie z drugim prawem
Kirchhoffa po zamknięciu klucza K w
obwodzie prądu stałego (Rys. 2)
jednorazowo ładują się okładki
kondensatora C. Podczas ładowania w
gałęzi z kondensatorem płynie prąd
ładowania zanikający w czasie. W chwili
gdy na okładkach zgromadzi się ładunek
Q0=C prąd ten zanika, ponieważ prąd
nie przepływa przez kondensator a tylko
ładuje okładki kondensatora.
K
R
+
Dziel
nik
napię
cia

V
C
A
I

Rys. 2
2
Wtedy przez opornik R przepływa prąd stały o natężeniu I 
.
Po otwarciu klucza
R
odłączona zostaje siła elektromotoryczna i w prawej części układu następuje rozładowanie
kondensatora przez opornik R i rozproszenie energii. Zgodnie z drugim prawem Kirchhoffa
Q
 IR  0
(1)
C
Q
gdzie
i IR opisują chwilowe spadki napięcia odpowiednio na kondensatorze C i na
C
dQ
oporniku R. Uwzględniając, że I 
ostatnie równanie można zapisać
dt
Q
dQ
R
 0.
(2)
C
dt
Po rozdzieleniu zmiennych
dQ
1

dt
Q
RC
oznaczając iloczyn RC =  po scałkowaniu otrzymujemy rozwiązanie
 t
 t
Qt   Q0 exp     C exp   
 
 

(3)
(4)
opisujące chwilowe wartości ładunku na kondensatorze w funkcji czasu. Chwilowe wartości
napięcia na kondensatorze opisuje
Q
 t
 t
U t   0 exp     exp   
(5)
C
 
 
Uwzględniając prawo Ohma

I t  
 exp   t   I
R
 
0
 t
exp   
 
(6)
otrzymujemy funkcję wykładniczą opisująca natężenie prądu rozładowania kondensatora w
obwodzie RC.
DRGANIA RELAKSACYJNE
Drgania relaksacyjne powstają w tzw. układzie prądu stałego RC, czyli w układzie
RC zasilanym ze źródła stałej siły elektromotorycznej SEM (Rys. 3), w którym równolegle
do kondensatora C połączony jest tzw. element kluczący, czyli pełniący rolę automatycznego
klucza elektrycznego, w postaci półprzewodnikowego diaka lub neonówki.
3
R
+

Dzielnik
napięcia
C
Diak
Sonda
oscyloskopu

Rys.3
Opór elektryczny diaka jest funkcją przyłożonego napięcia i pozwala kontrolować procesy
ładowania i rozładowania kondensatora C. Poniżej tzw. napięcia progowego UP opór diaka
jest duży (rzędu M) a maleje gwałtownie o kilka rzędów wielkości po przekroczeniu UP ,
gdy diak przechodzi w stan przewodzenia. W stanie przewodzenia prądu opór elektryczny
diaka pozostaje mały aż do napięcia gaśnięcia UG prawie równego zeru (Rys. 4). W
obwodzie RC dokonują się wtedy drgania relaksacyjne napięcia UC pomiędzy napięciem
progowym UP a napięciem gaśnięcia UG.
U

UP
UG
t1
t
t2
T
Rys.4
Gdy opór elektryczny diaka jest duży, następuje ładowanie kondensatora C przez
opornik R i zgodnie z drugim prawem Kirchhoffa
Q
 IR   0
(7)
C
czyli
dQ Q
R
 0
(8)
dt C


Zatem rozwiązaniem równania różniczkowego
4

dQ
1
 dt
Q R

C
(9)
jest funkcja
Q
 C 1  exp   RCt  .



Napięcie na kondensatorze zapiszemy
UC 
 1  exp  RCt 


(10)

Rys.4 pokazuje, że ładowanie kondensatora od zera (UC(0) = 0) do napięcia
UG = UG(t) następuje po czasie t. Analogicznie ładowanie kondensatora od zera (UC(0) = 0)
do napięcia UP = UP(t + t1) następuje po czasie t +t 1. Oba przypadki opisują równania

 t 
(11)
U G  U G t   1  exp  

 RC 


U P  U P t  
 t 
 1  exp  tRC

1



(12)
Przekształcając równania do postaci
  U   exp   RCt 
(13)
 U  
(14)
G
P


 t  t1 
exp  

 RC 
następnie dzieląc stronami i logarytmując otrzymujemy czas ładowania t1
t1  RC ln
 U
 U
G
(15)
P
Ponieważ napięcie gaśnięcia diaka jest bliskie zera, ostatnie równanie upraszcza się do
t1  RC ln

 U
 RC  const
(16)
P
Po przekroczeniu napięcia progowego diaka UP rozpoczyna się rozładowanie
kondensatora przez przewodzący diak. Zmiany napięcia UC(t) podczas rozładowania
kondensatora C od napięcia UP = UP(t) do napięcia gaśnięcia UG = UG (t + t2) można zapisać
jako

t2 
 ,
(17)
U G  U P exp  
 RDIAKC 
gdzie RDIAK jest oporem diaka w stanie przewodzenia. Wtedy czas rozładowania
kondensatora t2 jest równy
5
U 
t 2  RDIAKC ln  P  .
UG 
Ostatecznie okres drgań relaksacyjnych T jest sumą
T = t1 + t2
(18)
(19)
Jeżeli t1 >> t2, to T  t1 .
Cel
Celem ćwiczenia jest doświadczalne wyznaczenie i analiza parametrów opisujących
rozładowanie kondensatora, takich jak:
 krzywa rozładowania, czyli zależność I(t);
 ładunek naładowanego kondensatora wyznaczony z krzywej rozładowania;
 energia naładowanego kondensatora;
 stała czasowa obwodu i opór rozładowania;
oraz drgania relaksacyjne, takich jak:
 okres drgań relaksacyjnych dla różnych napięć i pojemności;
 opór, przez który ładuje się kondensator.
Wymagania
Przewodniki i dielektryki.
Pole elektryczne: linie sił, natężenie, potencjał, napięcie, praca, energia.
Źródła pola elektrycznego, dipol elektryczny.
Indukcja elektryczna, polaryzacja dielektryków.
Kondensator, pojemność elektryczna
Obwód RC, ładowanie i rozładowanie kondensatora, stała czasowa., drgania
relaksacyjne.
Prawa Ohma i Kirchhoffa, siła elektromotoryczna,.
Mierniki prądu i napięcia, dzielnik napięcia .
Budowa i zasada działania półprzewodnikowego diaka, neonówki i oscyloskopu
Literatura
R. Resnick, D. Halliday – Fizyka t.2; D. Halliday, R. Resnick, J. Walker – Fizyka t.3; E. EM
E. M Purcell – Elektryczność i magnetyzm; tom II
H. Szydłowski, Pracownia fizyczna;
A. Piekara, Elektryczność i magnetyzm, PWN
K. Zboiński – Laboratorium z fizyki;
R. Nowak - Statystyka dla fizyków, PWN 2002 + ćwiczenia.
Opis układu
Układ pomiarowy do badania prądu rozładowania kondensatora składa się z zasilacza
napięcia stałego, opornika, kondensatora dekadowego i mikroamperomierza. Czas mierzy się
stoperem.
W układzie do badania drgań relaksacyjnych równolegle do kondensatora włącza się
diak i zmiany napięcia na kondensatorze obserwuje się na oscyloskopie połączonym sondą z
układem.
6
Wykonanie ćwiczenia
Rozładowanie kondensatora
Uwaga: napięcie zasilania włącza asystent.
Krzywą rozładowania kondensatora tworzy się mierząc chwilowe wartości natężenia prądu
rozładowania kondensatora I(t).
1. Przed rozpoczęciem pomiarów należy tak wypoziomować galwanometr, żeby
wskaźnik znalazł się na zerze.
2. Korzystając z płytki montażowej łączymy obwód według schematu
przedstawionego na rysunku 2. Do układu pomiarowego włączamy kondensator
dekadowy wybierając pojemność elektryczną C = 1 F.
3. Sprawdzamy czy napięcie ustawione na zasilaczu stabilizowanym IZS 5/71
wynosi 100V.
4. Po sprawdzeniu obwodu przez asystenta i włączeniu zasilania ustawienie
dzielnika napięcia wybieramy tak, żeby początkowe natężenie prądu rozładowania
I0 mierzone galwanometrem było równe 10 A.
5. Zapisujemy napięcie  odczytane z woltomierza.
6. Otwierając klucz mierzymy kilkakrotnie czas, w ciągu którego natężenie prądu
maleje od początkowej wartości I0 = 10 A do wartości Ik zmieniającej się co
1 A od 9 A do 0 A.
7. Następne pomiary krzywej rozładowania (jak w 6) wykonuje się dla Ci = 2 i 3 F
oraz dla nieznanego kondensatora CX.
Badanie drgań relaksacyjnych
1. Korzystając z odpowiedniej płytki montażowej łączymy obwód według schematu
przedstawionego na rysunku 3. Do układu pomiarowego włączamy opornik Rx i
kondensator dekadowy, wybierając pojemność elektryczną C = 0,01 F. Za
pomocą sondy oporowej, osłabiającej sygnał w stosunku 1:10, napięcie panujące
na kondensatorze podajemy na kanał 1 oscyloskopu.
2. Sprawdzamy czy napięcie ustawione na zasilaczu stabilizowanym IZS 5/71
wynosi 100V.
3. Po sprawdzeniu obwodu przez asystenta i włączeniu zasilania regulujemy
napięcie dzielnikiem i ustawiamy na 35V. Na ekranie oscyloskopu obserwujemy
periodyczne zmiany napięcia. Przy wciśniętym klawiszu MEASURE po prawej
stronie ekranu wyświetlane są wartości okresu (PERIOD), częstotliwości
(FREQ.), wartości średniej napięcia (MEAN) i wartości szczytowej (Pk –Pk)
4. Zmniejszając napięcie znajdujemy napięcie przebicia diaka. Zapisujemy wartość
Up.
5. Zmieniając pojemność od 0,01 do 0,1F mierzymy zależność okresu drgań
relaksacyjnych przy 2 różnych napięciach  np. 35V i 50V.
Uwaga: napięcie przykładane do diaka nie powinno przekraczać 50V.
6. Mierzymy zależność okresu drgań relaksacyjnych od napięcia  (od 35V do 50V
co ok. 1,5 V) przy 2 różnych pojemnościach kondensatora np.0,03F i 0,08F.
7
Sprawozdanie - Opracowanie wyników
I.
II.
III.
IV.
Cel ćwiczenia
Krótki opis metody pomiarowej
Krótki, ogólny opis analizy wyników pomiarowych – zależności
matematyczne
Opracowanie wyników
Krzywa rozładowania
a) Dla każdego zbioru wyników doświadczalnych I(t) dla danej pojemności C
wykonujemy wykresy krzywej rozładowania kondensatora I(t) na papierze
milimetrowym lub stosując programy komputerowe.
b) Obliczamy pola powierzchni pod krzywymi I(t) metodą graficzną* lub wagową**.
* Metoda graficzna - (H. Szydłowski - Pracownia fizyczna, PWN) - Pole
ograniczone przez oś czasu - t, oś prądu - I oraz krzywą rozładowania - I(t) dzielimy
na przybliżone trapezy o podstawach równoległych do osi pionowej i obliczamy sumę
pól trapezów. (Jeżeli trapezy mają równe wysokości, obliczenie upraszcza się poprzez
odpowiednie (!) sumowanie połówek podstaw trapezów.)
** Metoda wagowa - Wycinamy pole ograniczone przez oś czasu -t, oś prądu -I oraz
krzywą rozładowania I(t). Z tego samego papieru wycinamy też, np. 1 dcm2.
Porównanie wagi obu wycinków pozwala określić powierzchnię pod krzywą I(t).
Uwzględniając, jakiemu ładunkowi elektrycznemu odpowiada, np. 1 cm2 na wykresie,
obliczamy ładunek zgromadzony na kondensatorze – Q .
(Wpływ niedokładności wynikającej z sumowania elementów powierzchni pod
krzywą I(t) dla t  , można ograniczyć biorąc pod uwagę, że po czasie, np. t = 3  (
= stała czasowa) z kondensatora odpływa 95 % ładunku).
c) Energię zgromadzoną w kondensatorze E ± E obliczamy jako E = Q2/2C.
d) W celu sprawdzenia, że natężenie prądu rozładowania kondensatora maleje
 t
 t 
eksponencjalnie w czasie zgodnie z wyrażeniem I t   I 0 exp     I 0 exp  

 
 RC 
I t 
 t
logarytmujemy obustronnie wyrażenie
 exp    i otrzymujemy liniową
I0
 
 I (t ) 
1
1
   t   At , gdzie A  . Z danych doświadczalnych
funkcję czasu ln 


 I0 
 I t  
 i wykonujemy wykres w zależności od czasu t. Wykres można
obliczamy ln 
 I0 
wykonać stosując programy komputerowe.
e) Po zaznaczeniu błędów na wykresie obliczamy współczynnik nachylenia tego
wykresu oraz błąd współczynnika nachylenia A ± A metodą najmniejszych
kwadratów.
f) Obliczamy stałą czasową  ±  dla każdej pojemności kondensatora.
(Stałą czasową  ±  można także wyznaczyć z wykresu stycznej do wykresu I(t) w
dowolnym punkcie ts. Warto zauważyć, że dla dowolnego czasu ts, odcinek na osi
odciętych Δt = tw - ts zawarty między rzutem punktu styczności ts na oś t, a punktem tw
przecięcia stycznej z osią t, ma długość τ).
8
g) Wykonujemy wykres stałej czasowej  w funkcji pojemności kondensatora.
h) Przy pomocy stałej czasowej  ±  i pojemności kondensatorów C obliczamy opór
elektryczny R ± R, przez który rozładowuje się kondensator.
i) Pojemność nieznanego kondensatora CX ± CX można obliczyć przy pomocy stałej
czasowej  X ± X i wyznaczonego w punkcie h) oporu R ± R.
j) Błędy obliczamy metodą propagacji niepewności uwzględniając dokładność/błąd
pomiaru/odczytu zmierzonych parametrów.
k) Wyniki zbieramy w tabeli podając ładunek naładowanego kondensatora Q  Q,
ładunek obliczony Q = UC, współczynnik nachylenia A ± A, opór rozładowania R ±
R, pojemność nieznanego kondensatora CX ± CX.
l) Jeżeli poprzednie wyniki nie zostały opatrzone odpowiednim komentarzem,
sprawozdanie kończymy podsumowującymi wnioskami i porównaniem z
przewidywaniami.
Drgania relaksacyjne
a) Wykonujemy wykresy okresu drgań relaksacyjnych T w funkcji pojemności C
kondensatora dla różnych napięć . Wykresy można wykonać stosując programy
komputerowe.
b) Po zaznaczeniu błędów T i C obliczamy współczynniki nachylenia B  B
wykresów T(C) dla różnych napięć .
c) Przy pomocy współczynników nachylenia B, napięcia progowego diaka UP oraz
przyłożonego napięcia
kondensator.
 obliczamy opór elektryczny R  R, przez który ładuje się
 ε 
.
d) Wykonujemy wykres okresu drgań relaksacyjnych T w funkcji ln 
   U p 


   

  obliczamy współczynniki nachylenia
e) Uwzględniając błędy T i  ln 


    U p  

 
  
.
D  D wykresów T w funkcji ln 
   U p 


f) Przy pomocy pojemności kondensatora C i współczynnika nachylenia D  D
obliczamy opór elektryczny R  R, przez który ładuje się kondensator i
porównujemy z punktem c).
g) Jeżeli poprzednie obliczenia, wykresy i ewentualnie tabele nie zostały opatrzone
odpowiednim komentarzem, sprawozdanie kończymy podsumowującymi
wnioskami.
h) Jaki warunek powinny spełniać opory R1 i R2, aby czasy ładowania i rozładowania
były równe ?