3. Reprezentacje znaków w komputerze

3. Reprezentacje znaków w komputerze
Wszelkie informacje przetwarzane w komputerze są ciągam bitów. Dlatego każdy znak wprowadzany z klawiatury (np.
A, a, 7, %, !), każda liczba (np. 17; 5,(3); -8), dźwięk, obraz muszą być zapisane jako sekwencje 0-1. W zależności od typu
znaku, przyjęte są różne umowy co do ich kodowania, czyli zamiany na reprezentację binarną.
3.1. Znaki alfanumeryczne
Znaki alfanumeryczne to znaki, które mogą być wprowadzone za pomocą klawiatury komputera, czyli oprócz cyfr 0-9,
liter a-Z również znaki interpunkcyjne, symbole matematyczne i znaki specjalne, np.: ";", "+", "(", "#", "!", "@".
Uwzględnione są również specyficzne znaki stosowane w alfabetach różnych języków, takie jak: "ą", "é", "ç".
Najpopularniejszymi standardami kodowania są:
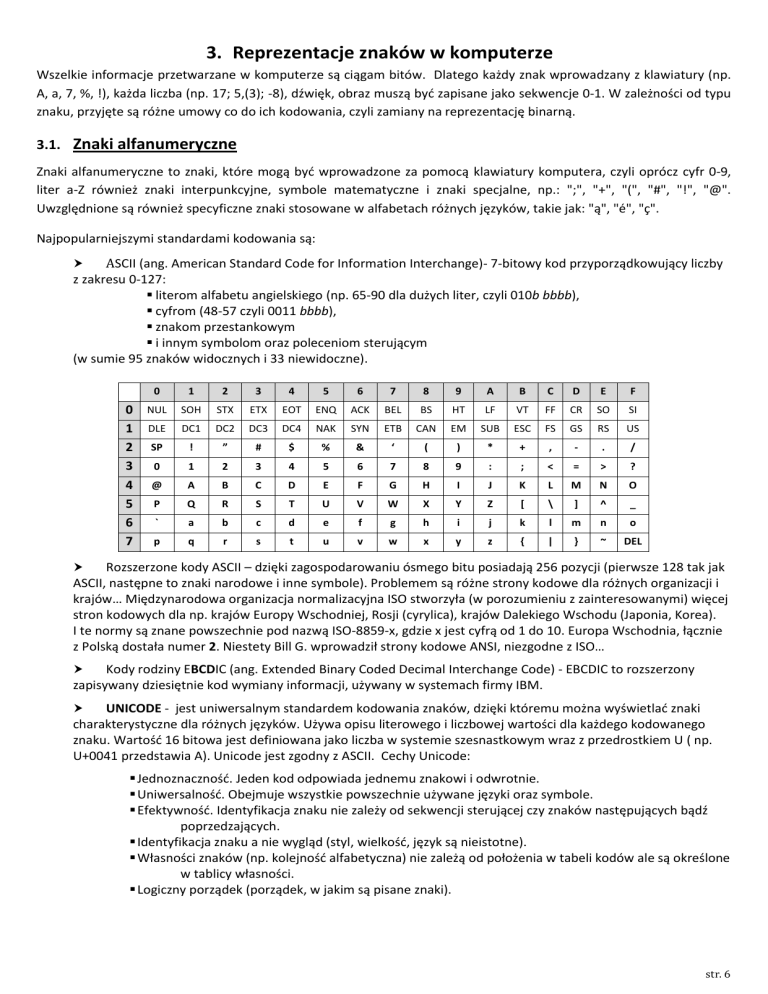
ASCII (ang. American Standard Code for Information Interchange)- 7-bitowy kod przyporządkowujący liczby
z zakresu 0-127:
 literom alfabetu angielskiego (np. 65-90 dla dużych liter, czyli 010b bbbb),
 cyfrom (48-57 czyli 0011 bbbb),
 znakom przestankowym
 i innym symbolom oraz poleceniom sterującym
(w sumie 95 znaków widocznych i 33 niewidoczne).

0
0 NUL
1 DLE
2 SP
3 0
4 @
5 P
`
6
7 p
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
SOH
STX
ETX
EOT
ENQ
ACK
BEL
BS
HT
LF
VT
FF
CR
SO
SI
DC1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
!
”
#
$
%
&
‘
(
)
*
+
,
-
.
/
1
2
3
4
5
6
7
8
9
:
;
<
=
>
?
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
Q
R
S
T
U
V
W
X
Y
Z
[
\
]
^
_
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
q
r
s
t
u
v
w
x
y
z
{
|
}
~
DEL

Rozszerzone kody ASCII – dzięki zagospodarowaniu ósmego bitu posiadają 256 pozycji (pierwsze 128 tak jak
ASCII, następne to znaki narodowe i inne symbole). Problemem są różne strony kodowe dla różnych organizacji i
krajów… Międzynarodowa organizacja normalizacyjna ISO stworzyła (w porozumieniu z zainteresowanymi) więcej
stron kodowych dla np. krajów Europy Wschodniej, Rosji (cyrylica), krajów Dalekiego Wschodu (Japonia, Korea).
I te normy są znane powszechnie pod nazwą ISO-8859-x, gdzie x jest cyfrą od 1 do 10. Europa Wschodnia, łącznie
z Polską dostała numer 2. Niestety Bill G. wprowadził strony kodowe ANSI, niezgodne z ISO…

Kody rodziny EBCDIC (ang. Extended Binary Coded Decimal Interchange Code) - EBCDIC to rozszerzony
zapisywany dziesiętnie kod wymiany informacji, używany w systemach firmy IBM.

UNICODE - jest uniwersalnym standardem kodowania znaków, dzięki któremu można wyświetlać znaki
charakterystyczne dla różnych języków. Używa opisu literowego i liczbowej wartości dla każdego kodowanego
znaku. Wartość 16 bitowa jest definiowana jako liczba w systemie szesnastkowym wraz z przedrostkiem U ( np.
U+0041 przedstawia A). Unicode jest zgodny z ASCII. Cechy Unicode:
 Jednoznaczność. Jeden kod odpowiada jednemu znakowi i odwrotnie.
 Uniwersalność. Obejmuje wszystkie powszechnie używane języki oraz symbole.
 Efektywność. Identyfikacja znaku nie zależy od sekwencji sterującej czy znaków następujących bądź
poprzedzających.
 Identyfikacja znaku a nie wygląd (styl, wielkość, język są nieistotne).
 Własności znaków (np. kolejność alfabetyczna) nie zależą od położenia w tabeli kodów ale są określone
w tablicy własności.
 Logiczny porządek (porządek, w jakim są pisane znaki).
str. 6
3.2. Liczby
Kodowanie liczb opiera się na ich konwersji na system binarny. Nie mniej trzeba jeszcze pamiętać, że dana liczba zajmuje
z góry określoną liczbę bitów oraz określić jak zapisać liczby ujemne i ułamki.
3.2.1. Liczby naturalne.
Kodowanie liczby naturalnej na n-bitach polega na zapisie liczby w systemie (2) i uzupełnieniu jej od lewej strony
zerami do n pozycji.
Np. Liczba 26=11010(2) na 8 bitach:
0
0
0
1
1
0
1
0
3.2.2. Liczby całkowite.

Kod ZM (kod znak-moduł)
Wszystkie bity poza najstarszym mają takie samo znaczenie jak w naturalnym kodzie binarnym. W kodzie ZM
najstarszy bit jest bitem znaku. Jeżeli ma on wartość 0 to dana liczba jest dodatnia, jeżeli 1 to liczba jest ujemna.
W związku z tym występują dwie reprezentacje zera. Kłopotliwe jest wykonywanie działań w ZM
26 
0 0 0 1 1 0 1 0
-26 
1 0 0 1 1 0 1 0

Kod U2 (kod uzupełnień do 2)
Kodowanie U2 jest obecnie najpopularniejszą reprezentacją liczb całkowitych (oraz ułamkowych przedstawionych
w formacie stałoprzecinkowym). Operacje dodawania i odejmowania są w nim wykonywane tak samo jak dla liczb
binarnych bez znaku. Z tego też powodu oszczędza się na kodach rozkazów procesora. Liczba dodatnia całkowita
jest zapisana tak samo jak w ZM.
W kodzie U2 najstarszy bit n-bitowej reprezentacji ma wagę -2n-1, a pozostałe bity tradycyjnie kolejno +2n-2,
+2n-3,….
Algorytm zapisu liczby ujemnej w kodzie U2:
1. Zapisz liczbę przeciwną do danej tak jak w ZM.
2. Dokonaj inwersji bitów (czyli pozamieniaj 0 na 1 i odwrotnie:);
3. Zwiększ wynik o 1.
Np. Liczba -27 na 8 bitach w U2:
0 0 0 1 1 0 1 1

1. Zapisujemy liczbę 27 na 8bitach
1 1 1 0 0 1 0 0
2. Zamieniamy bity

1 1 1 0 0 1 0 1
3. Dodajemy 1 i mamy -27 w U2
Natomiast 10101001U2 = -27+(25+23+1) = -128+41 = -87
3.2.3. Liczby rzeczywiste.

Zapis stałopozycyjny.
Do zapisu liczby stałoprzecinkowej przeznaczona jest z góry określona ilość bitów, a pozycję przecinka ustala się
arbitralnie, w zależności od wymaganej dokładności, wolne bity uzupełniając zerami. Do reprezentacji liczb ze
znakiem stosuje siejże kod U2.
Np. Liczba 6,25=110,01(2) zapisana na 8 bitach gdy część ułamkowa zajmuje 3 najmłodsze bity, ma postać:
0
0
1
1
0
0
część całkowita
1
0
część ułamkowa
Natomiast liczba -6,25=-110,01(2) zapisana w powyższym formacie w kodzie U2, ma postać:
1
1
0
0
1
1
1
0
str. 7

Zapis zmiennopozycyjny.
Liczba zmiennoprzecinkowa jest komputerową reprezentacją liczb rzeczywistych zapisanych w postaci wykładniczej o
podstawie 2. Na zajęciach będziemy stosowali następującą notację:
z M 2C
S
gdzie:
z
M
C-S
C
S
-
znak liczby
znormalizowana mantysa (liczba ułamkowa spełniająca warunek: 1 M<2)
wykładnik (liczba całkowita)
spolaryzowana cecha (liczba całkowita umownie zwana cechą)
stała (liczba całkowita BIAS zależna od danej implementacji – rozwiązuje problem znaku wykładnika)
Uwaga:
 Powszechnie w procesorach i oprogramowaniu obliczeniowym wykorzystuje się binarny zapis
zmiennopozycyjnym zgodnym ze standardem IEEE754
(np. format 32-bitowy z polami: b31-znak, b23..30-cecha, b0..22-mantysa).
W przedstawieniu tym cecha, która jest ciągiem zer (albo ciągiem jedynek) nadaje kodowi specjalne
znaczenie, np.
01111111100000000000000000000000 +
00000000000000000000000000000000 0
Gdy cecha jest ciągiem zer mantysa jest zdenormalizowana tzn. 0,5 M<1
Ze względów dydaktycznych będziemy stosowali uproszczone formaty.
 Używając formatu zmiennopozycyjnego należy pamiętać o takich zagadnieniach jak: zakres (problem z
przepełnieniem i niedomiarem), zaokrąglanie, kolejność wykonywania działań (nie ma np. łączności)
 Liczbę, którą można dokładnie zapisać w danym formacie nazywamy liczbą maszynową.
Np.
Załóżmy, że operujemy następującym zmiennopozycyjnym formatem zapisu liczby rzeczywistej:
 na zapis przeznaczamy 16 bitów.
 najstarszy bit (b15) to bit znaku (będziemy stosować kod ZM),
 kolejne 6 bitów (b9-b14) to mantysa
 pozostałe bity (b0-b8) są przeznaczone na zapis cechy.
 przyjmijmy, że S=9.
Przedstawimy liczbę +0,0224609375 w powyższym formacie. Naszą liczbę zapisujemy w systemie binarnym w
postaci wykładniczej o podstawie 2:
0,0224609375 = 0,0000010111(2) = 1,0111(2) 2-6 = 1,0111(2) 23-9 = +1,0111(2) 211
-S
(2)
Oto liczba 0,0224609375 zapisana w zadanym formacie:
0
0
1
1
1
0
0
0
0
0
0
0
0
0
1
1
3.3. Kontrola transmisji danych

Bit parzystości

Suma kontrolna

CRC
http://wazniak.mimuw.edu.pl/index.php?title=MN03
str. 8
Zadania
z.3.1. Rozkoduj obraz:
a) 5X16 pikseli o głębi 1b/pix zakodowany kodem ASCII: &f UU Ue UW &U
z.3.2. Uzupełnij tabelkę (do zapisu liczb w kodzie ZM i U2 użyj minimalnej wielokrotności 8 bitów) :
(10)
1947
-1947
ZM
U2
01001110
11001110
01001101
11001101
z.3.3. Podaj zakres liczb całkowitych jakie można zapisać na 8 bitach:
a) w kodzie ZM
b) w kodzie U2
z.3.4. Uzasadnij, że liczba -1 w kodzie U2 jest reprezentowana zawsze jako ciąg jedynek.
z.3.5. Rozkoduj ciąg 10010001 zapisany w formacie stałopozycyjnym 8bitowym:
a) b0..5 – część całkowita, b6..7 – część ułamkowa (bez znaku)
b) b0..2 – część ułamkowa, b3..7 – część całkowita (bez znaku)
c) b0..2 – część ułamkowa, b3..6 – część całkowita, b7-znak (ZM)
d) b0..2 – część ułamkowa, b3..7 – część całkowita (U2)
z.3.6. Zapisz liczbę -112,09375 w 16bitowym formacie stałopozycyjnym:
a) b0..7 – część ułamkowa, b8..14 – część całkowita, b15-znak (ZM)
b) b0..7 – część ułamkowa, b8..15 – część całkowita (U2)
z.3.7. Podaj zakres i dokładność liczb jakie można zapisać w formacie stałopozycyjnym 8bitowym (bez znaku):
a) gdy część ułamkowa zajmuje 2 najmłodsze bity
b) gdy część ułamkowa zajmuje 5 najstarszych bitów
z.3.8. Zapisz w 16 bitowym formacie zmiennopozycyjnym: b15-znak, b14..7-znormalizowana mantysa, b6..0
spolaryzowana cecha przy S=20:
a) 9,1875
c) 503
b) 0,09375
d) -9,09375
z.3.9. Rozkoduj ciąg 10010001 zapisany w formacie zmiennopozycyjnym 8bitowym:
a) b7-znak, b6..3-znormalizowana mantysa, b0..2 spolaryzowana cecha przy S=8
b) b7-znak, b6..3-znormalizowana mantysa, b0..2 spolaryzowana cecha przy S=10
c) b0-znak, b7..4-znormalizowana mantysa, b1..3 spolaryzowana cecha przy S=10
d) b0-znak, b1..3-znormalizowana mantysa, b4..7 spolaryzowana cecha przy S=10
z.3.10. Podaj zakres jaki uzyskamy kodując liczby w formacie zmiennopozycyjnym 8 bitowym: b7-znak, b6..3znormalizowana mantysa, b0..2-spolaryzowana cecha przy S=8.
z.3.11. Wypisz i zaznacz na osi wszystkie liczby jakie można zakodować na 4 bitach w formacie zmiennopozycyjnym gdy
najstarszy bit jest bitem znaku, dwa następne bity są bitami spolaryzowanej cechy o stałej S=1, a najmłodszy bit jest
bitem znormalizowanej mantysy.
z.3.12. Określ, która z liczb jest liczbą maszynową, która z przepełnienia a która z niedomiaru gdy zapisane są w
formacie „zccmm” i są zapisane bez zastrzeżenia o cechach będących ciągiem jedynek i denormalizacji mantysy:
a) 2
c) -20
b) 0,2
d) -2,2
z.3.13. Dane słowa 8bitowe mają dodaną odpowiednią sumę kontrolną. Określ, które uległy zniekształceniu
a) 110111011
c) 01011101011
b) 0101110111
d) 0101110100
str. 9