Document

1. Kodowanie znak moduł:
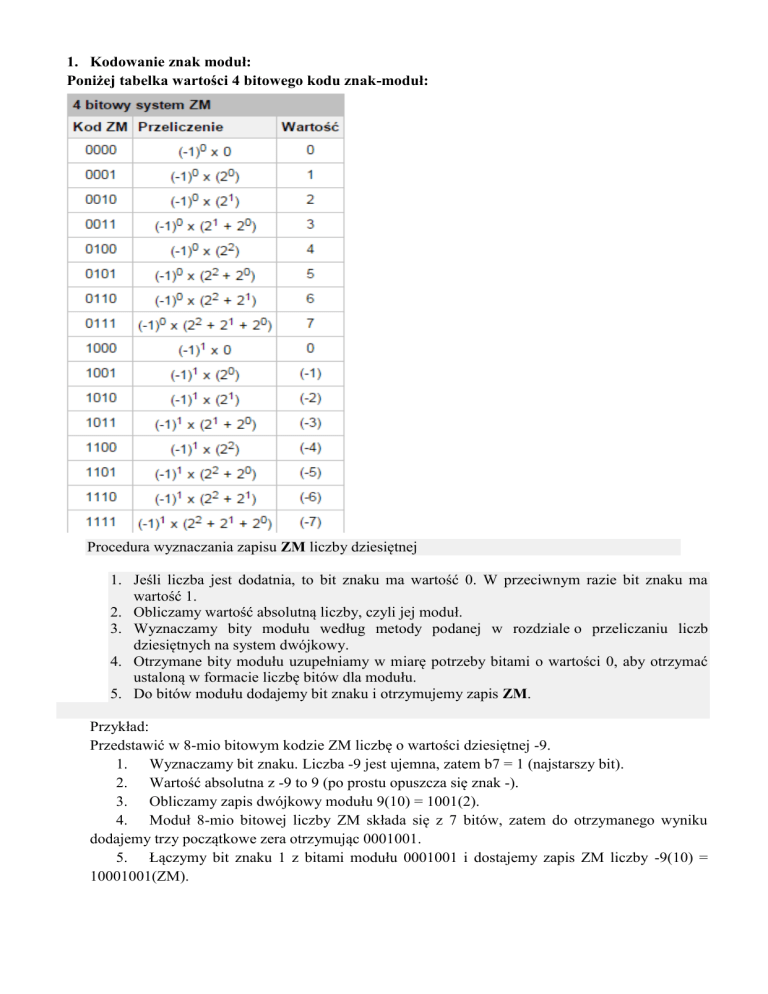
Poniżej tabelka wartości 4 bitowego kodu znak-moduł:
Procedura wyznaczania zapisu ZM liczby dziesiętnej
1. Jeśli liczba jest dodatnia, to bit znaku ma wartość 0. W przeciwnym razie bit znaku ma
wartość 1.
2. Obliczamy wartość absolutną liczby, czyli jej moduł.
3. Wyznaczamy bity modułu według metody podanej w rozdziale o przeliczaniu liczb
dziesiętnych na system dwójkowy.
4. Otrzymane bity modułu uzupełniamy w miarę potrzeby bitami o wartości 0, aby otrzymać
ustaloną w formacie liczbę bitów dla modułu.
5. Do bitów modułu dodajemy bit znaku i otrzymujemy zapis ZM.
Przykład:
Przedstawić w 8-mio bitowym kodzie ZM liczbę o wartości dziesiętnej -9.
1. Wyznaczamy bit znaku. Liczba -9 jest ujemna, zatem b7 = 1 (najstarszy bit).
2. Wartość absolutna z -9 to 9 (po prostu opuszcza się znak -).
3. Obliczamy zapis dwójkowy modułu 9(10) = 1001(2).
4. Moduł 8-mio bitowej liczby ZM składa się z 7 bitów, zatem do otrzymanego wyniku
dodajemy trzy początkowe zera otrzymując 0001001.
5. Łączymy bit znaku 1 z bitami modułu 0001001 i dostajemy zapis ZM liczby -9(10) =
10001001(ZM).
2. Przesunięcie bitowe w lewo:
Na najmłodszą pozycję dopisywany jest bit o wartości zero, natomiast najstarszy bit jest tracony, np.:
011010002 ----- 110100002 (10410---- 20810)
Wartość liczby w naturalnym kodzie binarnym jest 2 razy większa. Większe przesunięcia są
równoważne przemnożeniu przez potęgę dwójki.
3. Przesunięcie bitowe w prawo:
Na najstarszą pozycję dopisywany jest bit o wartości zero, natomiast najmłodszy bit jest tracony, np.:
100111012------ 010011102 (15710 -------7810)
Wartość liczby w naturalnym kodzie binarnym jest 2 razy mniejsza (dzielenie całkowitoliczbowe).
4. Przesuniecie arytmetyczne w prawo:
Używane dla liczb zapisanych w powszechnie stosowanym kodzie uzupełnień do dwóch (U2). Bit z
najstarszej pozycji jest powielany, natomiast najmłodszy bit jest tracony, np.:
10011100u2 ------- 11001110u2 (-10010 ------ -5010)
Gdyby zastosować zwykłe przesunięcie bitowe wynikiem byłoby 7810.
Zadania: Zapisz w kodzie ZM takie liczby:
a) -6
b) 11
c) -10
d) 2
e) 0
Zad 2 Dokonaj przesunięcia bitowego podanych liczb:
a) 01001110=.............................................
b) 01101001=..............................................
c) 00001111=................................................
d) 0111001=....................................................
Zad 3 Dokonaj przesunięcia arytmetycznego w prawo i w lewo liczb:
a) 10101010(u2)=.................................................................
b) 11100111(u2)=................................................................
c) 10011001(u2)=...............................................................
d) 10010011(u2)=...................................................................
e) 111010u2=........................................................................
f) 10101010u2=....................................................................