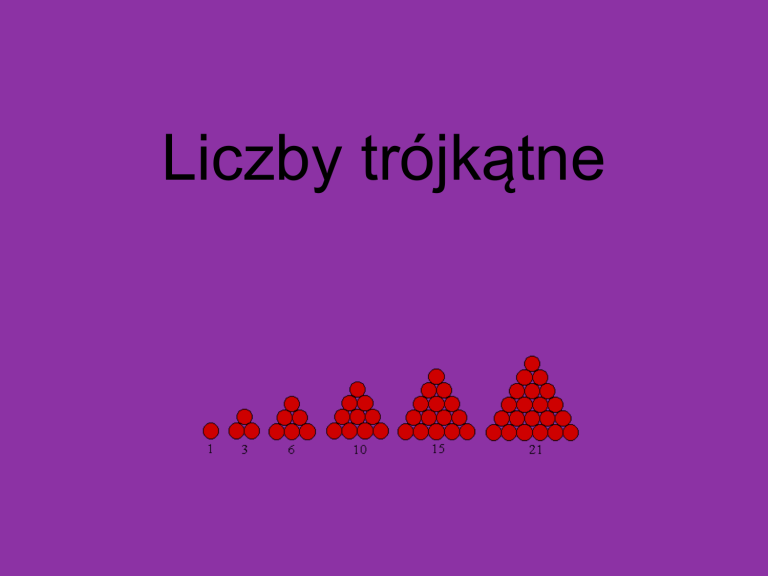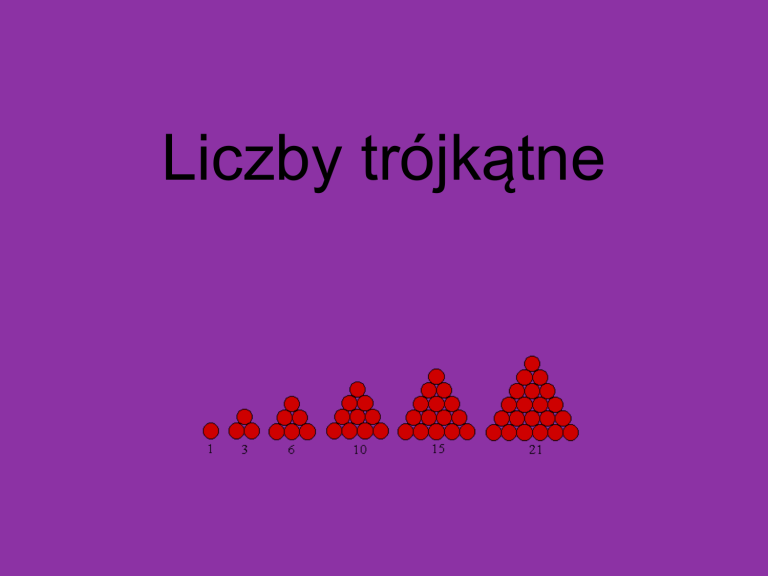
Liczby trójkątne
• Podczas budowania konstrukcji z klocków w kształcie piramidy,
trzeba pamiętać, by klocek z kolejnej warstwy leżał na dwóch
klockach z warstwy poprzedniej.
• Po ułożeniu podstawy musimy postawić na niej ścianę złożoną o
jeden klocek mniej. Zaczynając od podstawy z n klocków, w
następnej warstwie musimy ułożyć ich n - 1. Układamy tak długo, aż
na szczycie będzie tylko jeden klocek. Piramida skończona i
powstaje tylko pytanie: ilu klocków potrzeba było do jej zbudowania?
• Oznaczmy przez Tn liczbę klocków potrzebną do budowy piramidy
złożonej z n klocków. Łatwo możemy obliczyć tę liczbę, gdyż jest
ona zawsze sumą liczb naturalnych od 1 do n (dla n > 0). Liczbę tą
nazwano trójkątną.
• Liczba trójkątna jest sumą n kolejnych liczb naturalnych, która
wyraża się wzorem:
Tn = n ( n + 1 ):2
• Podobno wzór wymyślił młody Gauss, gdy nudził się na lekcji
matematyki. Liczby trójkątne są równe odpowiednim
współczynnikom newtonowskim.
Liczby trójkątne to liczby postaci:
tn=n(n+1):2
gdzie n jest liczbą naturalną.
Liczby trójkątne można także rozważać jako
liczbę kulek, z których można ułożyć trójkąt
równoboczny o podstawie n.
Każda liczba naturalna jest sumą co najwyżej
trzech liczb trójkątnych, na przykład:
4=3+1
5=3+1+1
6=6
W matematyce liczba trójkątna to liczba, którą można
przedstawić w postaci sumy kolejnych, początkowych
liczb naturalnych:
Tn = 1 + 2 + 3 + …+ (n - 1) + n
Kolejne liczby trójkątne to
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
Koniec