Ładunki elektryczne q = ne Zasada zachowania ładunku

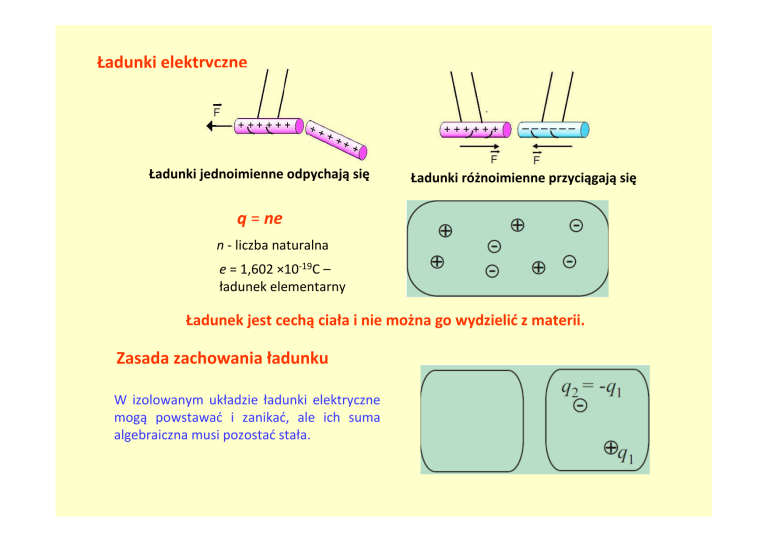
Ładunki elektryczne
Ładunki jednoimienne odpychają się
Ładunki różnoimienne przyciągają się
q = ne
n - liczba naturalna
e = 1,602 ×10-19C –
ładunek elementarny
Ładunek jest cechą ciała i nie można go wydzielić z materii.
Zasada zachowania ładunku
W izolowanym układzie ładunki elektryczne
mogą powstawać i zanikać, ale ich suma
algebraiczna musi pozostać stała.
Prawo Coulomba
Ładunki Q1 i Q2 równoimienne
Ładunki Q1 i Q2 równoimienne
Schemat doświadczenia
Coulomba
Prawo Coulomba zapis wektorowy
Natężenie pola elektrostatycznego
wektor natężenia pola w miejscu
umieszczenia ładunku próbnego q > 0
Pole elektrostatyczne ładunku punktowego
Pole elektrostatyczne układu ładunków
Linie pola elektrostatycznego - przykłady
Pole od nieskończonej płaszczyzny-
jednorodne pole elektrostatyczne
Strumień pola elektrycznego
Prawo Gaussa
Dla powierzchni zamkniętej
r
Wektor powierzchni S ; jego długość jest
równa polu powierzchni S, a jego kierunek
jest prostopadły do powierzchni
Prawo Gaussa dla ładunku punktowego
Jednorodne pole elektrostatyczne
E=
Pole pomiędzy naładowanymi płaszczyznami
σ
2εε 0
Pole elektryczne (elektrostatyczne):
- naładowanej powierzchni kulistej
- lub kuli metalowej
Pole kuli naładowanej objętościowo
Praca w polu elektrostatycznym
Energia potencjalna
w polu elektrostatycznym
Potencjał pola elektrostatycznego
Potencjał pola elektrostatycznego ładunku punktowego
Zasada superpozycji pól:
Zależność pomiędzy energią w polu sił zachowawczych a siłą - przypomnienie
dE p = − F ⋅ dx
E p = − ∫ F ⋅ dx
F =−
Związek między natężeniem pola a potencjałem
Przypadek jednowymiarowy:
Pole jednorodne (np. w kondensatorze):
dV
E=−
dx
E=−
U
d
dE p
dx
Dielektryk w jednorodnym polu elektrycznym
bez zewnętrznego pola elektrycznego
po umieszczeniu w polu elektrycznym: jedna powierzchnia ładuje się dodatnio a druga ujemnie
Pole elektryczne w dielektryku
Pole elektryczne w przewodniku
Przewodnik w zewnętrznym
polu elektrycznym
Ruch naładowanej cząstki
w polu elektrostatycznym
Siła działająca na ładunek q
w polu elektrostatycznym o
natężeniu wynosi:
q<0
q>0
+
E
F+
F-
-
E
r
E
r
r
F = qE
Siła ta jest zgodna z kierunkiem natężenia
pola dla q>0 i przeciwna dla q<0
Zgodnie z II zasadą dynamiki siła ta powoduje przyspieszenie cząstki
r
r
r F qE
a= =
m m
Zasada zachowania energii w polu elektrostatycznym
Cząstka o ładunku q>0 porusza się
w polu elektrostatycznym
v2
+
Jaka jest różnica, gdy cząstkę
dodatnią zamienimy na ujemną?
V2
v1
q>0
V1
Stąd zmiana energii kinetycznej
Całkowita energia E cząstki, czyli suma energii
kinetycznej i potencjalnej jest zachowana, czyli
taka sama w punkcie 1 i 2
mv12
mv22
+ qV1 =
+ qV2
2
2
cząstki wynosi:
mv22 mv12
−
= qV1 − qV2 = qU ,
2
2
Zadanie. Cząstka o masie m naładowana dodatnim
ładunkiem q porusza się, bez prędkości początkowej od
okładki dodatniej do ujemnej. Odległość między okładkami
kondensatora wynosi d a kondensator naładowany jest do
napięcia U. Jaką końcową prędkość uzyska ta cząstka?
F
+
+
+
d
qU
F = qE =
d
Stąd prędkość końcowa wynosi
vk = at ⇒ vk = a
−
−
E
+
F
a=
m
gdzie
a siła równa jest
+
+
I sposób rozwiązania:
at 2
d=
2
−
+
−
−
−
2d
2qU
= 2da =
a
m
II sposób rozwiązania:
Początkowo energia kinetyczna cząstki jest równa zeru natomiast energia potencjalna, jeżeli
przyjmiemy zero energii potencjalnej przy okładce ujemnej, wynosi qU, gdzie U- napięcie na
okładkach. Podczas ruchu elektronu rośnie energia kinetyczna kosztem energii potencjalnej.
Stąd:
mvk2
qU + 0 =
+0
2
a stąd
vk =
2qU
m