Zjawisko piezoelektryczne

Grawitacja
Wykład 7
Wrocław University of Technology
1
Grawitacja
Droga mleczna
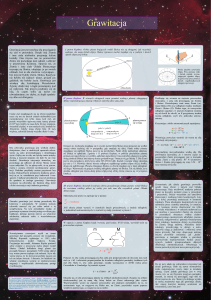
Droga Mleczna – galaktyka spiralna z poprzeczką, w której znajduje się m.in. nasz Układ
Słoneczny. Galaktyka zawiera od 100 do 400 miliardów gwiazd. Ma średnicę około
100000 lat świetlnych i grubość ok. 12 000 lat świetlnych.
2
Grawitacja
Układ Słoneczny
Układ Słoneczny – układ planetarny składający się ze Słońca i powiązanych z nim
grawitacyjnie ciał niebieskich. Ciała te to osiem planet, ponad 160 znanych księżyców,
pięć znanych (a prawdopodobnie kilkadziesiąt) planet karłowatych i miliardy (a być może
nawet biliony) małych ciał Układu Słonecznego, do których zalicza
się planetoidy, komety, meteoroidy i pył międzyplanetarny.
3
Grawitacja
Układ Słoneczny
Gwiazda – kuliste ciało niebieskie stanowiące skupisko powiązanej grawitacyjnie materii w
stanie plazmy. Przynajmniej przez część swojego życia gwiazda w sposób
stabilny emituje powstającą w jej jądrze w wyniku procesów syntezy jądrowej atomów
wodoru energię w postaci promieniowania elektromagnetycznego, w
szczególności światło widzialne.
4
Grawitacja
Układ Słoneczny
Rok świetlny (ang. light year) – jednostka odległości stosowana w astronomii. Jest
równy odległości, jaką pokonuje światło w próżni w ciągu jednego roku
kalendarzowego.
W przeliczeniu na inne jednostki:
1 rok świetlny = 0.3066 pc = 63241 j.a. = 9.4607·1015 m
W szacunkowych obliczeniach przyjmowana jest zazwyczaj wartość przybliżona ≈
9,5 biliardów m (9,5 bilionów km).
•
Odległość od Ziemi do Księżyca światło pokonuje w ok. 1,3 s, co powodowało
opóźnienia w komunikacji podczas misji załogowych Apollo.
• Około 8 minut i 20 sekund zajmuje światłu podróż ze Słońca do Ziemi.
• Najbliższa znana gwiazda, Proxima Centauri jest położona w odległości 4,22 lat
świetlnych od Słońca.
• Średnica Drogi Mlecznej wynosi w przybliżeniu 100 000 lat świetlnych.
5
Grawitacja
Prawo powszechnego ciążenia
Newton stwierdził, że nie tylko Ziemia przyciąga jabłko i Księżyc, lecz każde ciało
we Wszechświecie przyciąga każde inne. Tę skłonność ciał do zbliżania się do
siebie nazwał ciążeniem (grawitacją).
Przyciąganie ciał opisuje ilościowo prawo wprowadzone przez Newtona nazywane
prawem powszechnego ciążenia, które mówi, że każda cząstka przyciąga każdą
inną cząstkę siłą ciężkości (siłą grawitacyjną) o wartości:
m2

F
m1m2
F G 2
r
gdzie G – stała grawitacji 6.67 . 10-11 Nm2kg-2.
m1

F
r
6
Grawitacja
Prawo powszechnego ciążenia
Ciało w kształcie jednorodnej powłoki kulistej przyciąga cząstkę znajdującą się na
zewnątrz powłoki tak, jak gdyby cała masa powłoki była skupiona w jej środku.
7
Grawitacja
Zasada superpozycji
Dla n oddziałujących ze sobą cząstek zasada superpozycji dla sił grawitacyjnych ma
postać:





F1wyp  F12  F13  F14  ...  F1n
n 

F1wyp   F1i
i 1
W przypadku granicznym dzielimy ciało rozciągłe na nieskończenie małe
elementy masy dm, z których każdy działa na cząstkę siłą dF. Suma
przechodzi wtedy w całkę


F1   dF
8
Grawitacja
Grawitacja w pobliżu Ziemi
Załóżmy, że Ziemia jest jednorodną kulą o masie M, wtedy
Mm
F G 2
r
Z drugiej zasady dynamiki Newtona wiemy, że
F  mag
Stąd
GM
ag  2
r
Wysokość [km]
ag [m/s2]
0
8.8
36.6
400
35700
9.83
9.80
9.71
8.70
0.225
(powierzchnia Ziemi)
(szczyt Mt. Everestu)
(największa wysokość załogowego lotu balonem)
(wahadłowiec kosmiczny na orbicie)
(satelita telekomunikacyjny)
9
Grawitacja
Grawitacja w pobliżu Ziemi
Przyczyny różnej wartości ag:
• Ziemia nie jest jednorodna. Gęstość Ziemi (tzn. masa jej jednostkowej
objętości) zmienia się wzdłuż jej promienia, a do tego gęstość skorupy
ziemskiej (czyli jej najbardziej zewnętrznej części) jest różna w różnych
miejscach na powierzchni Ziemi. Wobec tego w różnych miejscach na
powierzchni Ziemi wartość g jest nieco inna.
10
Grawitacja
Grawitacja w pobliżu Ziemi
• Ziemia nie jest kulista. Ziemia ma w przybliżeniu kształt elipsoidy obrotowej,
spłaszczonej przy biegunach, a grubszej w okolicy równika. Promień Ziemi na
równiku jest o 21 km większy od jej promienia na biegunie. Gdy ciało znajduje się
na biegunie, jest ono zatem bliżej gęstego jądra Ziemi niż wtedy, gdy znajduje się na
równiku. Jest to jeden z powodów, dla którego przyspieszenie swobodnego spadku
ciała rośnie w miarę przemieszczania go - na poziomie morza - z równika na biegun.
11
Grawitacja
Grawitacja w pobliżu Ziemi
• Ziemia obraca się. Oś obrotu Ziemi przechodzi przez jej bieguny: północny i
południowy. Ciało umieszczone na powierzchni Ziemi gdziekolwiek poza
biegunami wykonuje zatem ruch po okręgu wokół tej osi, przy czym ma ono
przyspieszenie dośrodkowe skierowane do środka tego okręgu. Źródłem tego
przyspieszenia musi być siła dośrodkowa, skierowana także do tego środka okręgu.


 m R 
N  mag  m   2 R
mg  mag
zmierzony ciężar = wartość siły ciężkości
2
_
masa x przyspieszenie dośrodkowe
g  ag   2 R
Przyspieszenie
spadku ciała
=
Przyspieszenie
grawitacyjne
_
Przyspieszenie
dośrodkowe
12
Grawitacja
Grawitacyjna energia potencjalna
Grawitacyjna energia potencjalna wyraża się wzorem:
GMm
Ep  
r
Gdy badany układ składa się z więcej niż dwóch cząstek, rozważamy każdą parę
cząstek po kolei, obliczając grawitacyjną energię potencjalną tej pary, jak gdyby
innych cząstek nie było, po czym dodajemy do siebie otrzymane wyniki. Na
przykład dla układu trzech cząstek, wyznaczając energię potencjalną każdej ich
pary, otrzymujemy energię potencjalną układu równą
 Gm1m2 Gm2 m3 Gm3m1 

E p  


r23
r31 
 r12
13
Grawitacja
Prędkość ucieczki
Ciało ma się zatrzymać w nieskończoności, a zatem ma tam mieć energię
kinetyczną równą zeru. Jego energia potencjalna będzie wówczas także równa
zeru, gdyż tak właśnie wybraliśmy konfigurację ciał odpowiadającą zerowej energii
potencjalnej. Całkowita energia pocisku jest zatem w nieskończoności równa
zeru. Z zasady zachowania energii wynika, że jej całkowita energia musi być
równa zeru także na powierzchni planety, wobec czego
2
GMm
mv


E p  Ek   
0

R 
2


2GM
v
R
14
Grawitacja
Prędkość ucieczki
Ciało
Masa
[kg]
Promień
[m]
1.17.1021
3.80.105
0.64
KSIĘŻYC ZIEMI
7.36.1022
1.74.106
2.38
ZIEMIA
5.98.1024
6.37.106
11.2
JOWISZ
1.90.1027
7.15.107
59.5
SŁOŃCE
1.99.1030
6.96.108
618
SYRIUSZ B
2.00.1030
1.00.107
5200
2.00.1030
1.00.104
2.105
CERES
Prędkość
ucieczki [km/s]
(najcięższa planetoida)
(biały karzeł)
GWIAZDA
NEUTRONOWA
15
Grawitacja
Prawa Keplera
Pierwsze prawo Keplera:
Wszystkie planety poruszają się po orbitach w kształcie elipsy w której ognisku
znajduje się Słońce.
Wielkość orbity jest wyznaczona przez wartość jej półosi wielkiej a i mimośrodu e,
zdefiniowanego tak, że ea jest odległością każdego z ognisk elipsy F i F' od jej
środka. Mimośród równy zeru odpowiada okręgowi, będącemu przypadkiem
16
szczególnym elipsy, w którym oba ogniska są jednym punktem.
Grawitacja
Prawa Keplera
Drugie prawo Keplera:
Linia łącząca planetę ze Słońcem zakreśla w jednakowych odstępach czasu
jednakowe pola powierzchni w płaszczyźnie orbity; inaczej mówiąc, wielkość
dS/dt, przy czym S jest polem powierzchni zakreślonej przez tę linię, jest stała.
Z prawa tego wynika, że planeta porusza się wolniej, gdy jest daleko od Słońca, a
szybciej, gdy jest bliżej niego. II prawo Keplera mówi, że w ruchu planet
17
spełniona jest zasada zachowania momentu pędu
Grawitacja
Prawa Keplera
Drugie prawo Keplera:
Pole powierzchni tego klina ΔS jest równe w przybliżeniu polu trójkąta o podstawie rδθ
i wysokości r. Chwilowa szybkość zmiany pola powierzchni jest wobec tego równa
dS 1 2 d 1 2
 r
 r
dt 2 dt 2
L  rp  r mv   r mr   mr 2
dS
L

dt 2m
18
Grawitacja
Prawa Keplera
Trzecie prawo Keplera:
Kwadrat okresu ruchu każdej planety na orbicie wokół Słońca jest proporcjonalny do
sześcianu półosi wielkiej tej orbity.
T 2 4 2

3
r
GM
Planeta
Mercury
Wenus
Ziemia
Mars
Jowisz
Saturn
Uran
Neptun
Pluton
Półoś wielka a
[1010 m]
5.79
10.8
15.0
22.8
77.8
143.0
287.0
450.0
590.0
Okres T
[a]
0.241
0.615
1.00
1.88
11.9
29.5
84.0
165.0
248.0
T2/a3
[10-34 a2/m3]
2.99
3.00
2.96
2.98
3.01
2.98
2.98
2.99
2.99
19
Grawitacja
Przykłady
Załóżmy, że prędkość ucieczki z planety jest tylko nieznacznie większa
niż prędkość ucieczki z Ziemi, ale planeta jest znacznie większa od Ziemi. Jaka
będzie (średnia) gęstość planety w porównaniu do (średniej) gęstości Ziemi?
Gęstości planet są związane z prędkością ucieczki z ich powierzchni przez:
vZiemi
2GM Ziemi

RZiemi
v planety 
2GM planety
R planety
Wyrażając stosunek prędkości ucieczki z planety do prędkości ucieczki z Ziemi i
upraszczając:
2GM planety
v planety
vZiemi

R planety
2GM Ziemi
RZiemi

RZiemi M planety
R planety M Ziemi
20
Grawitacja
Przykłady
Ponieważ
vZiemi  v planety  1 
RZiemi M planety
RZiemi M planety
 1
R planety M Ziemi
R planety M Ziemi
Wyrażając Mplanety i MZiemi przez ich gęstości i upraszczając:
3
2
4


R

V

R
p
p
R
R
p p
p p
3
1 Z
 Z

R p  ZVZ R p  Z 4 RZ3  Z RZ2
3

 p RZ2
 2
Z Rp
Ponieważ planeta jest znacznie większa niż Ziemia, stąd
p
 1
Z
Wniosek: Gęstość planety musi być mniejsza niż gęstość Ziemi!
21
Grawitacja
Przykłady
Oszacuj masę naszej Galaktyki (Drogi Mlecznej) jeśli Słońce obiega centrum
Galaktyki z okresem 250 milionów lat, średniej odległości 30.000 lat
świetlnych. Wyrazić masę w postaci wielokrotności masy Słońca MS.
Do oszacowania masy galaktyki załóżmy, że centrum galaktyki to punkt masy, z
krążącym wokół niej po orbicie Słońcem i zastosujmy trzecie prawo
Keplera. Niech MG reprezentuje masę galaktyki
2
4

T2 
Ro3
GM G

MG
4 2 R03

M S GM S T 2
Podstawiając wartości liczbowe otrzymujemy:
3
15

9
.
461

10
m
2
4

4  3.00 10 l. y. 
l. y.
MG




2

11
2

2
30
6
7

1
M S 6.6742 10 Nm kg 1.99 10 kg 250 10 y  3.156 10 sy 
 1.11011
M G  1.11011 M S
22
Grawitacja
Przykłady
Masa Saturna wynosi 5.69 × 1026 kg.
(a) Znaleźć okres jego księżyca Mimas, który porusza się po orbicie o promieniu
1.86×108 m.
(b) Znaleźć średni promień orbity księżyca Titan, którego okres wynosi 1.38×106 s.
a) Skorzystamy z trzeciego prawa Keplera:
2
4

TM2 
rM3
GM S
4 2 3
TM 
rM
GM S

Podstawiając wartości liczbowe, otrzymujemy:
TM 


4 1.86 10 m
4

8
.
18

10
s  22.7h
11
2
2
26
6.6726 10 Nm kg 5.69 10 kg
2

8

3

23
Grawitacja
Przykłady
(b) Znaleźć średni promień orbity księżyca Titan, którego okres wynosi 1.38×106 s.
b) Podobnie jak w punkcie a) skorzystamy z trzeciego prawa Keplera:
2
4

TT2 
rT3
GM S
TT2GM S
rT 
4 2

Podstawiając wartości liczbowe, otrzymujemy:
rT 
1.38 10 s  6.6726 10
6
3
2
11

Nm 2 kg  2 5.69 10 26 kg
4 2

 1.22 109 m
24
Grawitacja
Przykłady
Promień Ziemi jest 6370 km, a promień księżyca 1738 km. Przyspieszenie
grawitacyjne na powierzchni Księżyca wynosi 1.62 m/s2. Jaki jest
stosunek średniej gęstości Księżyca do Ziemi?
Wyraźmy przyspieszenie ziemskie na powierzchni Ziemi przez średnią gęstość Ziemi:
4 R 3
G

Z
Z
GM Z G ZVZ
3
gZ 


2
2
RZ
RZ
RZ2
Przyspieszenie grawitacyjne na księżycu
4
g K  G K RK
3
Dzieląc oba równania przez siebie otrzymujemy:
g K  K RK

gZ
 Z RZ
 K g K RZ


 0.65
 Z g Z RK
25
Grawitacja
Przykłady
Cztery identyczne planety są ułożone w kwadrat, jak pokazano na rysunku. Jeżeli
masa każdej planety wynosi M i długość kwadratu a, jakie są ich prędkości, jeżeli
krążą po orbicie względem wspólnego środka pod wpływem ich wzajemnego
przyciągania?
26
Grawitacja
Przykłady
Wyraźmy przyspieszenie ziemskie na powierzchni Ziemi przez średnią gęstość Ziemi:


 Frad  marad
Fc  2F1 cos   F2
Podstawiając za F1, F2 oraz θ i upraszczając:
2GM 2
GM 2
2GM 2 1 GM 2 GM 2 
1
FC 
cos 45 



 2 
2
2
2
2
2
a
a
2a
a 
2
2
a 2


Ponieważ
Mv 2
FC 

a/ 2
2Mv 2
a

2Mv 2 GM 2 
1

 2 
2
a
a 
2
Rozwiązując dalej:
GM 
1 
GM
v
1 
  1.16
a  2 2
a
27