Pomiary dużych prądów

7. Pomiary dużych prądów o f = 50Hz
1. Wstęp
Pomiary prądów przemiennych o częstotliwości 50 Hz i wartościach od kilkudziesięciu do
kilku tysięcy amperów są możliwe za pomocą przetworników pomiarowych. W sieciach
elektroenergetycznych najczęściej stosowane są przekładniki prądowe, rzadziej boczniki
prądowe, a to ze względu na ich nieprzydatność przy wysokim napięciu. Do jednorazowych
pomiarów dużych prądów o niskim napięciu (U600V) wygodnym przyrządem jest tzw.
amperomierz cęgowy.
Stosunkowo nowym przetwornikiem pomiarowym, mogącym znaleźć powszechne
zastosowanie w pomiarach dużych prądów jest czujnik indukcyjny, w którym w
przeciwieństwie do przekładnika prądowego istnieje ,,słabe” sprzężenie magnetyczne między
obwodem z mierzonym prądem a obwodem wtórnym.
2. Pomiar dużych prądów za pomocą przekładnika prądowego
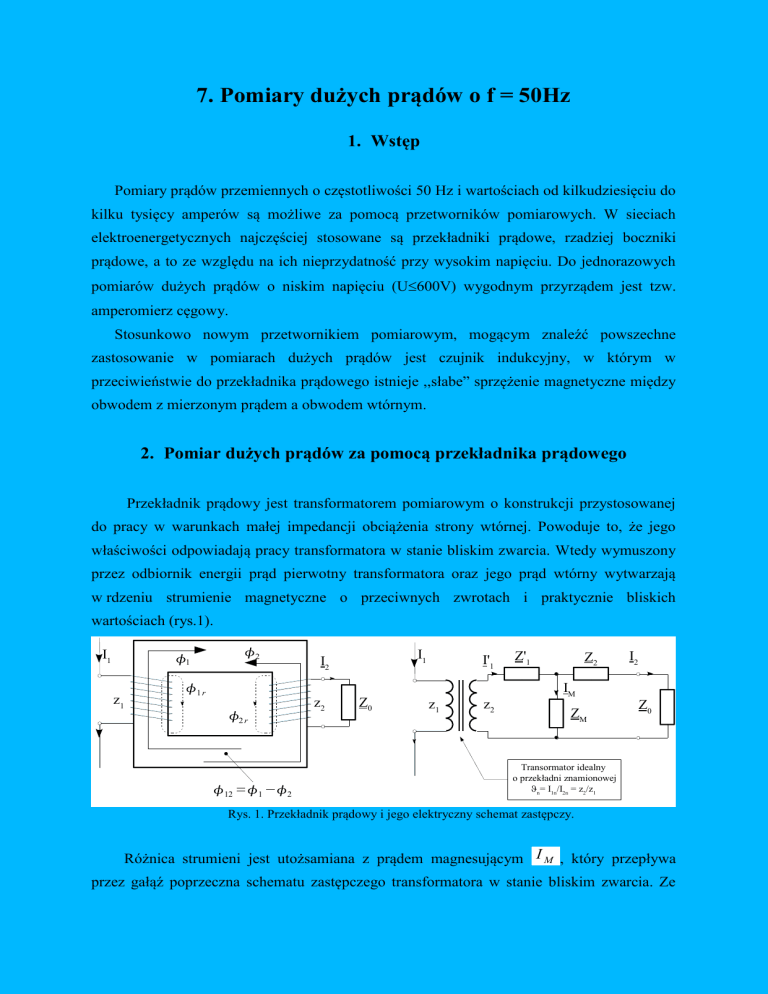
Przekładnik prądowy jest transformatorem pomiarowym o konstrukcji przystosowanej
do pracy w warunkach małej impedancji obciążenia strony wtórnej. Powoduje to, że jego
właściwości odpowiadają pracy transformatora w stanie bliskim zwarcia. Wtedy wymuszony
przez odbiornik energii prąd pierwotny transformatora oraz jego prąd wtórny wytwarzają
w rdzeniu strumienie magnetyczne o przeciwnych zwrotach i praktycznie bliskich
wartościach (rys.1).
I1
2
1
z1
I1
I2
I'1
2r
12
1
2
Z0
Z2
I2
IM
1r
z2
Z'1
z1
z2
ZM
Z0
Transormator idealny
o przekładni znamionowej
n= I1n/I2n = z2/z1
Rys. 1. Przekładnik prądowy i jego elektryczny schemat zastępczy.
Różnica strumieni jest utożsamiana z prądem magnesującym I M , który przepływa
przez gałąź poprzeczna schematu zastępczego transformatora w stanie bliskim zwarcia. Ze
schematu zastępczego wynika też to, że prąd magnesujący jest równy
różnicy prądów I2 i I'1 , którą można zdefiniować zespolony błąd
przetwarzania przekładnika:
IM
I'1
δI =
I 2  I `1
I
= M
I `1
I `1
(1)
W praktyce, do opisu dokładności przekładnika wykorzystuje się dwa
błędy. Są to:
I2
- błąd prądowy:
δ1 =
I2

w którym: n =
I 1n
I 2n
n
 I1
I1
,
- jest przekładnią znamionową przekładnika,
I 1n , I 2 n - prądami znamionowymi przekładnika,
- błąd kątowy , przyjmowany za dodatni gdy I 2 wyprzedza prąd I 1
(rys. 2).
Oba błędy mogą być zdefiniowane za pomocą składowej czynnej i biernej prądu
Rys. 2. Wykres
wektorowy prądów
magnesującego IM (patrz wykres).
O dokładności przekładnika w pomiarach prądu decyduje tylko błąd przekładni,
zaś w pomiarach mocy i energii analiza metrologiczna musi uwzględniać oba błędy. Wartości
obu błędów są funkcją prądu I 1 oraz obciążenia Z 0 . Ze względu na ważność pomiarów
wykonywanych za pomocą przekładników, ich właściwości oraz warunki stosowania
podlegają ścisłym normom (np. podział na klasy dokładności).
Do
pomiaru
prądu
wtórnego
przekładnika
stosuje
się
głównie
mierniki
elektromagnetyczne, których wskazania nie zależą od kształtu przebiegu czasowego prądu.
Mierzą one wartości skuteczne, a więc przydatne są do pomiarów prądów odkształconych 50
Hz.
3. Pomiar dużych prądów z zastosowaniem bocznika prądowego
Bocznik jest rezystorem wzorcowym, który włączony w obwód prądowy wytwarza napięcie proporcjonalne do wartości przepływającego prądu. Boczniki wykonywane są na
maksymalne prądy do kilku tysięcy amperów (np. firma LUMEL produkuje bocznik na prądy
do 4kA). Rezystancje boczników są małe i wynoszą od 10-4 do 10-1. Ich poważną wadą
jest powstająca w nich duża moc, równa np. I2R=(1000A)210-4=100W. Stąd konstrukcja
boczników powinna umożliwiać skuteczny odpływ wydzielającego się w nich ciepła.
2
Boczniki wykonywane są w klasach dokładności 0,05; 0,1; 0,2 i znamionowych spadkach
napięcia: 60; 100; 150mV.
Do pomiarów występujących na bocznikach spadków napięć mogą być stosowane
dowolne mierniki prądu przemiennego, jednakże o pomijalnie małym poborze mocy.
Gwarantują to mierniki analogowe i cyfrowe, wyposażone we wzmacniacze pomiarowe o
bardzo dużej impedancji wejściowej.
Jeżeli napięcie mierzone ma przebieg odkształcony (niesinusoidalny), woltomierz
zastosowany do jego pomiaru powinien mieć przetwornik wartości skutecznej (TRUE RMS).
Gdy miernik ma przetwornik wartości średniej bądź szczytowej, wówczas należy się liczyć
z dużymi błędami dodatkowymi.
4. Pomiar dużych prądów za pomocą amperomierza cęgowego
Amperomierze cęgowe umożliwiają pomiary dużych prądów (do 1000 A) bez
konieczności
przerywania obwodu z mierzonym prądem. Na przewód czy też szynę z
prądem, który w tym przypadku stanowi uzwojenie pierwotne transformatora, nakłada się
,,cęgi” w postaci rozwieranego rdzenia ferromagnetycznego. Na rdzeniu znajduje się
uzwojenie wtórne zwykle zawierające odczepy służące do zmiany zakresu pomiarowego.
Napięcie indukowane w uzwojeniu wtórnym jest w szerokich granicach proporcjonalne
do mierzonego prądu. Do jego pomiaru stosuje się miernik magnetoelektrycznym z
prostownikiem bądź woltomierz cyfrowy. Niektóre amperomierze cęgowe z odczytem
cyfrowym mogą być stosowane do pomiarów prądów odkształconych. Klasy dokładności
mierników analogowych wynoszą 1,5 lub 2,5. Amperomierze cęgowe z odczytem cyfrowym
są dokładniejsze, bo np. miernik firmy LUMEL ma dokładność 0,5%Ix  10cyfr.
Są też amperomierze cęgowe wyposażone w mikroprocesor. Wykorzystanie cyfrowego
przetwarzania sygnału umożliwia, po pierwsze - wykonać dokładne pomiary wartości
skutecznej prądów o znacznym odkształceniu, po drugie – wyznaczyć inne parametry
mierzonego prądu, włącznie z analizą zawartości harmonicznych.
3
5. Pomiar dużych prądów za pomocą czujnika indukcyjnego
W czujniku indukcyjnym wykorzystuje się do przetwarzania mierzonego prądu na
napięcie zjawisko indukcji elektromagnetycznej zachodzące pomiędzy dwoma obwodami
elektrycznymi ze ,,słabym” sprzężeniem magnetycznym, tzn. sprzężeniem poprzez
środowisko nieferromagnetyczne. Wynikiem tego, energia pola magnetycznego wiążąca oba
obwody jest bardzo mała, niewielkie jest także napięcie indukujące się w uzwojeniu wtórnym
czujnika.
W praktyce uzwojenie wtórne czujnika nawinięte jest na pierścień (toroid) wykonany
z aluminium. Uzwojenie pierwotne stanowi przewód z mierzonym prądem przechodzący
przez środek pierścienia (rys.3).
Tu strumienie
się dodają
e
Ix
M
di x
dt
Bzew
x
Tu strumienie
się odejmują
Rys. 3. Wpływ pola zewnętrznego na czujnik indukcyjny.
Staranne wykonanie konstrukcji czujnika, polegające na zachowaniu stałego przekroju
poprzecznego rdzenia oraz na równomiernym rozłożeniu uzwojenia wzdłuż obwodu,
powoduje jego dużą nieczułość na zewnętrzne pola elektromagnetyczne, i to pomimo małego
pola magnetycznego w rdzeniu. Jest to wynikiem kompensacji skutków oddziaływań pola
zewnętrznego, co zobrazowano na rys. 3. Na właściwości czujnika nie wpływa też brak
koncentrycznego położenie rdzenia względem przewodu z mierzonym prądem.
IMAX
ix(t)
0
e(t)
-IMAX
0
T/4
T/2
3
/4T
T
5
/4 T
3
7
/2 T
/4 T
2T
czas
Rys. 4. Przebieg czasowy prądu Ix i odpowiadający mu przebieg napięcia E indukowanego w czujniku.
Sygnałem wyjściowym czujnika indukcyjnego jest napięcie e(t), którego przebieg
czasowy jest określony pochodną przebiegu mierzonego prądu (rys. 4). Przetworzenie
napięcia e(t), polegające na jego prostowaniu i uśrednieniu, prowadzi do uzyskania sygnału
proporcjonalnego do wartości maksymalnej prądu ix(t). Uzasadnienie tego wynika z
następujących związków: wartość średnia napięcia wyprostowanego jest równa
T /2
1
2
E=
et  dt =

T /2 0
T
W
sieciach
T /2

0
di
2
 M x dt = M
dt
T
elektroenergetycznych
T /2
T /2
2
2
| =



di
=

Mi
M ix T / 2  ix 0 
x
x

0
T
0
przebiegi
czasowe
T
prądów
.
spełniają
warunek
nieparzystości, czyli ix(t)= -ix(t+T/2). Wtedy
E=
4
Mi x 0 .
T
Z przyjętego na wstępie warunku całkowania w granicach półokresu przebiegu e(t) wynika,
że dla wartości e1(0) = 0 jest i(0) = Imax , i stąd
E=
4
MI max = 4 f M I max
T
(2)
Ostatnia zależność dowodzi możliwości wyznaczania wartości maksymalnej prądu Ix z
pomiaru wartości średniej napięcia wyjściowego czujnika i to niezależnie od kształtu
przebiegu czasowego prądu. Zatem odpowiednimi miernikami do pomiaru napięcia czujnika
są woltomierze zawierające przetworniki wartości średniej. Jednak woltomierze te są
wzorcowane w wartościach skutecznych napięć sinusoidalnych, czyli istnieje konieczność
korekcji ich wskazań o współczynnik wiążący wartości skuteczną i średnią przebiegu
sinusoidalnego:
E=
π
2 2
(3)
E = 1 .11 E
Po uwzględnieniu zależności (3) we wzorze (2), wartość maksymalną mierzonego prądu
przedstawia wzór
I max =
E
4 .44 f M
(4)
Ostatecznie wartość skuteczną prądu sinusoidalnego można wyznaczyć z zależności:
I=
I max
E
=
2π f M
2
(5)
Uwaga! Zależność (5) jest słuszna tylko dla prądu sinusoidalnego. Do obliczania wartości
skutecznej przebiegu odkształconego stosowanie zależności (5) nie ma metrologicznego
uzasadnienia.
Pomiar wartości chwilowych prądu Ix
Całkowanie przebiegu chwilowego napięcia e(t) w przedziale całkowania równym
półokresowi mierzonego prądu, czyli w przedziale (t1,...,t1-T/2) - gdzie t1 jest początkowym
momentem całkowania, daje sygnał proporcjonalny do wartości chwilowej przebiegu prądu
ix(t1), czyli wartości prądu w chwili t1.
Jeżeli
stosowany przetwornik
całkujący będzie miał
możliwość zmiany
początkowego momentu całkowania, to kolejno uzyskane na jego wyjściu sygnały pozwolą
odtworzyć przebieg czasowy mierzonego prądu. Uzasadnienie tego wynika z poniższych
związków:
ti + T / 2

ti + T / 2
et  dt =  M
 dix = M ix ti +T / 2  ix ti ,
ti
ti
Ponieważ
ti + T / 2
ix(ti + T/2) = -ix(ti), to
 et dt = 2 M ix ti 
ti
Ostatecznie
ix ti  =
ti + T / 2
 et  dt
ti
2M
Z prawa indukcji w postaci e =
dψ
wynika, że wartość całki z napięcia e(t) określa
dt
zmianę strumienia magnetycznego. W związku z tym, wartość prądu chwilowego oblicza się
z zależności
ΔΦti , ti + T / 2
2M
ix ti  =
(6)
Mierniki realizujące operacje całkowania napięcia czujnika indukcyjnego zwane są
strumieniomierzami bądź weberomierzami.
Z uzyskanych wartości chwilowych przebiegu prądu można wyznaczyć jego wartość
skuteczną, wykorzystując do tego definicję wartości skutecznej dla sygnałów dyskretnych
Ix =
1
N
N
 i t 
2
x
(7)
i
i=1
w której: N - liczba próbek uzyskanych w jednym okresie przebiegu prądu; ix(ti) - wartość itej próbki (i = 1, ...,N).
Do
przeprowadzenia
obliczeń
wartości
skutecznej
wymagany
jest
układ
mikroprocesorowy. Elementy te są obecnie powszechnie stosowane w aparaturze pomiarowej,
więc zastosowanie ich w miernikach z czujnikiem indukcyjnym nie stwarza większych
problemów.
6. Program ćwiczeń
Celem pomiarów jest opracowanie wniosków dotyczących oceny dokładności
i przydatności poszczególnych metod pomiarowych do pomiaru dużych wartości prądów.
Program ćwiczenia obejmuje:
1. Pomiary wartości skutecznych prądów o przebiegu sinusoidalnym:
a)
za pomocą przekładnika prądowego,
b)
przez pomiar spadku napięcia na oboczniku,
c)
za pomocą przetwornika indukcyjnego,
d)
amperomierzem cęgowym.
Otrzymane wyniki i obliczenia zestawić w Tab.1.
2. Pomiary wartości skutecznych prądów niesinusoidalnych przyrządami i metodami jak
w punkcie 1.
Otrzymane wyniki i obliczenia zestawić Tab. 2.
3. Za pomocą strumieniomierza wyznaczyć wartości chwilowe prądu o przebiegu
odkształconym i na ich podstawie obliczyć wartość skuteczną prądu.
Wyniki zestawić w Tab. 3. Wykreślić przebieg ix(t1).
Układ pomiarowy przedstawia rysunek 5. W obwodzie występuje dławik D
powodujący po jego włączeniu znaczne zniekształcenie przebiegu prądu. Przy wyłączonym
dławiku mierzony prąd można przyjąć za sinusoidalnie zmienny. Włączenie i wyłączanie
dławika
można
dokonać
w
stanie
bezprądowym.
Do
nastawiania
prądu
służy
autotransformator AT.
D
AT
T
230V
50Hz
AC
P
RN
K
M
L
k
l
IA
V1
V3
A
V2
FS
Osc
Rys. 5. Układ stanowiska pomiarowego.
AT- autotransformator; T – transformator; D- dławik; RN- bocznik; P- przekładnik prądowy; M- czujnik
indukcyjny; Osc – oscyloskop; V1- woltomierz cyfrowy z przetwornikiem wartości średniej; V2 – woltomierz
cyfrowy z przetwornikiem wartości skutecznej; V3 - woltomierz analogowy z przetwornikiem wartości średniej;
A – amperomierz elektromagnetyczny; Ac- amperomierz cęgowy; FS – fluksomierz synchroniczny.Tab.
1.
Pomiary prądu sinusoidalnego.
Metoda i wyniki odczytów
I U(I) [A]
Urel(I)
p =...........
%
1. pomiar spadku napięcia na
boczniku
U1 = .....................................
................................................ .................................................
U2 =......................................
................................................ ...............................................
2. amperomierzem EM z
przekładnikiem o I= .....
IA = .......................................
................................................ ................................................
3. amperomierzem cęgowym
IC = ......................................... ................................................ ................................................
4. czujnikiem indukcyjnym
U3 = ........................................
Imax = ................(wg wzoru 4.) ...............................................
................................................
Tab. 2. Wyniki pomiarów prądu odkształconego i błędy dodatkowe od kształtu przebiegu
I
Metoda i wyniki odczytów
A
I
dod
I pop
I
100
1. j. w.
2. j. w.
3. j. w.
4. j. w.
Uwaga! Za wartość poprawną prądu należy przyjąć wskazania woltomierza cyfrowego True
RMS
Tab. 3. Pomiary fluksomierzem synchronicznym wartości chwilowych prądu odkształconego.
L.p.
[mWb]
ix(ti) [A]
Ix[A]
1
.
.
50
Ix – wartość skuteczna prądu określona wg zależności (6).
7. Uwagi do opracowania wyników pomiarów i wniosków
1.
W przypadku pomiarów prądu sinusoidalnego, wyniki pomiarów należy podać z
niepewnościami wynikającymi z błędów podstawowych (granicznych) stosowanych
narzędzi pomiarowych. Dla zobrazowania oceny dokładności poszczególnych metod
pomiarowych, należy poszczególne wyniki pomiarów przedstawić graficznie na osiach
wartości napięć (rys. 6).
IX1
IX1+U(IX1)
IX2-U(IX2)
IX2
IX1-U(IX1)
IA-U(IA)
IA
IA+U(IA)
IC-U(IC)
IC
IC+U(IC)
IX3-U(IX3)
200
IX2+U(IX2)
210
220
230
IX3
IX3+U(IX3)
240
250
260
[A]
Rys. 6. Graficzne zobrazowanie wyników pomiarów prądu sinusoidalnego (przykład).
2.
W pomiarach prądu znacznie odkształconego dominującym źródłem
niepewności może być kształt przebiegu, a wtedy błędy podstawowe można uznać za
nieistotne. Tylko niektóre przyrządy mogą poprawnie mierzyć takie prądy, i to tylko
przy umiarkowanych odkształceniach. Są to amperomierz elektromagnetyczne i
woltomierze cyfrowe z przetwornikiem wartości skutecznej (tzw. True RMS). W
związku z tym, w obliczeniach błędów dodatkowych pomiarów prądu znacznie
odkształconego za wartość poprawną należy przyjąć wynik uzyskany ze wskazań
woltomierza True RMS.
8. Opracowanie wyników pomiarów
Pomiary dużych prądów sieciowych zwykle realizowane są metodą pośrednią.
Jedynie amperomierz cęgowy mierzy metodą bezpośrednią. W ćwiczeniu wykonano pomiary
prądu sinusoidalnego (niezniekształconego) i prądu odkształconego o przebiegu znacznie
odbiegającym od sinusoidy. W drugim przypadku pomiary miały na celu sformułowanie
oceny przydatności poszczególnych metod pomiarowych w pomiarach prądów
odkształconych.
Na dokładność pomiarów prądów sinusoidalnych wpływają głównie błędy podstawowe
przyrządów i przetworników tworzących układ pomiarowy. Zaś w pomiarach prądów
odkształconych mogą też wystąpić duże błędy dodatkowe (błędy kształtu), i szacowanie
dokładności pomiarów bez ich uwzględnienia nie daje wiarygodnych wyników. Dla
konkretnego przyrządu pomiarowego, czy układu pomiarowego, ocena błędu kształtu nie jest
łatwa, gdyż jego wartość jest uwarunkowana kształtem przebiegu czyli jego stopniem
odkształcenia (opisanym np. współczynnikiem kształtu).
Obliczanie niepewności pomiarów prądów sinusoidalnych
Obliczenie niepewności pomiaru metodą bezpośrednią (pojedynczym przyrządem)
czyli amperomierzem cęgowym polega na wyznaczeniu z jego błędu granicznego
niepewności standardowej (ur(I)= g(I)/ 3 ), a następnie niepewności rozszerzonej –
przyjmując współczynnik rozszerzenia k= 3 p (p - poziom ufności).
Metodę pośrednią pomiaru realizują trzy układy pomiarowe, w których przetwornikami
dużych prądów są:
 bocznik kl. 0,5
 przekładnik prądowy kl. 0,5
 czujnik indukcyjny M=(8,40,2)H (wartość uwzględnia błąd graniczy czujnika)
Do pomiarów sygnałów wyjściowych przetworników wykorzystywane są:
 multimetr cyfrowy „Metex”
 multimetr cyfrowy „Peak-Tech”
 multimetr analogowy V640, kl.0,5
 amperomierz elektromagnetyczny kl.0,5
Dokładności multimetrów podają wyciągi z ich instrukcji obsługi.
W pomiarach pośrednich, w pierwszej kolejności, liczy się niepewność standardową
łączna. Stosując prawo propagacji niepewności i uwzględniając równania pomiarów dla
stosowanych układów, otrzymuje się zależności
u r , (I)  u 2r (p)  u 2r (m) ,
u r ,  ( I) 
1
 g2 (p)   g2 (m) ,
3
w których: ur(p), ur(m), g(p), g(m) – są niepewnościami standardowymi i
błędami granicznymi przetwornika i przyrządu pomiarowego. Błędy graniczne
bocznika i przekładnika prądowego odpowiadają ich klasie, a względny błąd
graniczny czujnika indukcyjnego wynika z zapisu wartości jego indukcyjności
wzajemnej.
Licząc dalej niepewność rozszerzoną – Ur(I) = k ur,(I), należy przyjąć współczynnik
rozszerzenia k=2 - jeżeli wynik pomiaru ma być przedstawiony z poziomem ufności p=0,95.
Ocena niepewności pomiarów prądów odkształconych
Do pomiarów prądów odkształconych zastosowano też, oprócz wymienionych układów,
układ z przetwornikiem próbkującym sygnał napięciowy z czujnika indukcyjnego. Ze
wskazań przetwornika i dodatkowych obliczeń uzyskuje się zbiór próbek wartości
chwilowych mierzonego prądu, które służą do wyznaczenia wartości skutecznej prądu. Z
zasady działania tego układu wynika jego przydatność do pomiarów prądów odkształconych.
Jak wiemy, nie wszystkie przyrządy i układy mierzą poprawnie prądy odkształcone.
Które ze stosowanych w ćwiczeniu przyrządów i układów nie są przydatne w takich
pomiarach należy wykazać na podstawie porównania wyniku pomiaru uzyskanego układem
z miernikiem „true rms”, z wynikami uzyskanymi pozostałymi układami (też układem z
przetwornikiem próbkującym). Znaczące różnice wartości dają już podstawę to takiej oceny, a
którą należy sformułować we wnioskach sprawozdania.
Przykład: Zmierzono prąd przemienny 50Hz stosując układ z przekładnikiem prądowym
(kl. 1 ; i  500A / 5A ) i amperomierzem elektromagnetycznym (kl. 0,5 ; Iz=6A). Miernik
wskazał IA= 3.55A. Podać wynik pomiaru.
Wartość prądu: I = IA i =3.55A 100 =355A
Błąd graniczny amperomierza gI=kl. (Iz / IA)=0,5 (6A/3,55A)=0,845%
1
1
Niepewność standardowa łączna u r , (I) 
 g2 (I)   g2 (i ) =
0,85 2  12 =0,76%
3
3
Niepewność rozszerzona Ur(I)= k ur,(I) =2 0,76% =1,52%
Wartość bezwzględna niepewności U(I)= [Ur(I) I]/100%= (1,52% 355A)/100%=5,40A=5A
Wynik pomiaru I=(3555)A , p=0,95 ; Ur(I)= 1,5%