Znaczenie inwestycji w gospodarce narodowej i związany z tym problem podziału Dochodu
Narodowego na:
-
konsumpcję
-
konsumpcję i inwestycje - od stosunku tych nakładów zależy sytuacja w przyszłym roku (ruch
krzywej możliwości produkcyjnych i konsumpcyjnych). Sytuacja ta zależy również od tego, na co
inwestycje są przeznaczane - czy na poszukiwanie i wdrażanie nowych technik produkcyjnych
czy na powielanie starych.
Inwestycje są podstawowym czynnikiem rozwoju zarówno w skali makro jak i mikro np.
przedsiębiorstw.
W literaturze przedmiotu wyróżnia się dwa podstawowe ujęcia inwestycji tj. ujęcie monetarystyczne,
widziane przez pryzmat ruchu pieniądza, i ujęcie rzeczowe, widziane jako ruch dóbr.
Ujęcie rzeczowe inwestycji
Kamerschen, MCKenzie, Nordinelli: " przez inwestycje nie rozumiemy tu nabywania akcji czy
obligacji przez nabywców indywidualnych, lecz nabywanie dóbr inwestycyjnych przez
przedsiębiorstwa. Inwestycje są to zakupy dóbr kapitałowych, zakładów produkcyjnych,
wyposażenia, budynków mieszkalnych oraz zmiany zapasów, które mogą być użyte w produkcji
innych dóbr i usług." Jest to klasyczne ujęcie inwestycji.
Inwestycje portfelowe zostały więc wyłączone (zakup akcji lub obligacji), bo ich nie przybywa, a
jedynie zmieniają one właściciela.
Ujęcie monetarne inwestycji - dominujące w najnowszej literatury ekonomicznej.
Inwestycje to celowo wydatkowane środki inwestora (także przedsiębiorstwa) skierowane na
powiększanie jego dochodów. Przyjęcie opcji monetarnej w pojmowaniu inwestycji wynika z
immanentnego (nierozerwalnego) związku finansów i inwestycji.
Inwestycje to celowo wydatkowany kapitał przez inwestora (np. firmę) skierowany na powiększanie
jego dochodów.
Rodzaje inwestycji - klasyfikacja według różnych kryteriów:
Biorąc za kryterium podziału strukturę aktywów bilansu można wyróżnić:
1. inwestycje rzeczowe tworzące majątek rzeczowy (grunty, budynki, budowle, maszyny, środki
transportu)
2. inwestycje finansowe formułujące majątek finansowy (udziały, długoterminowe pożyczki, papiery
wartościowe)
3. inwestycje niematerialne stanowiące o wielkości i strukturze majątku niematerialnego i prawnego
(kształcenie, doskonalenie organizacji, patenty, licencje)
Szczególnie użyteczny w praktyce przedsiębiorstw produkcyjnych jest podział inwestycji rzeczowych
z punktu widzenia ich wpływu na poziom wielkości produkcji. Z punktu widzenia wpływu na
możliwości produkcyjne inwestycje dzielimy na:
1. odtworzeniowe - nie zmieniają zdolności produkcyjnej
2. rozwojowe - powodujące wzrost zdolności produkcyjnych
Ad. 1. Inwestycje odtworzeniowe powodowane są zużyciem majątku a ich zadaniem jest
zapewnienie zdolności produkcyjnych na dotychczasowym poziomie. Zużycie majątku, wyrażone
poziomem odpisów amortyzacyjnych, za pomocą rachunku kosztów jest wkalkulowane w cenę
wyrobów. W wyniku sprzedaży następuje odzyskanie jego równowartości. W praktyce ten sposób
inwestowania występuje rzadko w czystej postaci. W warunkach intensywnego postępu technicznego
zastępowanie zużytych środków identycznymi jest dalece ograniczone, często niemożliwe, a co
najważniejsze - ekonomicznie nieuzasadnione.
Ad. 2. Do jednej grupy inwestycji rozwojowych klasyfikujemy:
a) inwestycje nowe
b) rozbudowę
c) modernizację w sferze produkcyjnej
Ad. a. Inwestycje nowe w produkcyjnych działach gospodarki narodowej to budowa nowych
zakładów przemysłowych, budowlanych, rolnych, transportowych, linii energetycznych, szlaków
komunikacyjnych a także budowa nowych oddziałów i filii, lecz poza granicami lokalizacyjnymi
zakładów macierzystych.
Ad. b. Rozbudowa polega najczęściej na rozszerzeniu powierzchni produkcyjnej w granicach
lokalizacji zakładu lub w jego bezpośrednim sąsiedztwie. Rozbudową mogą być: obiekty produkcji
podstawowej, pomocniczej i ubocznej, nowe wydziały produkcji podstawowej lub pomocniczej do
wytwarzania dotąd nie produkowanych wyrobów a także nowe budynki i budowle
Ad. c. Modernizacja powoduje unowocześnienie środków trwałych zgodnie z wymogami postępu
technicznego. Przedmiotem inwestycji modernizacyjnych jest przedsiębiorstwo nie zaś branża czy
gałąź (branża jest określeniem węższym niż gałąź). Inwestycje modernizacyjne realizuje się w
zasadzie:
-
w istniejącym już podmiocie gospodarczym
-
w obrębie dotychczasowej powierzchni produkcyjnej
-
w granicach istniejącej już lokalizacji
-
przy danej strukturze, zabudowie itp.
co sprawia, że inwestycje te mają jednorazowy, niepowtarzalny charakter. Ponadto cechą pozytywną
tych inwestycji jest fakt, że dotyczą one przede wszystkim aktywnej części majątku firmy. Te cechy
powodują, że ich realizacja daje wzrost efektywności produkcji w relatywnie najkrótszym czasie
względem innych inwestycji rozwojowych.
Inwestycje dzielimy na:
-
konieczne - rokujące nadzieję na zwrot poniesionych kosztów czyli inwestycje w maszyny,
urządzenia i aparaturę decydujące o wielkości i jakości produkcji
-
tzw. zło konieczne inaczej murowańce lub obudowa inwestycji - nie przynoszą zysków ale są
konieczne np. hale produkcyjne
Proces inwestycyjny
Podstawowym podmiotem procesy inwestycyjnego jest inwestor zwany także przedsiębiorcą lub
decydentem.
Inwestor - osoba fizyczna, prawna, grupa osób czy też otwarta organizacja, która we własnym
imieniu podejmuje decyzje inwestycyjne i dysponująca kapitałem niezbędnym na pokrycie wydatków
związanych z przygotowaniem, realizacją i eksploatacją inwestycji oraz przyjmująca wpływy
finansowe wynikające z jej funkcjonowania.
Inwestor podejmując decyzje o lokalizacji inwestycji posługuje się rachunkiem inwestycji, który
zawiera podstawowe wielkości (nakłady, efekty i czas) stanowiące o racjonalności decyzji,
uwzględniając warunki pochodzące z otoczenia gospodarczego np. rynek, ceny itp. Podstawową
sprawą dla inwestora jest rentowność inwestycji, czyli relacja otrzymanego zysku z inwestycji do
zaangażowanego kapitału.
Inwestycje w socjalizmie i kapitalizmie
W ekonomii socjalizmu proces inwestycyjny to ogół czynności, podejmowanych przez podmioty
działające, i zdarzeń związanych z tworzeniem i powiększaniem zasobów środków trwałych. Jest to
ujęcie wąskie, gdyż obejmuje czynności związane z przygotowaniem i realizacją inwestycji zaś efekt
mierzony jest zmianami w zasobach środków trwałych. W tym przypadku proces inwestycji kończy
się na uruchomieniu inwestycji, nie zajmuje się natomiast jej eksploatacją.
W rynkowej gospodarce kapitalistycznej proces inwestycyjny obejmuje swym zakresem cykl
rozwojowy projektu inwestycyjnego zapoczątkowany pierwszymi wydatkami pieniężnymi a kończący
się ostatnimi wpływami z tytułu likwidacji obiektu.
Projekt inwestycyjny pojmowany jest szeroko jako czas życia projektu liczony od momentu
zapoczątkowania prac przygotowawczych, przez realizację i eksploatację inwestycji do momentu
likwidacji. Tylko całościowe ujęcie cyklu rozwojowego projektu inwestycyjnego daje podstawę do
racjonalnych decyzji. Celem inwestowania nie jest tylko tworzenie majątku lecz efektywna lokata
kapitału, która uwidacznia się dopiero przez ujęcie wszystkich wpływów i wydatków pieniężnych w
czasie życia projektu.
Złożoność procesu inwestycyjnego, liczebność faz oraz ich stopień szczegółowości są determinowane
wielkością, zakresem i rodzajem inwestycji. Stąd trudno o ogólny wzorzec w tym zakresie, jednak
zgodnie z opracowaną przez Międzynarodowe Centrum Studiów Przemysłowych UNIDO w Wiedniu
koncepcją cykl rozwojowy projektu inwestycyjnego obejmuje 3 fazy:
a) fazę przedinwestycyjną (informacyjną)
b) fazę inwestycyjną
c) fazę operacyjną (eksploatacyjną)
Ad. a. W fazie informacyjnej dla inwestora wyróżnia się następujące fazy:
1. identyfikacji możliwości inwestycyjnych (stadium możliwości) - ma ona za zadanie identyfikacją
kierunków inwestowania
2. wstępnej selekcji i określenia projektu (stadium przedrelizacyjne) - ma znaczenie wówczas, gdy
rentowność projektu jest wątpliwa i niektóre aspekty projektu wymagają szczegółowego
rozważenia
3. formułowania ostatecznej wersji projektu i ostatecznej oceny decyzji inwestycyjnych
Ostateczna wersja projektu powinna stanowić propozycję budowy projektu o:
-
określonej zdolności produkcyjnej
-
wyznaczonej lokalizacji
-
wykorzystującego określoną technikę i technologię w powiązaniu z określonymi surowcami i
materiałami
-
o znanych nakładach inwestycyjnych i kosztach produkcji oraz określonych dochodach ze
sprzedaży przynoszący określony zysk
W fazie przedinwestycyjnej jakość i niezawodność projektu są ważniejsze niż czynnik czasu.
Ad. b. Faza realizacji projektu inwestycyjnego rozpoczyna się w momencie podjęcia decyzji
inwestycyjnej i w fazie tej wyróżniamy 5 etapów:
1. przygotowania technicznego projektu (harmonogramu prac, szczegółowego projektu
inżynieryjno-budowlanego i technologicznego)
2. negocjacji i zawierania umów w sprawie finansowania projektu, dostaw maszyn i urządzeń,
zakupu usług, licencji, umów kooperacyjnych itp.
3. budowy projektu
4. szkolenia kadr
5. oddania inwestycji do eksploatacji
W fazie realizacji inwestycji czas ma znaczenie krytyczne, gdyż koszty zamrożenia środków
pieniężnych powiększają nakłady inwestycyjne. Koszty zamrożenia środków pieniężnych to stracone
odsetki od tych środków gdyby były ulokowane w banku.
Ad. c. Faza operacyjna trwa od rozpoczęcia produkcji na skalę handlową do likwidacji obiektu,
zakończenia okresu życia obiektu inwestycyjnego. Fazę tą dzielimy na dwa etapy:
1. etap dochodzenia do projektowanej zdolności produkcyjnej
2. etap pełnego wykorzystania zdolności produkcyjnych, oceniany jest on przez pryzmat wpływów i
wydatków
W fazie tej nie ma nakładów inwestycyjnych - są tylko koszty i przychody.
Przepływy środków pieniężnych w procesie inwestycyjnym
Cykl inwestycyjny rozpoczyna się wydatkowaniem środków pieniężnych na przygotowanie i
realizację inwestycji a kończy się wpływami ze sprzedaży likwidowanego obiektu. Pozostałe
przepływy gotówki w czasie to bieżące wydatki i wpływy związane z działalnością produkcyjną, które
stanowią o kosztach wytwarzania i przychodach ze sprzedaży produkowanych dóbr i usług.
Rozłożenie w czasie wpływów i wydatków związanych z przygotowaniem, realizacją i eksploatacją
inwestycji może przebiegać bardzo różnie i zależy od splotu czynników obiektywnych (rodzaj,
wielkość i zakres podejmowanej inwestycji) oraz czynników subiektywnych (np. organizacja
procesu).
Metody oceny - rachunek inwestycji
Warunkiem opłacalnej alokacji kapitału jest posługiwanie się poprawnymi metodami oceny
racjonalności inwestycji.
Procesowi rozwoju kapitału towarzyszy proces doskonalenia metod rachunek inwestycji.
Etapy rozwoju:
-
w XVI i XVII następował proces powstawania i rozwoju kapitału kupieckiego bankowego
-
rewolucja przemysłowa w okresie której nastąpił przełom w konstruowaniu metod oceny alokacji
kapitału. W tym okresie zostały sformułowane teoretyczne podstawy współcześnie stosowanych
współcześnie stosowanych metod rachunku inwestycji
-
eksplozja stosowania teoretycznego i praktycznego metod oceny projektów inwestycyjnych
nastąpiła w latach 50 i 60. W Polsce zapoczątkowany został rozwój metod rachunku inwestycji w
1950 roku a przełomowe lata dla dalszego rozwoju metod to:
- 1962 rok - obligatoryjnie wprowadzono rachunek inwestycji
- 1970 rok - 1974 rok - wprowadzenie WOGu czyli wielkich organizacji gospodarczych
-
obecnie upowszechniona jest teoria i praktyka rachunku inwestycji wypracowanego przez
ekonomistów zachodnich
Rachunek inwestycji daje odpowiedź na dwa podstawowe pytania:
1. Czy zasadne jest ekonomicznie podjęcie zaplanowanej inwestycji ? (absolutna ocena projektu)
2. Który z pośród realnych, czyli opłacalnych, wariantów (projektów) inwestycyjnych cechuje się
największą efektywnością, przy założeniu spełnialności równości systemu celów, otoczenia i
równego czasu planowania ? (relatywna ocena projektu)
Z punktu widzenia czynnika czasu wyróżnia się metody rachunku inwestycji:
1. statyczne
2. dynamiczne (zwane również wieloletnimi lub rozwiniętymi)
Ad. 1. Metody statyczne stosowane są zwykle we wstępnych fazach procesu inwestowania (stąd
ich orientacyjna rola) oraz do oceny mniejszych inwestycji przedsiębiorstw o stosunkowo krótszym
czasie realizacji i eksploatacji np. inwestycji modernizacyjnych. Cechą tych metod jest fakt, że nie
uwzględnia się w nich rozkładu płatności w czasie. Zaletą metod statycznych jest ich prostota,
komunikatywność i jasność formuły.
Ad. 2. Metody dynamiczne ujmują całościowo czynnik czasu i rozkład wpływów i wydatków
związanych z przygotowaniem, realizacją i eksploatacją inwestycji. Ich przeprowadzenie wymaga
dużej wiedzy teoretycznej i praktycznej. Poprawność tego rachunku jest funkcją dogłębnej
znajomości ekonomii i w miarę potrzeb ekonomiki branży której projekt dotyczy. Według przyjętych
kryteriów optymalizacji decyzji inwestycyjnych metody dzielimy je na:
1. metodę wartości zdyskontowanej netto
2. metodę wewnętrznej stopy procentowej
3. metodę annuitetową jako szczególną formę metody wartości zdyskontowanej netto
Metody rachunku inwestycji
Metody statyczne
Metody dynamiczne
m.in.:
m.in.:
1. rachunek porównawczy kosztów
1. rachunek wartości (nadwyżki)
2. rachunek porównawczy zysku
zdyskontowanej netto
3. rachunek porównawczy rentowności
2. rachunek wewnętrznej stopy procentowej
4. rachunek okresu zwrotu nakładów
3. rachunek annuitetowy
inwestycyjnych
Metody statyczne
Rachunek porównawczy kosztów jest stosowany często przy podejmowaniu decyzji
inwestycyjnych o charakterze odtworzeniowo - modernizacyjnym. Służy jako narzędzie wyboru
najlepszego wariantu spośród wariantów cechujących się identycznością korzyści (przychodów) a
zróżnicowaną wielkością ponoszonych kosztów. W tych warunkach kryterium racjonalności decyzji
jest minimum kosztów. Rachunek porównawczy kosztów zakresem czasowym obejmuje najczęściej
1 rok.
Zastosowanie rocznego rachunku kosztów wymaga zróżnicowania kosztów na:
1. roczne koszty inwestycyjne oznaczane K K
2. roczne koszty operacyjne (eksploatacyjne, zakładowe) oznaczane K O
Ad. 1
Koszty inwestycyjne roczne wyznacza amortyzacja (oznaczana jako A) oraz zysk
(oznaczany jako Z).
Przy linowym naliczaniu amortyzacji mamy A M R ,gdzie M - nakład inwestycyjny, R - wartość
n
końcowa po wyłączeniu obiektu z eksploatacji czyli tzw. reszta, n - przyjęty okres eksploatacji
inwestycji
Zysk liczy się w stosunku do przeciętnej sumy nabycia i zainstalowania obiektu inwestycyjnego oraz
wartości końcowej z uwzględnieniem przyjętej stopy zysku kalkulacyjnego ze wzoru Z M R * i ,
2
gdzie i - stopa zysku kalkulacyjnego.
Koszty inwestycyjne dane są wzorami i wynoszą:
-
z uwzględnieniem wartości końcowej K K M R M R * i
n
2
-
bez uwzględnienia wartości końcowej K K M M * i .
n
2
Ad. 2
Koszty operacyjne (eksploatacyjne, zakładowe) roczne obiektu inwestycyjnego
obejmują koszty osobowe, koszty materiałowe, koszty powierzchni produkcyjnej, energii, dozoru i
inne, a zatem poziom rocznych kosztów obiektu inwestycyjnego, oznaczony jako K i dany wzorem
K= KO + KK wynosi :
-
przy uwzględnieniu wartości końcowej K M R M R * i K O
n
2
-
bez uwzględnienia wartości końcowej K M M * i KO
n
2
Zakładając, że przedmiotem wyboru są dwa warianty realizacji inwestycji odtworzeniowej wariant nr
1 i nr 2 mamy matematyczny model rachunku porównawczego kosztów, który będzie miał postać:
-
przy uwzględnieniu wartości końcowej
M 1 R1 M 1 R1
M R2 M 2 R2
* i1 K O1 lub 2
* i KO2
n1
2
n2
2
-
bez uwzględnienia wartości końcowej
M1 M1
M
M
* i1 K O1 lub 2 2 * i K O 2
n1
2
n2
2
Przedmiotem realizacji będzie ten wariant, którego koszty całkowite będą mniejsze. Kryterium
wyboru jest K→min.
Warianty rocznego rachunku kosztów:
Wariant I
Mamy inną sytuację niż wyżej wyznaczona, mianowicie wyniki produkcji porównywanych wariantów
są wyraźnie zróżnicowane. W tej sytuacji posługujemy się techniką rachunku kosztów jak wyżej z tą
różnicą, że operujemy kosztami jednostkowymi a kryterium wyboru jest minimalizacja kosztu
jednostkowego, oznaczamy kj→min..
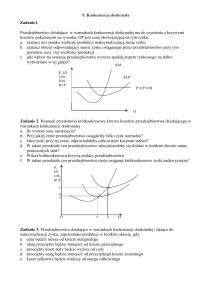
W praktyce może być sytuacja w której rozmiary produkcji trudno precyzyjnie ustalić a koszty stałe i
zmienne (operacyjne) są wyraźnie zróżnicowane. Wówczas musimy ustalić krytyczny poziom
produkcji, który określany jest przez punkt zróżnicowania kosztów alternatywnych rozwiązań.
Dla wariantów o numerach 1 i 2 mamy : K1=KS1+kO1*x
i
K2=KS2+kO2*x ,
gdzie: K - koszt
całkowity, kO - koszt zmienny jednostkowy (kO*x=KO ), KS - koszt stały ogółem, x - wielkość
(rozmiar) produkcji.
Ustalenie wielkości krytycznej wielkości produkcji wymaga spełnienia warunku K S1+kO1*x =
x
KS2+kO2*x z którego otrzymujemy, że
K S 2 K S1
.
k O1 k O 2
Wyszczególnienie
Wariant 1
Wariant 2
Koszty stałe ogółem (w tys. zł)
50 000
38 000
Koszty jednostkowe zmienne (w
17
20
tys. zł)
50000+17*x = 38000+20*x
stąd x
krytyczne=4000
Przy wielkości produkcji równej wartości krytycznej koszty całkowite w obu wariantach są
250 000
200 000
koszt
150 000
100 000
50 000
wariant nr 2
wariant nr 1
0
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
wielkość produkcji
jednakowe.
Graficznie wartość krytyczną wielkości produkcji wyznaczamy jako przecięcie obu funkcji kosztów. Z
wykresu wynika, że wariant nr 1 jest korzystniejszy dla rozmiarów produkcji przekraczających 4000
jednostek, a wariant nr 2 jest korzystniejszy dla wielkości produkcji nie przekraczającej 4000
jednostek.
Wariant II
Rachunek porównawczy kosztów może dać odpowiedz na pytanie czy ekonomicznie celowe jest
zastąpienie eksploatowanego środka trwałego (przed upływem czasu jego technicznego zużycia)
nowym, który cechuje się lepszymi parametrami.
Należy wówczas ustalić:
-
koszty inwestycyjne i zmienne (roczne) starego i nowego środka trwałego
-
przeciętne roczne zmniejszenie wartości końcowej starego obiektu, czyli reszty (oznaczonej R)
-
zysk kalkulacyjny liczony względem przeciętnej rocznej wartości końcowej starego obiektu
a następnie porównać KK i KO starego i nowego obiektu.
Wadą rocznego rachunku kosztów jako metody jest:
-
krótki okres czasowy
-
trudności związane z podziałem kosztów na stałe i zmienne
-
nie uwzględnianie przychodów - jest to główna wada
Rachunek porównawczy zysków - w praktyce jest stosowany rzadziej niż rachunek porównawczy
kosztów. Rachunek porównawczy zysków jako instrument oceny wariantów inwestycyjnych wiąże
przychody z kosztami ich uzyskania. Ograniczenie się w praktyce do rachunku porównawczego
kosztów może w pewnych warunkach prowadzić do błędnych decyzji np. nowe urządzenie techniczne
zapewnia wyższą jakość produktu i co za tym idzie wyższą cenę i zysk, wówczas nie można posłużyć
się wyłącznie rachunkiem porównawczym kosztów, gdyż koszty inwestycji tego urządzeni będą
wyższe.
G=E-K
,gdzie:
E - przychód z określonej działalności gospodarczej
K - koszty określonej działalności gospodarczej
W odniesieniu do pojedynczej inwestycji musi być zachowany warunek
G 0 , a porównując
alternatywne rozwiązania korzystniejszy jest wariant o wyższym poziomie zysku np. dla dwóch
wariantów o numerach 1 i 2, przy założeniu
G1 G2 ,
efektywniejszy jest wariant nr 1.
Odmiany rachunku porównawczego zysków w zależności od konkretnych uwarunkowań decyzyjnych:
1. przychód z produkcji w obu wariantach jest identyczny lub zbliżony
2. warianty mogą być różne pod względem mocy produkcyjnych, wówczas należy je ocenić według
kryterium maksimum zysku jednostkowego, czyli posłużyć się wielkościami jednostkowymi
przychodów i kosztów ich uzyskania
3. rozmiary produkcji obu wariantów trudno precyzyjnie ustalić, wówczas należy ustalić krytyczny
poziom produkcji przy którym wielkość zysku jest równa dla wszystkich rozważanych wariantów
(nr 1 i 2). W tym celu posługujemy się funkcją zysku następującej postaci:
G1 p1 * x k O1 * x K S1
G2 p 2 * x k O 2 * x K S 2
,gdzie:
p - cena jednostkowa
KS - stałe koszty w całym okresie
kO - koszt jednostkowy
p*x - przychód roczny, roczna wartość
sprzedaży
x - wielkość produkcji
kO *x + KS - koszty roczne
p1 * x k O1 * x K S1 p2 * x k O 2 * x K S 2
p1 * x p2 * x k O1 * x k 02 * x K S1 K S 2
x
K S1 K S 2
p1 p2 k 01 k O 2
Rachunek porównawczy rentowności – stosowany jest we wstępnych fazach przygotowania
decyzji inwestycyjnych. Najogólniej rentowność inwestycji to relacja otrzymanego z niej zysku do
zaangażowanego kapitału. W praktyce stosuje się różne konstrukcje miar rentowności inwestycji (ze
względu na różny zakres czasowy, różny pomiar zysku i zaangażowania kapitału).
Posłużmy się relacją rocznego zysku do zaangażowanego kapitału, a więc R
R
EK
*100 ,
DK
G
* 100 lub inaczej
DK
gdzie R – zysk w przyjętym okresie, DK – przeciętne zaangażowanie kapitału.
Istotną sprawą jest ustalenie DK czyli rzeczywistych rozmiarów zaangażowania kapitału, który
stopniowo zmniejszamy dzięki odpisom amortyzacyjnym. Stąd D K równa się: DK =M, D K
DK
M
lub
2
ER
, gdzie M – jednorazowy nakład inwestycyjny. Sposoby ustalania DK rzutują na rozmiary
2
kapitału i ostatecznie na poziom rentowności inwestycji. Stąd w praktyce problem ustalania D K
należy każdorazowo rozstrzygnąć w zależności od rodzaju inwestycji, ich cech jakościowych i
ilościowych.
Przy ocenie projektu inwestycyjnego stosuje się również stopę zwrotu kapitału własnego, będącą
relacją stopy zysku netto i kapitału własnego, daną wzorem RZ
GN
* 100 , gdzie RZ – stopa zwrotu
Q
kapitału własnego, GN – zysk netto.
Dokonując oceny konkretnego pojedynczego obiektu stosujemy kryterium
R Rmin ( Rmin - założone
przez inwestora), a oceniając dwa lub więcej nakładów inwestycyjnych stosujemy kryterium wyboru
wariantu
R max .
Rachunek porównawczy rentowności w powyższym ujęciu ma dwa zasadnicze ograniczenia:
1. nakłady na zakup i instalację inwestycji porównywanych wariantów powinny być równe lub
zbliżone
2. przewidywany czas eksploatacji wariantów równy lub zbliżony
Gdy te warunki nie są spełnione rachunek porównawczy rentowności należy zmodyfikować za
pomocą korekty o tzw. różnice inwestycyjne by sprowadzić warianty do porównywalności.
Rachunek rentowności stosuje się również do porównania ekonomiczności dotychczasowego i
nowego obiektu inwestycyjnego . Rachunek ten wyraża oszczędności kosztów z tytułu eksploatacji
nowego obiektu w relacji do przeciętnego zaangażowania kapitału tej inwestycji. dane jest to
wzorem
R
K A KB
, gdzie:
DKB
KA – koszty w przyjętym okresie dla dotychczasowego starego obiektu
KB – koszty w przyjętym okresie dla nowego obiektu
DKB – przeciętne zaangażowanie kapitału w nowy obiekt
Przykład
Dotychczasowa eksploatacja maszyn wymaga poniesienia kosztów średnio w roku 40 mln zł. Koszty
eksploatacji nowych maszyn wynoszą 25 mln zł. Nakłady inwestycyjne na nowe urządzenia i
maszyny wynoszą 90 mln zł. Jaka byłaby przeciętna rentowność inwestycji.
R
40 25 15 1
90
90 6
Rachunek zwrotu nakładów – chętnie stosowany przez decydentów, często nazywany kryterium
wyjściowym lokaty kapitału. Zadaniem tego rachunku jest ustalenie czasu zwrotu kapitału
zainwestowanego w konkretne zadania inwestycyjne.
T
M R
GŚR A
, gdzie:
T – okres zwrotu nakładów
M - całkowite nakłady inwestycyjne
GŚR – przeciętny roczny zysk
A – roczny odpis amortyzacyjny
Zazwyczaj inwestycje porównujemy
kryterium wyboru
T Tmax ale rozważając większą liczbę wariantów stosuje się
T min .
Przykład
Wyszczególnienie
Wariant 1
Wariant 2
Nakłady inwestycyjne
70 mln
90 mln
Wartość końcowa
nie ma
nie ma
Okres eksploatacji
5 lat
5 lat
Amortyzacja na rok
14 mln
18 mln
Zysk średni roczny
16 mln
25 mln
Zwrot roczny kapitału
30 mln
43 mln
T1
70
2,33 2lata _ 4mies
30
i
T2
90
2,09 2lata _ 1mies , tak więc wariant 2 jest
43
korzystniejszy.
Nierzadko w praktyce gospodarczej ekonomiści do ustalenia T stosują skumulowane szeregi czasowe
zwrotu kapitału.
Przykład
Lata
Roczny zwrot
Skumulowany zwrot
kapitału
kapitału
1
29 mln
29 mln
2
30 mln
59 mln
3
31 mln
90 mln
4
30 mln
120 mln
5
30 mlm
150 mln
METODY DYNAMICZNE
Problem ustalenie kosztu kapitału
Efektywność projektu inwestycyjnego wyznaczana jest z jednej strony przez rentowność a z drugiej
strony przez koszt kapitału zaangażowanego w finansowanie danego przedsięwzięcia. Koszt
kapitału w rachunku efektywności inwestycji występuje pod postacią stopy dyskontowej inaczej
stopa dyskontowa pełniąc rolę narzędzia sprowadzającego do porównywalności czasowej nakłady i
efekty z różnych okresów określana jest przez koszt kapitału.
W gospodarce centralnie planowanej koszt kapitału (stopa procentowa, stopa dyskontowa) był
ustalony centralnie i nosił miano minimalnej normy efektywności kapitału. Norma wyrażała
graniczną (minimalną) wielkość zysku jaką powinna zapewnić jednostka wydatkowanych nakładów
inwestycyjnych aby była efektywna z punktu widzenia interesu ogólnospołecznego (w latach 69-80
norma wynosiła od 8 do 12%)
Dostępność zasobów finansowych stanowi podstawowe kryterium podejmowania decyzji na
wszystkich etapach formułowania projektu inwestycyjnego.
Przy projektach dotyczących budowy nowych projektów zarówno nakłady inwestycyjne jak i
niezbędny (minimalny) poziom majątku obrotowego finansowane są ze środków własnych i obcych.
Finansowanie ze środków własnych
Finansowanie z formie
wkładów
Finansowanie w formie
udziałów i akcji
Finansowanie w formie
zysków zatrzymanych
- wkłady gotówkowe
- wkłady rzeczowe
Finansowanie ze środków obcych
Finansowanie w formie
pożyczek
Finansowanie w formie
kredytów
Finansowanie w formie
obligacji
Finansowanie w formie
leasingu
- kredyty bankowe
- kredyty dostawców
- kredyty odbiorców
Powyższy rysunek przedstawia klasyfikację form finansowania projektów inwestycyjnych.
Środki własne służące finansowaniu projektów inwestycyjnych polegających na tworzeniu nowych
przedsiębiorstw dostarczają inwestorzy w postaci wkładów pieniężnych (gotówki) lub w formie
rzeczowej tzn. niektórych składników środków trwałych np. gruntów pod budowę obiektu czy
środków transportu.
Środki na sfinansowanie projektów inwestycyjnych w przedsiębiorstwie już funkcjonujący
(rozbudowa, modernizacja lub odtworzenie składników majątku) pochodzą ponadto z zysków
zatrzymanych i amortyzacji .
Sposób gromadzenia środków własnych zależy od formy prawno-organizacyjnej przedsiębiorstwa,
wyróżniamy tu:
przedsiębiorstwa państwowe
przedsiębiorstwa własności prywatnej:
-
własności indywidualnej
-
spółki:
-
cywilne
-
handlowe:
-
osobowe tzn. spółka cicha, jawna i komandytowa (nie mają osobowości prawnej)
-
kapitałowe tzn. spółka z o.o. i akcyjna (mają osobowości prawną)
W spółkach osobowych kapitał udziałowy pochodzi z wkładów właścicieli. Wspólnicy mogą na mocy
umowy podjąć decyzję o podwyższeniu dotychczasowych udziałów lub o poszerzeniu grona
dotychczasowych współwłaścicieli.
W spółkach z o.o. gromadzenie kapitału zakładowego następuje przez wniesienie wkładu przez
założycieli. Podwyższenie kapitału zakładowego następuje poprzez sprzedaż udziałów
dotychczasowym lub nowym udziałowcom, co każdorazowo wymaga zmiany umowy spółki i wpisania
do rejestru handlowego.
W spółkach akcyjnych kapitał własny może być gromadzony i powiększany drogą emisji akcji
zwykłych oraz uprzywilejowanych. Emisja akcji zwykłych następuje z reguły po kursie (cenie)
sprzedaży różnym (najczęściej wyższym) od ich wartości nominalnej. Wynika to z tego, że zarówno
akcje stare jak i nowe dają ich posiadaczom tytuł własności do całego kapitału własnego spółki.
Kapitał ten ma złożoną strukturę obejmującą nie tylko kapitał akcyjny ale także kapitał dodatkowy,
pochodzący ze sprzedaży akcji zwykłych powyżej ich wartości nominalnej, oraz kapitał zapasowy
(rezerwowy), pochodzący z niepodzielonych zysków po opodatkowaniu tzw. zysków zatrzymanych.
Od akcji zwykłych przysługuje dywidenda gdy przedsiębiorstwo osiąga zysk a od akcji
uprzywilejowanych przysługuje stała określona dywidenda niezależnie od tego, czy przedsiębiorstwo
osiąga zysk czy nie. Gdy przedsiębiorstwo nie osiąga zysku dywidendy od akcji uprzywilejowanych
nie są wypłacane lecz kumulowane do czasu osiągnięcia zysku. Wówczas są wypłacane w pierwszej
kolejności tzn. przed dywidendami z akcji zwykłych. Uprzywilejowania akcji dotyczy także liczby
głosów z jednej akcji (może być kilka głosów z jednej a może nie być żadnego). Ponadto w
przypadku upadłości spółki akcyjnej posiadacze akcji uprzywilejowanych mają wcześniejszy dostęp
do majątku spółki niż posiadacze akcji zwykłych.
Finansowanie projektów inwestycyjnych ze środków obcych określane jest jako finansowanie za
pomocą długu lub kapitału obcego. Do podstawowych form finansowania inwestycji kapitałem obcym
należą:
-
długookresowe pożyczki
-
obligacje
-
leasing
Długookresowa pożyczka bankowa jest wygodną formą angażowania kapitału obcego bo realizowana
jest szybko i nie pociąga za sobą kosztów emisji. Przez zaciąganie pożyczek bankowych nie można
jednak uzyskać znacznego dopływu kapitału z zewnątrz bowiem banki, ograniczone przepisami
prawa bankowego nie, mogą pożyczyć jednemu pożyczkobiorcy większych kwot ponad określony
procent kapitałów własnych (najczęściej jest to 10%) a także nie chcą ze względu na zwiększony
stopień ryzyka opłacalności.
Pożyczki bankowe możemy podzielić na długookresowe, które w warunkach ustabilizowanej
gospodarki udzielane są na okres od 4 do 15 lat, choć występują pożyczki udzielane na okres od 1
do 3 lat oraz na okres powyżej 15 lat.
Pożyczki udzielane są na podstawie umowy. Przedmiotem pożyczki mogą być wyłącznie pieniądze.
Regułą jest, że pożyczki bankowe są odpłatne tzn. bank pobiera prowizję oraz odsetki za korzystanie
z kapitału. Sposób spłaty pożyczki bankowej określany w planie zwrotu pożyczki, a ten może
zawierać następujące warianty:
1. Płatność w równych ratach kapitałowych przez cały okres zaciągnięcia pożyczki powiększone o
odsetki od części kwoty pozostającej do spłacenia. Łącznie płatności z tytułu zaciągniętej
pożyczki w miarę upływu czasu ulegają zmniejszeniu.
2. Stałe kwoty płatności zadłużenia obejmujące zarówno ratę kapitałową jak i odsetki za dany
okres, przy czym kwota odsetek wraz ze spłatą pożyczki zmniejsza się, rośnie zaś udział raty
kapitałowej w stałej kwocie płatności.
3. W systemie zwanym „baloon” polegającym na tym, że pewnym momencie pozostające do
spłacenia łączne zadłużenie z tytułu rat kapitałowych oraz odsetek jest regulowane w całości.
Moment spłaty na ogół przypada w drugiej połowie okresu spłaty pożyczki.
Warunki spłaty pożyczki podlegają negocjacji i są przez to elastyczne pod względem możliwości
inwestora.
Oprocentowanie może być obliczane według stałej lub zmiennej (bardziej upowszechnionej obecnie)
stopy procentowej. Postawą oprocentowania pożyczki może być stopa procentowa międzybankowa
oferowana na rynku londyńskim lub stopa procentowa kredytu refinansowego ustalana przez bank
centralny (tak jest w Polsce) powiększana o marżę banku. Wysokość marży banku waha się od 0,75
do 3 i więcej punktów procentowych.
Jeżeli potrzebny jest kapitał obcy w szczególnie długim okresie (powyżej 15 lat) wówczas zaciąga się
pożyczki pod skrypt dłużny stanowiący dokument potwierdzający przyjęcie przez pożyczkobiorcę
kwoty pożyczki. Pożyczki te najczęściej udzielają towarzystwa ubezpieczeniowe. Pożyczki te są
najczęściej zabezpieczane hipotetycznie. Postawą ich udzielenia jest umowa.
Projekty inwestycyjne mogą być finansowane z kredytu: bankowego, dostawcy lub nabywcy
(przedpłaty) a także udzielane przez inne instytucje np. faktoringowe.
Kredyty bankowe są przeznaczane na sfinansowanie środków obrotowych ( kredyty krótko- i
średnioterminowe) oraz na wyposażenie nowych obiektów, a także na modernizację już istniejących
(kredyty średnio- i długoterminowe). Kredyty bankowe mogą być przeznaczane również na zakup
papierów wartościowych, patentów, technologii (w formie know how), prowadzenie badań oraz na
pokrycie kosztów gromadzenia kapitału (tzn. emisji akcji i obligacji).
Kredyt dostawcy jest udzielany przez producenta lub dostawcę określonych dóbr i usług. Ma on w
finansowaniu inwestycji szczególne znaczenie gdyż udzielany jest w formie kredytu
wyposażeniowego – w formie pieniężnej, połączony zazwyczaj ze zobowiązaniem się inwestora do
zakupu maszyn, urządzeń czy technologii u kredytobiorcy. Kredyty te mają zazwyczaj charakter
krótkookresowy.
Kredyt odbiorcy jest realizowany w formie przedpłat wnoszonych przez odbiorcę przyszłego dobra,
które ma powstać w rezultacie realizacji projektu inwestycyjnego. Dotyczy to głównie produktów
wytwarzanych na podstawie umów o dzieło. Kredyt tego typu ma pewne znaczenie w pozyskiwaniu
środków na finansowanie przedsięwzięć budowlanych.
W warunkach rozwiniętej gospodarki rynkowej duże przedsiębiorstwa poszukują środków na
sfinansowanie inwestycji na rynku kapitałowym przez emisję różnego rodzaju obligacji. Rozróżnia się
obligacje zabezpieczone i nie mające zabezpieczenia majątkowego.
Do obligacji zabezpieczonych zaliczamy obligacje hipoteczne – mają zabezpieczenie w wartości
nieruchomości będących własnością emitenta. Wartość emisji takich obligacji jest odnotowana jako
zobowiązanie z Księgach wieczystych nieruchomości. Obligacje hipoteczne stanowią dogodne źródło
finansowania projektów inwestycyjnych polegających przede wszystkim na budowie dużych obiektów
przemysłowych (handlowych) i turystycznych (hoteli, domów mieszkalnych) oraz inwestycji o
charakterze infrastrukturalnym.
Pozostałe obligacje stanowią papiery wartościowe za które inwestor odpowiada całym swoim
majątkiem. Są one emitowane na określone kwoty pieniężne z ustalonym terminem wykupu i
ustalonym oprocentowaniem, które zawsze jest przyjmowane na poziomie aktualnej w okresie emisji
stopy procentowej rynku kapitałowego powiększonej o premię za ryzyko rynkowe oraz za ryzyko
specyficzne dla inwestora emitenta.
Jeśli rynkowa stopa procentowa w okresie trwania zobowiązania się zmieni, to znajdzie ona wyraz w
kursie obligacji na wtórnym rynku papierów wartościowych (na giełdzie).
Finansowanie projektów inwestycyjnych może mieć charakter mieszany tj. w formie ich finansowania
za pomocą emisji akcji uprzywilejowanych. Akcje uprzywilejowane, podobnie jak akcje zwykłe,
powiększają kapitał akcyjny i nie podlegają obowiązkowi wykupu, z drugiej strony – podobnie jak
obligacje akcje uprzywilejowane zapewniają ich właścicielom stały dochód w postaci ustalonej z góry
dywidendy od ich wartości nominalnej. Jeżeli spółka wykazuje w danym roku zysk dywidendy od
akcji uprzywilejowanych wypłacane są w pierwszej kolejności przed dywidendami od akcji zwykłych,
także wtedy, gdy nie są wypłacane dywidendy od akcji zwykłych. Jednakże gdy spółka nie osiąga
zysku dywidendy od akcji uprzywilejowanych nie są wypłacane (są kumulowane do momentu
osiągnięcia przez spółkę zysku). Wypłat dywidendy od akcji uprzywilejowanych nie jest więc
bezwzględnym zobowiązaniem wobec akcjonariuszy, tak jak wypłata oprocentowania od obligacji.
Uwaga do zapamiętania: odsetki są elementem kosztów dla przedsiębiorstwa, a raty kapitałowe
płacone są z wypracowanego zysku.
Właściciele akcji uprzywilejowanych, w razie bankructwa, ponoszą większe ryzyko niż właściciele
obligacji, gdyż ich prawa jako właścicieli są uwzględniane w ostatniej kolejności po zaspokojeniu
należności wszystkich wierzycieli. Z tego powodu dywidenda od akcji uprzywilejowanych jest z góry
wyższa niż oprocentowanie obligacji tej samej spółki.
Akcje uprzywilejowane mogą zawierać klauzulę wymienialności na akcje zwykłe albo wykupu po
cenie emisyjnej (klauzula stosowana wówczas, gdy spółka akcyjna zamierza zmniejszyć
finansowanie kapitałem własnym (akcyjnym) i zastąpić go finansowaniem ze źródeł obcych.
Na rozwiniętych rynkach kapitałowych rośnie ranga leasingu jako jednej z form finansowania
inwestycji kapitałem obcym. W praktyce wykształciły się dwa podstawowe rodzaje leasingu:
1. leasing operacyjny (zwany także bieżącym)
2. leasing finansowy (zwany także kapitałowym)
Ad. 2
Leasing finansowy polega na odpłatnym korzystaniu z rzeczy w czasie zbliżonym do okresu
jej gospodarczej używalności. Długość tego okresu zależy od fizycznego zużycia dobra i postępu w
dziedzinie techniki powodującego jego ekonomiczne zużycie. Leasing finansowy ma charakter
średnio- lub długoterminowy (zwykle od 3 d 10 lat, dłuższe umowy ponad 10 lat stosowane są tylko
w USA).
W przypadku finansowego ruchomych środków trwałych leasingodawcę nie obowiązuje, poza
operacją finansowania, żadne inne świadczenie. Używający rzecz z umowy leasingu przyjmuje
obowiązek konserwacji, napraw, ewentualnie uprawnienia przysługujące bezpośrednio
leasingodawcy (np. z tytułu rękojmi czy gwarancji za wady rzeczy). Leasing umożliwiając
korzystanie ze środka trwałego stwarza prawo leasingobiorcy do jego przejęcia na własność po
zakończeniu okresu umowy. Występuje tu opcja zakupu sprzętu przez leasingobiorcę po zakończeniu
umowy.
Przedmiot leasingu może być wykazywany w bilansie leasingodawcy i wówczas jest to sytuacja
korzystna z punktu widzenia oszczędności podatkowych u leasingodawcy i leasingobiorcy (przedmiot
leasingu może być przypisany do jednej ze stron). U leasingodawcy przedmiot ulega umorzeniu a
kwoty amortyzacji wliczane są w ciężar kosztów działalności firmy, natomiast raty leasingowe
płacone przez leasingobiorcę stanowią przychód leasingodawcy, który po potrąceniu kosztów
finansowych (odsetek od kapitału i amortyzacji) stanowi zysk firmy leasingowej podlegający
opodatkowaniu. Ponieważ raty płacone w podstawowym okresie najmu znacznie przewyższają kwoty
odpisów amortyzacyjnych i dodatkowe koszty dawca osiąga duży zysk, a w konsekwencji znaczne
obciążenia podatkowe. Obciążenia te zmniejszają się po upływie podstawowego okresu najmu.
Odwrotnie wygląda sytuacja u leasingobiorcy , on bowiem w podstawowym okresie najmu ponosi
wysokie koszty leasingu wpływające na dochód (zmniejszające go) podlegający opodatkowaniu.
Zachodzi tu bowiem wyraźna rozbieżność między długością podstawowego okresu najmu a
oszczędnościami podatkowymi. Im krótszy okres najmu tym większa oszczędność podatkowa.
Zaliczenie przedmiotu umowy leasingu do aktywów leasingobiorcy nie wywołuje takich konsekwencji
podatkowych jak w sytuacji, gdy przedmiot umowy leasingu wykazuje w swoim bilansie
leasingodawca. Leasingobiorca nabywa prawo do odpisów amortyzacyjnych według obowiązujących
stawek dla danego typu sprzętu.
Przedmiotem umowy leasingu finansowego może być różnego rodzaju wyposażenie nowe i używane.
w przypadku nowo wytworzonych urządzeń musi być spełniony przynajmniej jeden z poniższych
warunków:
-
w treści umowy powinien znaleźć się zapis o przeniesieniu własności przedmiotu umowy na
leasingobiorcę po zakończeniu czasu trwania umowy
-
w umowie należy zastrzec prawo leasingobiorcy do zakupu przedmiotu umowy po jej
zakończeniu
-
okres obejmowania umowy powinien trwać co najmniej 75% przewidywanego czasu użytkowania
przedmiotu umowy
-
suma wartości bieżącej i minimalnych opłat leasingowych powinna stanowić co najmniej 90%
rynkowej wartości przedmiotu umowy
Leasing operacyjny zwany też eksploatacyjnym lub bieżącym – zbliżony od strony konstrukcji
cywilistycznej (prawnej) do umowy najmu i dzierżawy. Najczęściej zawierany jest na okres krótszy
niż wynosi ekonomiczne zużycie środka trwałego. Leasingodawca może więc zawierać kilka umów,
co pozwala na amortyzację przedmiotu własności i uzyskanie określonych korzyści finansowych.
Udostępniający ponosi zwykle pełne ryzyko dotyczące rzeczy, kosztów jej utrzymania, napraw i
ubezpieczenia oraz płaci związane z nią podatki. Przedmiot leasingu po upływie okresu umowy
powraca do leasingodawcy. Przy zastosowaniu tej umowy nie następuje przeniesienie prawa
własności do przedmiotu leasingu. Inne charakterystyczne cechy leasingu operacyjnego to:
-
przedmiotem transakcji są przeważnie dobra mogące być wielokrotnie użytkowane przez
kolejnych użytkowników np. samochody, komputery
-
umowy są zazwyczaj krótkoterminowe, zawierane maksymalnie na okres 3 lat
W przypadku leasingu operacyjnego to leasingodawca jest właścicielem przedmiotu leasingu i on
wykazuje go w swoim bilansie po stronie aktywów dokonując jednocześnie odpisów
amortyzacyjnych. Dla leasingobiorcy wydatki związane z leasingem (raty leasingowe, opłaty
manipulacyjne, prowizja leasingodawcy) są kosztem uzyskania przychodu, co ma zasadnicze
znaczenie z punktu widzenia obciążeń podatkowych. Leasingobiorca wpisując znaczne kwoty z tytułu
opłat leasingowych w koszty zmniejsza podstaw podatku dochodowego. Leasing bieżący ma
zazwyczaj charakter bezpośredni, ponieważ przebiega bez udziału firmy leasingowej (Leasing
finansowy ma charakter pośredni). Leasingodawcą jest zazwyczaj przedsiębiorstwo produkcyjne lub
handlowe, które oddaje określoną rzecz leasingobiorcy.
Leasing bieżący jest stosowany w celu zaspokojenia, przez korzystającego, przejściowego
zapotrzebowania na środki pracy uwarunkowanego np. szczególną organizacją przedsiębiorstwa,
sezonowością określonych rodzajów działalności gospodarczej, chęcią wypróbowania nowoczesnych
maszyn i urządzeń lub oczekiwaniem rychłego pojawienia się na rynku nowej generacji potrzebnych
środków pracy.
Udział leasingu w finansowaniu zakupów inwestycyjnych w 1994 roku
Irlandia
45 %
Austria
13 %
Słowenia
32 %
Włochy
13 %
Szwecja
19 %
Francja
13 %
Czechy
18 %
Holandia
12 %
Węgry
17 %
Belgia
9%
Portugalia
16 %
Dania
8%
Niemcy
14 %
Finlandia
8%
Wielka Brytania
15 %
Norwegia
6%
Szwajcaria
14 %
Grecja
4%
Hiszpania
13 %
Koszt pozyskania kapitału
Pozyskanie kapitału na finansowanie projektu inwestycyjnego ma zasadnicze znaczenie w rachunku
efektywności inwestycji i jest związane z określonymi kosztami. Kategoria kosztu kapitału znajduje
zastosowanie w rachunku finansowej opłacalności inwestycji – jest ona bowiem zasadniczym
parametrem wyznaczającym poziom stopy dyskontowej. Pojęcie dyskonta i wszystkie rachunki
związane z jego zastosowaniem wynikają z natury wartości tj. z zasady, że wartość ulega
pomnożeniu wraz z upływem czasu.
Kosztem kapitału nazywa się minimalną wymaganą stopę zwrotu, którą musi osiągnąć projekt
inwestycyjny aby zostały zaspokojone należne zobowiązania wobec właścicieli kapitału a także
zostały zapewnione warunki rozwoju przedsiębiorstwa zgodnie z zakładaną strategią.
Kapitał niezbędny do sfinansowania projektu inwestycyjnego pochodzi z różnych źródeł, mianowicie
ze sprzedaży akcji, wkładów właścicieli, sprzedaż obligacji, pożyczek i kredytów (leasingu) oraz z
części zysku netto (tzw. zysku niepodzielonego). Obliczanie kosztu kapitału wymaga określenia
następujących elementów (kroków):
I.
kosztu specyficznego dla każdego rodzaju źródła pozyskania kapitału
II.
struktury kosztu kapitału (udziału poszczególnych jego części (źródeł) w finansowaniu projektu
inwestycyjnego)
III.
średniej ważonej kosztu kapitału
Ad. I
Ustalenie kosztu specyficznego dla każdego rodzaju źródła pozyskania kapitału
1. Koszt kapitału akcyjnego zwykłego oblicza się wychodząc ze wzoru:
Vz
D zt
iz q
, gdzie:
V z - rynkowa wartość akcji zwykłej
D zt - dywidenda wypłacana w okresie t
iz
- stopa zwrotu wymagana przez akcjonariuszy, która jest jednocześnie kosztem kapitału
własnego
q - stała stopa wzrostu dywidendy
Po przekształceniach mamy:
iz
Dz
i z t q *100 , gdzie:
Vz
- koszt kapitału akcyjnego zwykłego wyrażony w %
2. Koszt kapitału akcyjnego gromadzonego w drodze nowej emisji akcji zwykłych zmieni się pod
wpływem dodatkowych kosztów poniesionych w związku z koniecznością:
- opracowania prospektu emisyjnego
- publikacji prospektu oraz sprawozdań finansowych
- wypłacania prowizji bankom za lokowanie akcji na rynku
Ponadto akcje z nowej emisji mają z reguły obniżoną cenę, która ma zwiększyć ich atrakcyjność
dla potencjalnych inwestorów.
Koszt kapitału akcyjnego zwykłego z nowej emisji wyniesie:
Dz
i zn t q *100 , gdzie:
Nn
i z n - koszt kapitału akcyjnego zwykłego z nowej emisji (w %)
N n - wpływy netto ze sprzedaży akcji nowej emisji
N n Vz K e z , gdzie:
K e z - koszt emisji i sprzedaży akcji zwykłych przypadający na jedną akcję
3. Koszt kapitału akcyjnego uprzywilejowanego określa się według formuły:
iu
iu - koszt kapitału akcyjnego uprzywilejowanego
Du - wartość rocznej dywidendy wypłacanej na jedną akcję uprzywilejowaną
Vu - wartość akcji uprzywilejowanej
Du
*100 , gdzie:
Vu
4. W wypadku nowej emisji akcji uprzywilejowanych koszt kapitału uzyskanego tą drogą kapitału
wyniesie:
iun
Du
*100 , gdzie:
Nu
n
iu n
- koszt kapitału akcyjnego uprzywilejowanego z nowej emisji
N u n - wpływy netto ze sprzedaży nowej emisji akcji uprzywilejowanych
N un Vu K eu , gdzie:
K eu - koszt emisji i sprzedaży akcji uprzywilejowanych przypadający na jedną akcję
5. Koszt kapitału własnego gromadzonego z tzw. zysku zatrzymanego (niepodzielonego) szacowany
jest na poziomie kosztu kapitału zwykłego, a więc:
iw i z
, gdzie:
i w - koszt kapitału własnego tworzonego z zysku zatrzymanego
6. Obliczenie kosztu kapitału pożyczonego wymaga uwzględnienia tzw. oszczędności podatkowej.
Odsetki płacone od tego kapitału stanowią bowiem element kosztów uzyskania przychodu
zmniejszających podstawę wymiaru podatku dochodowego.
Koszt kapitału pochodzącego z pożyczek oraz z kredytu bankowego oblicza się według formuły:
ik p1 s , gdzie:
i k - koszt kapitału pożyczonego w formie pożyczki lub kredytu bankowego
p - stopa oprocentowania kapitału pożyczonego
s - stopa podatku dochodowego wyrażona ułamkiem
7. Skorygowana wartość liczbowa obligacji określana jest według formuły:
Vo Po (1
m io
*
),
12 100
gdzie:
Vo - skorygowana wartość rynkowa obligacji
Po - rynkowa cena obligacji
i o - stopa oprocentowania obligacji
m
- liczba miesięcy, które upłynęły od ostatniej wypłaty odsetek
Koszt pozyskania kapitału w drodze pożyczki obligacyjnej wyniesie: io
O
(1 s ) *100 , gdzie:
Vo
i o - koszt kapitału ze sprzedaży obligacji
O
- wartość rocznych odsetek od obligacji
8. Koszt pozyskania kapitału w formie leasingu finansowego z opcją zakupu przedmiotu, która
zwiększa aktywa leasingobiorcy (przedmiot leasingu jest wykazywany w aktywach
leasingobiorcy), wynosi:
il pr pl * 1 s , gdzie:
- koszt pozyskania kapitału w formie leasingu finansowego
il
p r - stopa procentowa od kapitału udostępnionego w formie leasingu finansowego
p l - marża pobierana przez firmę leasingową wyrażona stopą procentową
9. Średnio ważony koszt kapitału wyraża się wzorem:
i s i z * u z i zn * u zn iu * u u iun * u un i w * u w ik * u k io * u o il * u l , gdzie:
is - średnio ważony koszt kapitału
u z , u zn , u u , u un , u w , u k , u o , u l - udział poszczególnych składników kapitału w ogólnej jego wartości ,
wyrażony w formie ułamka
Metoda wartości bieżącej (zdyskontowanej) netto oznaczana NPV (Net Present Value) lub Co
należy do metod podstawowych. Zdyskontowaną wartość netto inwestycji definiuje się jako sumę
zdyskontowanych na określony moment czasowy różnic wpływów i wydatków związanych z daną
inwestycją. Według niemieckich autorów H.Blohm'a i K.Lüder'a bieżącą wartość netto inwestycji w
punkcie czasowym t=0 definiuje się jako:
-
zdyskontowaną wartość przepływów pieniężnych netto
-
zdyskontowaną nadwyżkę netto z uwzględnieniem wartości likwidacyjnej i nakładów
inwestycyjnych
Formuła podstawowa ustalania wartości zdyskontowanej netto przedstawia się następująco:
n
C o et at * q t ,gdzie:
t 0
Co - zdyskontowana wartość netto
et
- wpływy w roku t
at
- wydatki w roku t
q t - współczynnik dyskontowy, gdzie: q 1 i
Metoda ta może służyć ocenie racjonalności pojedynczej inwestycji wówczas C o 0 . Dodatnia
bieżąca wartość netto informuje, że stopa rentowności badanego przedsięwzięcia rozwojowego jest
wyższa od stopy minimalnej (granicznej) określonej przyjętą do rachunku stopą dyskontową.
Oznacza to, że każda inwestycja charakteryzująca się wartością C o 0 (lub przynajmniej C o 0 )
może być realizowana, gdyż jest efektywna z punktu widzenia interesu firmy. Ujemna wartość
Co oznacza, że taką alternatywę należy odrzucić gdyż jest ona nieracjonalna z punktu widzenia
inwestora.
Oceniając kilka wariantów przy użyciu tej metody stosujemy jako kryterium wyboru maksymalizację
Co . Dla celów praktycznych należy skonkretyzować ten rachunek. Jeżeli Co obejmuje okres
wieloletni a wpływy i wydatki rozkładają się na poszczególne lata to zachodzi potrzeba
zdyskontowania oddzielnie dla każdego roku przepływów pieniężnych netto (Net Cash Flow)
będących różnicą między strumieniami wpływów i wydatków
et at . Suma zdyskontowanych
wielkości w okresie objętym rachunkiem odpowiada wartości zaktualizowanej netto. Stosując
symbolikę angielską możemy zapisać:
NPV = NCF0*a0 + NCF1*a1 + NCF2*a2 + ... + NCFn*an , gdzie:
NPV = Co - zaktualizowana wartość netto
NCFt - przepływy pieniężne netto w kolejnych latach okresu obliczeniowego
at q t 1 i
t
1
1 i t
- współczynnik dyskontowy
t = 0, 1, 2, ... , n - poszczególne lata okresu obliczeniowego
Widzimy, że poziom tego współczynnika, jak wynika z jego konstrukcji, zależy od poziomu stopy
dyskontowej i czasu obliczeniowego.
Zbieżność symboli: at w formule NPV oznacza współczynnik dyskontowy a w formule Co symbol at
oznacza wydatki w określonym roku. Dalej zostajemy przy oznaczeniu q -t dla współczynnika
dyskontowego. Przyjmując at = q-t uwzględniamy relatywny spadek wartości przepływów w
kolejnych latach obliczeniowych.
Ustalenie przepływów pieniężnych (różnic między wpływami i wydatkami w poszczególnych latach
okresu obliczeniowego) wymaga uwzględnienia następujących założeń:
1. nakłady inwestycyjne traktujemy jako wydatki
2. nakłady na odtworzenie czy modernizację środków trwałych w okresie obliczeniowym traktuje się
również jako wydatki
3. niektóre składniki nakładów należy ustalać nie według rzeczywistej wartości lecz kosztów
utraconych korzyści
4. amortyzacji nie traktuje się jako wydatku, co oczywiście powiększa NCF
5. zmiany kapitału obrotowego netto uwzględnia się w rachunku jako "+" czyli przychody lub "-"
czyli wydatki
6. wydatkami firmy są również wszelkie podatki, odsetki i raty kapitałowe
7. wartość likwidacyjna, zwłaszcza budynków, budowli i ziemi oraz odzyskany majątek obrotowy
traktuje się jako wartość netto w końcu okresu obliczeniowego
Wpływy i wydatki dyskontuje się na rok t=0 tj. rok bezpośrednio poprzedzający pierwsze płatności.
Współczynnik dyskontowy dla t=0 równa się 1. Okres dyskontowania powinien być równy okresowi
realizacji i użytkowania obiektu.
Precyzyjne określenie tych składników, a zwłaszcza okresu eksploatacji, jest w praktyce niezmiernie
trudne. Dlatego też w praktyce bierze się najczęściej pod uwagę okres użytkowania
najważniejszego, podstawowego dla danej działalności gospodarczej składnika.
W procesie wyboru decyzji inwestycyjnych spośród dopuszczalnych kryterium maksymalizacji
wartości zdyskontowanej netto
opiera się na wielkości absolutnej, a tym samym nie informuje precyzyjnie o różnicach w poziomie
rozważanych sposobów wykorzystania kapitału. Wobec tego wskazane jest posługiwanie się
wskaźnikiem wartości zaktualizowanej. Posługując się symboliką angielską wskaźnik ten oznaczany
NPVR (Net Present Value Ratio) jest miarą stopy zysku i wyraża się wzorem: NPVR
NPV
0,
PVI
gdzie:
NPVR - zdyskontowana stopa zysku
NPV - zdyskontowana wartość netto
PVI - bieżąca (zdyskontowana) wartość wymaganego nakładu inwestycyjnego
Kryterium wyboru projektu inwestycyjnego jest maksymalizacja wskaźnika NPVR czyli
maksymalizacja bieżącej (zdyskontowanej) stopy nadwyżki finansowej. Wydaje się, że to kryterium
wyznaczające bieżącą wartość nadwyżki netto z jednostki kapitału może pełnić w sytuacjach
decyzyjnych rozstrzygającą rolę.
Metoda wewnętrznej stopy procentowej (wewnętrzna stopa zwrotu Interne Zinsfuβ - Metode –
IRR).
Dotychczas w obliczeniach przyjmowaliśmy określoną, przyjętą przez inwestora kalkulacyjną stopę
zysku (procentową, dyskontową) ozn. „i”, która wyraża przyjętą, graniczną, minimalną wielkość
zysku od zaangażowanego kapitału.
Czy możliwe jest ustalenie faktycznej stopy zysku od wyłożonego kapitału, a następnie porównanie
jej z przyjętą minimalną stopą zysku ?
Wewnętrzna stopa procentowa jest odpowiednikiem stopy dyskontowej, przy której zaktualizowana
wartość wydatków pieniężnych równa się zaktualizowanej wartości wpływów pieniężnych. Jest to taki
poziom stopy dyskontowej, przy której zaktualizowana wartość netto równa się zero, czyli NPV = 0.
NCF0*a0 + NCF1*a1 + NCF2*a2 + ... + NCFn*an = C0 = 0 , gdzie:
NCFt – przepływy pieniężne netto w kolejnych latach okresu obliczeniowego (NCF t = et – at)
a t q t
n
e
t 0
t
1
1 i t
- współczynnik dyskontowy
a t * q t 0
e0 a0 e1 a1 e2 a2
e an
... n
0
0
1
2
1 i 1 i 1 i
1 i n
, gdzie:
et – wpływy w roku t
at – wydatki w roku t
Zakładamy, że nakłady inwestycyjne są wydatkowane jednorazowo w roku zerowym, możemy więc
zapisać:
e1 a1 e2 a2
e a
... n nn M 0 , gdzie:
1
2
1 i 1 i
1 i
M – nakłady inwestycyjne rozumiane jako wydatek roku dyskontowego tzw. zerowego
et – wpływy w poszczególnych latach użytkowania inwestycji
at – wydatki w poszczególnych latach użytkowania inwestycji
Uwzględniając wartość likwidacyjną majątku możemy zapisać:
e1 a1 e2 a2
e a
R
... n nn
M 0 , gdzie:
1
2
1
i
1 i 1 i
1 i
R – wartość likwidacyjna majątku
Wewnętrzną stopę procentową oznaczamy ir a jej poziom możemy ustalić metodą matematyczną i
graficzną.
Ustalanie ir metodą matematyczną – kalkulacja przebiega w następujący sposób:
-
przygotowujemy tablicę przepływów pieniężnych
-
zakładamy prawdopodobny poziom stopy dyskontowej, przy której C0 byłoby zbliżone do zera
-
obliczamy dla tego poziomu stopy dyskontowej zdyskontowaną wartość netto C 0
-
gdy C0 > 0 obliczenia powtarzamy zmieniając odpowiednio wartość stopy dyskontowej
-
gdy nadal C0 > 0 to w dalszym ciągu podwyższamy stopę dyskontową aż do uzyskania C0 < 0
-
gdy ujemne i dodatnie wartości C0 będą zbliżone do zera można precyzyjnie (tym precyzyjniej im
bliższe zera są wartości C0 )ustalić ir według wzoru:
ir i1
C01 (i2 i1 )
, gdzie:
C01 C02
ir – wewnętrzna stopa procentowa
i1 – stopa dyskontowa niższa, dla C0 > 0
i2 – stopa dyskontowa wyższa, dla C0 < 0
C01 i C02 – wartość zdyskontowana netto odpowiednio dla niższego i wyższego poziomu stopy
dyskontowej
Należy pamiętać, ażeby i1 oraz i2 nie różniły się więcej niż o jeden punkt procentowy.
Ustalanie ir metodą graficzną
Ustalając graficznie poziom wewnętrznej stopy procentowej przyjmuje się dwa różne poziomy stopy
dyskontowej i1, i2 oraz wyznaczone dla nich odpowiednio C01 , C02. Odkładamy dodatnią i ujemną
wartość C0 na osi odciętych a na osi rzędnych poziomy stopy dyskontowej. Linia łącząca punkty o
współrzędnych (C01, i1) i (C02, i2) przecina oś rzędnych w punkcie dla którego C 0 = 0 a więc
wyznaczone i = ir.
Należy zwrócić uwagę na to, że wewnętrzna stopa procentowa ir:
-
wyraża rzeczywistą stopę zysku nakładu inwestycyjnego
-
może być stosowana do ustalania warunków kredytowych, gdyż określa maksymalną stopę
oprocentowania kredytu, którą inwestor może zapłacić nie powodując strat ani też nie osiągając
zysku
-
spełnia rolę narzędzia oceny racjonalności decyzji inwestycyjnej:
ir i tzn. gdy wartość wewnętrznej
a. projekt inwestycyjny może być przyjęty do realizacji gdy
stopy procentowej jest wyższa lub przynajmniej równa granicznej stopie zysku, będącej
najniższą do przyjęcia stopą zysku od zainwestowanego kapitału (minimalna, graniczna stopa
zysku odpowiada poziomowi stopy procentowej szacunkowej lub alternatywnej)
b. rozpatrując szereg wariantów inwestycyjnych kryterium wyboru wariantu jest i r → max.
Zadanie
Przedsiębiorstwo rozważa ekonomiczną zasadność realizacji nowej inwestycji. cechy technicznoekonomiczne tego przedsięwzięcia opisuje poniższa tabela.
Planowane nakłady inwestycyjne:
Wyszczególnienie
Grunty
Budynki i budowle
Inne aktywa trwałe i
Lata
1995
1996
1997
1998
1999
60 200
-
-
-
60 200
2 000
-
21 000
40 000
25 000
88 000
50 000
60 000
101
211
000
000
100
126
359
000
000
200
obrotowe
Razem
62 200
71 000
Przewiduje się rozpoczęcie eksploatacji inwestycji w 1997 roku na poziomie 20% zdolności
produkcyjnych. Zakłada się, że ostatnim rokiem funkcjonowania inwestycji będzie rok 2003. Wartość
likwidacyjną szacuje się na 240 000. W okresie użytkowania inwestycji przewiduje się określony
rozkład wpływów i wydatków (tabela poniżej).
Przewidywane wpływy i wydatki strumieniowe inwestycji:
Wyszczególnienie
Lata
1997
Przychody ze sprzedaży
36 000
1998
180
1999
188
2000
190
2001
170
2002
165
2003
160
Koszty operacyjne
000
000
000
000
000
000
130
120
123
125
130
130
000
000
000
000
000
000
- 1 800
- 900
- 300
28 000
Zmiana zapasu środków
-
-
-
+ 20
obrotowych netto
000
Podatek dochodowy
-
-
20 400
20 000
11 200
7 200
5 200
Stopa dyskontowa wynosi 10%, inwestycja jest finansowana ze środków własnych firmy.
Rozwiązanie zadania z wykładu nr 10
Wyszczególnienie
A. Wpływy pieniężne:
1. dochody ze sprzedaży
2. inne dochody
Lata
1995
1996
1997
-
-
36 000
-
-
36 000
-
1998
1999
2000
2001
2002
2003
180
188
190
170
165
400
000
000
000
000
000
000
180
188
190
170
165
160
000
000
000
000
000
000
-
-
-
-
-
240
000
B. Wydatki pieniężne:
1. nakłady inwestycyjne
2. zmiany stanu środków
62 200 71 000
62 200 71 000
-
-
128
257
141
143
136
137
115
000
000
300
300
200
200
200
100
126
000
000
-
obrotowych netto
3. koszty operacyjne
4. podatek dochodowy
C. Przepływy pieniężne (A - B)
D. Współczynnik dyskontujący dla i =
+1
+ 900
+ 300
-
-
-
-
-
- 20
800
-
-
28 000
000
130
120
123
125
130
130
000
000
000
000
000
000
20 400 20 000 11 200
-
-
-
-
7 200
5 200
- 62
- 71
- 92
- 77 46 700 46 700 33 800 27 800
284
200
000
000
800
800
0,909
0,826
0,751
0,683
0,621
0,564
0,513
0,466
0,424
E. Wartość zdyskontowana netto (C *
- 56 -58 646 -69 092 -53 137 29 001 26 339 17 339 12 955
120
D)
540
755
F. Skumulowana wartość
- 56
- 115
-184
-237
-208
- 182
-164
zdyskontowana netto
540
186
278
415
414
075
736
10%
-151 -31 026
781
Metoda annuitetowa (rocznej nadwyżki netto) – jest ona powiązana z metodą zdyskontowanej
wartości netto, a ściśle jest jej odwrotnością. O ile metod wartości zdyskontowanej netto informuje
nas o sukcesie w ujęciu całkowitym o tyle metoda annuitetowa określa przeciętny roczny dochód. A
więc interesuje nas w jaki sposób można ustalić wielkość przeciętnej rocznej nadwyżki netto tzw.
annuitetu. Formuła ustalania wartości annuitetowej przyjmuje następującą postać:
d Co
q n q 1 , gdzie:
qn 1
d – annuitet
q n q 1
q n 1
-
współczynnik annuitetowy (czynnik przeliczeniowy) przyszłej wartości płatności
rocznej przy stopie
procentowej „i” oraz „n” latach
Warunkiem efektywności inwestycji w rachunku annuitetowym jest spełnienie nierówności d 0
Kryterium wyboru najlepszego projektu spośród rozważanych rozwiązań jest d → max. Inwestor
zwykle zainteresowany jest kalkulacją rocznej nadwyżki netto z planowanej inwestycji gdy korzysta
z kredytu bankowego. Pyta wówczas czy coroczna nadwyżka z tytułu użytkowania inwestycji pozwoli
na spłatę kredytu wraz z odsetkami. Ujmując inaczej problem pytamy jak musi być wielka coroczna
nadwyżka netto z inwestycji aby przy założonej stopie procentowej zapewniła w ciągu nlat zwrot
zaangażowanego kapitału. Wykorzystujemy wówczas formułę:
d M
i (1 i ) n
, gdzie:
(1 i ) n 1
M – nakład inwestycyjny początkowy
Ocena efektywności inwestycji jest również możliwa poprzez porównanie przeciętnych rocznych
wpływów z inwestycji i przeciętnych rocznych wydatków. Kryterium rachunku jest
JE – przeciętne roczne wpływy z inwestycji, dane wzorem: JE e R
JE JA , gdzie:
i
, gdzie:
(1 i ) n 1
e – roczne wpływy
R – wartość likwidacyjna
JA – przeciętne roczne wydatki związane z inwestycją, dane wzorem: JA a M
i(1 i) n
, gdzie:
(1 i) n 1
a – roczne wydatki eksploatacyjne
M – nakłady inwestycyjne
Zadanie
Zarząd spółki analizuje możliwość zakupu urządzenia według dwóch projektów. Projekt I cechuje się
równą nadwyżką roczną, projekt II natomiast przewiduje różny strumień przepływów pieniężnych.
Stopa dyskontowa dla inwestycji wynosi 9%. Obliczyć skumulowaną wartość zdyskontowaną netto.
Projekt I:
-
roczna nadwyżka finansowa
-
nakład inwestycyjny
10 000
20 000
Projekt II:
-
nadwyżka finansowa:
1 rok
2 rok
20 000 15 000
-
3 rok
4 rok
5 rok
5 000
5 000
2 000
nakład inwestycyjny
30 000