napięcie sinusoidalne

Podstawy
Elektrotechniki i Elektroniki
Opracował: Mgr inż. Marek Staude
Część 2
Analiza obwodów w stanie
ustalonym przy wymuszeniu
sinusoidalnym
Przypomnienie ostatniego wykładu
• Prąd i napięcie
• Podstawowe pojęcia dotyczące obwodów
• Podstawowe rodzaje połączeń elementów
• Źródła napięcia i prądu
• Rezystor oraz rezystancja
• Prawo Ohma
• Prawa Kirchhoffa
1
17
Pojęcia i podstawy matematyczne
Liczby zespolone
Pulsacja
Częstotliwość
Podstawy trygonometrii
2
17
Sygnał sinusoidalny
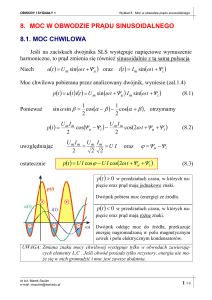
Parametry sygnału sinusoidalnego Sygnały sinusoidalne zwane również harmonicznymi są opisane w dziedzinie czasu
następującym wzorem (w opisie przyjęto oznaczenie sygnału napięciowego)
u(t) = Um sin(ωt + ψ)
Wielkości występujące w opisie mają następujące nazwy i oznaczenia:
u(t) - wartość chwilowa napięcia
Um - wartość maksymalna (szczytowa) napięcia zwana również amplitudą
ψ - faza początkowa napięcia odpowiadająca chwili t = 0
ωt + ψ - kąt fazowy napięcia w chwili t
f = 1/T - częstotliwość mierzona w hercach (Hz)
T - okres przebiegu sinusoidalnego
ω - pulsacja mierzona w radianach na sekundę.
Wartości chwilowe sygnałów oznaczać będziemy małą literą a wartości maksymalne, skuteczne i wielkości operatorowe dużą.
Rysunek na slajdzie piątym przedstawia przebieg sygnału sinusoidalnego napięcia z oznaczeniami poszczególnych jego parametrów.
Oś odciętych ma podwójne oznaczenie: czasu oraz fazy (aktualny kąt fazowy).
33
5
17
Wartość skuteczna sygnału okresowego
Przebiegi zmienne w czasie dobrze charakteryzuje wartość skuteczna. Dla przebiegu okresowego f(t) o okresie T jest ona definiowana w postaci
Łatwo udowodnić, że wartość skuteczna przebiegu okresowego nie zależy od wyboru fazy początkowej. W przypadku przebiegu sinusoidalnego
napięcia
u(t) = Um sin(ωt + ψ)
jest równa
U = Um/√2
a w przypadku prądu sinusoidalnego
i(t) = Im sin(ωt + ψ)
I = Im/√2
Dla sygnału sinusoidalnego wartość skuteczna jest więc √2 razy mniejsza niż jego wartość maksymalna. Należy zauważyć, że napięcie stałe u(t) =
U jest szczególnym przypadkiem sygnału sinusoidalnego, dla którego częstotliwość jest równa zeru f = 0 a wartość chwilowa jest stała i równa
u(t) = Um sin(ωt + ψ) = U
Jest to ważna właściwość, gdyż dzięki temu metody analizy obwodów o wymuszeniu sinusoidalnym mogą mieć zastosowanie również do
wymuszeń stałych przy założeniu f = 0 . Dla sygnału stałego wartość maksymalna i skuteczna są sobie równe i równają się danej wartości stałej.
43
5
17
Sygnał sinusoidalny
53
5
17
Wartość skuteczna sygnału okresowego
63
5
17
Stan ustalony obwodu
Metoda symboliczna liczb zespolonych analizy obwodów RLC w stanie ustalonym Analiza obwodów zawierających elementy
RLC przy wymuszeniu sinusoidalnym napotyka na pewne trudności związane z wystąpieniem w opisie cewki i kondensatora
równań różniczkowych. Trudności te łatwo jest pokonać w stanie ustalonym. Stanem ustalonym obwodu nazywać będziemy taki
stan, w którym charakter odpowiedzi jest identyczny jak charakter wymuszenia, to znaczy odpowiedzią na wymuszenie
sinusoidalne jest odpowiedź również sinusoidalna o tej samej częstotliwości choć o różnej amplitudzie i fazie początkowej.
Dla stanu ustalonego obwodu wprowadzona zostanie metoda liczb zespolonych, zwana również metodą symboliczną,
sprowadzająca wszystkie operacje różniczkowe i całkowe do działań algebraicznych na liczbach zespolonych.
7
17
Rezystor
Rezystor (opornik) jest elementem pasywnym.
Posiada on tylko jedną cechę (parametr) go opisującą – rezystancję (opór lub
oporność). Parametr ten oznaczamy literą R.
Jednostką rezystancji jest om (Ω).
Wartość rezystancji mierzymy omomierzem.
Odwrotność rezystancji nazywamy konduktancją i oznaczamy literą G.
Jednostką konduktancji jest siemens (S).
8
17
Cewka indukcyjna
Cewka indukcyjna (cewka) jest elementem pasywnym.
Posiada on tylko jedną cechę (parametr) go opisującą – indukcyjność. Parametr ten
oznaczamy literą L.
Jednostką indukcyjności jest Henr (H).
9
17
Kondensator
Kondensator jest elementem pasywnym.
Posiada on tylko jedną cechę (parametr) go opisującą – pojemność. Parametr ten
oznaczamy literą C.
Jednostką indukcyjności jest Farad (F).
10
17
Wykresy wektorowe
11
3
5
17
Metoda symboliczna analizy obwodów RLC
12
3
5
17
Rozwiązanie w stanie ustalonym
Składową ustaloną prądu w obwodzie można otrzymać nie rozwiązując równania różniczkowego opisującego ten obwód a korzystając jedynie z
metody liczb zespolonych (metody symbolicznej). Istotnym elementem tej metody jest zastąpienie przebiegów czasowych ich reprezentacją
zespoloną. Przyjmijmy, że prąd i(t) = Im sin(ωt + ψ) oraz napięcie u(t) = Um sin(ωt + ψ) zastąpione zostały przez wektory wirujące w czasie,
odpowiednio I(t) oraz U(t) określone w postaci:
i(t) = Im ejψ ejωt
u(t) = Um ejψ ejωt
Po zastąpieniu wartości czasowych prądu i napięcia poprzez ich reprezentację w postaci wektorów wirujących otrzymuje się:
U(t) = R·I(t) + L (dI(t)/dt) + (1/C) ∫I(t) dt
13
17
Rozwiązanie w stanie ustalonym
14
17
Impedancje zespolone
Impedancja (Z) jest to wielkość charakteryzująca zależność
między prądem i napięciem w obwodach prądu zmiennego.
W obwodach prądu zmiennego jest tym samym co opór
elektryczny w obwodach prądu stałego.
15
3
5
17
Trójkąt napięć oraz impedancji,
przesunięcie fazowe
16
17
Prawa Kirchhoffa dla wartości
skutecznych zespolonych
Prawo prądowe Kirchhoffa
Suma algebraiczna prądów zespolonych w dowolnym węźle obwodu
elektrycznego jest równa zeru, co zapiszemy w postaci: Σk Ik = 0.
Prawo napięciowe Kirchhoffa
Suma algebraiczna napięć zespolonych w każdym oczku obwodu elektrycznego
jest równa zeru, co zapiszemy w postaci: Σk Uk = 0
W równaniu tym symbolem Uk oznaczono wszystkie napięcia w postaci
zespolonej, zarówno na gałęziach pasywnych jak i źródłowych obwodu. Sposób
sumowania (znak plus lub minus) zarówno prądów jak i napięć jest taki sam jak
w przypadku operowania wartościami rzeczywistymi.
17
17