ATOM
1897r. – odkrycie przez J.J. Thomsona elektronu,
1911r. – odkrycie przez E. Rutherforda jądra atomu,
1913r. – przedstawienie przez N. Bohra modelu budowy atomów wodoropodobnych.
1897r. – odkrycie przez J.J. Thomsona elektronu,
1911r. – odkrycie przez E. Rutherforda jądra atomu,
1913r. – przedstawienie przez N. Bohra modelu budowy atomów wodoropodobnych.
Po odkryciu w 1911r. Jądra atomowego, E. Rutherford przedstawia jądrowy model
atomu. Jest to model, przypominający układ planetarny. W środku dodatnie jądro
(Słońce) a wokół poruszające się ujemne elektrony (planety).
1897r. – odkrycie przez J.J. Thomsona elektronu,
1911r. – odkrycie przez E. Rutherforda jądra atomu,
1913r. – przedstawienie przez N. Bohra modelu budowy atomów wodoropodobnych.
Po odkryciu w 1911r. Jądra atomowego, E. Rutherford przedstawia jądrowy model
atomu. Jest to model, przypominający układ planetarny. W środku dodatnie jądro
(Słońce) a wokół poruszające się ujemne elektrony (planety).
Oszacowano, że rozmiary jądra są rzędu 10-15m a rozmiary atomu 10-10m. Z tego
wynika, że gdyby jądro było kulką o średnicy 1cm, to elektron krążyłby w odległości od
niego ok. 100m (10 000 razy większej) – materia jest przeraźliwie pusta.
1897r. – odkrycie przez J.J. Thomsona elektronu,
1911r. – odkrycie przez E. Rutherforda jądra atomu,
1913r. – przedstawienie przez N. Bohra modelu budowy atomów wodoropodobnych.
Po odkryciu w 1911r. Jądra atomowego, E. Rutherford przedstawia jądrowy model
atomu. Jest to model, przypominający układ planetarny. W środku dodatnie jądro
(Słońce) a wokół poruszające się ujemne elektrony (planety).
Oszacowano, że rozmiary jądra są rzędu 10-15m a rozmiary atomu 10-10m. Z tego
wynika, że gdyby jądro było kulką o średnicy 1cm, to elektron krążyłby w odległości od
niego ok. 100m (10 000 razy większej) – materia jest przeraźliwie pusta.
Okazało się, że w świecie atomu zachodzą zjawiska, których nie można wytłumaczyć
w oparciu o prawa mechaniki klasycznej. Od tych odkryć rozpoczyna się burzliwy
rozwój fizyki atomowej, prowadzący do powstania teorii kwantów (mechaniki
kwantowej) opisujących świat atomowy.
Model atomu wodoru wg N. Bohra
Model atomu wodoru wg N. Bohra
Początki mechaniki kwantowej znajdujemy u N. Bohra, który przedstawia
matematyczny opis atomu wodoru. Jego model jest pomieszaniem klasycznego
spojrzenia na atom z uwzględnieniem pewnych faktów wynikających z badań atomu, a
których nie tłumaczy mechanika klasyczna.
Model atomu wodoru wg N. Bohra
Początki mechaniki kwantowej znajdujemy u N. Bohra, który przedstawia
matematyczny opis atomu wodoru. Jego model jest pomieszaniem klasycznego
spojrzenia na atom z uwzględnieniem pewnych faktów wynikających z badań atomu, a
których nie tłumaczy mechanika klasyczna.
Model ten dzisiaj, w dobie rozwiniętej mechaniki kwantowej, nie ma większego
znaczenia. Przedstawimy go, ponieważ w przystępny sposób wyjaśnia np.
promieniowanie atomów. Wzory końcowe, wyprowadzone przez N. Bohra, są takie
same jak wynikające z mechaniki kwantowej. Po odkryciu wielu nowych zjawisk w
świecie atomowym, model ten stał się mało użyteczny – nie objaśniał ich.
Postulaty Bohra:
1.Ruch elektronu wokół jądra odbywa się pod wpływem siły kulombowskiego
przyciągania po tzw. orbitach dozwolonych, dla których moment pędu elektronu
przyjmuje wartości:
gdzie: rn - to promień n-tej orbity,
vn - to prędkość elektronu na n-tej orbicie,
n = 1, 2, 3,… - to liczba kwantowa.
Postulaty Bohra:
1.Ruch elektronu wokół jądra odbywa się pod wpływem siły kulombowskiego
przyciągania po tzw. orbitach dozwolonych, dla których moment pędu elektronu
przyjmuje wartości:
gdzie: rn - to promień n-tej orbity,
vn - to prędkość elektronu na n-tej orbicie,
n = 1, 2, 3,… - to liczba kwantowa.
2.Przy przejściu elektronu z jednej orbity na inną elektron promieniuje energię:
DE = hn,
gdzie:
- stała Plancka,
n - częstotliwość promieniowania.
Postulaty Bohra:
1.Ruch elektronu wokół jądra odbywa się pod wpływem siły kulombowskiego
przyciągania po tzw. orbitach dozwolonych, dla których moment pędu elektronu
przyjmuje wartości:
gdzie: rn - to promień n-tej orbity,
vn - to prędkość elektronu na n-tej orbicie,
n = 1, 2, 3,… - to liczba kwantowa.
2.Przy przejściu elektronu z jednej orbity na inną elektron promieniuje energię:
DE = hn,
gdzie:
- stała Plancka,
n - częstotliwość promieniowania.
Mówimy, że moment pędu i energia są skwantowane, tzn. przyjmują tylko ściśle
określone wartości bez wartości pośrednich między nimi.
p
rn
+
Fc
-m
m – masa elektronu,
rn – promień n-tej orbity,
p – pęd elektronu,
Fc – siła Kulomba.
p
rn
+
-m
Fc
m – masa elektronu,
rn – promień n-tej orbity,
p – pęd elektronu,
Fc – siła Kulomba.
Siła elektrostatycznego przyciągania elektronu przez proton (siła Coulomba) jest siłą dośrodkową:
1 e 2 mv 2n
4o rn2
rn
p
rn
+
-m
Fc
m – masa elektronu,
rn – promień n-tej orbity,
p – pęd elektronu,
Fc – siła Kulomba.
Siła elektrostatycznego przyciągania elektronu przez proton (siła Coulomba) jest siłą dośrodkową:
1 e 2 mv 2n
4o rn2
rn
Energia całkowita układu elektron-proton jest sumą energii kinetycznej elektronu i ich elektrycznej energii
potencjalnej:
2
2
En
mv n
1 e
2
4
r
o n
p
rn
+
-m
Fc
m – masa elektronu,
rn – promień n-tej orbity,
p – pęd elektronu,
Fc – siła Kulomba.
Siła elektrostatycznego przyciągania elektronu przez proton (siła Coulomba) jest siłą dośrodkową:
1 e 2 mv 2n
4o rn2
rn
Energia całkowita układu elektron-proton jest sumą energii kinetycznej elektronu i ich elektrycznej energii
potencjalnej:
2
2
En
Pierwszy postulat Bohra:
mv n
1 e
2
4
r
o n
mv n rn n
h
2
p
rn
+
-m
Fc
m – masa elektronu,
rn – promień n-tej orbity,
p – pęd elektronu,
Fc – siła Kulomba.
Siła elektrostatycznego przyciągania elektronu przez proton (siła Coulomba) jest siłą dośrodkową:
1 e 2 mv 2n
4o rn2
rn
Energia całkowita układu elektron-proton jest sumą energii kinetycznej elektronu i ich elektrycznej energii
potencjalnej:
2
2
En
Pierwszy postulat Bohra:
Drugi postulat Bohra:
mv n
1 e
2
4
r
o n
mv n rn n
h
2
DEmn = En- Em = hn.
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
4)
Dysponujemy układem czterech równań:
Wyznaczając z równania 3) v n
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
4)
nh
5)
2mrn
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
mamy:
4)
o h 2
rn n
6)
me 2
2
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
mamy:
4)
o h 2
rn n
6)
me 2
2
Z ostatniego równania wynika, że również promień n-tej orbity w atomie
wodoru jest skwantowany.
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
mamy:
4)
o h 2
rn n
6)
me 2
2
Z ostatniego równania wynika, że również promień n-tej orbity w atomie
wodoru jest skwantowany.
Dla n=1otrzymujemy wzór na promień pierwszej orbity w atomie wodoru:
o h 2
r1
0,53 1010 m
2
me
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
mamy:
4)
o h 2
rn n
6)
me 2
2
Z ostatniego równania wynika, że również promień n-tej orbity w atomie
wodoru jest skwantowany.
Dla n=1otrzymujemy wzór na promień pierwszej orbity w atomie wodoru:
o h 2
r1
0,53 1010 m
2
me
Dokonując podstawienia 5) i 6) do 2) znajdujemy:
1 me 4
En 2 2 2
n 8 o h
7)
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
mamy:
4)
o h 2
rn n
6)
me 2
2
Z ostatniego równania wynika, że również promień n-tej orbity w atomie
wodoru jest skwantowany.
Dla n=1otrzymujemy wzór na promień pierwszej orbity w atomie wodoru:
o h 2
r1
0,53 1010 m
2
me
Dokonując podstawienia 5) i 6) do 2) znajdujemy:
1 me 4
En 2 2 2
n 8 o h
Z ostatniego równania wynika, że również energia atomu wodoru w stanie n-tym jest skwantowana.
7)
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
mamy:
4)
o h 2
rn n
6)
me 2
2
Z ostatniego równania wynika, że również promień n-tej orbity w atomie
wodoru jest skwantowany.
Dla n=1otrzymujemy wzór na promień pierwszej orbity w atomie wodoru:
o h 2
r1
0,53 1010 m
2
me
Dokonując podstawienia 5) i 6) do 2) znajdujemy:
1 me 4
En 2 2 2
n 8 o h
7)
Z ostatniego równania wynika, że również energia atomu wodoru w stanie n-tym jest skwantowana.
me 4
Dla n=1otrzymujemy wzór na najmniejszą możliwą energię tzw. stanu podstawowego: E1 2 2 13,6eV.
8 o h
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
mamy:
4)
o h 2
rn n
6)
me 2
2
Z ostatniego równania wynika, że również promień n-tej orbity w atomie
wodoru jest skwantowany.
Dla n=1otrzymujemy wzór na promień pierwszej orbity w atomie wodoru:
o h 2
r1
0,53 1010 m
2
me
Dokonując podstawienia 5) i 6) do 2) znajdujemy:
1 me 4
En 2 2 2
n 8 o h
7)
Z ostatniego równania wynika, że również energia atomu wodoru w stanie n-tym jest skwantowana.
me 4
Dla n=1otrzymujemy wzór na najmniejszą możliwą energię tzw. stanu podstawowego: E1 2 2 13,6eV.
8 o h
Dla rosnących n energia atomu wodoru rośnie (zbliża się do zera). Dla n energia ta jest największa i wynosi
E 0. Następuje wtedy jonizacja atomu.
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
mamy:
4)
o h 2
rn n
6)
me 2
2
Z ostatniego równania wynika, że również promień n-tej orbity w atomie
wodoru jest skwantowany.
Dla n=1otrzymujemy wzór na promień pierwszej orbity w atomie wodoru:
o h 2
r1
0,53 1010 m
2
me
Dokonując podstawienia 5) i 6) do 2) znajdujemy:
1 me 4
En 2 2 2
n 8 o h
7)
Z ostatniego równania wynika, że również energia atomu wodoru w stanie n-tym jest skwantowana.
me 4
Dla n=1otrzymujemy wzór na najmniejszą możliwą energię tzw. stanu podstawowego: E1 2 2 13,6eV.
8 o h
Dla rosnących n energia atomu wodoru rośnie (zbliża się do zera). Dla n energia ta jest największa i wynosi
E 0. Następuje wtedy jonizacja atomu.
Z równań 4) i 7) otrzymujemy wzór na energię absorbowaną przez atom co wiąże się z przeskokiem elektronu na
orbitę dalszą. Jest to jednocześnie energia fotonu emitowanego przez atom, gdy elektron spada na orbitę bliższą
jądra:
Dysponujemy układem czterech równań:
1 e 2 mv 2n
4o rn2
rn
1)
mv 2n
1 e2
En
2
4
r
o n
2)
h
2
3)
mv n rn n
DEmn = En- Em = hn.
nh
5) i wstawiając tę zależność do 1)
2mrn
Wyznaczając z równania 3) v n
o h 2
rn n
6)
me 2
mamy:
4)
2
Z ostatniego równania wynika, że również promień n-tej orbity w atomie
wodoru jest skwantowany.
Dla n=1otrzymujemy wzór na promień pierwszej orbity w atomie wodoru:
o h 2
r1
0,53 1010 m
2
me
Dokonując podstawienia 5) i 6) do 2) znajdujemy:
1 me 4
En 2 2 2
n 8 o h
7)
Z ostatniego równania wynika, że również energia atomu wodoru w stanie n-tym jest skwantowana.
me 4
Dla n=1otrzymujemy wzór na najmniejszą możliwą energię tzw. stanu podstawowego: E1 2 2 13,6eV.
8 o h
Dla rosnących n energia atomu wodoru rośnie (zbliża się do zera). Dla n energia ta jest największa i wynosi
E 0. Następuje wtedy jonizacja atomu.
Z równań 4) i 7) otrzymujemy wzór na energię absorbowaną przez atom co wiąże się z przeskokiem elektronu na
orbitę dalszą. Jest to jednocześnie energia fotonu emitowanego przez atom, gdy elektron spada na orbitę bliższą
jądra:
DE mn
me 4 1
1
2 3 2 2
8 o h m n
WIDMO EMISYJNE WODORU
WIDMO EMISYJNE WODORU
W stanie naturalnym większość atomów znajduje się w stanie podstawowym (elektron na pierwszej orbicie, n=1).Przejście elektronu na orbitę
wyższą energetycznie (n=2,3,4,…), czyli wzbudzenie atomu może
nastąpić za pomocą:
- wysokiej temperatury,
- wysokiego napięcia.
WIDMO EMISYJNE WODORU
W stanie naturalnym większość atomów znajduje się w stanie podstawowym (elektron na pierwszej orbicie, n=1).Przejście elektronu na orbitę
wyższą energetycznie (n=2,3,4,…), czyli wzbudzenie atomu może
nastąpić za pomocą:
- wysokiej temperatury,
- wysokiego napięcia.
Większość wzbudzanych w ten sposób atomów różnych pierwiastków
przebywa w stanie wzbudzonym przez określony czas.
Średni czas życia atomu w stanie wzbudzonym jest
t = 10-8s.
WIDMO EMISYJNE WODORU
W stanie naturalnym większość atomów znajduje się w stanie podstawowym (elektron na pierwszej orbicie, n=1).Przejście elektronu na orbitę
wyższą energetycznie (n=2,3,4,…), czyli wzbudzenie atomu może
nastąpić za pomocą:
- wysokiej temperatury,
- wysokiego napięcia.
Większość wzbudzanych w ten sposób atomów różnych pierwiastków
przebywa w stanie wzbudzonym przez określony czas.
Średni czas życia atomu w stanie wzbudzonym jest
t = 10-8s.
Po tym czasie odbywa się spontaniczne (emisja spontaniczna) przejście
elektronu na orbity niższe energetycznie. Związane jest to z emisją
fotonów o ściśle określonych energiach odpowiadających tym
przejściom.
n=6
n=5
n=4
n=3
n=2
Seria
Pfunda
(podczerwień)
Seria
Paschena
(podczerwień)
Seria
Balmera
(widzialna)
stany wzbudzone
WIDMO EMISYJNE WODORU
W stanie naturalnym większość atomów znajduje się w stanie podstawowym (elektron na pierwszej orbicie, n=1).Przejście elektronu na orbitę
wyższą energetycznie (n=2,3,4,…), czyli wzbudzenie atomu może
nastąpić za pomocą:
- wysokiej temperatury,
- wysokiego napięcia.
Większość wzbudzanych w ten sposób atomów różnych pierwiastków
przebywa w stanie wzbudzonym przez określony czas.
Średni czas życia atomu w stanie wzbudzonym jest
t = 10-8s.
Po tym czasie odbywa się spontaniczne (emisja spontaniczna) przejście
elektronu na orbity niższe energetycznie. Związane jest to z emisją
fotonów o ściśle określonych energiach odpowiadających tym
przejściom.
n=1
Seria
Lymanna
(ultrafiolet)
stan podstawowy
Światło wysyłane przez pobudzony do świecenia wodór, rozszczepione
w pryzmacie ma widmo liniowe, składające się z prążków
odpowiadających kwantom energii emitowanej podczas poszczególnych
przejść elektronów. Linie w widmie wodoru układają się w serie
nazwane imionami ich odkrywców. Serie powstają podczas przeskoków
elektronów z orbit dalszych na określoną.
n=6
n=5
n=4
n=3
n=2
Seria
Pfunda
(podczerwień)
Seria
Paschena
(podczerwień)
Seria
Balmera
(widzialna)
stany wzbudzone
WIDMO EMISYJNE WODORU
W stanie naturalnym większość atomów znajduje się w stanie podstawowym (elektron na pierwszej orbicie, n=1).Przejście elektronu na orbitę
wyższą energetycznie (n=2,3,4,…), czyli wzbudzenie atomu może
nastąpić za pomocą:
- wysokiej temperatury,
- wysokiego napięcia.
Większość wzbudzanych w ten sposób atomów różnych pierwiastków
przebywa w stanie wzbudzonym przez określony czas.
Średni czas życia atomu w stanie wzbudzonym jest
t = 10-8s.
Po tym czasie odbywa się spontaniczne (emisja spontaniczna) przejście
elektronu na orbity niższe energetycznie. Związane jest to z emisją
fotonów o ściśle określonych energiach odpowiadających tym
przejściom.
n=1
Seria
Lymanna
(ultrafiolet)
stan podstawowy
Światło wysyłane przez pobudzony do świecenia wodór, rozszczepione
w pryzmacie ma widmo liniowe, składające się z prążków
odpowiadających kwantom energii emitowanej podczas poszczególnych
przejść elektronów. Linie w widmie wodoru układają się w serie
nazwane imionami ich odkrywców. Serie powstają podczas przeskoków
elektronów z orbit dalszych na określoną.
Jeśli atomy dowolnych pierwiastków są swobodne (stan gazu lub pary)
to dają widma emisyjne liniowe.
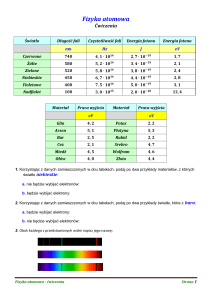
PRZYKŁADY WIDM
Ciągłe. Daje je żarówka
żarnikowa i Słońce.
l = <0,36mm – 0,72mm>
Emisyjne liniowe.
Dają je pary i gazy.
Absorpcyjne.
Odwrócenie widma
emisyjnego.
Liniowo-pasmowe
atomów żelaza
Widma pasmowe emitują cząsteczki. Każde pasmo zawiera wiele linii blisko siebie położonych.
PRZYKŁADY WIDM
Słońce – linie absorpcyjne na tle widma ciągłego
Wodór
Widmo absorpcyjne powstaje wtedy, gdy z widma ciągłego,
przechodzącego przez gazy lub pary zostają pochłonięte przez
nie długości fal odpowiadające wzbudzeniom ich atomów.
Hel
Rtęć
Uran