prezentacja

INŻYNIERIA MATERIAŁÓW O
SPECJALNYCH WŁASNOŚCIACH
Przyrost temperatury podczas
odkształcenia
Przyrost temperatury podczas odkształcenia
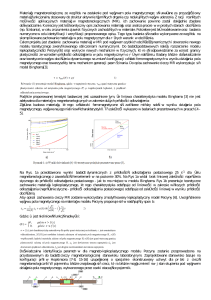
Odkształcanie z dużymi prędkościami prowadzi do zmiany warunków z izotermicznych na
adiabatyczne, a energia cieplna związana z pracą odkształcenia plastycznego widoczna jest we
wzroście temperatury odkształcanego ciała. Odkształcanie plastyczne generuje pracę, która jest
zamieniana na ciepło. Wynikający z tego wzrost temperatury może wywołać zmianę własności
materiału, np. tzw. „cieplne mięknięcie”. Równanie przewodzenia ciepła, które wiąże stan
mechaniczny (odkształcenia i naprężenia) z temperaturą ma postać:
kET0 t r e 

c p  T  c pT   p 
1  2
2
gdzie:
α – współczynnik przewodzenia ciepła
ρ – gęstość
cp – ciepło właściwe
 – szybkość zmiany energii odkształcania na energię cieplną
 – intensywność naprężenia
 p – prędkość odkształcenia plastycznego
k – współczynnik wydzielania ciepła
E – moduł Younga
T0 – temperatura początkowa lub otoczenia
e – prędkość odkształcenia sprężystego
 – współczynnik Poissona
(1)
Przyrost temperatury podczas odkształcenia
Pierwszy składnik po prawej stronie równania (1) przedstawia wzrost temperatury z
powodu nieodwracalnego odkształcenia plastycznego, drugi – nagrzewanie z powodu
odwracalnego efektu cieplno – sprężystego. Jeśli pominiemy sprężystość i fakt, że
przeważają warunki adiabatyczne, wówczas równanie ciepła przyjmuje bardziej prostą
postać. Szybkość przekształcenia pracy odkształcenia plastycznego na ciepło można
przedstawić za pomocą następującej zależności:

c pT
(2)
 p
Ogólnie można przyjąć, że w literaturze występują dwa podstawowe modele dla opisu
przyrostu temperatury w efekcie ciepła odkształcenia. Pierwszy z nich zakłada, że
współczynnik  przelicza jednostkowe zużycie pracy na jednostkowe zużycie ciepła. Dla
większości materiałów  = 0.9. W ten sposób wzrost temperatury podczas odkształcania
można wyrazić jako:

T 
c p
f
0.9

d


0
c p
f
 d
0
(3)
Przyrost temperatury podczas odkształcenia
Inną , często stosowaną metodą dla obliczania przyrostu temperatury w warunkach bardzo
dużych prędkości odkształcenia jest wykorzystanie następującej zależności:
T 
gdzie:
E
Cp
(4)
E – energia odpowiadająca bieżącemu ciśnieniu
Cp – pojemność cieplna
Wytworzona energia jest efektem ciśnienia wywołanego obciążeniem szokowym i
związaną z tym zmianą gęstości (p0 = 0 przy ciśnieniu wynoszącym 0):
 1
1
1 

E   p p  p0 



2
 0 p 
gdzie:
pp – ciśnienie przy obciążeniu udarowym
p0 – ciśnienie „zerowe”
 0 – gęstość przy zerowym ciśnieniu
 p – gęstość przy ciśnieniu udarowym
(5)
Przyrost temperatury podczas odkształcenia
Wpływ
wielkości
ziarna
austenitu na naprężenie
plastycznego płynięcia:
Rola mikrododatków
stopowych to w tym
przypadku obniżanie energii
błędu ułożenia i zwiększanie
podatności do
bliźniakowania.
Efekt: różnice w krzywych
plastycznego płynięcia.
a)
b)
c)
d)
Przyrost temperatury podczas odkształcenia
Wyniki symulacji komputerowych MES – ściskanie w temp. pokojowej próbek cylindrycznych
Wpływ rozdrobnienia struktury
Prędkość odkształcenia 1800s-1
Model KHL; Odkształcenie=0.5; Prędkość odkształcenia=1000s-1, T=293K
dα =100 μm
dα =500 nm
dα =100 nm
12 μm
4 μm
2 μm
Przyrost temperatury podczas odkształcenia
Wyniki symulacji komputerowych MES – ściskanie w temp. pokojowej próbek cylindrycznych
Wpływ wielkości odkształcenia i składu chemicznego
Przyrost temperatury podczas odkształcenia
ZADANIE 1:
Próbki wykonane ze stali mikrostopowej odkształcono w próbie osiowosymetrycznego
ściskania w różnych temperaturach w warunkach obciążenia dynamicznego (2500 s-1 ).
Zadano odkształcenia równe 0,1 i 0,2. Odczytać wartości naprężenia dla danych
odkształceń i wyznaczyć przyrost temperatury w próbkach. Przyjąć gęstość stali
7890kg/m3 oraz ciepło właściwe 452 J/kgK.
CEL: wpływ temperatury odkształcania na przyrost temperatury
ZADANIE 2:
Próbki wykonane ze stali odkształcono w próbie osiowosymetrycznego ściskania na
zimno, w warunkach obciążenia quasi-statycznego (0,001 s-1) i dynamicznego (3000 s-1 ).
Zadano odkształcenia równe 0,2; 0,4 i 0,6. Odczytać wartości naprężenia dla danych
odkształceń i wyznaczyć przyrost temperatury w próbkach. Przyjąć gęstość stali
7890km/m3 oraz ciepło właściwe 452 J/kgK.
CEL: wpływ warunków odkształcania na przyrost temperatury
Wyznaczanie naprężenia uplastyczniającego w warunkach
odkształceń dynamicznych
Johnson – Cook:
Zerilli-Armstrong:
n=0.298
Wyznaczanie naprężenia uplastyczniającego w warunkach
odkształceń dynamicznych
ZADANIE 3:
Wyznaczyć naprężenie uplastyczniające dla stali mikrostopowej o podwyższonej
wytrzymałości odkształcanej w warunkach quasi-statycznych i dynamicznych według
wzoru Johnson’a-Cook’a.
Temperatura odkształcania: 900 i 600°C
Prędkość odkształcenia: 1 i 2500 1/s
Odkształcenie: 0.2
ZADANIE 4:
Próbki wykonane ze stali odkształcono w próbie osiowosymetrycznego ściskania w
warunkach obciążenia quasi-statycznego (1 s-1) i dynamicznego (2500 s-1 ). Wyznaczyć
wartości naprężenia uplastyczniającego z wykorzystaniem zależności Z-A.
Temperatura odkształcania: 900 i 600°C
Prędkość odkształcenia: 1 i 2500 1/s
Odkształcenie: 0.2
Wlk. ziarna austenitu i ferrytu odpowiednio: 25 i 5 mikrometrów.
CEL: wpływ temperatury odkształcania i prędkości na naprężenie uplastyczniające.