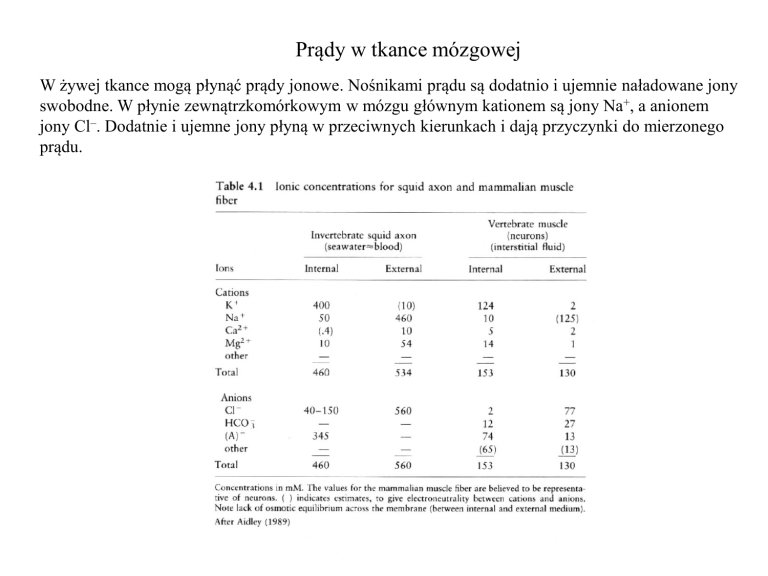
Prądy w tkance mózgowej
W żywej tkance mogą płynąć prądy jonowe. Nośnikami prądu są dodatnio i ujemnie naładowane jony
swobodne. W płynie zewnątrzkomórkowym w mózgu głównym kationem są jony Na+, a anionem
jony Cl–. Dodatnie i ujemne jony płyną w przeciwnych kierunkach i dają przyczynki do mierzonego
prądu.
Gęstość prądu
W odróżnieniu od obwodów elektrycznych, w których prąd jest rozłożony równomiernie w całym
przekroju poprzecznym elementów obwodu i można operować pojęciem prądu całkowitego, w tkance
nerwowej wygodnie operuje się uogólnionym pojęciem tzw. gęstością prądu J. Gęstość prądu
pochodzącego do wielu różnych jonów, można wyrazić jako sumę poszczególnych przyczynków od
jonów mających gęstość ładunku ρi i prędkość vi:
Gęstość ładunku jest równa wartości ładunku danego jonu pomnożonej przez liczbę wolnych jonów
w elemencie objętości tkanki. Jednostką gęstości ładunku jest C/m3. vi są to średnie prędkości
jonów wyrażone w metrach na sekundę. Gęstość prądu jest to ilość prądu przepływająca przez
jednostkowy przekrój poprzeczny, a jego jednostką jest C/(m2s) lub A/m2.
Gęstość prądu
W jednorodnym przewodniku, o przekroju poprzecznym A, w którym płynie prąd I, gęstość prądu J
= I/A jest stała (w przestrzeni). DV = hlI/A, h = 1/s – opór właściwy.
W tkance mózgowej przepływ prądu jest niejednorodny. Gęstość prądu J(r,t) najczęściej nie jest
stała dla r na żadnym przekroju poprzecznym A.
Rozkład gęstości prądu w mózgu oszacowany
za pomocą rozwiązania problemu odwrotnego
zastosowanego do 256-kanałowego zapisu
EEG. Przestrzeń rozwiązań jest ograniczona do
materii szarej na podstawie obrazowania MRI.
Dodatkowo, opór właściwy (przewodnictwo) może zależeć od położenia r (ośrodek niejednorodny),
oraz od kierunku (ośrodek anizotropowy).
Prądy w tkance mózgowej
W skali makroskopowej (np. w próbce materii zawierającej 1020 lub więcej ładunków w ruchu),
tkanka nerwowa spełnia prawo Ohma (dla małych pól elektrycznych, takich jak w zagadnieniach
EEG). Oznacza to liniową zależność pomiędzy gęstością prądu J, a przyłożonym polem
elektrycznym E:
Stała proporcjonalności σ jest nazywana przewodnictwem elektrycznym ośrodka i wyraża się w
jednostkach 1/(Ωm) lub równoważnie w Siemens/m (S/m). W tkance biologicznej często
wygodniej jest stosować jednostki 1/(Ωcm) lub 1/(Ωmm) i (S/mm)
Prądy w tkance mózgowej
Dzięki dużemu oporowi błon komórkowych, prądy płynące w tkance mózgowej ‘omijają’
komórki i płyną w przestrzeni zewnątrzkomórkowej. Słabo przewodzące i gęsto ułożone
komórki zwiększają wypadkową oporność tkanki. Jednocześnie, dzięki omijaniu elementów
nieliniowych, tkankę można traktować jako ośrodek spełniający liniowe prawo Ohma. Na
poziomie mikroskopowym, błony komórkowe wykazują zachowanie nieliniowe, odbiegające
od prawa Ohma.
Zagadnienia związane z przepływem prądu w ośrodkach z jednorodnie rozmieszczonymi sferami
i walcami, o zadanym przewodnictwie, badali Maxwell (1891) i Rayleigh (1892).
Prądy w tkance mózgowej
Dla nieprzewodzących sfer i walców, stosunek oporności całego ośrodka h, do oporności płynu hS
wynosi:
h 1 h
hS 1
wzór Maxwella - Rayleigha
– względna objętość nieprzewodzących obiektów
h – czynnik zależny od geometrii. h = ½ dla sfer, h = 1 dla walców.
W tkance mózgowej neurony zajmują 40-50%, glej 35 – 56%. Przestrzeń zewnątrzkomórkowa
zajmuje 2 – 20%. Ze wzoru Maxwella – Rayleigha wynika, że gdy > 1, h dąży do
nieskończoności.
Oporność tkanki mózgowej
Tkanka mózgowa jest słabym przewodnikiem. Średnia oporność substancji szarej mózgu
(zawierającej ciała komórek) jest większa niż oporność substancji białej mózgu (zawierającej
aksony komórek). Przewodnictwo płynów fizjologicznych jest duże ze względu na zawartość
jonów Na i Cl.
Struktura czaszki
W przekroju głowy można wyróżnić
następujące struktury:
Skóra (skin)
Czaszka (skull )
Opony mózgowo-rdzeniowe (meninges):
– opona twarda (dura mater)
– opona pajęcza (arachnoid mater)
– opona miękka (pia mater)
W niektorych okolicach czaszki opony
pajecza i miękka oddalają się od siebie,
tworząc przestrzeń wypełnioną płynem
mózgowo-rdzeniowym.
Modele głowy
Trójsferyczny modelu głowy składa się ze sfery
wewnętrznej (mózg), otoczonej dwiema
sferami (czaszka i skóra).
Bardziej realistyczny model głowy składa się z
warstwy skóry, trzech warstw czaszki i warstwy
płynu mózgowo – rdzeniowego (CSF) płynącego
pomiędzy oponami. Strzałki pokazują
preferowane obszary przepływu prądu.
Oporność czaszki
Ładunki w tkance mózgowej
Tkanka nerwowa wykazuje własności dielektryczne i opornościowe. Gdy umieścimy w niej
próbny ładunek punktowy +q, pojawią się następujące efekty:
1.
Efekty polaryzacyjny, związany z ładunkami związanymi (nieswobodnymi) w błonach
komórkowych.
2.
Efekt opornościowy, związany z ładunkami swobodnymi. Jego efektem będzie osłabienie
pola ładunku próbnego.
a)
b)
Ekranowanie Debye pola ładunku punktowego poprzez pola
innych ładunków przewodnika. Wypadkowe pole jest sumą pól
od wszystkich ładunków.
Pole podwójnej naładowanej warstwy (np. błony komórkowej)
w przewodniku wynosi 0 dla odległości makroskopowych.
Ekranowanie Debye
Potencjał pochodzący od ładunku próbnego umieszczonego w elektrolicie:
RD jest tzw. długością Debye'a, κ odpowiada za efekty polaryzacyjne, R – odległość od
ładunku punktowego.
Dla κ = 1 i R ≪ RD, dostajemy potencjał ładunku punktowego w próżni.
Dla RD rzędu kilku angstremów (10–10 m) w tkance biologicznej, exp(-R/RD) wynosi ok.
10–4000000 w odległości R = 3 mm.
Wniosek: potencjał ładunku próbnego umieszczonego w tkance biologicznej jest
zaniedbywalnie mały dla wszystkich makroskopowych odległości. Nie można więc
powiedzieć, że potencjały w mózgu są spowodowane pewnym określonym rozkładem
ładunku. Są one spowodowane nie tylko określonym rozkładem ładunku ale również
wszystkimi ładunkami w ośrodku przewodzącym.
W tkance biologicznej, prądy w błonach neuronalnych, a nie ładunki, są generatorami
EEG.
Podstawowe równania
Wszystkie zjawiska elektryczne i magnetyczne w mózgu podlegają uniwersalnym prawom Maxwella:
gdzie: D — indukcja elektryczna , E — natężenie pola elektrycznego, B — indukcja
magnetyczna, H — natężenie pola magnetycznego, ρ — gęstość ładunku, J — gęstość prądu.
W wielu materiałach, również w tkance nerwowej, pola D i B zależą liniowo od E i H:
Gdzie: ε — przenikalność elektryczna, a μ — przenikalność magnetyczna ośrodka.
Podstawowe równania
Do opisu pól elektrycznych w tkance nerwowej stosuje się uproszczoną wersje równań Maxwella
oraz równań opisujących liniowe własności ośrodka. Podstawowe równania liniowej
elektrofizjologii można podsumować następująco:
Zasada zachowania ładunku (z 1 i 4 prawa Maxwella)
Prawo Gaussa
Prawo Ohma
Liniowość dielektryka
Definicja potencjału skalarnego
Przydatny wzór:
Efekty opornościowe i pojemnościowe (polaryzacyjne)
Z równań:
i
Dostajemy:
(*)
Rozważmy składową pola elektrycznego oscylującego z częstością f
i wyraźmy równanie (*) stosując prawo Ohma
i liniowe równanie dla dielektryka
Dwa wyrażenia w nawiasie odpowiadają za efekty opornościowe i pojemnościowe w ośrodku
materialnym, tzn. efekty związane z ładunkiem swobodnym i efekty związane z ładunkami
związanymi w błonie komórkowej. Oznacza to, że efekty pojemnościowe możemy zaniedbać gdy:
(**)
W tkance biologicznej, stosunek (**) dla f = 10 Hz, jest rzędu ~10-4
Warunki brzegowe w ośrodkach niejednorodnych
Różne obszary mózgu mają różne przewodnictwa, tak więc w praktycznych zagadnieniach
występują granice między ośrodkami. W skali makroskopowej, najbardziej oczywiste granice
między ośrodkami dotyczą granicy pomiędzy słabo przewodzącą czaszką i powietrzem
otaczającym głowę. W skali mikroskopowej mamy do czynienia z granicami tworzonymi przez
błonę komórkową z ośrodkiem zarówno zewnętrznym jak i wewnętrznym. Potencjał elektryczny
Φ(r, t) będzie miał różne rozwiązania Φi(r, t) w obszarach i o przewodnictwie σi
Gdy w obszarze i oraz j nie występują źródła, podstawowe równania elektrofizjologii redukują się
do:
(*)
(**)
w każdym z regionów.
Równanie (*) odnosi się do sytuacji, w której można zaniedbać
efekty pojemnościowe (np. błony komórkowej) i nosi nazwę
równania Laplace’a. Równanie to stosuje się do wszystkich
zagadnień w skali makroskopowej. Równanie (**) stosuje się w
obszarach, w których nie można zaniedbać efektów
pojemnościowych - do błon komórkowych i pól w skali mikro.
Warunki brzegowe w ośrodkach niejednorodnych
Zawsze dane będzie jedno równanie na nieznany potencjał Φi(r, t) lub Φj(r, t) w danym obszarze.
Równania (*) i (**) mają nieskończenie wiele rozwiązań. Aby rozwiązanie w każdym obszarze
było jednoznaczne należy zastosować warunki brzegowe na granicy ośrodków oznaczonych
symbolami m i n:
składowa normalna – współrzędna u
składowe styczne – współrzędna w1 i w2
Pierwszy z warunków określa fizyczne wymaganie by składowa normalna gęstości prądu była
ciągła na granicy ośrodków. Warunek ten wynika z zasady zachowania ładunku. Drugi warunek
brzegowy określa, że składowa styczna pola elektrycznego musi być ciągła na granicy ośrodków.
Warunek ten wynika z drugiego prawa Maxwella. Stosując pierwszy z warunków brzegowych do
granicy głowa (m)–powietrze (n) i przyjmując, że przewodnictwo powietrza wynosi zero,
dostajemy:
Oznacza to, że pole magnetyczne, elektryczne oraz ich potencjały pochodzące od źródeł w
mózgu, rozchodzą się w przestrzeni otaczającej głowę, lecz prąd jest ograniczony do jej wnętrza
(składowa normalna prądu wynosi zero).
Źródła prądowe w mózgu
Tzw. problem wprost w EEG polega na obliczeniu potencjału na czaszce na podstawie źródeł
prądowych. Równania Laplace’a w pełni opisują szukany potencjał jednakże potrzebna jest
modyfikacja. Wersja niezmodyfikowana wymaga znajomości potencjału i jego pochodnych
normalnych na granicy ośrodków, co jest skomplikowane w skali komórkowej. Ponieważ jednak
składowa normalna potencjału jest proporcjonalna do gęstości prądu w przewodniku, możemy
zastąpić warunki brzegowe na granicy ośrodków poprzez odpowiednie źródła prądowe.
Prądy błonowe pojawiają się w wyniku
aktywacji pojedynczej synapsy. Np. w
wyniku hamującej akcji synaptycznej,
powstaje lokalne źródło prądowe w
okolicy synapsy oraz zlew prądowy
rozproszony wzdłuż dalszych obszarów
błony tak, by spełnione było prawo
zachowania ładunku.
Źródła prądowe w mózgu
Zakładamy, że ośrodek jest czysto przewodzący i nie wykazuje efektów pojemnościowych. W
takim ośrodku, ładunek nie jest nigdzie gromadzony, gęstość ładunku jest stała, a równanie
zachowania ładunku można zapisać:
(*)
Korzystne okazuje się wprowadzenie pojęcia makroskopowej gęstości prądu źródeł Js, która
pozwala zapisać prawo Ohma następująco:
(**)
Oznacza to, że prąd całkowity w ośrodku przewodzącym składa się prądu ohmowego σE oraz
prądu źródłowego wypływającego z granicy między ośrodkami np. prąd wypływający przez
błonę komórkową. Wstawiając (**) do (*) i korzystając z definicji potencjału elektrycznego
dostajemy:
równanie Poissona
gdzie objętościowe źródło prądowe jest zdefiniowane jako:
Źródła prądowe w mózgu
Obszar przewodnika zaznaczony jest zaokrąglonym prostokątem. a) Obszary wewnętrzne
(okręgi) są wyłączone z przewodnika. Potencjał wewnątrz przewodnika jest określony
równaniem Laplace'a. Jednoznaczne rozwiązanie tego równania wymaga znajomości potencjału
lub pochodnej normalnej potencjału na powierzchniach granicznych przewodnika. b) Zamiast
podawać warunki brzegowe na granicach przewodnika, możemy podać źródła prądowe s(r, t)
występujące na tych powierzchniach. W tej sytuacji jednoznaczne rozwiązanie dla potencjału
wewnątrz przewodnika jest dane równaniem Poissona. Obszary zaznaczone kolorem szarym są
źródłami prądu, pozostałe (białe na rys. b) obszary są bezźródłowe.
Bezpośrednie zastosowanie makroskopowych źródeł prądu
Z równań:
Dostajemy równanie Poissona w dielektryku czyli równanie na potencjał w dielektryku
pochodzący od obszaru źródła z pewną gęstością swobodnego ładunku ρ(r, t).
Równanie to ma postać równania Poissona w przewodniku.
Oba równania są równaniami Poissona lecz ze zmienionymi symbolami. Są one więc
matematycznie równoważne lecz reprezentują inne fizycznie procesy.
Potencjał N punktowych źródeł prądowych
Swobodny ładunek makroskopowy w przewodniku w praktyce wynosi zero, tak więc równanie Poissona w
dielektryku nie ma praktycznego zastosowania w elektrofizjologii. Jednakże w fizyce znanych jest wiele
rozwiązań tego równania dla różnych rodzajów niejednorodności w dielektrykach. Aby zastosować znane z
fizyki rozwiązania do przewodnika wystarczy w nich podstawić przewodnictwo σ(r, t) w miejsce
przenikalności elektrycznej ε(r, t), a źródła ładunku ρ(r, t) zamienić na źródła prądowe s(r, t).
Np. rozważmy specjalny przypadek N punktowych źródeł prądowych, co oznacza, że rozmiary (objętość)
źródła jest dużo mniejsza niż odległość od elektrod pomiarowych. W nieskończonym, jednorodnym i czysto
opornościowym przewodniku, potencjał na zewnątrz źródeł jest analogiczny do potencjału pochodzącego od
N ładunków punktowych i wynosi:
W typowych jednostkach stosowanych w zagadnieniach EEG, In(t) są jednobiegunowymi źródłami
prądowymi (μA) wypływającymi z n-tego rejonu źródła do przewodnika o przewodnictwie σ
(1/(Ωcm)). Rn są odległościami pomiędzy miejscem pomiaru a położeniem źródła. Np. potencjał w
odległości 1 cm generowany przez źródło prądowe o natężeniu 4π μA w wyidealizowanej korze
mózgowej o oporności η = 1/σ = 300 Ωcm, wynosi 300 mV. W ośrodku czysto opornościowym,
zależność czasowa potencjału jest dana przez sumę ważoną wszystkich źródeł. W ośrodku z
własnościami pojemnościowymi wystąpią przesunięcia fazowe pomiędzy źródłami i potencjałem. Gdy
zaniedbamy efekty pojemnościowe, otrzymamy ogólną metodę znajdowania potencjału na podstawie
rozkładu źródeł prądowych w mózgu.
Źródło jednobiegunowe
W nieskończonym, jednorodnym i czysto opornościowym przewodniku, potencjał pojedynczego
źródła jednobiegunowego wynosi:
Dipol prądowy
W nieskończonym, jednorodnym i czysto opornościowym przewodniku, potencjał dipola prądowego
(punktowego źródła I i zlewu –I, oddzielonych o d) wynosi:
Dużo wygodniej wyrazić potencjał dipola za pomocą jednej współrzędnej radialnej r, mierzonej od
środka odcinka łączącego ładunki. W odległościach dużo większych od d, potencjał dipola można
przybliżyć następująco:
dla r ≫ d. Θ jest kątem pomiędzy osią dipola i wektorem r wskazującym punkt pomiaru.
Dipol prądowy
Znaczenie dipola w elektrofizjologii jest większe niż jakakolwiek inna konfiguracja źródeł. Jest tak
dlatego, że prawie każdy obszar zawierający źródło i zlew, oraz w którym całkowity prąd źródła i
zlewu są równe (zasada zachowania prądu), będzie dawał przybliżone pole dipola w odległościach
dużych w porównaniu z rozmiarami obszaru źródło-zlew. Np. Pobudzona synaptycznie komórka
wytwarza pole dipola w otaczającej przestrzeni.
Rozkład linii prądu (linia ciągłą) linii izopotencjału
(linia przerywana) w wyniku pobudzenia
synaptycznego dendrytu wierzchołkowego komórki.
Potencjał komórki, jest z dobrym przybliżeniem
potencjałem dipola.
Rozkład linii prądu (linia ciągła) i linii
izopotencjału (linia przerywana) dipola
elektrycznego .
Kwadrupol prądowy
Rozróżniamy dwie konfiguracje prowadzące do źródła kwadrupolowego. Kwadrupol liniowy składa
się z dwóch źródeł +I/2 i zlewu –I leżących wzdłuż jednej prostej, oddzielonych od siebie o d.
Kwadrupol dwuwymiarowy składa się z dwóch identycznych dipoli, umieszczonych równolegle do
siebie, o przeciwnej orientacji. Kwadrupol liniowy ma zastosowanie w elektrofizjologii gdyż
wykazuje podobieństwo do trójfazowego rozkładu źródeł we włóknie nerwowym podczas
potencjału czynnościowego. Potencjał kwadrupola w dowolnym miejscu ośrodka przewodzącego
wynika bezpośrednio ze wzoru na potencjał pojedynczego źródła jednobiegunowego
Kwadrupol liniowy
Rozkład źródeł we włóknie nerwowym podczas
generacji potencjału czynnościowego.
Warstwa dipolowa
Około 65 do 75% neuronów korowych u wszystkich gatunków ssaków jest ustawionych prostopadle
do powierzchni kory. Neurony korowe mają dużą liczbę wzajemnych połączeń powodujących
synchronizacje ich aktywności. Istnieją więc zarówno anatomiczne, jak i fizjologiczne podstawy by
uznać warstwę dipolową tworzoną przez równoległe, synchronicznie działające komórki, za
generator potencjałów korowych. Synchronizacja generatorów odgrywa tutaj kluczową rolę.
Rozważmy na początku dwa dipole, których prądy fluktuują z częstościami fA i fB. Może to
odpowiadać dwóm komórkom, dostającym zarówno wejścia pobudzające, jak i hamujące. Potencjał
mierzony przez elektrodę w punkcie P, wynosi:
IA oraz IB są maksymalnymi
wartościami prądu w każdym z
dipoli. Dodatkowo, zakładamy, że
cały prąd wypływający ze źródła
wpływa do zlewu w tym samym
dipolu, co jest spełnione gdy
odległość między dipolami L jest
znacznie większa niż odległość
pomiędzy efektywnymi biegunami d.
αA i αB są kątami fazowymi.
Warstwa dipolowa
Rozważmy wpływ wielu dipoli o podobnej sile (IA = IB = IC, itd) i podobnych częstościach (fA = fB =
fC, itd) na średni potencjał. Potencjał będzie oczywiście zależał od wszystkich odległości R1, R2, itd.,
możemy jednak sformułować pewne ogólne wnioski:
a. Gdy generatory są ze sobą w fazie (αA = αB = αC , itd), a dipole ustawione równolegle do siebie,
wyrażenia dodają się i dla m dipoli, uśredniony po czasie potencjał będzie proporcjonalny do
ilości wszystkich m generatorów w otoczeniu elektrody:
b. Jeśli generatory mają losową orientację, tak że prądy I będą miały losowe znaki lub jeśli losowe
będą fazy generatorów, potencjał będzie dużo słabiej zależał od liczby generatorów. Będzie on
wynikiem statystycznej fluktuacji. Można pokazać, że m członów w wyrażeniu sumuje się, dając
średni potencjał, który dla dużych m można oszacować jako:
Warstwa dipolowa
Potencjał mierzony przez elektrodę umieszczoną w pobliżu generatorów może być wyrażony
następującym przybliżonym wzorem:
Indeksy i, S, oraz A odnoszą się odpowiednio do źródeł lokalnych, źródeł odległych synchronicznych i
źródeł odległych asynchronicznych. d jest odległością pomiędzy efektywnymi biegunami dipoli. l, m i
n są liczbą źródeł lokalnych, odległych synchronicznych i odległych asynchronicznych, które znajdują
się odpowiednio w średnich odległościach Ri, RS, RA.
W przypadku elektrody EEG nie ma źródeł lokalnych. Jeśli generatory są podobne IS ≈ IA oraz
generatory synchroniczne i asynchroniczne są w podobnej odległości RS ≈ RA, względny przyczynek od
generatorów synchronicznych względem asynchronicznych wynosi:
Warstwa dipolowa
Elektroda umieszczona na czaszce mierzy aktywność ok. 108 neuronów znajdujących się w paru cm2
kory. Niech prawie wszystkie neurony są aktywne lecz tylko 1% (106) z nich jest ustawiony równolegle
i działa synchronicznie. Przyczynek od synchronicznej frakcji neuronów do potencjału mierzonego na
czaszce wynosi:
Jest on więc 100 razy większy niż przyczynek od pozostałych 99% neuronów. Pokazuje to, że
powierzchniowe EEG pochodzi głównie od synchronicznej aktywności równolegle ustawionych
neuronów, a zmiana amplitudy sygnału wraz ze stanem fizjologicznym, wiąże się ze zmianą liczby
synchronicznie działających komórek.
Warstwa ‘pionowych dipoli’
Warstwa ‘poziomych dipoli’
Pola otwarte i zamknięte
Warstwa dipoli o tej samej
orientacji tworzy pole
otwarte. Pola otwarte
występują w móżdżku, korze
i hipokampie.
Komórki ustawione
sferycznie symetrycznie
tworzą pola zamknięte.
Synchroniczna aktywacja
neuronów powoduje pole
mierzalne wewnątrz pola i
zerowe pole na zewnątrz
gdyż pola dipoli o
przeciwnej orientacji znoszą
się wzajemnie. Linią
przerywaną zaznaczono
granice zerowego potencjału.
Przestrzenny rozkład potencjału w korze
Doświadczalne zapisy rozkładu potencjału w korze motorycznej szczura. W zależności od
aktywności synaptycznej pionowy rozkład potencjału może zmieniać polaryzacje (na rysunku
zmiana zachodzi pomiędzy elektrodą 1 i 2), oraz postać oscylacji.
Analiza gęstości źródłowej prądu (current source density analysis - CSD)
Równanie Poissona:
Pomiary w punktach V0, Va, Vb
można przedstawić:
V
2
Js
s
Va Vm ( x Dx, t )
Vb Vm ( x Dx, t )
Gdzie:
Js
V0 Vm ( x, t )
- gęstość źródłowa prądu
V
- potencjał polowy
s
- przewodnictwo
Dla anatomicznie jednorodnych warstw, zmiana
potencjału wewnątrz warstwy wynosi 0, tzn.:
Pierwsza pochodna przestrzenna:
V (t ) Vb Va
x
2Dx
Druga pochodna przestrzenna:
2V 2V
0
y 2 z 2
Czyli:
V Js
x 2
s
2
nazywa się gęstością źródłową prądu.
Analiza gęstości źródłowej prądu - przykład
Analiza gęstości źródłowej prądu dostarcza
informacji na temat lokalizacji ‘zlewów’ i
‘źródeł’ prądów synaptycznych oraz prądów
aktywnych w komórce lub warstwie kory. Na
rysunku widoczne są: A. Potencjały polowe na
różnej głębokości generowane przez
stymulację kolaterali Schaffera w hipokampie.
B. Analiza gęstości źródłowej prądu.
Widoczne dwa maksima oznaczone ‘*’.
Maksimum (‘zlew’) w dendrytach pokazuje
lokalizacje wpływu prądu synaptycznego.
Maksimum (‘zlew’-’źródło’) w okolicy ciała
neuronu pokazuje miejsce generacji
potencjału czynnościowego