Grawitacja

POLE GRAWITACYJNE
Fakt odkrycia przez Newtona Prawa Grawitacji Powszechnej (nazywanej
też prawem Ciążenia Powszechnego) miał dla rozwoju ludzkości znacznie
większe znaczenie niż to sobie zazwyczaj wyobrażamy. Jest to spowodowane tym,
że
z prawa
grawitacji
wynika
ogromna
ilość
konsekwencji,
również
filozoficznych, a to w sposób nieuchronny doprowadza do nowego spojrzenia na
świat, przestrzeń, materię.
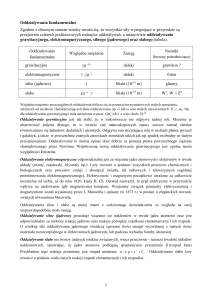
Grawitacja jest najsłabszym ze znanych oddziaływań – np., gdy weźmy dwa
najbardziej rozpowszechnione składniki materii: proton i elektron, to okaże się, że
siła przyciągania grawitacyjnego tych cząstek jest ponad 1039 razy mniejsza niż
siła przyciągania elektrostatycznego. Oznacza, to, że w większości przypadków,
gdy zaczynają działać siły typu elektrycznego, grawitacja przestaje się liczyć.
Grawitacja:
-
wiąże wszystkie masy we Wszechświecie,
-
jest najsłabszą wśród znanych nam sił,
-
działa na wszystkich odległościach,
-
jest zawsze przyciągająca.
Prawo powszechnego ciążenia
Porównując przyspieszenie grawitacyjne na orbicie Księżyca i na
powierzchni Ziemi, Newton zakładał, że Ziemia zachowuje się tak jakby jej cała
masa była skupiona w środku. Zgadywał, że tak ma być, ale dowód matematyczny
przeprowadził dopiero 20 lat później.
Doświadczenia związane z ruchami planet i spadaniem ciał na Ziemię,
ruchem pocisków, itp. dowodzą istnienia sił wzajemnego przyciągania się ciał. Siły
te podlegają prawu podanemu przez Newtona w 1687 roku, które głosi, że:
Między
dowolnymi
dwoma
punktami
materialnymi
działa
siła
wzajemnego przyciągania wprost proporcjonalna do iloczynu mas tych
punktów i odwrotnie proporcjonalna do kwadratu odległości miedzy nimi.
io
Prawo to nosi nazwę prawa powszechnego ciążenia, ponieważ dokładnie to
samo prawo stosuje się do wszystkich ciał i sił grawitacyjnych. Siły przyciągania
ciał podlegające temu prawu noszą natomiast nazwę sił grawitacyjnych. Wartość
siły grawitacyjnej jest określona następującym wzorem:
F12  G
m1 m 2
,
r122
gdzie współczynnik proporcjonalności G jest nazywany stałą grawitacji. W
zapisie wektorowym prawo grawitacji przyjmuje postać:


m 1m 2 r12
mm 
F12   G 2
 G 1 3 2 r12 ,
r12 r12
r12
z czego wynika, że siła grawitacyjna, jaką punkt materialny o masie m2 działa na
punkt materialny o masie m1 odległy od punktu m2 o
  
r12  r1  r2
jest skierowana wzdłuż prostej łączącej przyciągające się punkty materialne i jest
zwrócona przeciwnie do wektora promienia wodzącego punktu o masie m1
względem punktu o masie m2.
2
io
Stała grawitacji, G=(6,673+0,003)•10 m /kg•s , jest równa liczbowo sile
-11
3
2
grawitacyjnej, jaką wywierają na siebie dwa ciała o masie l kg każde z odległości
lm. Jest ona stałą uniwersalną.
Prawa Keplera
Praca Keplera (1609-1619) była wielkim odkryciem i aktem odwagi
zwłaszcza po tym jak w 1600 roku spalono na stosie Giordana Bruno zwolennika
systemu heliocentrycznego. Prawa Keplera wzmocniły hipotezę Kopernika.
Kepler
poszukiwał
nieskomplikowanej
geometrycznie
orbity,
żeby
udowodnić, że Mars i Ziemia muszą obracać się wokół Słońca. Po latach pracy
odkrył trzy proste prawa, które zgadzały się z wynikami pomiarowymi pozycji
planet z bardzo dużą dokładnością. Te prawa stosują się też do satelitów
okrążających jakąś planetę.
Pierwsze prawo Keplera
Każda planeta porusza się po elipsie, w której ognisku znajduje się Słońce.
Prawo to wynika z praw
ruchu ciała w polu siły
centralnej
i
odpowiada
przypadkowi
ujemnej
energii całkowitej.
Drugie prawo Keplera
Promień wodzący planety zakreśla w równych odstępach czasu równe pola.
3
io
Prawo to jest po prostu prawem
stałej prędkości polowej w ruchu
o stałym momencie pędu. Wynika
z niego
między innymi, że
prędkość planety jest największa
w punkcie przysłonecznym orbity,
a
najmniejsza
w
punkcie
odsłonecznym: Stałość prędkości
polowej

  L0
r v 
m
oznacza, bowiem, że prędkość
jest odwrotnie proporcjonalna do
promienia wodzącego.
Trzecie prawo Keplera
Kwadraty okresów obiegu planet dookoła Słońca są wprost proporcjonalne
do sześcianów większych półosi ich orbit.
Jeżeli przyjmie się upraszczające założenie, że orbita planety jest okręgiem
o promieniu R, to trzecie prawo Keplera można wyrazić wzorem:
T2
 const .
R3
Rozważmy ruch jakiejś planety o masie m po orbicie o promieniu R wokół Słońca.
Ruch ten jest ruchem jednostajnym po okręgu o okresie obiegu T. Siła dośrodkowa
działająca na tę planetę będzie siłą grawitacyjną. Określa ją w tym przypadku wzór:
ma d  G
mM
,
R2
42
M
,

G
2
3
T
R
4
io
stąd
4 2 T 2

 const .
GM R 3
III prawo Keplera dla planet poruszających się po orbitach kołowych.
Korzystając z wzoru na masę np. Słońca otrzymamy dla pierwszej planety:
4  2 R 13
M
GT12
a dla drugiej
4 2 R 32
M
GT22
Porównując otrzymuje się
R 13 R 32
 2
2
T1
T2
lub
R 13 T12

R 32 T22
.
Ciężar ciała
W pobliżu powierzchni Ziemi dla ciała o masie m będzie działała siła
ciężkości równa mg. Na Księżycu ciężar jest mniejszy w porównaniu z ciężarem
na Ziemi około sześć razy:
M Km
FK
R 2K
M K R 2Z


 0,165
FZ G M Zm M Z R 2K
R 2Z
G
Ważną konsekwencją tego, że siła grawitacyjna działająca na ciało jest
proporcjonalna do jego masy, jest możliwość pomiaru masy za pomocą pomiaru
siły grawitacyjnej. Można to zrobić używając wagi sprężynowej albo porównując
siły grawitacyjne działające na masę znaną (wzorzec) i na masę nieznaną.
5
io
Odgrywa tu rolę ta właściwość ciała, która powoduje jego przyciąganie przez inne
obiekty takie jak Ziemia i siła jest określona wzorem
FG
m' M Z
R 2Z
gdzie m' jest masą grawitacyjną.
Czy m i m' ciała są sobie równe?
Masa bezwładna m1 spadając swobodnie w pobliżu powierzchni Ziemi ma
przyspieszenie a1, przy czym
m 1a 1  G
m 1 'M Z
R 2Z
jeżeli inna masa m2 uzyskuje inne przyspieszenie a2 to
m 2a 2  G
m2 ' M Z
.
R 2Z
Dzieląc te równania przez siebie otrzymujemy
m 1a 1 m 1 '

.
m2a 2 m 2 '
Z tego równania wynika, że jeżeli wszystkie ciała spadają z tym samym
przyspieszeniem a1=a2=g, to iloraz mas bezwładnych jest równy ilorazowi mas
grawitacyjnych. Te wyniki sugerują, że masa bezwładna jest równa masie
grawitacyjnej. To stwierdzenie nazywa się zasadą równoważności.
Ruch ciała wywołany działaniem jego ciężaru nazywamy swobodnym
spadkiem. Przyspieszenie g nadane w tym ruchu ciału przez jego ciężar nazywa się
przyspieszeniem grawitacyjnym.
Dynamiczne równanie ruchu ciała spadającego swobodnie można zapisać
w postaci:
G
mM
 mg ,
R2
wówczas przyspieszenie:
gG
6
M
.
R2
io
Zależność powyższa prowadzi do bardzo ważnego wniosku:
przyspieszenie grawitacyjne danego ciała nie zależy od masy,
rozmiarów ani innych wielkości charakteryzujących to ciało.
Jest to właśnie przyczyną tego, że wszystkie ciała spadają w próżni
swobodnie z jednakowym przyspieszeniem.
Z wzoru tego wynika, że przyspieszenie grawitacyjne zależy od odległości
(wysokości) h ciała nad powierzchnię Ziemi. Wyrażając, bowiem odległość ciała od
środka Ziemi sumą promienia Ziemi R i wysokości h otrzymujemy zależność:
gh  G
M
,
(R  h) 2
lub
g Rh
2h

.
 1
gh  R 
R
2
Siła grawitacyjna, jaką Ziemia działa na każde ciało jest skierowana wzdłuż
promienia Ziemi i jest zwrócona ku jej środkowi. Wskutek ruchu obrotowego Ziemi
wokół własnej osi (ruch dobowy) na ciało znajdujące się na Ziemi działa również siła
odśrodkowa bezwładności.
7
io
Siłę wypadkową będącą sumą
geometryczną siły grawitacyjnej
i siły odśrodkowej bezwładności
związanej z ruchem dobowym Ziemi
nazywa się ciężarem ciała.
Ciężar Q jest, więc równy sile
grawitacyjnej
F,
tylko
na
biegunie.
Q bieg  G
Q równ
mM z
.
2
R
mM z
4 2
G
m 2 R
2
R
T
gdzie T jest okresem obrotu
Ziemi.
Pole grawitacyjne wewnątrz kuli
W przypadku powierzchni sferycznej o masie M i promieniu R, dla r>>R
natężenie pola grawitacyjnego jest równe
gG
M
R2
tj. tak jakby cała masa była skupiona w środku kuli.
Jakie jest jednak pole wewnątrz powierzchni sferycznej?
Dla powierzchni sferycznej o bardzo małej grubości dr można wybrać dwie
leżące naprzeciwko siebie powierzchnie A1 i A2. W dowolnym punkcie leżącym
wewnątrz sfery fragment A1 czaszy jest źródłem siły F1 
jest źródłem siły F2 
A2
.
r22
8
A1
, a powierzchnia A2
r12
io
Stąd
F1 A 1 r22

.
F2 A 2 r12
Z rozważań geometrycznych widać, że
A 1 r12

A 2 r22
(pola powierzchni stożków są proporcjonalne do kwadratu wymiarów liniowych).
Po podstawieniu do pierwszego równania:
F1
 1.
F2
Wynika stąd, że wkłady od A1 i A2 znoszą się. Można w ten sposób podzielić całą
powierzchnię sferyczną i uzyskać siłę wypadkową równą zero.
Tak, więc wewnątrz sfery siła oddziaływania grawitacyjnego jest równa zeru.
Pole wewnątrz sfery o dowolnej grubości też jest zero, ponieważ można podzielić
tą sferę na szereg cienkich warstw współśrodkowych.
9
io
Pole wewnątrz kuli o promieniu r:
g( r )  G
M( r )
.
r2
Jeżeli gęstość kuli jest stała to:

M (r ) M
M
 
V (r ) V 4  R 3
3
to
g( r )  G
M
r.
R3

Jest to zależność liniowa przyspieszenia grawitacyjnego od r .
10
io
Pole grawitacyjne
Chociaż pole jest pojęciem abstrakcyjnym to jest bardzo użyteczne
i znacznie upraszcza opis wielu zjawisk. Na przykład, w przypadku wielu mas,

można najpierw obliczyć (w punkcie r ) pole pochodzące od tych mas, a dopiero
potem siłę działającą na masę umieszczoną w tym punkcie.
Aby łatwiej można było opisać oddziaływania grawitacyjne wprowadza się pojęcia
pola grawitacyjnego. Oddziaływanie między dwoma punktami materialnymi zastępuje
się oddziaływaniem między polem i punktem materialnym. Pole to jest przy tym
wytworzone przez drugi punkt materialny. Według tej metody, gdy znane jest pole
grawitacyjne, znana też jest siła grawitacyjna działająca na masę punktową
umieszczoną w tym polu.
Pole grawitacyjne jest to przestrzeń, w której na umieszczone w niej ciała działa
siła grawitacyjna.

Miarą ilościową pola grawitacyjnego jest jego natężenie E . Wartość natężenia
pola grawitacyjnego jest równa liczbowo sile, jaką to pole działa na punkt materialny

o masie jednostkowej. Wektor natężenia E jest równoległy do siły grawitacyjnej. Jest
on przy tym tak samo zwrócony, jak wektor siły grawitacyjnej:


 
MR
E  g  G 3 .
R
Wektor R , odległości od masy M do danego punktu pola, w którym określamy
natężenie jest zwrócony od masy do punktu pola. Natężenie pola grawitacyjnego
i przyspieszenie grawitacyjne są określone tymi samymi wzorami.
Wzór ostatni pozwala wyciągnąć następujące wnioski:
-
Źródłem pola grawitacyjnego jest ciało o określonej masie,
-
Natężenie pola grawitacyjnego jest zwrócone ku masie, która to pole wytwarza,
-
Natężenie pola grawitacyjnego ma wymiar przyspieszenia.
Z polem sił wiąże się nie tylko przestrzenny rozkład wektora
natężenia pola, ale również przestrzenny rozkład energii.
11
io
Siły grawitacyjne należą do grupy sił zachowawczy. Fakt ten umożliwia
zdefiniowanie pewnej wielkości skalarnej pozwalającej opisywać ilościowo pole
grawitacyjne tak samo ściśle, jak jest to możliwe przy pomocy natężenia pola.
Wielkością tą jest potencjał pola grawitacyjnego, zwany też potencjałem
grawitacyjnym.
Potencjałem pola grawitacyjnego w danym punkcie A nazywamy stosunek
pracy, jaką wykonuje siła grawitacyjna przenosząc ciało próbne o masie m z punktu
A do punktu odniesienia C (pole grawitacyjne w tym punkcie jest równe zeru) do
wartości masy m:
VA 
WA  C
.
m
Ponieważ pole grawitacyjne znika dopiero w nieskończenie wielkiej odległości od
masy, która to pole wytworzyła, to pracę oblicza się najczęściej na drodze od punktu
A do nieskończoności. Potencjał grawitacyjny w punkcie znajdującym się w
odległości rA od źródła pola masy M jest określony zależnością:
 1
1 
1  Mm
VA   Fdr    G 2 dr  GM  
m rA
m rA
r
 r rA


M
  G .

rA

Jak wynika z ostatniego wzoru, potencjał pola grawitacyjnego jest wielkością
skalarną zależną od masy ciała wytwarzającego to pole. Znak „-" oznacza, że pole
grawitacyjne jest polem sił przyciągających.
Gdy dwa ciała o masach odpowiednio równych M i m znajdują się
w odległości
rA
od
siebie,
wówczas
ich
energia
potencjalna
związana
z oddziaływaniami grawitacyjnymi jest równa pracy, jaką musi wykonać siła
grawitacyjna, aby rozsunąć te ciała na odległość nieskończenie wielką:
E p  WrA  .
Ponieważ siła grawitacyjna jest siłą przyciągającą, przemieszczenie ciał i wektor siły
grawitacyjnej są przeciwnie zwrócone. Dlatego też grawitacyjna energia potencjalna
jest wielkością określoną wzorem:
 1
Mm
E p   Fdr    G 2 dr  GmM 
rA
rA
r
 r rA



12

mM
  G
.

r

A
io
Energia potencjalna ma wartość równo zeru w nieskończoności (punkt
odniesienia) i maleje w miarę zmniejszania się rA. Oznacza to, że siła jest
przyciągająca. Wzór ten jest prawdziwy bez względu na wybór drogi, po jakiej
punkt porusza się z nieskończoności do rA.
Pole
grawitacyjne
graficznie
przy
możemy
pomocy
przedstawić
pewnych
linii
i powierzchni związanych z wielkościami
charakteryzującymi to pole. Rodzinę linii
tworzą tak zwane linie sił pola grawitacyjnego.
Są to linie, do których w każdym ich punkcie
jest
styczny
wektor
natężenia
pola
grawitacyjnego.
Rodzinę powierzchni tworzą tak zwane powierzchnie ekwipotencjalne. Są to
powierzchnie, których wszystkie punkty mają taki sam potencjał grawitacyjny.
Powierzchnie ekwipotencjalne i linie sił przecinają się w każdym punkcie pola pod kątem
prostym. Linie sił zaczynają się w nieskończoności i kończą się na danej masie
punktowej wytwarzającej pole grawitacyjne. Biegną one radialnie. Powierzchnie
ekwipotencjalne są sferycznymi powierzchniami współśrodkowymi o środku
pokrywającym się z daną masą punktową.
Prędkości kosmiczne
Problemem, jaki występuje w kosmonautyce, polega na wprowadzenia statku
kosmicznego na orbitę okołoziemską. W tym celu należy nadać temu pojazdowi tak
dużą prędkość, by siła odśrodkowa bezwładności mogła zrównoważyć siłę
grawitacyjną przyciągania Ziemi. Gdy statek kosmiczny krąży wokół Ziemi
w niedalekiej odległości od powierzchni Ziemi, prędkość tę nazywa się pierwszą
prędkością kosmiczną.
Warunek równowagi statku kosmicznego w związanym z nim nieinercjalnym
układzie odniesienia:
13
io
Mm
v2
G 2 m ,
r
r
można wyznaczyć wartość prędkości, jaką powinien mieć statek kosmiczny na
orbicie okołoziemskiej. Prędkość ta jest równa:
vI 
GM
 gr ,
r
gdzie r jest odległością statku kosmicznego od środka Ziemi, natomiast g jest
przyspieszeniem grawitacyjnym w tej odległości.
Gdy statek kosmiczny porusza się w pobliżu Ziemi (r≈R), wtedy otrzymujemy
wyrażenie określające pierwszą prędkość kosmiczną. Podstawiając do ostatniego
wzoru dane liczbowe otrzymuje się wartość vI=7,91•103m/s.
Innym ważnym problemem kosmonautyki jest wyprowadzenie statku
kosmicznego poza obszar przyciągania Ziemi. Aby tego dokonać, trzeba temu
pojazdowi nadać większą prędkość w chwili startu niż w pierwszym przypadku, gdy
chodziło tylko o wprowadzenie go na orbitę okołoziemską.
Prędkość skierowaną wzdłuż promienia Ziemi i zwróconą od środka Ziemi
w nieskończoność o wartości odpowiadającej energii kinetycznej niezbędnej do
przeniesienia statku kosmicznego z powierzchni Ziemi do nieskończoności nazywamy
drugą prędkością kosmiczną.
Aby tę prędkość znaleźć, należy skorzystać z zasady zachowania energii
mechanicznej. Pominiemy w tych obliczeniach opór powietrza, a więc warunki,
w jakich ta zasada jest spełniona, będą zachowane. Oznacza to, że energia statku na
powierzchni Ziemi Ep musi być równa energii E0 statku na orbicie. Warunek ten
prowadzi do zależności:
mv2p
GmM z mv 2orb GmM z



,
2
Rz
2
r
lub
mv2p
2

GmM z GmM z GmM z


.
Rz
2r
r
Dalsze przekształcenia prowadzą do wzoru:
14
io
 2 1
v p  GM z 
  .
R
 z r
Podstawiając r   otrzymujemy wyrażenie określające tę drugą prędkość kosmiczną:
v II 
2GM z
 vI 2 .
Rz
Podstawiając do tego wzoru dane, otrzymujemy następującą wartość drugiej
prędkości kosmicznej vII=11,2km/s.
Gdy na ciało będzie działać dodatkowo jakaś inna siła bezwładności, na przykład
siła związana z przyspieszeniem windy lub z ruchem po okręgu wokół Ziemi, ciężar
tego ciała będzie ulegał zmianom.
Gdy ciężar ciała jest większy niż to wynika z działania siły grawitacyjnej i siły
odśrodkowej bezwładności związanej z ruchem obrotowym (dobowym) Ziemi, wtedy
mówimy, że ciało to znajduje się w stanie przeciążenia. Gdy jednak siła grawitacyjna
i siły bezwładności działające na ciało równoważą się, wtedy mówimy, że ciało to
znajduje się w stanie nieważkości.
Kosmonauci, na przykład, znajdują się w stanie przeciążenia w chwili startu
rakiety nośnej, natomiast w stanie nieważkości są oni wówczas, gdy statek ten
znajduje się już na orbicie okołoziemskiej.
15