Temat: Drzewo algorytmu

Temat: Drzewo algorytmu.
1. Rodzaje drzew spotykane w informatyce:
a). drzewo folderów;
b). drzewo wyrażenia:
- argumenty wyrażenia (liczby lub zmienne) znajdują w wierzchołkach końcowych (wiszących) zwanych także
liśćmi, a działania są umieszczone w wierzchołkach pośrednich;
- np. drzewo wyrażenia: (6 + 3) * (5 – 3 * 4);
3
4
3
6
5
*
+
*
- np. drzewo wyrażenia: (x2 + y2)/(a – b);
/
+
-
( )2
( )2
x
y
a
b
c). drzewo algorytmu:
- drzewo rozwija się w dół;
- na górze jest korzeń, a połączenia (gałęzie), wskazując kierunek realizacji algorytmu skierowane są w dół;
- drzewo jest uproszczoną wersją schematu blokowego;
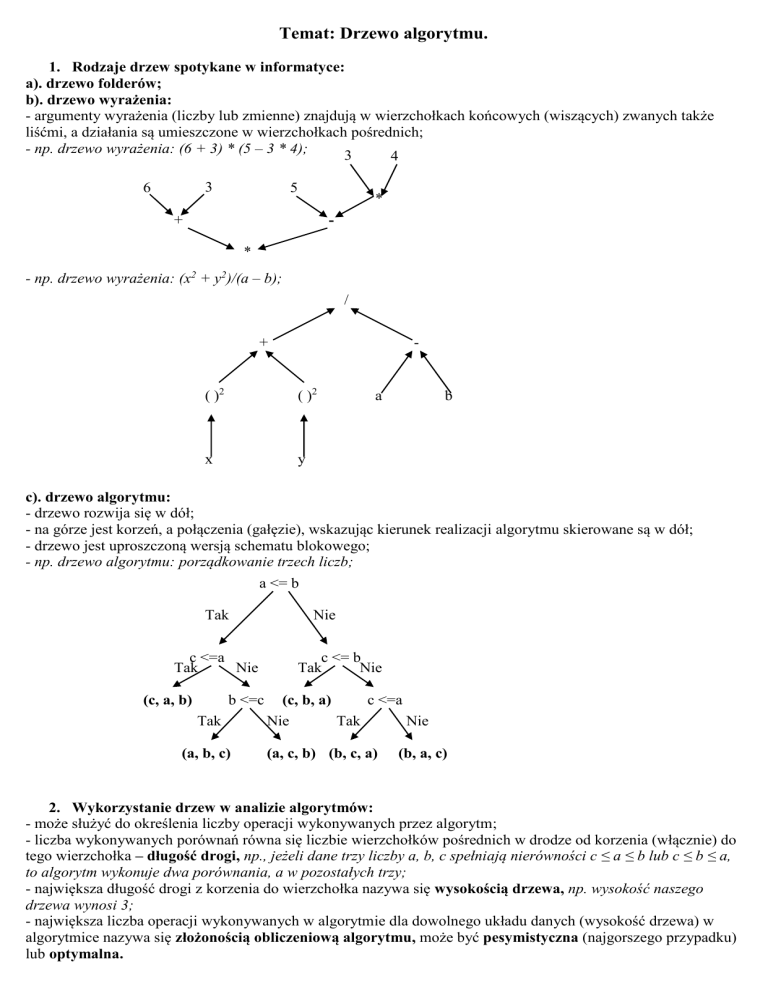
- np. drzewo algorytmu: porządkowanie trzech liczb;
a <= b
Tak
c <=a
Tak
Nie
b <=c
(c, a, b)
Tak
(a, b, c)
Nie
c <= b
Tak
Nie
c <=a
(c, b, a)
Nie
Tak
Nie
(a, c, b) (b, c, a)
(b, a, c)
2. Wykorzystanie drzew w analizie algorytmów:
- może służyć do określenia liczby operacji wykonywanych przez algorytm;
- liczba wykonywanych porównań równa się liczbie wierzchołków pośrednich w drodze od korzenia (włącznie) do
tego wierzchołka – długość drogi, np., jeżeli dane trzy liczby a, b, c spełniają nierówności c ≤ a ≤ b lub c ≤ b ≤ a,
to algorytm wykonuje dwa porównania, a w pozostałych trzy;
- największa długość drogi z korzenia do wierzchołka nazywa się wysokością drzewa, np. wysokość naszego
drzewa wynosi 3;
- największa liczba operacji wykonywanych w algorytmie dla dowolnego układu danych (wysokość drzewa) w
algorytmice nazywa się złożonością obliczeniową algorytmu, może być pesymistyczna (najgorszego przypadku)
lub optymalna.