1 - Gimnazjum nr 25

Załącznik do rozkładu materiału z fizyki
Powtórzenie z fizyki 2009 2010
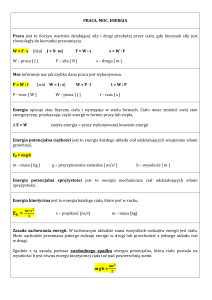
1.
Praca mechaniczna.
W  F r
W  F S
;
;
W
F  x;
1J
 1N 1m ;
m2
1J  1kg 2
s
;
J
1kWh  1000  1  3600s  3600000 J
s
Praca mechaniczna jest równa iloczynowi siły przez wektor przesunięcia, jeśli przesunięcie ciała jest równoległe do kierunku
F  r . Jeżeli kierunek przesunięcia jest prostopadły do działającej siły to siła ta nie wykonuje pracy.
 r W  0 . Jeśli sporządzimy wykres siły od przesunięcia to pole pod tym wykresem jest równe wykonanej pracy dla
działającej siły
Dla F
stałej siły (np. ciągnąc sanki wykonujemy pracę przeciwko sile tarcia i dla siły zmiennej np. podczas rozciągania sprężyny siła rośnie
wraz z wydłużeniem F  x .W jednym przypadku mamy pole prostokąta w drugim pole trójkąta. Jeżeli praca wykonywana jest
przeciwko sile tarcia to pracę liczymy ze wzoru W= F S
F
F
x
2.
x
Moc.
P
W
;
t
P
F S
 F v ;
t
1W 
1J
1s
;
1W  1kg
m2
s3
;
Mocą urządzenia (maszyny, człowieka) nazywamy iloraz pracy przez czas w którym ta praca została wykonana. Im szybciej (w
krótszym czasie) urządzenie wykona daną pracę tym jego moc jest większa.
3.
Energia.
Energią nazywany zdolność ciała do wykonania pracy (mówimy ciało ma energię, jeśli jest zdolne do wykonania pracy lub, że
energia to zmagazynowana praca). Aby ciało mogło wykonać pracę musimy wykonać pracę nad ciałem która w pewien sposób
zostanie w nim zmagazynowana w postaci energii potencjalnej grawitacji, energii potencjalnej sprężystości lub energii kinetycznej
ruchu.
4.
Energia potencjalna.
Energia potencjalna układu ciał (Ziemia-ciało) rośnie, jeśli wykonujemy nad tym układem ciał pracę siłami zewnętrznymi np.
podnosząc ciało z powierzchni ziemi działamy siłą zewnętrzną naszych mięśni przeciwko sile wewnętrznej wzajemnego
oddziaływania pomiędzy Ziemią a tym ciałem, (czyli przeciwko sile grawitacji). Aby podnieść ciało ruchem jednostajnym musimy
użyć siły równej, co do wartości sile grawitacji. Jednostką energii tak jak jednostką pracy jest dżul.
Energia potencjalna grawitacji.
E p  m  g  h ;
Ep  m  g  h ;
Ep  m ;
Ep  h ;
Jeżeli ciało spoczywa na powierzchni Ziemi h=0 nie posiada energii potencjalnej grawitacji.
5.
Energia kinetyczna.
Energia kinetyczna ciała jest związana z jego ruchem. Ciało będące w spoczynku (v=0)względem wybranego układu odniesienia nie
ma względem niego energii kinetycznej.
mv2
Ek 
2
lub
Ek 
1 2
mv ;
2
Ek  m ;
Ek  v 2 ;
Energia kinetyczna zależy proporcjonalnie od kwadratu prędkości ciała, jeśli prędkość wzrośnie 4 razy Ek wzrośnie 16 razy, jeśli
prędkość ciała zmaleje 3 krotnie Ek zmaleje 9-cio krotnie.
6.
Zasada zachowania energii mechanicznej.
Energią mechaniczną ciała nazywamy sumę jego energii potencjalnej i kinetycznej.
Zasada energii mechanicznej mówi że w polu sił zachowawczych (pole grawitacyjne i elektryczne), całkowita energia mechaniczna
układu ciał jest stała. Należy przez to rozumieć że suma energii potencjalnej i kinetycznej ciała jest stała. Jeśli zmniejsza się jedna z
tych energii o pewną wartość to druga rośnie o tę samą wartość. Jeśli jedna z energii się zmniejsza a druga z nich nie rośnie
oznacza to że musi być wykonywana praca kosztem zmniejszającej się energii. Zasada zachowania energii nie jest zachowana w
przypadku przemieszczania się ciał w obecności sił tarcia, ponieważ podczas przesunięcia jest wykonywana praca przeciwko sile
tarcia.
Ek=0 v=0
h=max Ep=max
Na rysunku obok przedstawione jest zagadnienie rzutu
E p  Ek  const .
pionowego w którym Ek podczas wyrzutu zamienia się
całkowicie w energię potencjalną grawitacji. Jeśli pominiemy opory powietrza. Maksymalna energia kinetyczna przy
wyrzucie jest równa maksymalnej energii potencjalnej na
maksymalnej wysokości, na którą wzniesie się ciało
możemy zapisać. Ekmax=Epmax stąd mv2/2=mgh po
v
skróceniu mas otrzymamy następujące równanie
v2/2=gh. Równanie to możemy wykorzystać również dla
Ek=max v=max
h=0 Ep=0
spadku swobodnego ciał. Wysokość, na którą wzniesie się
ciało nie zależy od jego masy a tylko prędkości wyrzutu.
3
Załącznik do rozkładu materiału z fizyki
Powtórzenie z fizyki 2009 2010
7.
r2
Maszyny proste.
F1
r2
r1
l
h
r1
F2
F1
Dźwignia dwustronna
Warunek równowagi dzwigni
F2
Dźwignia jednostronna
Równia pochyła
F1  r1  F2  r2 , gdzie: F1 i F2 - siły działające (może być też ciężar Q) r1 i r2 - długość ramion
odległość od siły do punktu podparcia dzwigni.
Praca wykonana na równi pochyłej podczas podnoszenia ciała na wysokość h jest równa pracy przy wtaczaniu tego ciała (bez tarcia)
po równi gdzie: l - długość równi. W1=W2 czyli
8.
F1  h  F2  l
Właściwości i budowa materii.
Ciała stałe ciecze i gazy mają budowę ziarnistą tzn. są zbudowane z atomów lub cząsteczek wielkość atomów i cząsteczek jest różna
dla różnych substancji. Potwierdzają to takie zjawiska jak dyfuzja czy mieszanie się cieczy.
Dyfuzja jest to samoistne rozprzestrzenianie się cząsteczek jednej substancji w drugiej. Szybkość dyfuzji zależy od temperatury.
Najszybciej dyfuzja zachodzi w gazach najwolniej w ciałach stałych. Przyczyną dyfuzji są tzw. ruchy Brown’a.
Ciała stałe – mają własny kształt i objętość trudno zmienić kształt i objętość ciał stałych. Cząsteczki są ułożone blisko siebie, silnie ze
sobą oddziałują, ułożone są w sposób regularny tworząc tzw. sieć krystaliczną. Cząsteczki ciał stałych poruszają się ruchem
drgającym wokół położenia równowagi. Ciała stałe posiadają cechy mechaniczne takie jak: plastyczność, sprężystość, kruchość.
Ciecze – nie mają własnego kształtu (kształt naczynia), mają własną objętość, którą trudno zmienić (są nieściśliwe). Cząsteczki są
blisko siebie, znajdują się w ciągłym chaotycznym ruchu, słabo ze sobą oddziałują.
Gazy – nie mają własnego kształtu i objętości łatwo zmienić ich objętość, ponieważ cząsteczki są daleko od siebie, poruszają się
ruchem chaotycznym, oddziałują na siebie tylko podczas zderzeń.
Oddziaływania międzycząsteczkowe możemy podzielić na siły spójności Fs i siły przylegania Fp. Siły spójności występują pomiędzy
cząsteczkami tej samej substancji siły przylegania występują pomiędzy cząsteczkami stykających się ciał. Siły spójności są przyczyną
powstawania menisków cieczy w naczyniu jeśli Fs> Fp to menisk jest wypukły jeśli Fs< Fp to menisk jest wklęsły.
rtęć - szkło
woda - szkło
Rozszerzalność temperaturowa ciał stałych cieczy i gazów - polega na zwiększaniu ich wymiarów i objętości wraz ze wzrostem
temperatury. Wzrost wymiarów ciał jest tym większy im większy jest ich rozmiar początkowy i przyrost temperatury. Bardzo ważną
cechą rozszerzalności jest anomalne zjawisko rozszerzalności wody. Woda najmniejszą objętość ma w temperaturze 4 oC czyli ma w
tej temperaturze największą gęstość dlatego zawsze na dnie zbiorników wodnych i rzek woda o tej temperaturze znajduje się przy
samym dnie. Rozszerzalność temperaturową cieczy wykorzystuje się do budowy termometrów (rtęć alkohol).
Gęstość substancji – gęstością substancji nazywamy iloraz masy substancji przez objętość którą zajmuje. Informuję nas o ilości
substancji podanej w kg jaka znajduje się w jednostce pojemności.

m
V
;
m V ;
jednostkami gęstości są
g
kg
;
3
cm dm3
;
kg
m3
1m3=1000dm3=1000 000cm3
1m=10dm=100cm stąd 1m3=1m1m1m=10dm10dm10dm=100cm100cm100cm
1
kg
g
1
1000000 1
kg
1000
5 3 5
 5
kg 
 5000 3
3
1
1
1
cm
1000
1
m
m
m
m
m
100 100 100
kg
1000 g
g
2700 3  2700
 2,7 3
m
100cm  100cm  100cm
cm
9.
Zmiany stanów skupienia substancji (przemiany fazowe).
Ciała mogą znajdować się w trzech stanach skupienia – stan stały, stan ciekły, stan lotny (gazowy)
Ciało stałe (topnienie)  Ciecz (parowanie)  Para (skraplanie)  Ciecz (krzepnięcie)  Ciało stałe możliwa są też inne przemiany
Ciało stałe (sublimacja)  Para (resublimacja)  Ciało stałe
Przykładem sublimacji jest wysychanie mokrego prania na mrozie, przykładem resublimacji jest osadzanie się szronu.
10. Energia wewnętrzna ciał, sposoby przekazywania energii cieplnej, I zasada termodynamiki.
Energia wewnętrzna ciał EW jest równa sumie energii kinetycznej chaotycznego (cieplnego) ruchu cząsteczek i energii potencjalnej
wynikającej z wzajemnego oddziaływania pomiędzy cząsteczkami.
Energię cieplną możemy przekazywać ciałom na trzy sposoby. Przez tzw. cieplny przepływ energii, konwekcję i promieniowanie.
Cieplny przepływ energii polega na przekazywaniu energii kinetycznej chaotycznego (cieplnego) ruchu cząsteczek od cząsteczek o
wyższej energii (temperaturze) cząsteczką sąsiednim o niższej energii (temperaturze) odbywa się to najczęściej w ciałach stałych.
Konwekcja jest to unoszenie się cieplejszych części gazów i cieczy do góry (mniejsza gęstość) i opadaniu zimniejszych części cieczy i
gazów ten sposób wymiany ciepła wykorzystywany jest przy ogrzewaniu budynków za pomocą kaloryferów. Energię cieplną możemy
też przekazywać poprzez promieniowanie. Główny źródłem energii cieplnej na Ziemi jest energia przekazana od Słońca przez
promieniowanie.
Materiały, które dobrze przewodzą ciepło nazywamy przewodnikami ciepła (głównie metale). Materiały, które źle przewodzą ciepło
to tzw. izolatory cieplne (porcelana, szkoło, styropian, drewno, tworzywa sztuczne). W termosach, które służą do utrzymywania
stałej temperatury wewnątrz stosuje się naczynie o podwójnych ściankach, pomiędzy którymi znajduje się próżnia, co uniemożliwia
wymianę ciepła z otoczeniem.
4
Załącznik do rozkładu materiału z fizyki
Powtórzenie z fizyki 2009 2010
EW  Q  W ; gdzie: EW
wzrost energii wewnętrznej ciała,
Q -dostarczone ciepło W - praca wykonana nad ciałem
Aby spowodować wzrost temperatury ciała musimy mu dostarczyć energii (ciepła Q). Ilość dostarczonego do ciała ciepła jest wprost
proporcjonalna do jego masy m i przyrostu temperatury T=(TK-T0), jaki chcemy spowodować:
Q  m  T ; Ilość dostarczonego ciepła jest proporcjonalna do iloczynu masy ciała i
Q  T ;
Qm;
przyrostu jego temperatury. Jeśli wielkości są do siebie proporcjonalne to ich iloraz ma wartość stałą, i w tym wypadku nazywa się
ciepłem właściwym substancji cW.
cW 
Q
J
 const ; dla wody ciepło właściwe wynosi 4200 
m  T
kg C
oznacza to, że
aby zwiększyć temperaturę wody o masie 1 kg o 1 oC należy dostarczyć jej energii (ciepła) o wartości 4200 J. Każda substancja ma
inne ciepło właściwe. Przekształcając powyższe równanie możemy obliczyć ile ciepła należy dostarczyć do ciała o określonej masie
 cW  m  T . Jeśli jedno z ciał oddaje ciepło innemu ciału o niższej temperaturze
(np. poprzez zmieszanie cieczy o różnych temperaturach) to spełnione jest równanie QO  QP gdzie: QO – ciepło oddane; QP –
m, aby podnieść jego temperaturę o T. Q
ciepło pobrane, jest to tzw. bilans cieplny.
11. Topnienie, krzepnięcie, parowanie i skraplanie.
Topnienie i krzepnięcie ciał odbywa się w stałej temperaturze (tzw. temperaturze topnienia danej substancji). Temperatury topnienia
i krzepnięcia danej substancji są sobie równe, ciało topi się, gdy dostarczamy mu energii w postaci ciepła, krzepnie wtedy, gdy ciało
oddaje ciepło np. do otoczenia.
Ciało paruje w temperaturze wrzenia, to określenie odnosi się do gwałtownego parowania cieczy w stałej temperaturze z całej jej
objętości. Para skrapla się też w temperaturze wrzenia podczas oddawania ciepła (np. podczas zetknięcia się z ciałem o niższej
temperaturze, co obserwujemy no pokrywce naczyń, w których gotowana jest woda). Stałość temperatury topnienia, krzepnięcia,
parowania i skraplania pomimo dostarczaniu lub odbieraniu ciepła tłumaczymy tym, że podczas przemian fazowych, ciepło jest
oddawane lub pobierane na proces zmiany stanu skupienia.
T
T
Q1
TS
TW
Q2
Q4
Tt
Q3
Tk
Q3
Q4
t
Q2
t
Q1
TW – temperatura wrzenia
Tt – temperatura topnienie
Q1 – ciepło dostarczone do ogrzania ciała stałego do Tt
Q2 – ciepło potrzebne do stopienia ciała w Tt
Q3 – ciepło dostarczone do ogrzania cieczy do TW
Q4 – ciepło potrzebne do wyparowania cieczy w TW
TS – temperatura skraplania
Tk – temperatura krzepnięcia
Q1 – ciepło oddane podczas skraplania w TS
Q2 – ciepło oddane przez ciecz podczas ochładzania do Tk
Q3 – ciepło oddane przez ciecz podczas krzepnięcia w Tk
Q4 – ciepło oddane przez ciało stałe podczas oziębiania
Ciepło Q1 i Q3 obliczamy z poznanego wcześniej wzoru
Ciepło Q2 i Q4 obliczamy z poznanego wcześniej wzoru
Natomiast ciepło potrzebne do stopienia w tempera-turze
topnienia i wyparowania ciał w temperaturze wrzenia ciała
obliczamy z równań:
Natomiast ciepło oddane podczas skraplania i krzepnięcia
ciał w temperaturze skraplania i krzepnięcia obliczamy z
równań:
Q  c  m  T
Q2  ct  m ;
gdzie:
Q  c  m  T
Q1  cS  m ;
Q4  c p  m ;
gdzie:
ct – ciepło topnienia;
cp- ciepło parowania w temperaturze wrzenia
Q2 i Q4  m
Q
ct  ;
m
cp 
Q1 i Q3  m
Q
cS  ;
m
Q
;
m
Q3  ck  m ;
cS – ciepło skraplania;
ck- ciepło krzepnięcia;
ck 
Q
;
m
Z powyższych wykresów przemian fazowych widać, że Tt=Tk oraz TW=TS dla danej substancji. Także ilość ciepła pobieranego jak i
oddawanego podczas topnienia i krzepnięcia oraz wrzenia i skraplania przez daną masę tej samej substancji są jednakowe stąd ct=ck
oraz cW=cS.
Przykładowe zadania Ile energii (ciepła) należy dostarczyć oby zagotować szklankę wody o masie m=0,250 kg, która znajduje się w
temperaturze pokojowej T0=20 oC . Ciepło właściwe wody c=4200 J/kgoC.
Q  c  m  T ; T  Tk  T0  100 C  20 C  80 C ; Q  4200
J
 0,25kg  80C ; Q  84kJ

kg C
Oblicz, jaką masę lodu można stopić spalając węgiel, jeżeli podczas spalania wydzieli się 400kJ. Ciepło topnienia lodu w
temperaturze topnienia wynosi 120 kJ/kg.
Q  ct  m ;
m
Q 400000 J

 3,5kg ;
ct 120000 J
kg
5