wykład 1 - CHEMIA FIZYCZNA - dr inż. Bernadeta Andruszkiewicz

WYKŁAD 2_1
1. Pojęcie fazy i składnika
Faza to taka część układu, która jest jednorodna pod względem fizycznym i chemicznym
oraz oddzielona jest od obszarów układu o innych właściwościach powierzchnią. Na powierzchni tej następuje
skokowa zmiana właściwości.
Przykład 1 - mieszanina ciekłej wody i kostek lodu.
Suma wszystkich kawałków lodu to jedna faza, woda ciekła to druga faza.
(DWIE FAZY – STAŁA I CIEKŁA, JEDEN SKŁADNIK – H2O)
Przykład 2 - mieszanina benzenu i toluenu w temperaturze 50C p=1atm.
Roztwór ciekły (benzen+toluen), a nad nim opary – też dwuskładnikowe.
Jest to układ dwufazowy (ciecz-para) dwuskładnikowy (benzen+toluen).
Dla układu jednoskładnikowego (substancja czysta) jakie są możliwe fazy? - gazowa (tylko jedna), ciekła (też
tylko jedna), stałe ( niektóre substancje występują w różnych odmianach polimorficznych).
Definicja fazy odnosi się do skali makro. Różnice mikro (np. fluktuacje gęstości ) nie są uwzględniane.
2. Nazewnictwo w przemianach fazowych
Przemiana cieczgaz to parowanie (wrzenie); przemiana gazciecz to skraplanie (kondensacja).
Przemiana cieczciało stałe to krystalizacja (krzepnięcie); przemiana ciało stałeciecz to topnienie.
Przemiana ciało stałegaz to sublimacja; przemiana gazciało stałe to resublimacja.
3. Reguła faz Gibbsa – diagramy fazowe
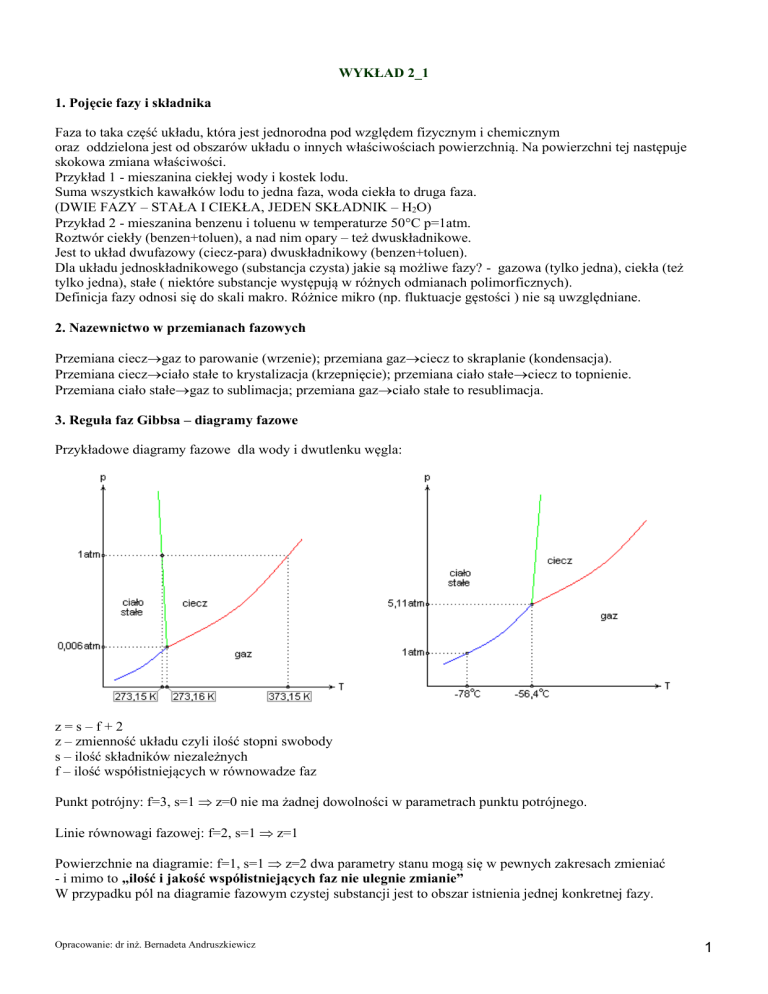
Przykładowe diagramy fazowe dla wody i dwutlenku węgla:
z=s–f+2
z – zmienność układu czyli ilość stopni swobody
s – ilość składników niezależnych
f – ilość współistniejących w równowadze faz
Punkt potrójny: f=3, s=1  z=0 nie ma żadnej dowolności w parametrach punktu potrójnego.
Linie równowagi fazowej: f=2, s=1  z=1
Powierzchnie na diagramie: f=1, s=1  z=2 dwa parametry stanu mogą się w pewnych zakresach zmieniać
- i mimo to „ilość i jakość współistniejących faz nie ulegnie zmianie”
W przypadku pól na diagramie fazowym czystej substancji jest to obszar istnienia jednej konkretnej fazy.
Opracowanie: dr inż. Bernadeta Andruszkiewicz
1
4. Izotermiczno – izobaryczny charakter przemian fazowych
Przykład – 18g lodu (wody w stanie stałym ) o temperaturze -10C ( p=1atm) ogrzewano doprowadzając ciepło w
tempie 100J na minutę. Narysować wykres zmian temperatury w funkcji czasu.
DANE
CP (st)  40
J
molK
H top  6000
J
mol
C P (c)  75
J
molK
H par  40700
C P (g )  36
J
molK
molowe pojemności cieplne wody w różnych stanach
skupienia
entalpia topnienia i entalpia parowania wody
J
mol
Rysunek nosi nazwę krzywej ogrzewania lub - w przypadku odprowadzania ciepła - krzywej chłodzenia.
Odcinki poziome na krzywej ogrzewania to przemiany fazowe.
Dopóki są obecne dwie fazy (np. po 139 minutach ogrzewania obecne są ciecz i para), dopóty przy p=1atm
temperatura nie może być inna niż 100C. Dostarczane ciepło całe idzie na przemianę cieczy w parę.
18g H2O(para)
373K,1atm

18g H2O(ciecz)
Vp 
m3
mol
 40,73kJ / mol
VC  0,000018
H par
U par  H par  (p  Vp  p  VC )  40,73kJ / mol  101325
Opracowanie: dr inż. Bernadeta Andruszkiewicz
RT 8,314  373 m 3

p
101325 mol
Vp  0,0306
N
m2
 (0,0306  0,000018)
m3
mol
m3
 (40,73  3,10)kJ / mol
mol
2
Objętość mola cieczy jest pomijalnie mała w porównaniu z objętością powstającej z niej pary.
Objętość mola ciała stałego jest pomijalnie mała w porównaniu z objętością powstającej z niego pary.
Objętość jednego mola cieczy i objętość 1 mola ciała stałego są podobnego rzędu – żadnych uproszczeń przy
odejmowaniu takich porównywalnych wielkości.
5. Entalpia przemian fazowych zależy od temperatury (na przykładzie parowania).
Droga okrężna i droga wprost procesu parowania w temperaturze T2 mają tę samą entalpię.
T1
T2
H(T2 )   C P (ciecz )dT  H(T1 )   C P (gaz )dT
T2
T1
T2
H(T2 )  HT1    (C P (gaz )  C P (ciecz ))dT
T1
T2
H(T2 )  HT1    C P dT
 prawo Kirchhoffa dla swoistej reakcji H2O(ciecz )  H2O(gaz )
T1
Ponieważ CP (ciecz )CP (gaz ) , to H parowania spada w miarę wzrostu temperatury.
Linia parowania „gruba” przy punkcie potrójnym, „cienka” ( do zera ) przy punkcie krytycznym.
6. Entalpia reakcji w przedziale temperatur obejmującym przemiany fazowe
Zadanie a). Obliczyć standardową entalpię reakcji uwodornienia benzenu (ciecz)
do cykloheksanu(ciecz) w temperaturze 298K. Dane są standardowe entalpie tworzenia reagentów.
C6H6(c) + 3H2(g)  C6H12(c)
T=298K, p=1atm
(1)
(2)
(3)
H tw1  49,1kJ / mol ; H tw3  156,2kJ / mol
H   H twi   i    (H twj   j )  H tw3  3H tw2  H tw1  (156,2  49,1)kJ / mol  107,1kJ / mol
prod
substr
Opracowanie: dr inż. Bernadeta Andruszkiewicz
3
Zadanie b). Obliczyć entalpię reakcji uwodornienia benzenu do cykloheksanu w temperaturze 350K.
W jakich stanach skupienia będą poszczególne reagenty? Dana temperatura wrzenia benzenu
Twrz1=353,3K,temperatura wrzenia cykloheksanu Twrz3=353,8K , molowe pojemności cieplne reagentów wynoszą:
CP1  136,1J / molK; C P2  28,8J / molK; CP3  156,5J / molK;
C6H6(c) + 3H2(g)  C6H12(c)
(1)
(2)
(3)
T=350K, p=1atm
350K
H(350)  H(298)   (C P3  3  C P 2  C P1 )dT  107100
298K
J
J
 (156,5  3  28,8  136,1)
 350  298K
mol
molK
H(350)  (107,1  3,43)kJ / mol  103,67kJ / mol
Zadanie c). Obliczyć entalpię reakcji uwodornienia benzenu do cykloheksanu w temperaturze 353,5K.
W jakich stanach skupienia będą poszczególne reagenty? Dana jest temperatura wrzenia benzenu Twrz1=353,3K,
temperatura wrzenia cykloheksanu Twrz3=353,8K. Molowe pojemności cieplne reagentów wynoszą:
C p1 (ciecz )  136,1J / molK; C p1 (gaz)  81,7J / molK ; C p 2  28,8J / molK ; C p3 (ciecz)  156,5J / molK ;
entalpia parowania benzenu Hpar1=30,8kJ/mol
C6H6(g) + 3H2(g)  C6H12(c)
(1)
(2)
H(353,5) 
T=353,5K, p=1atm
(3)
353, 3 K

C p1 (gaz)dT  H par1 
353, 5 K
298K

353, 3 K
C p1 (ciecz)dT 3 
298K

C p 2 dT  H (298 ) 
353, 5 K
353, 5 K
 C p 3 (ciecz)dT
298K
H(353,5)  (353,3  353,5)K  81,7 J / molK  30800 J / mol  (298  353,3)K  136 ,1J / molK 
 3  ( 298  353,5) K  28,8J / molK  107100 J / mol  (353,5  298 )K  156 ,5J / molK
H(353,5)  (107 ,1  30,8  0,02  7,53  4,80  8,69) kJ / mol  72,64 kJ / mol
Zadanie d). Obliczyć entalpię reakcji uwodornienia benzenu do cykloheksanu w temperaturze 473K.
W jakich stanach skupienia będą poszczególne reagenty? Dana temperatura wrzenia benzenu Twrz1=353,3K,
temperatura wrzenia cykloheksanu Twrz3=353,8K
Jest to zadanie nr 10 ze zbioru zjazd 2_1. Powodzenia w jego rozwiązywaniu!
Opracowanie: dr inż. Bernadeta Andruszkiewicz
4
7. Zadanie domowe nr 1
W reaktorze przy stałym ciśnieniu 1atm ulega całkowitemu spaleniu mieszanina 2,2 mola metanu(A) i 3,3 mola
etanu(B).w nadmiarze powietrza ( =real/minim=1,3 ) . Temperatura początkowa 298K.
Skład powietrza 80%N2 20%O2 .
1.Jaka część ciepła reakcji zużyje się na podgrzanie mieszaniny poreakcyjnej do 100C
i odparowanie obecnej tam wody?
2. Jaka jest temperatura w reaktorze, jeśli 30% ciepła reakcji stanowią straty do otoczenia?
3. Jaką podaż powietrza zastosować, aby nie dopuścić do przegrzania reaktora (TK 750C )
Przyjąć, że straty ciepła do otoczenia wynoszą 30% ciepła reakcji.
Zastosować następujące oznaczenia:
2,2mola A
3,3 mola B
?O2(g)
?N2(g)
Qr
298K
?O2(g)
?N2(g)
?CO2(g)
?H2O(c)
298K
q1
?O2(g)
?N2(g)
?CO2(g)
?H2O(c)
q2
373K
?O2(g)
?N2(g)
?CO2(g)
?H2O(g)
qstr
q3
373K
?O2(g)
?N2(g)
?CO2(g)
?H2O(g)
TK
ROZWIĄZANIE
1. Dane znalezione w Poradniku Fizykochemicznym (WNT, 1974)
l.p.
substancja standardowa entalpia
molowa pojemność cieplna w funkcji temperatury,
entalpia
parowania
J/mol.K
tworzenia
C pi  a i  b i  T  d i  T 2
ai
1
2
3
4
5
6
7
metan
etan
woda ciekła
woda gazowa
tlen
azot
dwutlenek
węgla
-74,85kJ/mol
-84,67kJ/mol
-285,9kJ/mol
-393,52kJ/mol
+40,66kJ/mol
30,12J/molK
36,17J/molK
27,83J/molK
44,15J/molK
bi
di
średnio 75,15J/mol.K
11,30 103 J / molK 2
0,84 103 J / molK 2
-4,31 105 JK / mol
4,18 103 J / molK 2
9,04 103 J / molK 2
-8,54 105 JK / mol
2. Bilans materiałowy
CH4(g)  2O2(g)  CO2(g)  2H2O(c)
Minimalna ilość moli tlenu potrzebna do reakcji to 2,2  2  4,4molaO 2
Realna ilość tlenu to 4,4 1,3  5,72molaO2 . Tej ilości tlenu towarzyszy 5,72  4  22,88molaN 2
Z powodu zajścia reakcji spalania metanu wytworzy się 2,2 1  2,2molaCO2 oraz 2,2  2  4,4molaH 2O
C 2 H 6( g ) 
7
O 2(g )  2CO 2(g )  3H 2O(c)
2
Minimalna ilość moli tlenu potrzebna do reakcji to 3,3  3,5  11,55molaO2
Realna ilość tlenu to 11,55 1,3  15,015molaO2 . Tej ilości tlenu towarzyszy 15,015  4  60,06molaN2
Z powodu zajścia reakcji spalania etanu wytworzy się 3,3  2  6,6molaCO2 oraz 3,3  3  9,9molaH 2O
Opracowanie: dr inż. Bernadeta Andruszkiewicz
5
Podsumowanie bilansu materiałowego:
l.p.
1
2
3
4
5
6
7
substancja
przed
reakcją
metan
2,2 mola
etan
3,3 mola
woda ciekła
0
woda gazowa 0
tlen
20,735 mola
azot
82,94 mola
dwutlenek
0
węgla
po reakcji
0
0
14,3 mola
0
4,785 mola
82,94 mola
8,8 mola
3. Obliczam molową entalpię spalania metanu i molową entalpię spalania etanu w temperaturze 298K.


Htwj j    393,51 2   285,9 3kJ / mol   84,67 1kJ / mol  1560,05kJ / mol
H1   H twii    H twj j   393,51 1   285,9  2kJ / mol   74,85 1kJ / mol  890,46kJ / mol
prod
substr
prod
substr
H2   H twii   
4. Obliczam ciepło reakcji chemicznych.
Qr  n1  H1  n2  H2  2,2mola  890,46kJ / mol  3,3mola  1560,05kJ / mol  7107,177kJJ
5. Obliczam ciepło potrzebne na ogrzanie mieszaniny poreakcyjnej od temperatury 298K do temperatury 373K w
warunkach izobarycznych.
373
373
373
373
298
298
298
373
298
q1  n 3   Cp3dT  n 5   Cp5dT  n 6   Cp6dT  n 7   Cp7dT  14,3mola  75,15
373

n 5   a 5  b5  T  d 5  T
2
dT  n
5
298


373

J
 373  298K 
molK

2
2
 a 6  b6  T  d 6  T dT  n 7   a 7  b7  T  d 7  T dT 
298
298
373
373
373
298
298
298
2
 n 5  a 5  n 6  a 6  n 7  a 7 dT   n 5b5  n 6  b6  n 7  b7   TdT   n 5  d5  n 6  d 6  n 7  d 7   T dT
q1  300,194kJ
6. Obliczam ciepło potrzebne do odparowania wody w temperaturze 373K w warunkach izobarycznych.
q 2  40,66
kJ
 14,3mola  581,438kJ
mol
7. Obliczam straty ciepła do otoczenia (przy założeniu 30%)
q str  0,3  Q r  0,3  7107,177kJ  2132,153kJ
8. Obliczam ilość ciepła, jaka pozostaje na ogrzanie mieszaniny poreakcyjnej powyżej 373K.
Q r  0,7  q1  q 2  q 3  0
q 3  4093,392kJ
9. Oszacowuję temperaturę końcową, zakładając, że średnia wartość molowej pojemności cieplnej każdego
składnika mieszaniny poreakcyjnej wynosi 35J/molK.
(Tprzybl  373K ) 
q3
4093392J

 1055K  Tprzybl  1428K
(n 4  n 5  n 6  n 7 )  Cpśś 110,825moli  35J / molK
Ta orientacyjna wartość jest mi potrzebna, aby móc od czegoś zacząć założenia w kolejnych przybliżeniach
obliczeń z całkami.
Niewiadoma temperatura końcowa występuje w wielomianie trzeciego stopnia i analityczne rozwiązywanie byłoby
kłopotliwe:
Tk
Tk
373
373
Tk
Tk
373
373
q 3  n 4   C p 4dT  n 5   C p5dT  n 6   C p 6dT  n 7   C p 7 dT 
Tk
Tk
Tk
373
373
373
  ( n 4a 4  n 5a 5  n 6a 6  n 7a 7 )dT   (n 4 b 4  n 5b5  n 6 b6  n 7 b 7 )  TdT   ( n 4d 4  n 5d 5  n 6d 6  n 7d 7 )  T  2dT
q3  (n 4a 4  n 5a 5  n 6a 6  n 7a 7 )  Tk  373K  
 ( n 4 b 4  n 5b5  n 6 b 6  n 7 b 7 ) 


 1
1
1 
 Tk2  3732 K 2  (n 4d 4  n 5d5  n 6d 6  n 7d 7 )   1  


2
373K 
 Tk

Opracowanie: dr inż. Bernadeta Andruszkiewicz
6
10. Metodą kolejnych przybliżeń szukam takiej wartości Tk,, aby obliczona wartość q3 była możliwie bliska
wartości 4093392J.
Tkzałożone
q3obliczone
1428K
1450K 1446K
1445K
4025kJ 4116,6kJ 4099,9kJ 4095,8kJ
1444K
4091,66kJ
Wynik
1444,5K
11. Obliczam ilość ciepła q 3' jaka wystarcza do podgrzania mieszaniny poreakcyjnej do temperatury
(750+273)K=1023K. Jeśli okaże się, że jest to mniej niż q3 oznaczać to będzie, że przy α=1,3 reaktor ogrzałby się
za mocno i że trzeba będzie wziąć więcej powietrza, aby do tego przegrzania nie dopuścić.
q 3'  (n 4 a 4  n 5 a 5  n 6 a 6  n 7 a 7 )  1023K  373K  


1
1 
 1
 (n 4 b 4  n 5 b 5  n 6 b 6  n 7 b 7 )   1023 2 K 2  373 2 K 2  (n 4 d 4  n 5 d 5  n 6 d 6  n 7 d 7 )   1  


2
 1023K 373K 
q 3'  (3300 ,5  650  591,85  907,4  95,775  170,34)kJ  2666 ,06kJ
q  q 3  q ,3  (4093,39  2666 ,06)kJ  2661,96kJ nadwyżka ciepła, którą trzeba zagospodarować, aby się
reaktor nie przegrzał. Jeśli wezmę więcej powietrza od początku, to ono nie będzie brało udziału w reakcji, tylko
będzie balastem pochłaniającym energię na swoje podgrzanie od 298K do 1023K.
Na 1 mol powietrza na podgrzanie w tych granicach temperatur potrzeba:

1023 2  298 2
 1000 1000 
q m  0,8  27,83  0,2  36,17   725  0,8  4,18  0,2  0,84  
 0,8  431  

 J
2000
 1023 298 

q m  21386 ,05J  1681,77 J  785,75J  22,282 kJ na każdy mol powietrza.
Aby temperatura reaktora nie przekroczyła 1023K, należy dodatkowo włączyć do układu
q
2661,96kJ
n dod 

 119,5 mola dodatkowego powietrza, co oznacza pracę reaktora z parametrem
q m 22,282 kJ / mol
20,735  0,2  119,5

 2,8 zamiast 1,3.
20,735  4,785
Opracowanie: dr inż. Bernadeta Andruszkiewicz
7