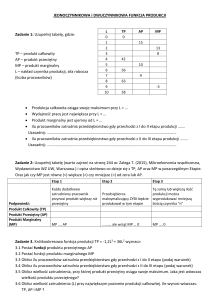
Wprowadzenie
Po co uczyć (się) teorii ekonomii?
• a po co uczyć matematyki? - ćwiczenie umysłu
• żeby oswoić studentów z terminologią – później pisząc pracę
magisterską czy też komunikując się z innymi nie muszą wymyślać
własnej
• bo uczy logicznego podejścia do praktycznych problemów
• uwaga: uczymy tzw. neoklasycznej teorii ekonomii, nie jest to jedyne
ujęcie, ale jedyne koherentne i w zasadzie kompletne
Mikroekonomia II
�
Mikroekonomia II (B)
�
�
�
�
�
�
�
12
Funkcje produkcji
Funkcje kosztów
Optymalny wybór producenta
Doskonała konkurencja
Monopol
Teoria gier
Modele oligopolu
Decyzje produkcyjne firmy
�
Analogia z wyborem konsumenta:
�
�
�
�
Wybory produkcyjne firmy:
�
�
�
�
�
Preferencje
Ograniczenie budżetowe
Optymalny wybór maksymalizujący użyteczność
Technologia produkcji (czynniki, produkty)
Koszty (ceny czynników produkcji)
Optymalny wybór czynników
Jak zmieniają się łączne koszty ze zmianą wielkości
produkcji
Jak zmieniają się zyski ze zmianą wielkości produkcji
13
Funkcje produkcji
�
�
�
�
Czynniki produkcji (inputs) -> produkty (outputs)
Technologia to proces przemiany czynników w produkty
Często do dyspozycji jest kilka alternatywnych technologii
Czynniki produkcji:
�
�
�
�
�
Kaapitał
pitał (ca
apital
pital, K
K))
Praca (labor, L)
Materiały
Ziemia
Funkcja produkcji – obrazuje najwyższą możliwą
produkcję z danej kombinacji czynników dla danej
technologii
q = f ( K, L)
14
Funkcje produkcji
�
�
�
Ujęcie statyczne
Jaka możliwość zmiany ilości czynników?
Krótki okres (short run, SR)
�
�
�
Przynajmniej jeden z czynników stały
Najdłuższy czas w którym przynajmniej jeden z czynników
produkcji stosowanych w procesie produkcji nie może się
zmienić
Długi okres (long run, LR)
�
�
15
Wszystkie czynniki zmienne
Najkrótszy czas konieczny do zmiany ilości wszystkich
czynników produkcji stosowanych w procesie produkcji
Krótki okres – jeden czynnik zmienny
q = f ( L)
16
Analiza wielkości produkcji
�
Średnia produktywność czynnika (average product)
�
Wielkość produkcji na jednostkę czynnika
q
P rodukcja
APL =
=
I lo ś ć Czynnika L
17
Analiza wielkości produkcji
�
Krańcowa produktywność czynnika (marginal product)
�
Dodatkowa produkcja spowodowana zwiększeniem
zatrudnienia czynnika o jedną jednostkę
Δq
Δ Produkcji
=
M PL =
o ś ccii Czynnika
Ilo
C zynn ik a ΔL
Δ Il
�
Krańcowa = w granicy = pochodna cząstkowa:
Δq ∂ f ( L )
M PL = lim
=
ΔL → 0 ΔL
∂L
18
Analiza wielkości produkcji
19
Funkcja produkcji – wykres
q
Całkowita produkcja
D
112
D – produkcja maksymalna
P–n
achylenie
ółłp
rostej
A
lenie p
AP
nachy
pó
proste
ze środka układu wsp.
MP – nachylenie stycznej w
danym punkcie
C – AP maksymalne
B – AP = 20
A – MP = 20
C
60
B
A
0 1
20
2
3
4
5 6
7
8
9
10
L
Krańcowa i średnia produktywność – wykres
• MP przecina AP w E,
• W E: MP = AP => maksimum AP
• Na lewo od E: MP > AP => AP rośnie
• Na prawo od E: MP < AP => AP maleje
q
• Dla L = 8, MP = 0 i q = max
30
rańcowa
roduktywność
K
ńcowa p
ść
Kra
produktywno
E
20
Średnia produktywność
10
L
0 1
2
3
4
5 6
7
8
9
10
21
Wykresy funkcji produkcji i produktywności – wnioski
�
�
�
�
�
Gdy krańcowa produktywność większa od średniej
produktywności – średnia produktywność rośnie
Gdy krańcowa produktywność mniejsza od średniej
produktywności – średnia produktywność maleje
Gdy krańcowa produktywność równa zero – produkcja
maksymalna (pochodna!)
Gdy krańcowa produktywność większa od zera –
produkcja rośnie (pochodna!)
Krańcowa produktywność przecina średnią
produktywność w jej maksimum
22
Prawo malejącej produktywności czynników
�
Zwiększając ilość jednego czynnika produkcji i przy
pozostałych czynnikach produkcji na stałym poziomie,
istnieje punkt, powyżej którego krańcowa produktywność
tego czynnika zaczyna maleć
�
�
�
�
24
Początkowo krańcowa produktywność może rosnąć
może b
yć ma
ca, aale
ie mus
musii spa
spadać
dać pon
poniżej
iżej zera
zera!! ((może
być
maleją
lejąca,
le
Nie
całkowita produkcja nadal będzie rosnąć)
Zwykle zachodzi tylko w SR, gdy któryś z czynników stały
(krańcowa produktywność jednego czynnika zależy od ilości
innych czynników)
Np. ilość wypitej kawy a wynik z egzaminu
Zmiany technologii, postęp techniczny
�
�
Zmiany postaci funkcji
Powodują np. przesunięcie całej funkcji produkcji
q
100
C
B
O3
A
O2
50
O1
26
0
1
2
3
4
5
6
7
8
9
10
L
Przy przejściu z A do B
do C, krańcowa
produktywność pracy
moŜe rosnąć
Case study – malejąca krańcowa produktywność
�
�
Thomas Robert Malthus (1766-1834)
Prawo ludności (the principle of population)
�
Liczba ludności nieograniczona
�
�
Produkcja żywności ograniczona
�
�
�
�
28
Wzrost geometryczny
alejąca
M
Male
jąca krańcowa produktywność
Przyrost co najwyżej liniowy
Wynikiem: nędza mas, ubóstwo, głód, klęski żywiołowe, wojny
Zwolennik wstrzemięźliwości seksualnej, późnego zawierania
małżeństw, kontroli urodzeń, ograniczenia pomocy społecznej
Case study –
dlaczego przepowiednie Malthusa się nie sprawdziły?
�
Zmiany technologii
�
�
MPL3 > MPL2
Presja populacyjna + mechanizm rynkowy wymuszają innowacyjność
Substytucja jednych czynników fizycznych innymi
q
MPL2 > MPL1
MPL1
L
30
Case study –
dlaczego przepowiednie Malthusa się nie sprawdziły?
�
�
31
Wzrost kapitałochłonności prowadzi do wzrostu stopy
życiowej i kosztu alternatywnego potomstwa. W krajach
rozwiniętych nastąpił spadek przyrostu naturalnego.
Konwergencja - przepływu kapitału pozwalają na
równywanie poziomów
wyyrównywanie
poziomów żżycia
ycia międz
międzyy kra
krajjami biedn
biednymi
ymi
i bogatymi.
Funkcje produkcji wielu zmiennych – graficznie
q = f ( K, L)
�
�
W LR – oba (wszystkie) czynniki zmienne
Wartość produkcji – w trzecim wymiarze
32
Funkcje produkcji wielu zmiennych – graficznie
33
Funkcje produkcji wielu zmiennych
�
Izokwanty – poziomice produkcji, pokazują wszystkie
kombinacje czynników, które pozwalają efektywnie
wyprodukować tyle samo
E
K 5
4
3
A
B
C
2
q3 = 90
D
1
q2 = 75
q1 = 55
34
1
2
3
4
5
L
Funkcje produkcji wielu zmiennych – graficznie
�
Mapa izokwant jest tożsama z funkcją produkcji
y
x1
54
Substytucja między czynnikami
�
�
�
Jaką kombinację czynników produkcji wybrać?
Można zastąpić jeden czynnik innym i pozostać na tej samej
izokwancie
Techniczna stopa substytucji kapitału przez pracę
(technical rate of substitution)
TRS LK
�
�
ΔK
=
(przy stałej produkcji q )
ΔL
Zawsze ujemna
O ile więcej jednostek pracy potrzeba, aby zastąpić jednostkę
kapitału’
57
Techniczna stopa substytucji
K
5
TRS LK
1
=
ΔK
ΔL
1/4
4
Rezygnacja z kolejnych jednostek K
wymaga zwiększenia L o coraz więcej
1
1/3
TRS maleje wraz ze wzrostem L
(co do wartości bezwzględnej)
3
1
1/2
2
1
1
Q3 =90
1
1
1
58
2
3
3
4
Q2 =75
L
Krańcowa stopa technicznej substytucji
�
‘Zmieniając (krańcowo) ilość jednego czynnika, jak można
zmienić ilość drugiego czynnika, żeby nadal produkować
tyle samo’
�
Np. krańcowa stopa technicznej substytucji pracy przez kapitał
(kolejne jednostki L wymagają zwiększenia K o …)
MRTS KL
�
�
∂f (K , L)
dL
MPK
∂K
=
=−
=−
∂f (K , L)
MPL
dK
∂L
Nachylenie izokwanty (gdy na osi poziomej K, na pionowej L)
Analogiczna do MRS w wyborze konsumenta
60
Krańcowa stopa technicznej substytucji
�
Prawo malejącej MRTS
�
�
�
�
�
Zastępowanie kolejnych jednostek czynnika produkcji
jednostkami innego czynnika daje coraz mniejsze efekty
(wymaga coraz większych wzrostów drugiego czynnika dla
odtworzenia produkcji).
Działa dla wartości bezwzględnej MRTS (maleje po wartościach
dodatnich do zera).
Izokwanty są wypukłe.
Działa jedynie jeśli krańcowe produkcyjności wszystkich
czynników są malejące
Uwaga:
MRTS KL
64
MPK
=−
MPL
MRTS LK
MPL
=−
MPK