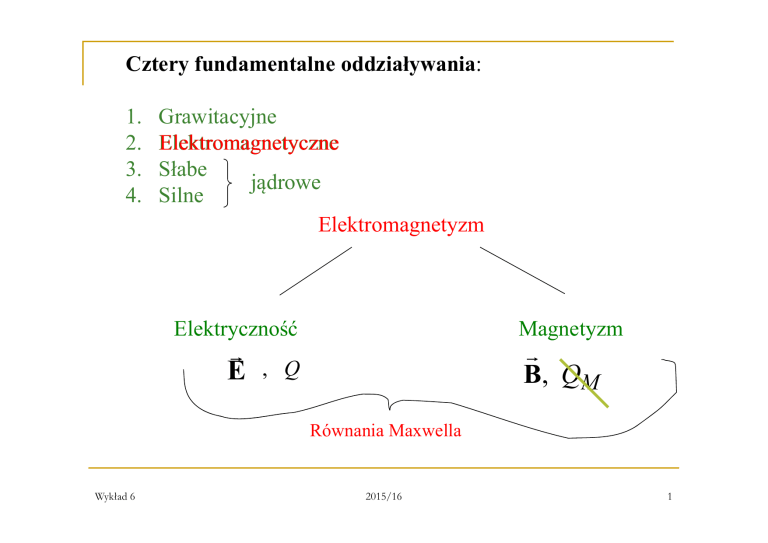
Cztery fundamentalne oddziaływania:
1.
2.
3.
4.
Grawitacyjne
Elektromagnetyczne
Słabe
jądrowe
Silne
Elektromagnetyzm
Elektryczność
r
E
Magnetyzm
r
B, QM
, Q
Równania Maxwella
Wykład 6
2015/16
1
ELEKTROSTATYKA
Wykład 6
2015/16
2
Kwantyzacja ładunku
Każdy elektron ma masę = me i ładunek = -e
p
e=1,602·10-19 C
Każdy proton ma masę = mp i ładunek = e
Ładunek elementarny
Każdy inny ładunek jest wielokrotnością ładunku elementarnego
|Q|= Ne
Wykład 6
2015/16
3
Zasada zachowania ładunku
Całkowity
ładunek
układu
odosobnionego, tzn. algebraiczna
suma
dodatnich
i
ujemnych
ładunków
występujących
w
dowolnej chwili, nie może ulegać
zmianie.
p
Qcałk=const
Qcałk= Qe + Qp
=-e+e
p
Wykład 6
-e
=0
2015/16
4
Przykłady zasady zachowania ładunku
Rozpad promieniotwórczy jądra
238
234
4
92 U → 90 Th + 2 He
Emisja cząstki α
Liczba atomowa Z=92
oznacza 92 protony w
jądrze i ładunek 92e
Z zasady zachowania ładunku
Wykład 6
92e=90e+2e
2015/16
5
Przykłady zasady zachowania ładunku
Proces anihilacji elektronu e- i antycząstki
pozytonu e+
−
+
e +e → γ+γ
Emisja dwóch kwantów promieniowania
elektromagnetycznego
Proces kreacji pary
Wykład 6
−
γ →e +e
2015/16
+
6
Empiryczne prawo Coulomba
r
k q1 q2
1 q1 q2
ˆ
F1, 2 = 2 rˆ1, 2 =
r
1, 2
2
4
πε
r1, 2
o r1, 2
2
1
−12 C
k=
gdzie ε o = 8.85 ⋅10
4 πε o
Nm 2
1785 – waga skręceń
Charles Coulomb 1736-1806
F1,2 = -F2,1
Wykład 6
III zasada dynamiki
2015/16
7
POLE ELEKTROSTATYCZNE A POLE GRAWITACYJNE
PODOBIEŃSTWA
r
F=
r
m1 m 2
F = − G 2 rˆ
r
1 q1 q 2
rˆ
2
4 πε o r
PRAWO COULOMBA
k=
PRAWO NEWTONA
1
= 8,99 ⋅109 N ⋅ m 2 /C 2
4 πε o
G=6,67·10-11 N ·m2/kg2
Oddziaływanie grawitacyjne jest dużo słabsze niż
elektrostatyczne
Wykład 6
2015/16
8
ZASADA SUPERPOZYCJI
r
r
F cał = ∑ Fi
i
FR
qL
FL
q0
qR
oś x
r
r
r
kq 0 (q L − q R )
F 0 = FR + FL =
xˆ
x2
Ładunki qL, q0 i qR są tego samego znaku
Wykład 6
2015/16
9
Zadanie domowe 1-1
Znajdź wartość i kierunek siły wypadkowej działającej na ładunek q0
Wykład 6
2015/16
10
Definicja wektora natężenia pola elektrycznego
E
q
r
r
r F
E=
q0
ładunek próbny q0 >0
Natężenie pola ładunku punktowego
r kq
E = 2 rˆ
r
Natężenie pola pochodzące od wielu ładunków punktowych
(rozkład dyskretny)
r
r
kq
E = ∑ Ei = ∑ rˆi
2
r
i
i i
Wykład 6
2015/16
11
Linie pola – linie równoległe do wektora natężenia pola
Pole ładunku punktowego
Symetria sferyczna
Wykład 6
2015/16
12
Linie pola
Dwa jednoimienne
ładunki punktowe
Wykład 6
2015/16
13
Linie pola
Dipol elektryczny-dwa
różnoimienne ładunki w
bardzo małej odległości
Wykład 6
moment dipolowy
2015/16
14
Zadanie domowe 1-2
(a) Znajdź natężenie pola w punkcie P gdy x > a
(b) Rozważ przypadek graniczny x >> a
Wykład 6
2015/16
15
Ciągły rozkład ładunku
Dla ładunku, dq,
natężenie pola elektrycznego
w punkcie P dane jest
zgodnie z prawem Coulomba
jak dla ładunku punktowego
r kdq
d E = 2 rˆ
r
Dla ładunków dyskretnych pole wypadkowe E jest sumą
r
r
wektorów natężenia Ei czyli
E = ∑E
i
Dla ciągłego rozkładu ładunku
pole wypadkowe jest całką:
Wykład 6
r i
E =
2015/16
∫
r
d E =
∫
Q
kdq
r
2
rˆ
16
Ciągły rozkład ładunku
W zależności od rozkładu ładunku rozróżniamy:
•gęstość liniową ładunku λ,
+
+ + +
+
x
dq
λ=
dx
•gęstość powierzchniową ładunku σ,
+ + +
dS
+
+
dq
σ=
dS
•gęstość objętościową ładunku ρ
dq
ρ=
dV
+
Dla ciągłego rozkładu ładunku, w
zależności od rodzaju gęstości ładunku,
pole wypadkowe może być całką liniową,
powierzchniową lub objętościową:
Wykład 6
2015/16
r
E =
r
∫dE =
∫
V
k ρ dV
rˆ
2
r
17
Przykład 1-1 Liniowy rozkład ładunku
Znaleźć wektor natężenia
pola elektrycznego w
punkcie P na osi liniowego
rozkładu ładunku
Z prawa Coulomba
r
dE x =
kdq
(x − x o )
2
xˆ
Z definicji gęstości liniowej ładunku
dq = λdx
Wykład 6
2015/16
r
k λd x
dE x =
xˆ
2
(x − x o )
18
Wypadkowe natężenie pola jest sumą pól pochodzących od
ładunków elementarnych dq:
L
E = ∫ dE x = ∫
k λdx
2
(x
−
x)
o
0
Wykład 6
kλ L
=
x o (x o − L)
2015/16
19
Zadanie domowe 1-3
Wykazać, że (a) wartość wypadkowego
wektora natężenia pola elektrycznego
na symetralnej pręta od długości L,
naładowanego jednorodnie o
całkowitym ładunku Q wynosi
1
Q
E=
2 πε o y 4 y 2 + L2
(b) Przeprowadzić analizę
otrzymanego wzoru dla L→∞
Wykład 6
2015/16
20
STRUMIEŃ
Φ - szybkość przepływu (powietrza, cieczy)
przez powierzchnię A czyli objętość płynu
przepływającego w jednostce czasu przez
ramkę
A
v
strumień zależy od prędkości
płynu v i orientacji
płaszczyzny ramki
Wykład 6
2015/16
21
WEKTOR POWIERZCHNI
r
A - wektor powierzchni
n̂
- wektor jednostkowy prostopadły do powierzchni
r
A
r
b
Wykład 6
n̂
r
A = Anˆ
Pole powierzchni A
oblicza się zgodnie ze
wzorem na pole
równoległoboku
r r
A = a×b
r
a
2015/16
22
STRUMIEŃ WIELKOŚCI
WEKTOROWEJ
Strumień wielkości
powierzchnię A
r
v
przez
r
r
Φ vr = v o A = vAcos θ
r r
Φ E = E o A = EAcosθ
Strumień pola elektrycznego
r r
ΦE = E o A
pole prędkości
Jednostka 1Nm2/C
Strumień pola magnetycznego
r r
ΦB = B o A
Wykład 6
Jednostka 1 Wb (weber) = 1 T (tesla) m2
2015/16
23
Przypadki szczególne:
gdy θ=0
r
A
Φ vr max = vA
v
gdy θ=π/2
r
A
Wykład 6
v
2015/16
r r
A⊥v
Φ vr = 0
24
STRUMIEŃ POLA ELEKTRYCZNEGO
– definicja
dla dowolnej powierzchni
r
r
ΔΦ Er = E o ΔA
r
r
Φ Er = ∑ E o ΔA
r r
Φ Er = ∫ E o dA
W prawie Gaussa występuje
strumień przez powierzchnię
zamkniętą
Wykład 6
definicja
r r
∫ E o dA
2015/16
25
PRAWO GAUSSA
Dla ładunku punktowego, E~1/r2
Szacujemy strumień
pola przez
powierzchnię kuli ΦE
r
1 Q
Q
2
ΦE = E A =
4π r =
2
4 πε o r
εo
Pole powierzchni kuli A ~ r2
W miarę oddalania się od źródła pola, zwiększa się powierzchnia
A ale maleje E, tak, że strumień pola (EA) pozostaje stały
Wykład 6
2015/16
26
PRAWO GAUSSA
Całkowity strumień pola elektrycznego przez
powierzchnię zamkniętą zależy wyłącznie od ładunku
elektrycznego zawartego wewnątrz tej powierzchni.
Powierzchnię tę nazywamy powierzchnią Gaussa
Q wew
ΦE =
εo
Prawo Gaussa dla pola elektrycznego w postaci całkowej
Jedno z równań Maxwella
r r
Q wew
∫S E o dA = ε o
Wykład 6
2015/16
27
Właściwości powierzchni Gaussa:
•Powierzchnia Gaussa jest tworem hipotetycznym,
matematyczną konstrukcją myślową,
•Jest dowolną powierzchnią zamkniętą, lecz w praktyce
powinna mieć kształt związany w symetrią pola,
•Powierzchnię Gaussa należy tak poprowadzić aby punkt,
w którym obliczamy natężenie pola elektrycznego leżał na
tej powierzchni.
Wykład 6
2015/16
28
Prawo Gaussa stosujemy do obliczania natężenia
pola elektrycznego gdy znamy rozkład ładunku lub
do znajdowania rozkładu ładunku gdy znamy pole.
Prawo Gaussa możemy stosować zawsze ale
sens ma to tylko w tym przypadku gdy pole
elektryczne wykazuje symetrię (sferyczną,
cylindryczną).
Aby skutecznie skorzystać z prawa Gaussa trzeba
coś wiedzieć o polu elektrycznym na wybranej
powierzchni Gaussa.
Korzystając z prawa Gaussa można wykazać
równoważność prawa Gaussa z empirycznym
prawem Coulomba
Wykład 6
2015/16
29
Od prawa Gaussa do prawa Coulomba
dA
r
dA = nˆdA
1. Ładunek punktowy q otaczamy powierzchnią Gaussa – sferą o
promieniu r (dlaczego?).
Bo wiemy, że pole ładunku punktowego ma symetrię sferyczną (A co to
znaczy?)
E II nˆ
cos 0 = 1
E = const. na pow. sfery
2. Obliczamy całkowity strumień przez powierzchnię Gaussa
r
r
ΦE = ∫ E o d A
Wykład 6
2015/16
= ∫ E cosθ dA = ∫ EdA
30
Od prawa Gaussa do prawa Coulomba
r
dA = nˆdA
3. Korzystamy z faktu, że E jest stałe co
do wartości na powierzchni Gaussa
dA
Φ E = E ∫ dA = E(4 πr 2 )
4. Korzystamy z prawa Gaussa
q
ΦE =
εo
5. Porównujemy stronami:
q
E(4 πr ) =
εo
2
q
E(r) =
4 πε o r 2
Prawo Coulomba
Wykład 6
2015/16
31
ZASTOSOWANIA PRAWA GAUSSA
W praktyce zastosowanie prawa Gaussa jest ograniczone do
konkretnych przypadków - symetrii:
a) pole (jednorodne) od naładowanej nieskończonej
płaszczyzny (powierzchniowy rozkład ładunku)
b) pole (o symetrii cylindrycznej) od nieskończenie
długiego pręta (liniowy rozkład ładunku) lub walca
(powierzchniowy rozkład ładunku – walec przewodzący,
objętościowy rozkład ładunku - walec nie przewodzący)
c) pole (o symetrii sferycznej) od naładowanej kuli lub
powierzchni sferycznej
Wykład 6
2015/16
32
JAK KORZYSTAĆ Z PRAWA GAUSSA?
1. Wybrać właściwą powierzchnię Gaussa – dopasowaną do symetrii
rozkładu ładunku. Uzasadnić ten wybór. Wykonać odpowiedni
rysunek
2. Obliczyć strumień pola elektrycznego przez powierzchnię Gaussa
(lewa strona prawa Gaussa).
3. Znaleźć ładunek zawarty wewnątrz powierzchni Gaussa (prawa
strona prawa Gaussa).
4. Porównać obie strony prawa Gaussa wyznaczając wartość wektora
natężenia pola elektrycznego E.
Wykład 6
2015/16
33
Przykład 1-2. Pole elektryczne nieskończonej
powierzchni
Całkowity strumień przez
powierzchnię Gaussa
ΦE = 2 E S
Z prawa Gaussa
Q σS
ΦE =
=
εo εo
Wartość wektora natężenia
pola
σ
E=
2ε o
Wykład 6
2015/16
34
Przykład 1-3. Pole elektryczne liniowego
rozkładu ładunku
Całkowity strumień przez
powierzchnię Gaussa
Φ E = 2 π rhE
Całkowity ładunek zawarty
wewnątrz powierzchni
Gaussa
Q λh
ΦE = =
εo εo
Wartość wektora natężenia pola elektrycznego
λ 1
E=
2 πε o r
Wykład 6
2015/16
symetria cylindryczna
35
Zadanie domowe 1-4.
Bardzo długi walcowy pręt przewodzący o długości L
całkowitym ładunku +q jest otoczony przewodzącą
walcową powłoką (także o długości L)
i całkowitym ładunku -2q (jak na
rysunku). Korzystając z prawa Gaussa,
znajdź: (a) natężenie pola elektrycznego
w punktach na zewnątrz przewodzącej
powłoki, (b) rozkład ładunku na powłoce,
(c) natężenie pola elektrycznego w
obszarze między powłoką i prętem
Wykład 6
2015/16
36
Przykład 1-4. Pole elektryczne sferycznego
rozkładu ładunku – powłoka sferyczna
Całkowity strumień przez powierzchnię
Gaussa będącą sferę o promieniu r
wynosi:
Φ E = 4 π r 2E
Z prawa Gaussa: Φ E =
Q
Q
εo
Ładunek całkowity Q jest rozłożony tylko na
powierzchni sfery o promieniu R
Ze względu na rozkład ładunku rozważmy dwa przypadki:
r>R
Wykład 6
Q
E=
4 πε o r 2
Pole na zewnątrz pustej powłoki
sferycznej jest takie jakby cały
ładunek był skupiony w środku kuli
2015/16
37
Przykład 1-4
cd
r<R
wewnątrz powierzchni
Gaussa tj. sfery o promieniu r
nie ma ładunku
Q
czyli Q=0, ΦE=0 a zatem E=0
Pole wewnątrz naładowanej powłoki sferycznej wynosi zero
Wykład 6
2015/16
38
Rozkład natężenia pola E(r)
dla pustej powłoki sferycznej,
o promieniu R, jednorodnie
naładowanej (Q-ładunek
całkowity)
Wykład 6
2015/16
39
Pole elektryczne przewodnika
Wykład 6
Ładunek znajduje się tylko na powierzchni
przewodnika
Wewnątrz przewodnika Q=0, a zatem E=0
Na powierzchni przewodnika wektor natężenia
pola E jest prostopadły do tej powierzchni
2015/16
40
Pole elektryczne na powierzchni
przewodnika
Całkowity strumień przez
powierzchnię Gaussa
Φ E = EA
Z prawa Gaussa
Q σA
ΦE = =
εo εo
Wartość wektora natężenia pola
σ
E=
εo
Wykład 6
2015/16
41
Związek strumienia z operatorem
dywergencji
Definicja operatora dywergencji
r
div E = lim
r
div E
V→0
r
r
∫EodA
V
jest w granicy nieskończenie małej
objętości V, strumieniem wychodzącym
ze źródła i określa jego wydajność
Twierdzenie Gaussa-Ostrogradskiego
V
r r
r
∫ Eo d A = ∫∫∫divE dV
S
Wykład 6
V
2015/16
42
PRAWO GAUSSA w postaci RÓŻNICZKOWEJ
Korzystamy z twierdzenia Gaussa-Ostrogradskiego:
r
r
r
∫ E o d A = ∫∫∫div E dV
S
V
Z prawa Gaussa w postaci całkowej:
r Qwew 1
r
∫S E o d A = εo = εo
Porównując wyrażenia podcałkowe:
Wykład 6
2015/16
∫∫∫ρdV
V
r ρ
div E =
εo
43
POTENCJAŁ
Wektor natężenia pola –istnieje zawsze
r
r F
Ε=
qo
definicja
Potencjał (skalar) – istnieje tylko dla pól
zachowawczych (potencjalnych)
V=
Wykład 6
Ep
qo
2015/16
definicja
44
Wielkości
charakteryzujące:
siła
r
F
r
F=
energia
potencjalna Ep
natężenie
oddziaływanie
pomiędzy
ładunkami
punktowymi
pole
elektrostatyczne
1 q1 q 2
rˆ
2
4 πε o r
1 q1 q 2
Ep =
4 πε o r
r
r F
Ε=
qo
r
Ε
V=
potencjał V
Wykład 6
2015/16
Ep
qo
45
pole grawitacyjne
Wykład 6
pole elektrostatyczne ładunku ujemnego
2015/16
46
Związek potencjału z natężeniem pola
Dla dowolnej siły zachowawczej, zmiana energii
potencjalnej dEp dana jest:
r r
r r
dE p = −F o d l = −q o E o d l
praca dW
r r
dV = −E o d l
Z definicji potencjału:
dV =
d Ep
qo
b
r r
Vb − Va = − ∫ E o d l
r
E = − grad V
Wykład 6
a
2015/16
47
b
r r
Vb − Va = − ∫ E o d l
a
W
ΔV = Vb − Va = −
qo
Różnica potencjałów ∆V między dwoma punktami jest równa
wziętej z przeciwnym znakiem pracy W wykonanej przez siłę
elektrostatyczną, przy przesunięciu jednostkowego ładunku z
jednego punktu do drugiego.
Różnicę potencjałów nazywamy napięciem U=∆V
Wykład 6
2015/16
48
Jednostki
Na postawie wzoru
V=
Ep
qo
jednostką potencjału jest wolt 1 V = 1 J/C
elektronowolt 1 eV jako jednostka energii w skali atomowej
Jest to energia równa pracy, potrzebnej do przesunięcia
pojedynczego ładunku elementarnego e, na przykład elektronu
lub protonu, między punktami o różnicy potencjałów równej
jednemu woltowi
1 eV= e (1V) = (1,6 ·10-19 C) (1 J/C) = 1,6 ·10-19 J
Na podstawie wzoru
b
r r
Vb − Va = − ∫ E o d l
a
• nowa jednostka natężenia pola elektrycznego 1 V/m
Wykład 6
2015/16
49
Powierzchnie ekwipotencjalnepowierzchnie stałego potencjału
Wykład 6
2015/16
50
Potencjał pola jednorodnego
Va>Vb
a
Potencjał
wyższy Va
b
Potencjał
niższy Vb
d
b
b
b
r r
Vb − Va = − ∫ E o d l = − ∫ Edl = − E ∫ dl = − E (b − a ) = − Ed
a
Wykład 6
a
a
2015/16
51
Potencjał pola ładunku
punktowego
Przesuwamy ładunek próbny qo z punktu P do
nieskończoności
r r
E o d s = E ds cosθ
∞
∞
r r
V∞ − VP = − ∫ E o d s = − ∫ Edr
R
R
E=
1 q
4 πε o r 2
Przyjmujemy V∞=0
V(r) =
Wykład 6
2015/16
1 q
4 πε o r
52
Potencjał dla dyskretnego rozkładu ładunku
Wypadkowy potencjał V układu n ładunków punktowych
qi obliczamy korzystając z zasady superpozycji
n
1
V = ∑ Vi =
4 πε o
i =1
n
qi
∑
i =1 ri
Zadanie domowe 1-5 Na rysunku przedstawiono trzy układy, zawierające
po dwa protony. Uszereguj te układy według wypadkowego potencjału pola,
wytworzonego przez protony w punkcie P, zaczynając od największego.
a.
+
+
Wykład 6
+
b.
+
2015/16
+
c.
+
53
Potencjał ciągłego rozkładu ładunku
Dla naładowanej ładunkiem
powierzchniowym Q powłoki
sferycznej gdy r<R, E=0, czyli
potencjał V jest wielkością stałą,
niezależną od r.
Dla r>R, V zanika z odległością r
jak 1/r
Zadanie domowe 1-6 Pokazać
(obliczając), że potencjał dla
powłoki sferycznej wykazuje
taką zależność V(r) jak na
powyższym wykresie
Wykład 6
2015/16
54
POJEMNOŚĆ
Definicja
Q
C=
ΔV
Jednostką pojemności jest 1F (farad). W praktyce używamy
μF, pF, nF
Analogia między kondensatorem mającym ładunek q i
sztywnym zbiornikiem o objętości V , zawierającym n moli
gazu doskonałego:
V
q = CΔV
n=
p
RT
Przy ustalonej temperaturze T, pojemność kondensatora
C pełni podobną funkcję jak objętość zbiornika
Wykład 6
2015/16
55
Kondensator
Służy do magazynowania energii
Stanowi istotny element obwodu
Linie pola elektrycznego
Wykład 6
2015/16
56
POJEMNOŚĆ KONDENSATORA
PŁASKIEGO
Powierzchnia Gaussa
σ
q
Eo = =
εo εoA
q = Eo εoA
Dla pola jednorodnego pokazaliśmy, że
V = E od
z definicji pojemności
εoA
C=
d
Pojemność zależy tylko od parametrów geometrycznych: A-powierzchni
okładki, d-odległości okładek
Wykład 6
2015/16
57
Przykład 1-5: Jaka musiałaby być powierzchnia okładki
kondensatora płaskiego, aby, przy odległości okładek d=1 mm,
uzyskać pojemność C=1 F?
εoA
C=
d
Cd
A=
εo
1 F⋅10 −3 m
8
2
A=
= 1,13 ⋅10 m
2
−12 2
8,85 ⋅10 C /N⋅ m
mało praktyczne rozwiązanie!!!
Wykład 6
2015/16
58
Zadanie domowe 1-7
Udowodnić, że pojemność kondensatora
cylindrycznego wyraża się wzorem
2 πε o L
C=
ln (R 2 R 1 )
Wykład 6
2015/16
59
Energia zmagazynowana w polu elektrycznym
Praca W wykonana przy ładowaniu
kondensatora zostaje zmagazynowana w
postaci elektrycznej energii potencjalnej
EE, w polu elektrycznym między
okładkami.
Praca elementarna dW wykonana gdy
zostaje przeniesiony dodatkowy ładunek
dq wynosi
q
dW = Vdq = dq
C
q
1 Q2
W = ∫ dW = ∫ dq =
C
2 C
1 Q2 1
1
W = EE =
= QV = CV2
2 C 2
2
Wykład 6
2015/16
60
Gęstość energii
Gęstość energii uE jest to energia potencjalna
przypadająca na jednostkę objętości
EE C V2
uE =
=
Ad 2 Ad
A
C = εo
d
1 ⎛V⎞
u E = εo ⎜ ⎟
2 ⎝d⎠
2
1
2
u E = εoE
2
Wykład 6
2015/16
61
Kondensator w obwodzie
Przykład 1-6: Kondensator o pojemności C=6 μF jest
podłączony do zacisków 9 V baterii. Jaki ładunek
zgromadzi się na okładkach kondensatora?
+
-
C
Q=CV=54 μC
Wykład 6
2015/16
62
Połączenie równoległe kondensatorów
Va − Vb = U1 = U 2 = U
Q1 Q 2 Q
=
= =U
C1 C 2 C
Q = Q1 + Q2 = C1U + C2U = (C1 + C2 )U
C = C1 + C 2
Pojemność kondensatora
zastępczego
Wykład 6
2015/16
63
Połączenie szeregowe kondensatorów
Q Q
U = U1 + U 2 =
+
C1 C2
1 1
1
=
+
C C1 C2
Pojemność kondensatora
zastępczego
Wykład 6
2015/16
64
Zadanie domowe 1-8
(a)
(b)
Wykład 6
Znajdź pojemność zastępczą układu kondensatorów
przedstawionych na rysunku
Znajdź ładunek i spadek potencjału na każdym
kondensatorze jeżeli układ podłączono do baterii 6V.
2015/16
65
PODSUMOWANIE
Elektrostatyka opisuje pola statyczne utworzone przez
ładunki elektryczne w spoczynku.
Pole elektrostatyczne jest zachowawcze (potencjalne).
Pole to jest charakteryzowane przez wektor natężenia
pola i potencjał.
Wartość natężenia pola pochodzącego od konkretnych
rozkładów ładunku obliczamy bądź z zasady
superpozycji i prawa Coulomba bądź z prawa Gaussa.
Kondensator jest urządzeniem, w którym magazynowana
jest potencjalna energia elektrostatyczna. Gęstość
energii zmagazynowanej jest proporcjonalna do
kwadratu pola E.
Prawo Gaussa w postaci całkowej lub różniczkowej
stanowi jedno z równań Maxwella
Wykład 6
2015/16
66