obwody jednofazowe prądu przemiennego

OBWODY JEDNOFAZOWE PRĄDU
PRZEMIENNEGO
mgr inż. Grzegorz Strzeszewski
Zespół Szkół nr 2 w Wyszkowie
2012 r.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
⋆ ⋆ ⋆
Nauka jest dla tych, którzy chcą być mądrzejsi, którzy chcą
wykorzystywać swój umysł do poznawania otaczającego nas
świata.
Jeżeli ktoś chce w życiu pozostać ciemny i głupi, to na takiego
nie ma siły. Musimy mu pozwolić takim zostać.
⋆ ⋆ ⋆
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Klasyfikacja prądów zmiennych
Prąd zmienny
okresowy
nieokresowy
dwukierunkowy
jednokierunkowy
przemienny
pulsujący
sinusoidalnie zmienny
odkształcony
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Przykładowe przebiegi prądów zmiennych
a)
b)
u
c)
u
u
t
0
t
t
0
d)
e)
u
0
π
2
π
3π
2
ωt
2π
f)
u
u
t
0
0
π
2
π
3π
2
ωt
2π
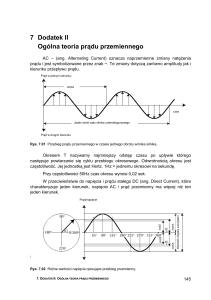
Rysunek: Przebiegi czasowe prądów i napięć zmiennych:
a) bezokresowy jednokierunkowy, b) bezokresowy dwukierunkowy,
c) okresowy, niesymetryczny, d) sinusoidalny (przemienny),
e) dwukierunkowy symetryczny, f) jednokierunkowy pulsujący.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Zasady oznaczania wielkości fizycznych w obwodach
prądu zmiennego
u, i , uR
–
wartości chwilowe napięcia, prądu, spadek
napięcia na rezystorze R (wartość chwilowa),
są to funkcje zależne od czasu;
Im , Um
– wartości maksymalne prądu i napięcia;
I , U, UC – wartości skuteczne prądu, napięcia oraz
spadku napięcia na kondensatorze;
Usr , Isr
– wartości średnie (za pół okresu) napięcia i prądu.
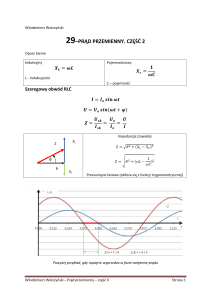
Zależność pomiędzy wartością skuteczną, średnią i maksymalną
prądu i napięcia sinusoidalnie zmiennego:
2
Im
I = √ ≈ 0, 707Im , Isr = Im ≈ 0, 637Im ,
π
2
Um
2
U = √ ≈ 0, 707Um , Usr = Um ≈ 0, 637Um .
π
2
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Wielkości charakteryzujące przebiegi sinusoidalne
Amplituda Am
Faza początkowa Ψ
Okres przebiegu sinusoidalnego T
Pulsacja ω
Częstotliwość f .
u, i
T
T= 1
f
Am
ωt
0
π-ψ
ψ
mgr inż. Grzegorz Strzeszewski
ω = 2πf
2π-ψ
Am
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Wartość średnia prądu sinusoidalnego
Wartością średnią (półokresową) Isr prądu sinusoidalnie
zmiennego o okresie zmienności T i amplitudzie Im nazywamy
średnią arytmetyczną tego prądu obliczoną za połowę okresu, w
którym przebieg jest dodatni.
Podobnie określa się wartość średnią półokresową Usr dla napięcia
sinusoidalnie zmiennego.
Isr = 2 Im ~
0,637Im
π ~
0,637Um
Usr = 2 Um ~
π ~
Dla przebiegów przemiennych wartość średnia całookresowa równa
jest zeru.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Wartość skuteczna prądu sinusoidalnego
Wartością skuteczną prądu sinusoidalnego I nazywamy taką
wartość (równoważnego, zastępczego) natężenia prądu stałego,
który na rezystancji R = const, w czasie równym okresowi T ,
wydzieli tę samą ilość energii cieplnej co dany prąd sinusoidalny.
I =p1 Im ~
~ 0,707Im
2
U =p12 Um ~
~ 0,707Um
Wartość skuteczną napięcia siunusoidalnie zmiennego U
definiujejemy podobnie jak dla prądu.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Przesunięcie fazowe przebiegów sinusoidalnie zmiennych
Przesunięciem fazowym dwóch przebiegów sinusoidalnych
nazywamy różnicę faz początkowych tych przebiegów.
Jeżeli przebiegi czasowe napięć sinusoidalnych wyrazimy jako:
u1 = U1m sin(ωt + Ψ1 ),
u2 = U2m sin(ωt + Ψ2 ),
to przesunięcie fazowe α równe jest:
α = Ψ1 − Ψ2 .
W teorii obwodów elektrycznych istotną rolę odgrywa przesunięcie
fazowe między prądem i napięciem na danym elemencie obwodu
(rezystorze, kondensatorze, cewce). Przesunięcie fazowe prądu
względem napięcia oznaczamy zwykle literą ϕ.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Przesunięcie fazowe między prądem i napięciem
Chwilę, w której rozpoczniemy liczenie czasu t możemy tak
dobrać, aby faza początkowa napięcia Ψ = 0. Wówczas
u = Um sin ωt,
i = Im sin(ωt + ϕ)
gdzie ϕ jest przesunięciem fazowym prądu względem napięcia.
Jeśli ϕ > 0, to prąd wyprzedza napięcie o kąt fazowy ϕ.
Określeniem równoważnym jest stwierdzenie, że napięcie opóźnia
się względem prądu o kąt fazowy ϕ.
Jeśli ϕ < 0, to prąd opóźnia się względem napięcia o kąt fazowy ϕ.
Jest to równoważne ze stwierdzeniem, że napięcie wyprzedza prąd
o kąt fazowy ϕ.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Sposoby przedstawiania przebiegów sinusoidalnych
Przebiegi sinusoidalnie zmienne prądów i napięć można
przedstawiać (opisywać) za pomocą:
wzorów matematycznych,
wykresów czasowych,
wektorów na płaszczyźnie fazowej,
liczb zespolonych.
Przykład opisu napięcia i prądu za pomocą wzorów
matematycznych:
√
u = 230 2 sin 314t,
√
i = 10 2 sin(314t + 300 ).
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Wykresy czasowe przebiegów sinusoidalnych
u, i
u=Um sinωt
i=Im sin(ωt+φ)
φ
0
π
π-φ
φ
2π-φ 2π
ωt
φ
Rysunek: Przesunięcie fazowe ϕ prądu i względem napięcia u na wykresie
czasowym.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Wykresy wektorowe przebiegów sinusoidalnych
u
y
um
u2
u1
Um
u2
u1
Um
ωt3 ωt2
u0
ωt1
u0
ψ
x
Um
u4
Ψ
π -ψ
2
0 ωt1ωt2 ωt3
ωt4
π-ψ
ωt
2π-ψ
u4
Rysunek: Wykres wektorowy i czasowy napięcia sinusoidalnego
u = Um sin(ωt + Ψ).
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Zasady rysowania wykresów metodą nieruchomego
wektora
oś czasu wiruje z prędkością ω = 2πf zgodnie z kierunkiem
wskazówek zegara,
długość wektora jest jego wartością skuteczną,
kąt, jaki tworzy dany wektor z osią czasu (dla t = 0), jest fazą
początkową wektora,
kąt pomiędzy dwoma wektorami równy jest kątowi
przesunięcia fazowego,
kąty przesunięcia fazowego odkłada się w kierunku
przeciwnym do ruchu wskazówek zegara,
dodawanie lub odejmowanie wektorów tych samych wielkości
fizycznych odpowiada dodawaniu lub odejmowaniu przebiegów
sinusoidalnych na wykresie czasowym.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Graficzne dodawanie wektorów
a) Zasada równoległoboku
+
a
=
c=
a
a+
b
b
b
c= a+b
b) Zasada trójkąta
+
a
=
c=
a+
b
a
c= a+b
b
b
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Graficzne odejmowanie wektorów
Wektor przeciwny do danego to wektor mający ten sam kierunek,
taką samą długość i przeciwny zwrot.
-a
a
a,- a wektory przeciwne
Aby od wektora ~a odjąć wektor ~b, należy do wektora ~a dodać
wektor przeciwny do wektora ~b.
-b
=
_
mgr inż. Grzegorz Strzeszewski
a
b
b
c = a-
a
c = a - b = a + (-b)
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Pierwsze prawo Kirchhoffa w obwodach prądu
zmiennego
Pierwsze prawo Kirchhoffa dotyczy bilansu prądów w węźle prądu
zmiennego.
Dla każdego węzła obwodu elektrycznego prądu zmiennego,
suma wartości chwilowych prądu równa jest zeru.
Dla obwodu prądu sinusoidalnie zmiennego (prądu przemiennego),
I prawo Kirchhoffa ma postać.
Suma geometryczna (wektorowa) wektorów natężenia prądów
w węźle równa jest zero.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Drugie prawo Kirchhoffa w obwodach prądu zmiennego
Drugie prawo Kirchhoffa dotyczy bilansu napięć w zamkniętym
oczku obwodu prądu zmiennego.
W dowolnym zamkniętym oczku obwodu prądu zmiennego suma
wartości chwilowych napięć źródłowych i spadków napięć na
elementach R, L, C równa jest zeru.
W obwodach prądu przemiennego II prawo Kirchhoffa ma postać.
Suma geometryczna wektorów sił elektromotorycznych i spadków
napięć w zamkniętym oczku równa jest zero.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik z idealną rezystancją R
b)
a)
i
u
u, i
u=Um sinωt
i=Im sinωt
Um
Im
R
π
0
c)
2π
ωt
I U
φ=0
Kąt przesunięcia fazowego między prądem i napięciem ϕ = 0 (prąd
jest w fazie z napięciem).
Dla wartości skutecznych (także maksymalnych) obowiązuje prawo
Ohma:
U
I = .
R
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik z cewką idealną L
b)
a)
i
u
u, i
u=Um sinωt
Um
Im
L
i=Im sin(ωt- π
2)
π
2
π
0
3π
2
c)
U
2π
ωt
π
φ= 2
I
Definiujemy reaktancję indukcyjną
XL = ωL = 2πfL.
Jednostką reaktancji indukcyjnej jest 1 Ω.
Prawo Ohma dla cewki idealnej:
I =
mgr inż. Grzegorz Strzeszewski
U
.
XL
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik z kondensatorem idealnym C
b)
i
u
u, i
u=Um sinωt
Um
Im
a)
π
2
C
c)
i=Im sin(ωt+π
2)
π
3π
2
0
I
φ= _ π
2
2π
U
ωt
Definiujemy reaktancję pojemnościową
1
1
=
ωC
2πfC
Jednostką reaktancji pojemnościowej jest 1 Ω.
Prawo Ohma dla kondensatora idealnego:
XC =
I =
mgr inż. Grzegorz Strzeszewski
U
.
XC
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Impedancja obwodów szeregowych prądu przemiennego
Impedancja dwójnika szeregowego RLC określona jest jako:
UR
UL
R
L
UC
Z
C
_
X=XL XC
I
φ
U
R
Z trójkąta impedancji mamy:
R = Z cos ϕ, X = Z sin ϕ,
R
X
, tg ϕ = .
Z
R
X = XL − XC – reaktancja obwodu szeregowego.
Jednostką miary impedancji, reaktancji i rezystancji jest 1 Ω.
cos ϕ =
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Admitancja obwodów równoległych prądu przemiennego
Admitancja dwójnika równoległego RLC określona jest jako:
gdzie,
gdzie,
I
U
R
IC
IL
IR
L
Y
C
φ
_
B=BC BL _
G
_
B=BC BL
tgφ = B
G
susceptancja dwójnika równoległego
Jednostką miary admitancji, susceptancji i konduktancji jest
1 simens (S).
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik szeregowy RL
i
R
UR = RI
UL= XLI
uR
u
Impedancja dwójnika szeregowego RL
U
L
uL
U = √UR2 + U2L
Z = √ R2+ X2L
UL
φ>0
I
Prawo Ohma dla prądu przemiennego
UR
I= U
Z
Współczynnik mocy
R
.
Z
Kąt przesunięcia fazowego ϕ w dwójniku RL jest dodatni i należy
do przedziału ϕ ∈ [0, π2 ].
cos ϕ =
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik szeregowy RC
i
UR = RI
UC= XC I
R
uR
u
I UR
φ<0
U = √UR2 + U2C
Impedancja dwójnika szeregowego RC
Z = √ R2+ X2C
C
uC
U
UC
Prawo Ohma dla prądu przemiennego
I= U
Z
Współczynnik mocy
R
.
Z
Kąt przesunięcia fazowego ϕ w dwójniku RC jest ujemny i należy
do przedziału ϕ ∈ [− π2 , 0].
cos ϕ =
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik szeregowy RLC
Impedancja dwójnika szeregowego RLC
i
R
u
L
Z = √ R2+(XL-X C ) 2
uR
Rozpatrujemy trzy przypadki:
UL
UL
uL
U UC
C
u =uR+uL +uC
uC
φ>0
I
I
φ<0
UR
XL >XC
charakter obwodu
indukcyjny
mgr inż. Grzegorz Strzeszewski
UL
UR
UC
φ=0
UC
U
XL <XC
charakter obwodu
pojemnościowy
I U=UR
XL =XC
rezonans
napięć
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik równoległy RLC
Admitancja dwójnika równoleg ego RLC
Y=
i
iR
u
R
L
Rozpatrujemy trzy przypadki:
iC
iL
G2+(BC- BL)2
U
IC
C
I
IR
IL
I
IC
<0
U IR
i = iR + iL + iC
I = IR+ IL+ IC
BC > B L
IC
>0
IL
BC < B L
charakter obwodu charakter obwodu
pojemno ciowy
indukcyjny
mgr inż. Grzegorz Strzeszewski
IL
U I = IR
φ=0
BC = B L
rezonans
prądów
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Moc w obwodach prądu sinusoidalnie zmiennego
Mocą chwilową nazywamy iloczyn wartości chwilowych napięcia i
prądu, czyli
p = ui [W ].
Ponadto w obwodach prądu sinusoidalnie zmiennego wyróżnia się:
moc czynną P = UI cos ϕ, której jednostką jest 1 W (1 wat),
moc bierną Q = UI sin ϕ, której jednostką jest 1 var (1 war),
moc pozorną S = UI , której jednostką jest 1 VA (1
woltoamper).
Związki między mocą czynną, bierną i pozorną:
S=
p
P 2 + Q 2,
P = S cos ϕ,
Q = S sin ϕ.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Trójkąt mocy, współczynnik mocy
a)
b)
P
φ<0
S
Q<0
Q>0
S
φ>0
P
Trójkąt mocy dla odbiornika o charakterze
rezystancyjno - indukcyjnym
Trójkąt mocy dla odbiornika o charakterze
rezystancyjno - pojemnościowym.
Współczynnik mocy
cos ϕ =
mgr inż. Grzegorz Strzeszewski
P
.
S
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Przebieg mocy chwilowej w idealnym dwójniku
rezystancyjnym
u,i ,p
i
p=ui
u
UI
R
UI
ωt
2π
I U
φ=0
i
u
Moc chwilowa dwójnika rezystancyjnego:
p = ui = Um Im sin2 ωt = UI (1 − cos 2ωt).
P = UI , P = I 2 R, P =
mgr inż. Grzegorz Strzeszewski
U2
.
R
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Moc pobierana przez idealny dwójnik rezystancyjny
Rezystor idealny jest elementem, w którym energia elektryczna
przekształcana jest w energię cieplną.
W obwodzie tym nie ma przesunięcia fazowego między prądem i
napięciem (ϕ = 0).
Prąd jest w fazie z napięciem (cos 0 = 1, sin 0 = 0), dlatego
P = UI cos ϕ = UI = S,
Q = UI sin ϕ = 0.
Dwójnik z rezystorem idealnym pobiera tylko moc czynną, moc
bierna jest równa zero.
Moc pozorna
p
S = P 2 + Q 2 = P.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Przebieg mocy chwilowej w cewce idealnej
u, i ,p
i
p
u
L
UI
u
ωt
2π
π
π
2
0
3π
2
U
π
φ= 2
i
I
UI
Moc chwilowa dwójnika z cewką idealną:
π
p = ui = Um Im sin ωt +
sin ωt = UI sin 2ωt.
2
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Moc pobierana przez cewkę idealną
W obwodzie z cewką idealną napięcie wyprzedza prąd o kąt fazowy
ϕ = π2 .
Wiedząc, że cos π2 = 0, sin π2 = 1, otrzymujemy:
P = UI cos ϕ = 0,
Q = UI sin ϕ = UI .
Moc pozorna
S=
p
P 2 + Q 2 = Q.
Dwójnik z cewką idealną nie pobiera ze źródła zasilania mocy
czynnej (P = 0).
Energia pobierana przez cewkę w pierwszej połowie okresu równa
jest energii zwróconej do źródła w drugiej połowie okresu.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Przebieg mocy chwilowej w kondensatorze idealnym
u, i ,p
i
p
u
u
ωt
π
π
2
0
2π
i
Moc chwilowa dwójnika z kondensatorem idealnym:
π
p = ui = Um Im sin ωt −
sin ωt = −UI sin 2ωt.
2
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Moc pobierana przez kondensator idealny
W obwodzie z kondensatorem idealnym napięcie opóźnia się
względem
prądu o kąt fazowy
ϕ = − π2 . Wiedząc, że
cos − π2 = 0, sin − π2 = −1, otrzymujemy:
P = UI cos ϕ = 0,
Q = UI sin ϕ = −UI .
Moc pozorna
S=
p
P 2 + Q 2 = |Q|.
Dwójnik z kondensatorem idealnym nie pobiera ze źródła zasilania
mocy czynnej (P = 0).
Energia pobrana przez kondensator idealny w pierwszej połowie
okresu równa jest energii zwróconej do źródła w drugiej połowie
okresu.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Energia w obwodach prądu przemiennego
W obwodach prądu przemiennego wyróżnia się:
energię czynną, określoną jako:
W = Pt,
której jednostką miary jest dżul (1 J) lub kilowatogodzina
(1 kWh),
energię bierną, określoną jako:
Wb = Qt,
której jednostką jest warosekunda (1 var·s) lub
kilowarogodzina (1 kvarh).
1 kWh = 3, 6 · 106 Ws, 1 kvarh = 3, 6 · 106 var · s.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Kompensacja mocy biernej
Współczynnik mocy odbiorców energii elektrycznej powinien być
bliski jedności (cos ϕ ≈ 1) — wtedy straty mocy czynnej w linii
zasilającej są najmniejsze.
I
odbiornik
I = IO
R
L
C
bateria
kondensatorów
C=
QC
ωU2
mgr inż. Grzegorz Strzeszewski
U
IR
φ1
φ1
IC
IL
IR
U
U
IO
IR
φ2
IO
I
IL
IC
IL
Bateria
kondensatorów
odłączona
I < IO
Bateria
kondensatorów
włączona
QC = P(tg φ1 _ tgφ2)
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Metoda liczb zespolonych
y
b
oś urojona
Liczbę zespoloną można przedstawić jako punkt na płaszczyźnie
zespolonej. Na osiach układu współrzędnych płaszczyzny zespolonej
odkładamy współrzędne punktu będącego obrazem geometrycznym
liczby z; na osi rzeczywistej x liczbę a, zaś na osi urojonej y liczbę b.
z=a+jb
r=√a2+b 2
r
φ
a
jednostka miary na osi : 1
jednostka miary na osi y: j
mgr inż. Grzegorz Strzeszewski
oś rzeczywista
x
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Postacie równowazne liczb zespolonych
Dowolną liczbę zespoloną można przedstawić w trzech
równoważnych postaciach:
algebraicznej
z = a + jb,
trygonometrycznej
z = r (cos ϕ + j sin ϕ),
wykładniczej
z = re jϕ .
gdzie:
r – moduł liczby zespolonej, ϕ – argument liczby zespolonej,
p
b
r = a2 + b 2 , tg ϕ = , e jϕ = cos ϕ + j sin ϕ,
a
a = r cos ϕ, b = r sin ϕ, j 2 = −1.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dodawanie i odejmowanie liczb zespolonych
Suma
liczbą
części
części
dwóch liczb zespolonych z 1 = a1 + jb1 i z 2 = a2 + jb2 jest
zespoloną z 3 , której część rzeczywista jest równa sumie
rzeczywistych liczb z 1 i z 2 , a część urojona równa sumie ich
urojonych, czyli
z 3 = (a1 + a2 ) + j(b1 + b2 ).
Różnica dwóch liczb zespolonych z 1 = a1 + jb1 i z 2 = a2 + jb2 jest
liczbą zespoloną z 4 , której część rzeczywista jest równa różnicy
części rzeczywistych liczb z 1 i z 2 , a część urojona równa różnicy
ich części urojonych, czyli
z 4 = (a1 − a2 ) + j(b1 − b2 ).
Dodawanie i odejmowanie liczb zespolonych odpowiada dodawaniu
i odejmowaniu wektorów na zasadzie równoległoboku.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Mnożenie liczb zespolonych
Iloczyn dwóch liczb zespolonych z 1 = a1 + jb1 = r1 e jϕ1 i
z 2 = a2 + jb2 = r2 e jϕ2 jest liczbą zespoloną z 5 , której moduł
równy jest iloczynowi modułów poszczególnych liczb zespolonych a
argument jest sumą argumentów tych liczb.
z 5 = z 1 z 2 = r1 e jϕ1 r2 e jϕ2 = r1 r2 e j(ϕ1 +ϕ2 ) .
gdzie:
r1 =
q
a12 + b12 , r2 =
tg ϕ1 =
q
a22 + b22 ,
b2
b1
, tg ϕ2 = .
a1
a2
Wiedząc, że j 2 = −1, iloczyn dwóch liczb zespolonych można
przedstawić jako:
z 5 = z 1 z 2 = (a1 + jb1 )(a2 + jb2 ) = (a1 a2 − b1 b2 ) + j(a1 b2 + b1 a2 ).
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dzielenie liczb zespolonych
Dwie liczby zespolone nazywamy sprzężonymi, jeżeli ich moduły są
równe a argumenty są równe co do wartości, lecz mają przeciwne znaki.
z = a + jb = re jϕ ,
z ∗ = a − jb = re −jϕ .
Ilorazem dwóch liczb zespolonych z 1 = a1 + jb1 = r1 e jϕ1 i
z 2 = a2 + jb2 = r2 e jϕ2 jest liczba zespolona, której moduł jest równy
ilorazowi modułów r1 i r2 , a argument jest różnicą argumentów ϕ1 i ϕ2 .
z6 =
r1
r1 e jϕ1
z1
= e j(ϕ1 −ϕ2 ) .
=
jϕ
2
z2
r2 e
r2
Dla postaci algebraicznych liczb z 1 i z 2 :
z6 =
z z∗
(a1 + jb1 )(a2 − jb2 )
a1 a2 + b1 b2
b1 a2 − a1 b2
z1
= 1 2∗ =
=
+j
.
2
2
2
2
z2
z2 z2
a2 + b2
a2 + b2
a22 + b22
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Zasady oznaczania zespolonych wartości skutecznych
Przyjmujemy następujące zasady:
zespolone wartości skuteczne podkreślamy:
U – wartość skuteczna zespolona napięcia,
I – wartość skuteczna zespolona prądu,
Z – impedancja zespolona,
Y – admitancja zespolona.
wartości skuteczne niepodkreślone traktujemy jako moduły
(długości) odpowiednich wielkości zespolonych:
U – moduł wartości skutecznej napięcia zespolonego
I – moduł wartości skutecznej prądu zespolonego,
Z – moduł impedancji zespolonej,
Y – moduł admitancji zespolonej.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik szeregowy RLC (wersja zespolona)
_I
Impedancja zespolona
Moduł impedancji
_
Z=R+j(X
L -XC)
Z = √ R2+(XL-X C ) 2
_R
U
tu
_
U
p
_L
U
_L
U
_C
_ U
U
φ>
_C
U
_I
_R
U
_L
U
_I
φ<0
XL >XC
charakter obwodu
indukcyjny
II prawo Kirchhoffa
:
_L
U
_R
U
_
U
φ=0
_C
U
XL <XC
charakter obwodu
pojemnościowy
_I
_C
U
_ =U
_R
U
XL =XC
rezonans
napięć
Prawo Ohma dla prądu przemiennego
_ R+ U
_ L+U
_C
_ =U
U
mgr inż. Grzegorz Strzeszewski
_I =
_
U
_
_
Z
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dwójnik równoległy RLC (wersja zespolona)
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Schemat zastępczy cewki rzeczywistej – szeregowy
Rezystancja R odwzorowuje rezystancję przewodu,
z którego nawinięto cewkę.
Pojemności międzyzwojowe i pojemności doziemne pominięto.
_I
R
_R
U
_
U
L
_L
U
_
U
_ R+ U
_L
_ =U
U
_ R = R _I
U
_ L = jωL _I
U
_
Z=R+jXL=R+jωL
_L
U
φ>0
_I
_R
U
_
L
tgφ = ω
R
Dobroć cewki rzeczywistej o schemacie zastępczym szeregowym.
_L ω
U
_
L
Q L= UR= R
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Schemat zastępczy kondensatora rzeczywistego –
równoległy
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Postać zespolona mocy pozornej
Moc pozorna S w postaci zespolonej równa jest iloczynowi
napięcia zespolonego U i zespolonego prądu sprzężonego I ∗ :
S = P + jQ, S =
p
P 2 + Q 2.
P = S cos ϕ, Q = S sin ϕ.
Odbiorniki prądu o charakterze indukcyjnym (dla których Q > 0)
pobierają moc bierną z sieci zasilającej.
Odbiorniki prądu o charakterze pojemnościowym (dla których
Q < 0) wysyłają moc bierną |Q| do sieci zasilającej, czyli są
generatorami mocy biernej.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Tylko dla orłów
Na lekcjach matematyki (w szkołach średnich) spotykamy się z
następującymi stwierdzeniami:
Jeśli wyróżnik równania kwadratowego jest ujemny, to
równanie to nie ma rozwiązań.
ax 2 + bx + c = 0, ∆ = b 2 − 4ac < 0 ⇒ brak rozwiązań.
Dla dowolnego kąta x, wartości funkcji trygonometrycznej
cos x zawierają się w przedziale [−1, 1].
−1 ¬ cos x ¬ 1, dla dowolnego x ∈ R.
Znając podstawy liczb zespolonych zastanówmy się, czy na
pewno stwierdzenia te zawsze są prawdziwe? Co będzie, jeśli
zbiór liczb rzeczywistych R rozszerzymy do zbioru liczb
zespolonych C?
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Tylko dla orłów cd 1
Rozważmy równanie kwadratowe o ujemnej delcie:
ax 2 + bx + c = 0; a, b, c ∈ R; x, ∆ ∈ C.
√
√
√
√ √
∆ = b 2 − 4ac = −d, ∆ = −d = −1 d = j d.
| {z }
=j
√
Wstawiając ∆ do znanych wzorów na miejsca zerowe równana
kwadratowego mamy:
√
√
−b − j d
−b − ∆
=
,
x1 =
2
2
√
√
−b + ∆
−b + j d
x2 =
=
.
2
2
Otrzymaliśmy dwa pierwiastki zespolone.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Przykład
Rozwiązać równanie kwadratowe:
x 2 − 2x + 2 = 0.
Rozwiązanie:
a = 1, b = −2, c = 2.
∆ = b 2 − 4ac = (−2)2 − 4 · 1 · 2 = 4 − 8 = −4, delta ujemna!
√
√
√
√
∆ = −4 = −1 · 4 = 2j.
√
−b − ∆
−(−2) − 2j
2 − 2j
x1 =
=
=
= 1 − j,
2
2
2
√
−b + ∆
−(−2) + 2j
2 + 2j
x2 =
=
=
= 1 + j.
2
2
2
Widzimy, że istnieją dwa rozwiązania zespolone tego równania, chociaż
delta jest ujemna.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Tylko dla orłów cd 2
Rozpatrzmy wzór Eulera:
e jx = cos x + j sin x, x ∈ R.
Podobnie, dla ujemnych x mamy:
e −jx = cos x − j sin x.
Dodając stronami powyższe wyrażenia i dzieląc je przez 2, otrzymujemy:
cos x =
e jx + e −jx
.
2
Można udowodnić, że wzór ten jest prawdziwy także dla liczb
zespolonych z ∈ C, czyli
cos z =
mgr inż. Grzegorz Strzeszewski
e jz + e −jz
.
2
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Tylko dla orłów cd 3
Najciekawszym dla nas wnioskiem, wynikającym z poprzednio napisanego
wzoru jest to, że dla kątów czysto urojonych, czyli dla z = jy wartości
przybierane przez funkcję cos jy są liczbami rzeczywistymi, większymi od
jedności.
e y + e −y
cos jy =
∈ R, ∀y ∈ R,
2
cos jy ­ 1 dla kątów jy czysto urojonych.
Można więc powiedzieć, że istnieją kąty (co prawda urojone), dla których
funkcja cos jest większa od jedności. Niektórym osobom (nie tylko
uczniom) wydaje się to zupełnie nieprawdopodobne, wręcz niemożliwe :).
Pytanie dla superorłów: Czy podobne rozumowanie da się przeprowadzić
dla pozostałych funkcji trygonometrycznych: sin, tg, ctg?
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Przykład
Obliczyć cos(j5).
Rozwiązanie:
Wiemy, że
e 5 + e −5
.
2
Korzystając z komputerowego kalkulatora (lub innego), obliczamy:
e 5 ≈ 148, 4131; e −5 ≈ 0, 0067.
Po podstawieniu tych wartości do wzoru, otrzymujemy:
cos(j5) =
cos(j5) ≈
148, 4131 + 0, 0067
= 74, 2099.
2
Otrzymaliśmy więc liczbę rzeczywistą, dużo większą od jedności.
Ogólnie można powiedzieć, że kosinus kąta będącego liczbą urojoną jest
liczbą rzeczywistą, większą od jedności.
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO
Dziękuję za uwagę!
mgr inż. Grzegorz Strzeszewski
OBWODY JEDNOFAZOWE PRĄDU PRZEMIENNEGO