Przewodzenia ciepla

Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME
Wyznaczanie współczynnika przewodzenia ciepła
Cel ćwiczenia
Wyznaczenie współczynnika przewodzenia ciepła materiałów na podstawie pomiarów
strat ciepła przewodu rurowego
Wprowadzenie
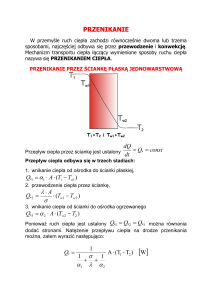
Przepływ gorącego czynnika w rurociągu, np. pary, wiąże się z powstawaniem pewnych strat ciepła do otoczenia. Zapobiegając temu izoluje się przewody odpowiednimi
materiałami o małym współczynniku przewodzenia ciepła, by zwiększyć opór przepływu ciepła od gorącego czynnika, do otoczenia.
Przykładowe materiały termoizolacyjne oraz wpływ temperatury na wartość ich
współczynników przewodzenia przedstawiono w tabeli niżej i na rys. 1.
Rys. 1. Zależność wartości współczynników przewodzenia ciepła dla wybranych
substancji od temperatury
Ze względu na strukturę materiały izolacyjne dzieli się na piankowe (zamknięto-komórkowe i otwarto-komórkowe np. pianki poliuretanowe, polistyrenowe – styropian, spienione szkło, aerożele itp.), włókniste (np. wełny mineralne i szklane) oraz
ziarniste, czyli proszkowe (np. granulowany polistyren, szamot lub perlit – granulat
lawy wulkanicznej, o doskonałych właściwościach cieplnoizolacyjnych i dźwiękochłonnych). Ponadto w kriogenice stosuje się tzw. superizolacje, czyli wielowarstwowe izolacje próżniowe.
Przepływ ciepła jest formą wymiany energii w skali mikro i odbywa się między
obszarami o różnych temperaturach – zawsze od temperatury wyższej do niższej. Są
trzy drogi wymiany ciepła: przewodzenie, konwekcja i promieniowanie.
Przewodzenie ciepła zachodzi w obrębie jednego ciała, w którym istnieją gradienty temperatury. Energia przenoszona jest między cząsteczkami w wyniku ich zderzeń lub poprzez sztywność wiązania. Szybkość rozchodzenia się ciepłą tą drogą wyra1
Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME
ża współczynnik przewodzenia ciepła , którego wymiarem w układzie SI jest W/(m·K).
Definiuje go równanie Fouriera, które dla przepływu ciepła przez płaską ścianę o grubości s ma postać
Q  F  
1   2
s
(1)
gdzie: ̇ – strumień przewodzonego ciepła; F – powierzchnia ścianki (wymiany ciepła);
 – współczynnik przewodzenia ciepła; 1 – temperatura powierzchni zewnętrznej
ścianki, 2 – temperatura powierzchni wewnętrznej ścianki.
Współczynnik przewodzenia ciepła (por tab. wyżej) jest największy dla metali
np. złoto, srebro, miedź a także aluminium  > 200 W/(m·K). Wyjątkowo duży współczynnik ma diament ok. 2000 W/(m·K) oraz grafen   5000 W/(m·K), oba są odmianami węgla (sam grafit ma tylko 140 W/(m·K)). Najmniejsze  < 1 W/(m·K) – mają gazy i izolatory o strukturze porowatej (duży udział gazu, np. styropian 0,045 W/(m·K)).
Wymiana ciepła przez promieniowanie polega na emisji fal elektromagnetycznych (głównie w zakresie 0,4  40 m) przez jedno ciało i pochłanianiu ich przez inne.
Ten sposób wymiany ciepła nie wymaga pośrednictwa substancji, co pozwala na przepływ energii przez próżnię (jak np. ze Słońca do Ziemi). Strumień ciepła między dwiema powierzchniami o temperaturach T1 i T2 jest proporcjonalny do różnicy ich czwartych potęg
̇
(
)
( – stała Stefana-Boltzmana) i zależy od rodzaju materiału; wzajemnego ustawienia,
jakości i kształtu wymieniających ciepło powierzchni. Jego wyznaczenie jest trudne.
Przy niskiej różnicy temperatur jego udział jest stosunkowo mały i dla wygody obliczeń jego wpływ ujmuje się w konwekcji.
Konwekcja (unoszenie) jest to przepływ ciepła, jaki ma miejsce w płynach na
skutek ruchu substancji, podczas którego cząstki o większej energii wewnętrznej (cieplejsze) przepływają do obszarów o mniejszej energii wewnętrznej (zimniejszych)
transportując w ten sposób posiadaną przez siebie energię z jednego miejsca w drugie.
Ruch ten może być wymuszony np. wentylatorem – konwekcja wymuszona lub może
przebiegać na skutek różnicy gęstości (jak przy ogrzewaniu pomieszczeń) – konwekcja
naturalna.
Przepływ ciepła od płynu, w którym zachodzi konwekcja, do ściany nazywa się
przejmowaniem (wnikaniem) ciepła i opisuje go współczynnik przejmowania (wnikania) ciepła , o wymiarze W/(m2·K). Zjawisko wnikania ciepła opisuje prawo Newtona
w postaci:
Q  F    (T   )
(2)
gdzie: T – temperatura czynnika, zaś  – temperaturą ścianki a pozostałe zmienne jak
we wzorze (1). Współczynnik , składa się na ogół z dwóch składowych
   k  r .
(3)
Pierwszy składnik sumy k jest współczynnikiem wnikania ciepła dla czystej konwekcji zaś drugi r jest współczynnikiem uwzględniającym promieniowanie (radiację). Ponieważ, dla małych temperatur jest o pomijalnie mały, stąd zwykle przyjmuje się
 = k.
Wartość współczynnika , zmienia się w bardzo szerokim zakresie i zależy w
dużym stopniu od rodzaju konwekcji (konwekcja naturalna, wymuszona) jak i geome2
Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME
trii przepływu i tak np. dla powietrza atmosferycznego 7,0 
90 W/(m2·K), oliwy 50  700 W/(m2·K), wody 250  10 000
W/(m2·K), cieczy w stanie wrzenia 1600  50 000 W/(m2·K),
a kondensujących się par 3000  100 000 W/(m2·K).
W urządzeniach energetycznych jak np. w wymiennikach ciepła lub przewodach rozprowadzających czynnik
termodynamiczny (parę, gorącą wodę, czynnik chłodniczy)
przepływ ciepła odbywa się od jednego płynu do drugiego
przez pewną przegrodę, a więc kolejno przez etapy: wnikania z płynu do przegrody, przewodzenia w przegrodzie oraz
wnikania z przegrody do płynu (rys.2). Taki proces nazywa
się przenikaniem ciepła, które całościowo opisuje równanie
Peclet’a (4), skonstruowane analogicznie do wzoru Newtona
Rys. 2. Profil temperatury
przy przenikaniu ciepła.
Q  F  k  (T1  T2 ) ,
(4)
gdzie: k – współczynnik przenikania ciepła; T1 – temperatura czynnika grzewczego; T2
– temperatura czynnika chłodzącego a pozostałe zmienne jak we wzorze (1).
W warunkach ustalonej wymiany ciepła miedzy czynnikami oddzielonymi
ścianką ta sama ilość ̇ ciepła jest przejmowana przez ściankę, przewodzona przez nią
i dalej przejmowana przez otoczenie, co uwzględniając równania (1,2,4) można zapisać:
Q  F k (T1  T2 )  F 1 (T1  1 )  F 
1   2
s
 F  2 ( 2  T2 )
(5)
Współczynnik przenikania ciepła k o wymiarze W/(m2K), zwany też współczynnikiem
wymiany ciepła, uwzględnia łącznie wszystkie etapy przepływu ciepła, czyli przewodzenie zdefiniowane prawem Fouriera (1) oraz przejmowanie opisane prawem Newtona (2). Wprowadzając pojęcie oporu właściwego R przenikania ciepła będącego odwrotnością współczynnika R = 1/k wzór (4) można przedstawić w alternatywnej formie
QF
T1  T2 F
 T  F k T
R
R
(6)
Dla przegrody płaskiej wielowarstwowej przy oznaczaniu przez i numeru kolejnej warstwy, opór właściwy przenikania ciepła oblicza się wg wzoru:
R
1
w

i
si
i

1
z
(7)
gdzie nieopisane zmienne to: w i z – współczynniki wnikania ciepła po stronie zewnętrznej i wewnętrznej przegrody; si – grubość i-tej ścianki przegrody; i – współczynnik przewodzenia ciepła i-tej przegrody. We wzorze (7) wyraz pierwszy i ostatni
reprezentują wpływ przejmowania zaś środkowy przewodzenia.
Podczas przepływu czynnika przez zaizolowane rurociągi przewodzenie ciepła
odbywa się przez wielowarstwowe (rurociąg, izolacja, osłona) ścianki cylindryczne. W
tym wypadku wygodniej jest posługiwać się nie strumieniem ciepła ̇ , ale liniową gęstością strumienia ciepła ̇ wyrażoną w W/m czyli strumieniem ciepła przypadającym
na jednostkę długości rurociągu, którą liczy się z analogicznego do (6) ze wzoru
3
Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME
qL 
Q
1
 kL (Tz  Tw ) 
(T  T ) .
L
RL z w
(8)
Tutaj współczynniki kL oraz RL = 1/kL są odpowiednio liniowymi współczynnikami
przenikania ciepła oraz oporu cieplnego, zaś L jest długością odcinka cylindrycznego.
Jeżeli weźmiemy przewód rurowy składający się z n warstw cylindrycznych o
różnym współczynniku przewodzenia ciepła i grubości, indeksowanych (1 .. n) i oznaczymy dla i–tej warstwy współczynnik przewodzenia jako i oraz jej średnice zewnętrzną i wewnętrzną odpowiednio jako di oraz di–1, to wzór – odpowiednik wzoru (7)
– na opór liniowy przegrody cylindrycznej przyjmie postać:
RL 
1
 w d0
n

i 1
1
2i
ln
di
1

di 1  z dn
(9)
Tutaj d0 będzie oznaczało średnicę wewnętrzną przegrody zaś w oraz z współczynniki
przejmowania ciepła wewnątrz i na zewnątrz rurociągu.
Stanowisko pomiarowe i przebieg ćwiczenia
Zasada pomiaru jest oparta o obliczenia wymiennika cieplnego. Wymiennikiem jest
zaizolowany rurociąg, wewnątrz którego przepływa strumień gorącego powietrza.
Wskutek strat ciepła przez izolację powietrze oziębia się oddając ciepło do otoczenia.
Powietrze wokół rurociągu jest w tym przypadku czynnikiem odbierającym ciepło. Zatem wymiana ciepła zachodzi między powietrzem płynącym wewnątrz rurociągu a powietrzem otaczającym przewód. Dokonując pomiaru spadku temperatur między wlotem i wylotem oraz pomiaru temperatur między przegrodami można znając inne parametry przepływu wyliczyć współczynniki przenikania, przewodzenia i przejmowania
ciepła.
Stanowisko pomiarowe to zaizolowany cieplnie przewód rurowy składający się z
rury stalowej (1 warstwa), izolacji piankowej (2 warstwa) oraz osłony z PEHD (3 warstwa). Do rury tłoczone jest gorące powietrze za pomocą elektrycznej nagrzewnicy.
Schemat stanowiska badawczego przedstawiono na rys.3. Skutkiem traconego przez
izolowany rurociąg ciepła jest zmniejszenie się mocy cieplnej czynnika, czego bezpośrednią miarą jest spadek jego temperatury pomiędzy wlotem i wylotem z rurociągu.
Po wygrzaniu się elementów rurociągu i izolacji, w poprzek rurociągu ustala się pewien profil spadku temperatury zgodny z kierunkiem przepływu traconego ciepła
rys.4.
Rys. 3. Schemat stanowiska badawczego: rurociąg żelazny (1), termoizolacja (2), nagrzewnica powietrza
- elektryczna (3), podpory (4), punkty pomiaru temperatury (5): Twe - wlot do ruro-ciągu izolowanego,
Twy – wylot z rurociągu izolowanego
4
Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME
Przed dokonaniem pomiarów, rurociąg gorącego powietrza powinien być wygrzewany
tak długo, aby wymiana ciepła odbywał się w stanie ustalonym. Temperatura powietrza na wlocie powinna wynosić ok. 200C.
Rys. 4. Schemat przenikania ciepła pokazujący profil temperatury przez przekrój
poprzeczny przegrody cylindrycznej wraz
z oznaczeniami wymiarów. Przegroda
składa się z rury stalowej o 1, i grubości
s1, izolacji o 2 i grub. s2 oraz osłony o 3 i
grub. s3. Kropki pokazują punkty pomiaru.
Indeksy przy temperaturach oznaczają: 0 –
środek rurociągu; 1 – pow. wew. rury; 2 –
pow. wew. izolacji; 3 – pow. wew. osłony;
4 – pow. zew. osłony; 5 – otoczenie.
Po osiągnięciu równowagi cieplnej całego układu z otoczeniem, należy w czterech przekrojach rurociągu (oznaczonych literami A–D) dokonać pomiaru (rys. 3):
•
•
•
•
•
•
•
temperatury gorącego czynnika w osi rurociągu T0,
temperatury ścianki wewnętrznej rury stalowej rurociągu T1,
temperatury ścianki zewnętrznej rury stalowej rurociągu T2,
temperatury na zewnątrz izolacji rurociągu T3,
temperatury na zewnątrz osłony rurociągu T4,
temperatury otoczenia T5.
odczytać współrzędne x przekrojów pomiarowych A–D (oznaczania na rys.5)
Rys. 5. Schemat zmiany temperatury
wzdłuż długości (0) czynnikiem
wewnątrz rury, (1..3) na powierzchniach ścianek wew. rury, izolacji i
osłony; (4) na pow. zew. osłony; (5)
powietrzem z otoczenia. Punkty
pomiarowe zlokalizowane są w
przekrojach o współrzędnych xA, xB,
xC oraz xD.
5
Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME
Odczytać z tabliczki znamionowej nagrzewnicy wartość objętościowego strumienia V
gorącego powietrza, zmierzyć długość L i średnice rurociągu D1, D4 oraz grubości przegród.
Obliczenia
Na wykresie należy przedstawić przebieg zmian wzdłuż rurociągu temperatur na powierzchniach (osiach): 0 – centrum rury; 1 – na powierzchni wew. rurociągu; 2 – na
powierzchni wew. izolacji; 3 – na powierzchni wew. osłony; 4 – na powierzchni zew.
osłony oraz 5 – temperatury otoczenia, jak na rys.4.
Należy wyliczyć różnice temperatur w przekrojach wlotowych i wylotowych wybranych odcinków rurociągu (np. między xA a xD) i obliczyć średni logarytmiczny spadek temperatur dla j–tej warstwy pomiędzy punktami pomiarowymi oznaczonymi
znakiem prim (‘) – dla wlotowego oraz znakiem bis (‘’) – dla wylotowego przekroju
odcinka rurociągu ze wzoru:
Tj 
Tj''  Tj'
ln
Tj''
(10)
Tj'
kładąc za j odpowiednio 0,1,2,3 i a za prim i bis temperatury z odpowiednich przekrojów. Na przykład biorąc za odcinek pomiarowy fragment rurociągu między przekrojami A i D należy użyć TA,j w miejsce Tj’ oraz TD,j w miejsce Tj’’. Różnice temperatur T’j
oraz T’’j wyznacza się ze wzorów:
Tj'  Tj'1  Tj'
Tj''  Tj''1  Tj''
(11)
Wyznaczone średnie spadki temperatur Tj będą nam służyć do wyznaczenia współczynników przenikania ciepła, przewodzenia ciepła dla izolacji oraz współczynnika
wnikania ciepła od izolacji do powietrza.
W czasie przepływu powietrza rurociągiem traci on część swojej energii weẇ przez ścianę cylindryczną. Strumień ciepła
nętrznej wskutek przepływy ciepła
stanowi stratę i można go wyznaczyć z bilansu energii, jako różnica pomiędzy strumieniem energii na wlocie Q i wylocie Q '' :
Qstr  Q  Q  V  ( cp )T  To  (  cp )T  To   V    cp  (To  To )


o
o
(12)
gdzie: V – strumień powietrza odczytany z tabl. znamionowej, m3/s;  – gęstość powietrza, kg/m3; cp – ciepło właściwe przy stałym ciśnieniu powietrza, J/(kg K), T0 – temperatury w osi kanału (prim – wlot, bis – wylot)
Parametry powierza (gęstość i ciepło właściwe) należy odczytać z tablic termodynamicznych. Można posłużyć się wzorem dokładnym (pierwsza część 12) i odczytać
wartości cp i  dla konkretnych temperatur w przekroju wlotowym i wylotowym albo
przybliżonym (druga część 12), gdzie cp i  są wartościami średnimi. Teraz ze wzoru (8)
po przekształceniu otrzymujemy wzór na liniowy współczynnik przenikania ciepła kL
przez j–tą przegrodę (rurę, izolację lub osłonę):
6
Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME
Qstr
kL , j 

Tj x  x
''
'


qL
Tj
(13)
gdzie qL  Q / ( x  x) jest liniową stratą ciepła na odcinku od x’’ do x’. Ostatecznie
współczynniki przewodzenia ciepła wyliczymy ze wzorów
kL ,1
1 
dla rury metalowej:
dla izolacji piankowej:
2 
kL ,2
dla materiału osłony:
3 
kL ,3
2
2
2
ln
D3
D2
ln
D4
D3
ln
D2
D1
Natomiast współczynniki wnikania ciepła między powietrzem a rurą:
dla wnikania wewnątrz rury:
w 
dla wnikania na zewnątrz rury:  z 
kL ,0
 D1
k L ,4
 D4
Do obliczeń należy wybrać odcinki AD oraz AB, BC, i CD. Wyliczone dla każdej z tych
odcinków wartości  i  przedstawić w tabeli i wyliczyć średnią dla każdego materiału.
Dla pomiarów wykonanych na rurze niezaizolowanej proszę wykonać jedynie wykres
zmian temperatury i obliczyć straty ciepła na poszczególnych odcinkach i porównać je
ze stratami rurociągu zaizolowanego.
7