Elektrycznoœć i magnetyzm

Dielektryki
Dielektryki – substancje, w których nie występują swobodne nośniki
ładunku elektrycznego (izolatory). Może być w nich wytworzone i
utrzymane bez strat energii pole elektryczne.
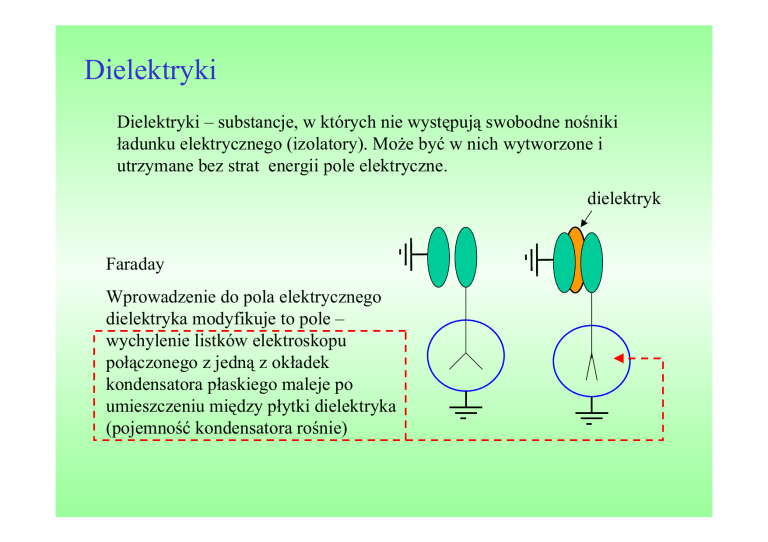
dielektryk
Faraday
Wprowadzenie do pola elektrycznego
dielektryka modyfikuje to pole –
wychylenie listków elektroskopu
połączonego z jedną z okładek
kondensatora płaskiego maleje po
umieszczeniu między płytki dielektryka
(pojemność kondensatora rośnie)
Atom (cząsteczka niepolarna) w polu elektrycznym
E=0
-Ze
W przypadku, kiedy atom (cząsteczka
niepolarna) nie podlega działaniu pola
elektrycznego środki ciężkości ładunku
dodatniego i ujemnego pokrywają się.
Moment dipolowy cząsteczki polarnej jest
równy zeru.
+Ze
_
+
E
_
+
+Ze
_
_
l
-Ze
+
+
Wskutek umieszczenia atomu (cząsteczki
niepolarnej) w polu elektrycznym następuje
przemieszczenie środków ciężkości ładunków
(+Ze i –Ze) co prowadzi do indukowania
momentu dipolowego. Przemieszczenie
rozkładu ładunków prowadzące do
indukowania momentu dipolowego nazywa
się polaryzacją elektronową.
Polaryzacja elektronowa – moment dipolowy
Założenia: kształt, rozmiar i
 ρ = const ,
gęstość „chmury”
ρ =
elektronowej nie zmienia się: 0,
ρ=
r≤a _
r>a
Q
E
a
_
+Ze
4 3
πa
3
_
W warunkach równowagi:
FE = ZeE ,
Z prawa Gaussa:
1 Zel
Eel =
4πε 0 a 3
4πl 2 Eel =
⇒
FE = Fel
ε0
⇒
Fel =
l
_
Fel = ZeEel (l )
Ql
FE
Fel
-Ze
4 3
ρ πl
1 Ql
1
3
Eel =
=
4πε 0 l 2 4πε 0 l 2
1
(Ze )2 l
4πε 0
a3
Polaryzacja elektronowa w gazach
⇒
FE = Fel
ZeE =
1
(Ze )2 l
4πε 0
a3
Stąd:
3
pe = Zel = 4πε 0 a E
α el = 4πa
[α el ] = m
3
3
E
Moment dipolowy indukowany
w cząsteczce niepolarnej pod
wpływem pola elektrycznego E
- polaryzowalność atomu
+
_
pe
r
r
pe = ε 0α el E
Uwaga. Polaryzowalność cząsteczki niepolarnej jest
mniejsza od sumy polaryzowalności tworzących ją atomów.
Jeżeli rozpatrujemy układ w którym koncentracja atomów wynosi N, to
moment dipolowy na jednostkę objętości (polaryzacja P) opisuje równanie:
r
r
r
P = Np = Nαε 0 E
(Zakładając brak oddziaływań
między cząsteczkami (gazy))
Cząsteczki polarne w polu elektrycznym
p
Cząsteczka polarna – całkowity rozkład ładunku cząsteczki ma
moment dipolowy.
r
E =0
Momenty dipolowe poszczególnych
cząsteczek skierowane są we
wszystkich przypadkowych
r
kierunkach.
P=0
r
E≠0
E
Uporządkowanie orientacji momentów
dipolowych cząsteczek, zaburzane
zderzeniami wynikającymi z ruchu
r
termicznego cząsteczek
(+ polaryzacja elektronowa)
P≠0
Dipol w polu elektrycznym.
+q
θ
pe l
-q
E
Na dipol umieszczony w polu elektrycznym działa para sił:
r
r
F = qE
Moment tej pary sił wynosi:
r r
r r r
M = l × F = ql × E
r r r
M = pe × E
gdzie
r r
ql = pe
M = pe E sin θ
Zewnętrzne pole elektryczne E porządkuje momenty dipolowe cząsteczek
polarnych w kierunku zgodnie równoległym z liniami pola.
Energia dipola.
E
+q
θ
pe l
-q
Energia dipola w polu elektrycznym:
E p = qϕ + − qϕ − = q(ϕ + − ϕ − )
ale
l→0
Stąd:
⇒
r r
r r
ϕ + − ϕ − = l ⋅ ∇ϕ = −l ⋅ E
r r
E p = − pe ⋅ E
Polaryzacja zorientowana
Liczba cząsteczek których energia potencjalna wynosi Ep opisuje
rozkład Boltzmana:
 Ep 

n(θ ) = n0 exp −
 kT 
W przypadku niezbyt wysokich pól w temperaturze pokojowej Ep << kT.
Można więc rozwinąć tą funkcję w szereg:
 Ep 
p E cosθ 
 = n0 1 + e
n(θ ) = n0 1 −

kT


 kT 
(Widać, że więcej
cząsteczek ma moment
dipolowy zwrócony
zgodnie z E (cosθ=1) niż
przeciwnie (cosθ=-1))
Gdzie n0 można obliczyć wykonując całkowanie powyższego wzoru po wszystkich kątach
θ, ϕ w wyniku czego otrzymamy całkowitą liczbę cząsteczek w jednostce objętości:
N=
2π
π
0
0
∫ dϕ ∫ n(θ )sin θdθ = 4πn0 ⇒
N
n0 =
4π
Polaryzacja zorientowana w gazach
Polaryzacja równa jest sumie składowych momentów dipolowych
skierowanych wzdłuż pola E:
P = ∑ pe cosθ
Wykonując całkowanie po rozkładzie kątowym:
P=
2π
π
0
0
∫ dϕ ∫ n(θ )pe cosθ ⋅ sin θdθ
P=−
π
N  pe E

+
1
cos
θ

 pe cosθ ⋅ d (cosθ )
∫
2 
kT

0
Stąd:
Npe2 E
P=
3kT
Polaryzacja elektronowa w cieczach
Załóżmy, że ciecz zbudowana jest z cząsteczek niepolarnych, w których pod
wpływem pola E indukuje się moment dipolowy o orientacji zgodnej z
kierunkiem pola. Można przyjąć, że każda cząsteczka, otoczona innymi
cząsteczkami, znajduje się w kulistej wnęce.
r
Ek
r
Ew
r
E
=
Z zasady superpozycji wynika, że:
r r
r
E = E w + Ek
+
Pole elektryczne jednorodnie spolaryzowanej
kuli
Pole jakie wytwarza spolaryzowana kula
jest takie samo jak pojedynczego dipola
umieszczonego w jego środku.
Jeżeli moment dipolowy pojedynczej
cząsteczki wynosi:
+
_
pi = ql
to całkowity moment dipolowy kuli:
4
4
pe = πr 3 Nql = πr 3 P
3
3
E
+ +
+
_
_ _
P
Pole elektryczne jednorodnie
spolaryzowanej kuli
Pole elektryczne jednorodnie spolaryzowanej
kuli c.d.
W dowolnym punkcie na powierzchni kuli potencjał wynosi:
ϕ (r ) =
1
4πε 0
pe cosθ
r2
=
1 4 3 cosθ
πr P 2
4πε 0 3
r
P
P
ϕ (r ) =
r cosθ =
z
3ε 0
3ε 0
Wewnątrz kuli potencjał spełnia r-nie
Laplace,a. Stąd pole wewnątrz kuli:
Jest to również potencjał na
brzegu wnęki.
∂ϕ k
∂ P
= − 
∂z
∂z  3ε 0
r
r
P
Ek = −
3ε 0
Ez = −

z 

Polaryzacja elektronowa w cieczach
Pole wewnątrz wnęki (zgodnie z zasadą superpozycji):
r
r
r P
Ew = E +
3ε 0
Do wzoru
Pole Mossottiego
r
r
r
P = Np = Nαε 0 E
podstawiamy za E pole we wnęce Ew:
r
r
r
r P 

P = Nαε 0 Ew = Nαε 0  E +
3ε 0 

r
P=
r
Nα
ε0E
1 − Nα 3
Polaryzacja w cieczy o
cząsteczkach niepolarnych (r-nie
nie jest słuszne dla cząsteczek
polarnych, np. H2O)
Dielektryki w stałym stanie skupienia
Opis polaryzacji dielektryków w stałym stanie skupienia opiera się na
podobnych zasadach jak w przypadku cieczy, w oparciu o
polaryzowalność elektronową atomów.
W niektórych kryształach występują trwałe momenty dipolowe i ich rotacja
wpływa na polaryzację kryształu.
W kryształach jonowych, np. NaCl występuje polaryzowalność jonowa
związana z przemieszczeniem jonów pod wpływem zewnętrznego pola.
_
+
+
_
+
_
_
+