4
Spis treści
1 Wektory i działania na wektorach
1.1 Dodawanie wektorów . . . . . . .
1.2 Odejmowanie wektorów . . . . . .
1.3 Mnożenie wektora przez liczbę . .
1.4 Iloczyn skalarny wektorów . . . .
1.5 Iloczyn wektorowy wektorów . . .
1.6 Iloczyny wielokrotne . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Kinematyka
2.1 Opis ruchu . . . . . . . . . . . . . . . . . . . . . . .
2.2 Przyspieszenie w ruchu krzywoliniowym . . . . . . .
2.3 Kinematyka ruchu obrotowego . . . . . . . . . . . .
2.4 Opis ruchu w układzie współrzędnych biegunowych
2.5 Całkowanie równań ruchu . . . . . . . . . . . . . .
2.6 Transformacja wektorów prędkości i przyspieszenia
pomiędzy układami odniesienia . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
3
4
5
6
7
.
.
.
.
.
11
11
15
19
22
26
. . . . . . . . . 31
3 Dynamika punktu materialnego
3.1 Zasada bezwładności i transformacja Galileusza . . . . . . . . . .
3.2 II zasada dynamiki Newtona . . . . . . . . . . . . . . . . . . . . .
3.3 Całkowanie drugiego prawa ruchu . . . . . . . . . . . . . . . . . .
3.4 Uogólniona postać II zasady dynamiki i zasada zachowania pędu .
3.5 II zasada dynamiki dla ruchu obrotowego i zasada zachowania momentu pędu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.6 Wzór Bineta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.7 Praca, moc, energia kinetyczna . . . . . . . . . . . . . . . . . . .
3.8 Siły zachowawcze . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.9 Zagadnienie Keplera . . . . . . . . . . . . . . . . . . . . . . . . .
3.10 Prawa Keplera . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.11 Newtonowskie prawo ciążenia powszechnego . . . . . . . . . . . .
.
.
.
.
39
39
41
42
48
.
.
.
.
.
.
.
50
52
54
58
63
69
72
4 Szczególna teoria względności
4.1 Doświadczenie Michelsona - Morleya . . . . . . . . . . .
4.2 Transformacja Lorentza . . . . . . . . . . . . . . . . . .
4.3 Relatywistyczne składanie prędkości . . . . . . . . . . . .
4.4 Efekt aberracji gwiezdnej . . . . . . . . . . . . . . . . . .
4.5 Efekt kontrakcji długości . . . . . . . . . . . . . . . . . .
4.6 Efekt dylatacji czasu . . . . . . . . . . . . . . . . . . . .
4.7 Relatywistyczny efekt Dopplera . . . . . . . . . . . . . .
4.8 Diagramy Minkowskiego . . . . . . . . . . . . . . . . . .
4.9 Efekty relatywistyczne na diagramach Minkowskiego . .
4.10 Transformacja Lorentza jako obrót układu współrzędnych
4.11 Relatywistyczny pęd i moment pędu . . . . . . . . . . .
4.12 Relatywistyczna energia kinetyczna . . . . . . . . . . . .
4.13 Efekt Comptona . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
77
. 78
. 81
. 83
. 85
. 87
. 88
. 89
. 91
. 94
. 96
. 99
. 103
. 106
Rozdział 1
Wektory i działania na wektorach
Wektory to wielkości mające określoną wartość, kierunek i zwrot, oraz podlegające
pewnym regułom algebry wektorów.
Wielkości wektorowe to np. siła, prędkość, przyspieszenie, natężenie pola, itp.
Wielkości, które można jednoznacznie określić za pomocą liczby i jednostki, a
więc mające jedynie wartość, nazywane są skalarami. Skalary podlegają regułom
zwykłej algebry. Wielkości skalarne to np. masa, długość, czas, energia, temperatura, itp. Matematycznie wielkość wektorową opisuje zbiór trzech liczb. Skalar,
matematycznie to jedna liczba.
Wektory znalazły szerokie zastosowanie w fizyce. Dlaczego? Otóż związki pomiędzy wektorami są niezmiennicze względem przesunięć (translacji) i obrotów (rotacji) układu współrzędnych. Notacja wektorowa jest więc idealnym językiem do
wyrażania praw fizyki. Jeżeli prawo możemy przedstawić w postaci równania wektorowego, to zapewniona jest niezmienniczość tego prawa względem obrotów i
przesunięć układu współrzędnych.
1.1
Dodawanie wektorów
Dodawanie wektorów metodą geometryczną
→
− →
−
→
−
Aby znaleźć sumę wektorów A i B należy do końca wektora A dosunąć początek
→
−
→
− →
−
wektora B . Wektor sumy A + B otrzymamy wtedy jako trzeci bok trójkąta (metoda
trójkąta).
2
Wektory i działania na wektorach
Metodą tą można dodawać także większą liczbę wektorów:
Przy dodawaniu wektorów można także posłużyć się ”metodą równoległoboku”.
Dwa wektory zaczepiamy w jednym punkcie i konstruujemy równoległobok. Przekątna tego równoległoboku wyznacza wektor sumy.
B
B
A+B
A
A
Własności dodawania wektorów
→
− →
− →
− →
−
Prawo przemienności: A + B = B + A
→
− →
− →
−
→
− →
− →
−
Prawo łączności: A +( B + C )=( A + B )+ C
Nie jest więc ważne w jakiej kolejności dodajemy wektory i jak je grupujemy.
1.2 Odejmowanie wektorów
3
Dodawanie wektorów metodą analityczną
Metoda analityczna wykorzystuje rozkładanie wektorów na składowe. Dowolny
→
−
wektor A w trójwymiarowym układzie współrzędnych opisują składowe A x , Ay ,
Az , które są długościami rzutów wektora na kierunki osi liczbowych. Wtedy wektor
→
−
A możemy zapisać następująco:
→
−
b
A = Ax xb + Ay yb + Az z,
(1.1)
→
− →
−
A + B = (Ax + Bx )xb + (Ay + By )yb + (Az + Bz )zb
(1.2)
b y,
b zb są wersorami osi liczbowych.
gdzie x,
→
−
→
−
Analitycznie sumę wektorów A =(Ax , Ay , Az ) i B =(Bx , By , Bz ) otrzymamy następująco:
1.2
Odejmowanie wektorów
→
−
Wektor - B definiuje się jako wektor o tej samej długości lecz przeciwnie skierowany
→
−
do danego wektora dodatniego B .
Różnicę dwóch wektorów możemy określić następująco:
→
− →
−
→
−
→
−
A − B = A + (− B )
(1.3)
→
−
co oznacza, że aby znaleźć różnicę wektorów należy dodać wektor - B do wektora
→
−
A.
Odejmowanie wektorów metodą geometryczną
Geometrycznie różnicę dwóch wektorów można znaleźć posługując się metodą
trójkąta.
A
A
B
-B
A-B
-B
4
Wektory i działania na wektorach
→
−
→
−
→
−
Do końca wektora A dosuwamy początek wektora - B . Początek wektora A i
→
−
→
− →
−
koniec - B wyznaczają położenie wektora A - B . Różnicę wektorów można też
przedstawić jako przekątną równoległoboku.
Wektor różnicy wyznacza przekątna równoległoboku rozpięta pomiędzy wierz→
− →
−
chołkami, które wyznaczają końce wektorów A i B . Wektor różnicy skierowany
jest w stronę końca wektora odjemnej.
Odejmowanie wektorów metodą analityczną
Różnicę wektorów wyznaczamy następująco:
→
− →
−
A − B = (Ax − Bx )xb + (Ay − By )yb + (Az − Bz )zb
1.3
(1.4)
Mnożenie wektora przez liczbę
→
−
Iloczyn skalara k i wektora A zapisujemy jako:
→
−
k ·A
(1.5)
Jest to wektor o wartości (długości) k razy większej (jeśli k jest liczbą większą
od 1) lub k razy mniejszej (jeśli k jest ułamkiem mniejszym od 1) od wartości
→
−
→
−
wektora A . Nowy wektor ma taki sam kierunek jak A , a jego zwrot zależy od
tego czy k jest dodatnie czy ujemne. Jeśli k jest liczbą dodatnią to zwrot wektora
→
−
→
−
k· A jest taki sam jak wektora A .
Mnożenie wektora przez liczbę metodą analityczną
→
−
Każdą ze składowych wektora A mnożymy przez k.
→
−
k ·A = kAx xb + kAy yb + kAz zb
(1.6)
1.4 Iloczyn skalarny wektorów
1.4
5
Iloczyn skalarny wektorów
W wyniku skalarnego mnożenia wektorów otrzymujemy liczbę. Wartość iloczynu
→
− →
−
skalarnego wektorów A i B wynosi
→
− →
−
→
− →
−
A · B = A·B cos ^( A , B ),
(1.7)
gdzie A i B to długości wektorów.
Przypadki szczególne
→
− →
−
→
− →
−
→
− →
−
Gdy wektory A i B są równoległe, wtedy A · B = A·B, natomiast gdy A i B są
→
− →
−
antyrównoległe A · B = -A·B.
→
− →
−
→
− →
−
Gdy wektory A i B są prostopadłe, wtedy A · B = 0.
Własności iloczynu skalarnego
→
− →
− →
− →
−
Przemienność: A · B = B · A
→
− →
− →
−
→
− →
− →
− →
−
Rozdzielność iloczynu względem dodawania: A ·( B + C )= A · B + A · C
Iloczyn skalarny w postaci analitycznej
→
− →
−
Iloczyn skalarny wektorów A i B wyznaczamy następująco:
→
− →
−
A · B = A x B x + Ay B y + Az B z .
(1.8)
b
b
b
b
b
Wynika to z faktu, że xb · x=1,
yb · y=1,
zb · z=1.
Natomiast xb · y=0,
xb · z=0
oraz
b
yb · z=0.
W przypadku szczególnym iloczyn skalarny
→
− →
−
A · A = A2 .
(1.9)
Stąd wynika, że długość wektora można otrzymać następująco:
q
r
→
− →
−
A = A · A = A2x + A2y + A2z .
(1.10)
Interpretacja geometryczna iloczynu skalarnego
→
−
→
−
→
−
Jeśli zrzutujemy wektor A na kierunek wektora B to długość rzutu wektora A
→
− →
−
wynosi AB =A cos α, gdzie α = ^( A , B ).
6
Wektory i działania na wektorach
A
α
B
Stąd
AB
→
− →
−
A · B = A · B cos α = B · (A cos α) = B · AB .
(1.11)
→
− →
−
→
−
Zatem iloczyn skalarny wektorów A i B znajdziemy mnożąc długość wektora B
→
−
→
−
przez długość rzutu wektora A na kierunek B .
Obliczenie iloczynu skalarnego wektorów jest więc operacją rzutowania jednego
z wektorów na kierunek drugiego. W przypadku szczególnym rzutowania danego
→
−
wektora A na kierunek osi liczbowej otrzymujemy składową wektora. Na przykład
→
− b
→
−
A ·x=Ax . Składowe wektora A = (Ax , Ay , Az ) można więc wyrazić następująco
→
− b
→
− b
→
− b
Ax = A ·x,
Ay = A ·y,
Az = A ·z.
1.5
Iloczyn wektorowy wektorów
W wyniku wektorowego mnożenia wektorów otrzymujemy wektor. Definicja iloczynu
wektorowego musi zatem określić jego wartość, kierunek i zwrot.
→
− →
−
→
− →
−
Iloczynem wektorowym wektorów A i B nazywamy taki wektor A × B , który
ma następujące własności:
→
− →
−
• Długość wektora A × B wynosi
→
− →
−
→
− →
−
| A × B | = A · B sin ^( A , B ),
•
•
(1.12)
→
− →
−
→
− →
−
gdzie ^( A , B ) oznacza kąt mniejszy zawarty pomiędzy wektorami A i B .
→
− →
−
→
−
→
−
Wektor A × B jest prostopadły zarówno do wektora A jak i B .
→
− →
−
→
− →
−
Wektor A × B tworzy z wektorami A i B układ prawoskrętny (zwrot wektora
→
− →
−
A × B określa reguła śruby prawoskrętnej).
Przypadki szczególne
→
− →
−
→
− →
− →
→
− →
− →
−
−
Gdy wektory A i B są równoległe, wtedy A × B = 0 . Stąd także zachodzi A × A = 0 .
Własności iloczynu wektorowego
1.6 Iloczyny wielokrotne
7
→
− →
− →
− →
−
Brak przemienności: A × B =- B × A
→
− →
− →
−
→
− →
− →
− →
−
Rozdzielność iloczynu względem dodawania: A ×( B + C )= A × B + A × C .
Iloczyn wektorowy w postaci analitycznej
Można go wyrazić w postaci wyznacznika
xb yb zb
→
− →
−
A × B = Ax Ay Az
Bx By Bz
(1.13)
b z,
b y
b × z=
b x,
b zb × x=
b y.
b Natomiast x
b × x=0,
b
b
Wynika to z faktu, że xb × y=
yb × y=0,
b
oraz zb × z=0.
Interpretacja geometryczna iloczynu wektorowego
Interpretację geometryczną ma tylko wartość iloczynu wektorowego. Jest ona równa
polu powierzchni równoległoboku zbudowanego na wektorach.
→
− →
−
Ponieważ wysokość równoległoboku h=A sin ^( A , B ), to pole powierzchni
równoległoboku wynosi:
→
− →
−
→
− →
−
P = B · h = B ·A sin ^( A , B ) = | A × B |
1.6
(1.14)
Iloczyny wielokrotne
Podwójny iloczyn skalarny
Wyznaczanie podwójnego iloczynu skalarnego to w istocie operacja mnożenia wektora przez liczbę
Ważna uwaga:
→
− →
− →
−
→
−
→
− →
−
A · ( B · C ) = k · A , gdzie k = B · C
(1.15)
→
− →
− →
−
→
− →
− →
−
A · ( B · C ) 6= ( A · B ) · C
(1.16)
8
Wektory i działania na wektorach
Podwójny iloczyn wektorowy
→
− →
− →
−
Wektor A ×( B × C ) jest z definicji prostopadły do płaszczyzny wyznaczonej przez
→
− →
− →
−
→
−
wektory A i B × C . Zatem leży on w płaszczyźnie wyznaczonej przez wektory B
→
−
i C.
A
(BxC)
C
B
Ax(BxC)
→
− →
− →
−
→
−
Wektor A ×( B × C ) można więc wyrazić jako kombinację liniową wektorów B i
→
−
C:
→
−
→
− →
−
→
−
→
−
A × ( B × C ) = λ B + µ C − prawo rozwinięcia.
(1.17)
Dokładnie obliczenia pokazują, że
→
− →
−
→
− →
−
λ = A · C , µ = −A · B
(1.18)
→
−
→
− →
−
→
− →
− →
−
→
− →
− →
−
A × (B × C ) = ( A · C ) · B − ( A · B ) · C
(1.19)
Zatem ostatecznie:
Iloczyn mieszany
→
− →
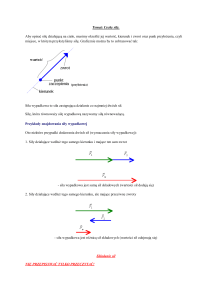
− →
−
Iloczyn mieszany ( A × B )· C jest liczbą. Przyjmuje on wartości dodatnie lub
ujemne w zależności od tego czy kąt α zawarty pomiędzy kierunkami wektorów
→
− →
− →
−
A × B i C jest kątem ostrym czy rozwartym.
Wartość iloczynu mieszanego ma prostą interpretację geometryczną. Objętość
→
− →
− →
−
równoległościanu zbudowanego na wektorach A , B , C jest równa wartości iloczynu
→
− →
− →
−
mieszanego ( A × B )· C .
a
h
C
B
A
1.6 Iloczyny wielokrotne
9
Objętość równoległościanu znajdziemy mnożąc pole powierzchni jego podstawy
→
− →
−
| A × B | przez wysokość h. Zatem
→
− →
−
→
− →
−
→
− →
− →
−
V = | A × B | · h = | A × B | · C · cos α = ( A × B ) · C
(1.20)
Z interpretacji geometrycznej wynika ważna własność iloczynu mieszanego →
− →
− →
−
jeśli iloczyn mieszany znika, oznacza to, że wektory A , B i C leżą w jednej
płaszczyźnie.
Ponadto, ponieważ każdą ścianę równoległościanu możemy uważać za podstawę
mamy:
→
− →
− →
−
→
− →
− →
−
→
− →
− →
−
( A × B ) · C = (B × C ) · A = (C × A) · B .
(1.21)
→
− →
− →
−
→
− →
− →
−
( A × B ) · C = A · ( B × C ).
(1.22)
Możliwa jest więc cykliczna zamiana wektorów.
Inna własność iloczynu mieszanego:
Zachowując kolejność wektorów można zamienić mnożenie wektorowe na skalarne
i odwrotnie.
Iloczyn mieszany wyliczamy wyznaczając wartość wyznacznika:
Ax Ay Az
→
− →
− →
−
( A × B ) · C = Bx By Bz .
Cx Cy Cz
(1.23)
10
Wektory i działania na wektorach
Rozdział 2
Kinematyka
2.1
Opis ruchu
Zajmować się będziemy w tym rozdziale opisem ruchu ciała, które możemy traktować jako obiekt punktowy. Takie przybliżenie możemy stosować w tych zagadnieniach ruchu, w których możliwe jest zaniedbywanie rozmiarów ciał. Ciało punktowe możemy traktować jako model matematyczny rzeczywistego ciała materialnego (może to być zarówno obiekt tak mały jak np. elektron, ale także ogromna
planeta) jako jego idealizację, pozwalającą na prosty opis matematyczny wielu
sytuacji fizycznych.
Układ odniesienia
Wszelkie ruchy ciał występujące w przyrodzie, są to ruchy względne. Mówimy, że
jakieś ciało jest w ruchu, jeżeli jego położenie względem innego wybranego ciała lub
układu ciał zmienia się wraz z upływem czasu. Ciało, które uważamy za poruszające się, porusza się względem innego ciała (czy też układu ciał), które uważamy za
nieruchome. To nieruchome ciało (czy też ciała) stanowią układ odniesienia, względem którego odbywa się ruch. Jeżeli rozważane ciało nie zmienia swojego położenia
względem układu odniesienia , to mówimy, że jest ono w spoczynku względem tego
układu. Tak więc wybór układu odniesienia jest warunkiem koniecznym, jaki musi
być spełniony, aby można było opisywać ruch lub spoczynek.
Układ odniesienia, w różnych przypadkach można wybrać różnie. Zwykle wybiera
się go w taki sposób, aby opis ruchu był możliwie prosty i jak najbardziej naturalny. Z ciałami stanowiącymi wybrany przez nas układ odniesienia wiążemy
pewien układ współrzędnych np. układ współrzędnych kartezjańskich, sferycznych
czy cylindrycznych. Oczywiście opis ruchu ciała w różnych układach odniesienia
będzie różny. Przejście od opisu ruchu w jednym układzie odniesienia do opisu
12
Kinematyka
ruchu w innym układzie odniesienia jest możliwy dzięki przekształceniom matematycznym - transformacjom współrzędnych.
Wektor położenia, równanie ruchu i tor ruchu
Położenie ciała w danym układzie współrzędnych opisujemy przy pomocy wektora
→
−
r zwanego wektorem położenia, wektorem wodzącym czy też promieniem wodzącym. Jest to wektor zaczepiony w początku układu współrzędnych, którego koniec
−
wskazuje aktualne położenie ciała. Wektor →
r jest funkcją swoich współrzędnych.
→
−
−
W układzie współrzędnych kartezjańskich r =→
r (x,y,z).
−
−
W układzie współrzędnych sferycznych →
r =→
r (r,θ, ϕ). Wektor jest określony
poprzez podanie promienia sfery, na której znajduje się punkt oraz dwóch kątów
θ i ϕ.
z
θ
r
φ
y
x
−
−
W układzie współrzędnych cylindrycznych →
r =→
r (ρ,ϕ,h) . Wektor jest określony
poprzez podanie promienia cylindra ρ, na powierzchni którego znajduje się punkt
oraz kąta biegunowego ϕ i wysokości h.
z
ρ
r
φ
h
y
x
Jeśli ciało punktowe znajduje się w ruchu to wektor położenia zmienia się w
−
−
−
−
czasie →
r =→
r (t). Zależności →
r =→
r (t) jest wektorowym równaniem ruchu. Rów-
2.1 Opis ruchu
13
naniu temu w układzie współrzędnych kartezjańskich odpowiadają trzy skalarne
równania ruchu:
x = x(t),
y = y(t),
z = z(t)
(2.1)
Krzywą geometryczną, którą zakreśla punkt podczas swojego ruchu nazywamy
torem ruchu. Skalarne równania ruchu są zarazem równaniami parametrycznymi
toru z parametrem t. Rugując z równań ruchu czas t otrzymujemy równanie toru.
Dla ruchu płaskiego równanie ruchu to:
x = x(t),
y = y(t)
(2.2)
Po wyrugowaniu czasu t otrzymamy równanie
y = f (x),
(2.3)
które jest równaniem krzywej geometrycznej, po której porusza się cząstka.
Prędkość ciała i droga
−
Prędkością ciała →
v nazywamy wektor dany przez pierwszą pochodną wektora
−
położenia →
r (t) względem czasu t:
−
d→
r
→
−
−̇
v =
=→
r
(2.4)
dt
Zapis pierwszej pochodnej w postaci kropki pochodzi od Newtona i dotyczy tylko
−
różniczkowania po czasie. Składowe wektora prędkości →
v =(vx , vy , vz ) wyrażają się
następująco:
vx = ẋ,
vy = ẏ,
vz = ż.
(2.5)
Długość wektora prędkości to szybkość
r
−
v = |→
v | = vx2 + vy2 + vz2
(2.6)
Szybkość jest więc wielkością skalarną. Możemy więc zapisać:
→
−
b
v = v · t,
b = 1
|t|
(2.7)
14
Kinematyka
Wektor tb jest zawsze skierowany w kierunku wektora prędkości; jest wektorem
jednostkowym stycznym do toru ruchu.
Drogą ciała s w danym przedziale czasu nazywamy długość łuku, którą ciało
zakreśla podczas ruchu. Droga jest więc wielkością skalarną.
W przedziale czasu od chwili t1 do t2 =t1 +dt (dt oznacza nieskończenie mały
przyrost czasu) ciało pokonuje drogę ds.
Jeśli przyrosty są nieskończenie małe to:
−
|d→
r | = ds
−
b Stąd wynika definicja wersora stycznego t:
b
Zatem d→
r = ds · t.
−
d→
r
tb =
ds
(2.8)
(2.9)
oraz także
−
−
d→
r
d→
r ds ds b
→
−
v =
=
·
=
· t = v · tb
dt
ds dt
dt
Szybkość zatem jest pierwszą pochodną drogi względem czasu t:
v=
ds
dt
(2.10)
(2.11)
Stąd ponieważ ds= vdt widać, że drogę s w przedziale czasu (t 1 , t2) możemy znaleźć
jako wartość całki:
Z t
2
s=
vdt
(2.12)
t1
Wyznaczanie całki oznacza obliczanie pola powierzchni pod krzywą na wykresie
zależności szybkości od czasu. Wartość całki jest równa zakreślonemu na rysunku
poniżej polu powierzchni.
2.2 Przyspieszenie w ruchu krzywoliniowym
15
V
S
t1
t2
t
Przyspieszenie
Przyspieszenie ciała to wektor dany przez pierwszą pochodną wektora prędkości
względem czasu t:
−
−
d→
v
d2 →
r
→
−
a =
=
(2.13)
dt
dt2
Rozpisując na składowe:
→
−
a = ax xb + ay yb + az zb
ax = v̇x = ẍ, ay = v̇y = ÿ, az = v̇z = z̈
2.2
(2.14)
Przyspieszenie w ruchu krzywoliniowym
W ogólnym przypadku ruchu krzywoliniowego zarówno kierunek wersora tb jak i
wartość wektora prędkości są zmienne w czasie:
−
d→
v
d
→
−
b
a =
= (v · t).
dt
dt
(2.15)
dtb
dv
→
−
a = v + tb
dt
dt
(2.16)
Traktując formalnie powyższe wyrażenie jako pochodną iloczynu mamy:
Pierwszy człon tego wyrażenia bierze pod uwagę zmianę kierunku wektora prędkości, drugi człon wynika ze zmiany wartości wektora prędkości w czasie. Widać
więc, że w ruchu krzywoliniowym istnieje zawsze różne od zera przyspieszenie,
nawet jeśli wartość prędkości jest stała i dv
dt = 0.
Pokażemy teraz, że
dtb v
= nb
(2.17)
dt ρ
gdzie ρ jest promieniem krzywizny toru krzywoliniowego, a nb jest wersorem norb
malnym (prostopadłym) do kierunku wersora tb (nb · t=0)
.
16
Kinematyka
Równanie (2.17) jest wyrażeniem wektorowym. Najpierw jednak posługując się
konstrukcją geometryczną pokażemy, że dla ruchu po okręgu zachodzi następujący
związek skalarny
1
b = ds
|dt|
(2.18)
ρ
Z podobieństwa trójkątów równoramiennych AOB i DBC przedstawionych na
rysunku wynika:
b
ds |dt|
= b ,
ρ
|t|
b = 1, mamy:
gdzie ρ jest promieniem okręgu. Ponieważ |t|
1
b = ds.
|dt|
ρ
(2.19)
(2.20)
Aby wykazać zależność wektorową (2.17) musimy najpierw udowodnić proste twierdzenie matematyczne, które przyda się także w dalszych rozważaniach:
Jeśli wektor ma stałą długość, to jego przyrost jest do niego prostopadły.
→
− →
−
Dla wektora A = A (q) (tzn. takiego, który jest funkcją pewnego parametru q),
→
−
dla którego | A | = const, na podstawie wyrażonego twierdzenia zachodzi:
→
−
→
− dA
A·
=0
dq
(2.21)
Dowód twierdzenia jest bardzo prosty.
→
−
→
−
Jeśli | A | = const., to także | A |2 = const. Zatem
→
−
d→
−2
→
− dA
0=
A (q) = 2 A ·
dq
dq
A stąd otrzymujemy wyrażenie (2.21).
(2.22)
2.2 Przyspieszenie w ruchu krzywoliniowym
17
Po tej dygresji matematycznej wracając do naszych rozważań z kinematyki
ruchu krzywoliniowego mamy:
dtb
tb ·
= 0.
(2.23)
dt
b
dt
Zatem kierunki wektorów tb i dt
są wzajemnie prostopadłe. Wobec tego kierunek
db
t
b
wektora dt
jest zgodny z kierunkiem wersora n.
Ze związku skalarnego
1
b = ds.
(2.24)
|dt|
ρ
Otrzymujemy zatem związek wektorowy:
dtb 1 ds
v
=
nb = nb
dt ρ dt
ρ
(2.25)
Przeprowadzone tutaj wyprowadzenie zależności (2.17) przedstawiono dla szczególnego przypadku ruchu po okręgu, ale zależność (2.17) jest prawdziwa dla każdego
ruchu krzywoliniowego. W pełni formalnie wyprowadzenie zależności (2.17) można
znaleźć w podręcznikach geometrii różniczkowej (tzw. wzór Freneta).
Reasumując, w ruchu krzywoliniowym przyspieszenie składa się z dwóch wkładów
→
−
b
a = at tb + an n,
(2.26)
at to wartość przyspieszenia stycznego, an to przyspieszenie normalne (dośrodkowe), gdzie:
at = v̇ = s̈
v2
an =
.
(2.27)
ρ
→
−
−
Przyspieszenie styczne →
a t jest skierowane tak jak wersor tb = ddsr , a jego zwrot
−
b dla
zależy od znaku pochodnej v̇. Dla v̇ > 0 mamy ruch przyspieszony →
a t = at t,
b
v̇ < 0 mamy ruch opóźniony ab t = −at t.
−
−
b
Przyspieszenie normalne →
a n ma zawsze zwrot wersora nb (→
a n = an n),
bo za2
v
wsze an = ρ ­ 0. Przyspieszenie normalne działa wzdłuż promienia krzywizny
toru i jest zawsze skierowane do środka krzywizny toru. Stąd jego druga nazwa
przyspieszenie dośrodkowe.
at
a
an
o
18
Kinematyka
Przykład - przyspieszenie w ruchu po okręgu
Dany jest ruch:
x(t) = ρ cos ωt
y(t) = ρ sin ωt,
(2.28)
gdzie ρ i ω to stałe. Wektor położenia ma postać:
→
−
r (t) = ρ(xb cos ωt + yb sin ωt).
(2.29)
−
|→
r | = ρ.
(2.30)
Łatwo sprawdzić, że długość tego wektora jest stała w czasie
Tor ruchu znajdziemy jeśli z równań ruchu (2.28) wyrugujemy czas. Otrzymamy
wtedy:
x2 + y 2 = ρ 2 .
(2.31)
Jest to równanie okręgu o środku w początku układu współrzędnych i promieniu
równym ρ.
Znajdźmy prędkość:
ẋ(t) = −ωρ sin ωt
ẏ(t) = ωρ cos ωt
→
−
v = ωρ(−xb sin ωt + yb cos ωt).
(2.32)
Długość tego wektora jest także stała
−
|→
v | = ωρ.
(2.33)
Ponadto, łatwo sprawdzić, że iloczyn skalarny wektorów
→
−
−
v ·→
r =0
(2.34)
Oznacza to, że w czasie ruchu oba wektory pozostają cały czas wzajemnie prostopadłe.
Przyspieszenie w tym ruchu:
ẍ(t) = −ω 2ρ cos ωt
ÿ(t) = −ω 2ρ sin ωt
→
−
−
a = −ω 2 ρ(xb cos ωt + yb sin ωt) = −ω 2→
r.
(2.35)
Wartość przyspieszenia:
−
|→
a | = ω2ρ
(2.36)
2.3 Kinematyka ruchu obrotowego
19
nie zmienia się więc w czasie ruchu. Można także pokazać, że iloczyn wektorowy
→
−
−
a ×→
r = 0.
(2.37)
Oznacza to, że w czasie ruchu wektor przyspieszenia jest skierowany wzdłuż kierunku
−
wektora →
r . Potwierdza to analiza rozkładu przyspieszenia na składowe styczną i
normalną - przyspieszenie styczne jest równe 0, całe przyspieszenie ma kierunek
przyspieszenia normalnego (dośrodkowego):
at = v̇ = 0
v2
= ω 2 ρ.
an =
ρ
(2.38)
Widać więc, że równania ruchu (2.28) opisują ruch jednostajny po okręgu o promieniu ρ .
2.3
Kinematyka ruchu obrotowego
Do opisu ruchu obrotowego wprowadza się dodatkowe specyficzne dla tego ruchu
wielkości fizyczne.
Prędkość kątowa
−
Najpierw zdefiniujemy wektor nieskończenie małego obrotu wektora położenia d →
ϕ.
−
Obrotowi o kąt dϕ wektora położenia przypisujemy wektor d→
ϕ skierowany
wzdłuż osi obrotu o zwrocie zgodnym z regułą śruby prawoskrętnej (patrz rysunek
powyżej). Wielkość
−
d→
ϕ
→
−
ω =
dt
(2.39)
nazywamy prędkością kątową. Używając pojęcia szybkości kątowej ω = ϕ̇ możemy
−
zapisać →
ω = ϕ̇ωb 0 , gdzie ωb 0 jest wersorem, którego kierunek i zwrot jest zgodny z
−
kierunkiem i zwrotem wektora d→
ϕ.
20
Kinematyka
Wyprowadzimy teraz dla przykładu ruchu po okręgu związek łączący prędkość
−
−
kątową →
ω i liniową →
v.
Najpierw korzystając z definicji kąta w mierze łukowej możemy wyprowadzić
związek skalarny v = ω r. Według tej definicji kąt dϕ otrzymujemy ze stosunku
długości łuku ds do promienia r; dϕ = ds
r .
Stąd ponieważ ds = r dϕ otrzymujemy
dϕ
ds
=r
= r ω.
(2.40)
dt
dt
−
Ponadto z definicji wynika, że →
ω jest wektorem prostopadłym do płaszczyzny
−
−
−
ruchu (→
ω ⊥→
v ). Ponieważ w ruchu po okręgu |→
r | = const., zatem z twierdzenia,
→
−
−
które niedawno udowodniliśmy wynika, że iloczyn skalarny →
r · ddtr = 0. Stąd
−
−
widać, że cały czas w czasie ruchu wektor →
v jest prostopadły do →
r . Związek
→
−
→
−
pomiędzy wektorami ω i v jest wobec tego następujący:
v=
→
−
−
−
v =→
ω ×→
r
(2.41)
Przyspieszenie kątowe
Zróżniczkujmy po czasie obie strony wyrażenia (2.41). Otrzymamy wtedy
−
−
−
d→
v
d→
r
d→
ω
→
−
−
= ω ×
+
×→
r
dt
dt
dt
(2.42)
→
−
−
−
−
−
a =→
ω ×→
v +→
ε ×→
r,
(2.43)
lub
gdzie wprowadziliśmy oznaczenie
−
d→
ω
→
−
ε =
.
dt
(2.44)
−
Nowa wielkość fizyczna →
ε , która pojawiła się w tym wyrażeniu to przyspieszenie
kątowe.
2.3 Kinematyka ruchu obrotowego
21
Pierwszy człon po prawej stronie wyrażenia (2.43) to przyspieszenie normalne:
→
−
−
−
−
−
−
−
−
−
−
−
−
ω ×→
v =→
ω × (→
ω ×→
r ) = (→
ω ·→
r )→
ω − (→
ω ·→
ω )→
r = −ω 2→
r
(2.45)
→
−
−
−
a =→
an+→
a t,
(2.46)
−
−
−
Występujący w tym wyrażeniu iloczyn skalarny →
ω ·→
r = 0, ponieważ wektory →
ω
−
−
i→
r w czasie ruchu są do siebie prostopadłe. Wynika to z definicji →
ω . Wyrażenie (2.43) to w istocie zatem rozkład na dwa wektory wzajemnie prostopadłe przyspieszenie styczne i normalne:
−
−
−
−
−
gdzie →
a n = −ω 2 →
r oraz →
at=→
ε ×→
r.
−
Występujący w wyrażeniu na przyspieszenie styczne wektor →
ε ma kierunek
zmian prędkości kątowej. Zmiany te mogą być związane zarówno ze zmianami
−
wartości jak i kierunku →
ω . Ilustruje to następująca analiza:
d
dω
dωb 0
→
−
ε = (ωb 0 ω) = ωb 0
+ω
.
dt
dt
dt
−
Dla ruchu płaskiego nie ma zmian kierunku wektora →
ω w czasie;
(2.47)
= 0. W takim
−
przypadku przyspieszenie kątowe wynika wyłącznie ze zmian wartości wektora →
ω.
→
−
ε = ωb 0 ω̇
db
ω0
dt
(2.48)
−
Widać stąd, że w ruchu płaskim wektor →
ε ma zawsze kierunek osi obrotu; zwrot
→
−
wektora ε zależy, od tego czy prędkość kątowa rośnie czy maleje w czasie. Kiedy
−
−
ω̇ > 0, wtedy →
ε = εωb 0 . Kiedy ω̇ < 0, wtedy →
ε = −εωb 0 .
Prędkość polowa
W czasie nieskończenie małego obrotu wektor położenia zakreśla także pole powierzchni
→
−
dΣ. Temu polu powierzchni można przypisać wektor d Σ skierowany wzdłuż osi
obrotu i o zwrocie zgodnym z regułą śruby prawoskrętnej.
Z definicji iloczynu wektorowego wynika, że zakreślone pole powierzchni ma
wartość równą długości wektora
1 − →
→
−
d Σ = (→
r ×−
r 0 ).
2
(2.49)
22
Kinematyka
−
→
−
−
−
Ponieważ →
r0=→
r + d→
r , to wektor dΣ można też zapisać następująco
1 − →
1 −
→
−
−
−
−
r ×−
r +→
r × d→
r 0 ) = (→
r × d→
r ),
d Σ = (→
2
2
−
−
bo →
r ×→
r = 0.
−
Definicja prędkości polowej →
σ jest następująca:
→
−
d
Σ
→
−
σ =
.
dt
(2.50)
(2.51)
Z zależności (2.50) wynika:
−
1 →
d→
r
1− →
→
−
−
σ = (r ×
)= →
r ×−
v
(2.52)
2
dt
2
Można pokazać, że wektor prędkości polowej jest proporcjonalny do prędkości
kątowej i ma jej kierunek:
1− →
1 −
1 −2 →
1 −
→
−
−
−
−
−
−
σ = →
r ×−
v = (→
r × (→
ω ×→
r )) = (→
r ·−
ω −→
r (→
r ·→
ω )) = r2 →
ω , (2.53)
2
2
2
2
−
−
ponieważ wektory →
r i→
ω są wzajemnie prostopadłe. Zatem mamy:
1 −
→
−
σ = r2 →
ω,
2
(2.54)
1
σ = r2 ϕ̇,
2
(2.55)
oraz
2.4
Opis ruchu w układzie współrzędnych biegunowych
Czasem wygodnie jest opisywać ruch płaski w układzie współrzędnych biegunowych.
Układ współrzędnych biegunowych to zdegenerowany do dwóch wymiarów układ
współrzędnych sferycznych. Układ taki szczególnie nadaje się do opisu ruchu krzywoliniowego z tzw. przyspieszeniem centralnym. Przyspieszenie centralne, jest to
przyspieszenie skierowane zawsze ku temu samemu punktowi O, który wygodnie
jest obrać za początek promieni wodzących.
Położenie punktu w układzie współrzędnych biegunowych opisują dwie współrzędne
r (odległość od początku układu współrzędnych) i kat biegunowy ϕ. Przy transformacji równań ruchu z układu współrzędnych kartezjańskich do układu współrzędnych biegunowych należy użyć następujących wzorów transformacyjnych.
q
y
r = x2 + y 2 , ϕ = arc tg .
x
(2.56)
2.4 Opis ruchu w układzie współrzędnych biegunowych
23
Dla transformacji odwrotnej mamy:
x = r cos ϕ, y = r sin ϕ.
(2.57)
Wzory transformacyjne dla składowych wektora przy obrocie układu
współrzędnych - przypadek dwuwymiarowy
Poszukujemy związków transformacyjnych dla składowych wektora wyznaczonych
w układach O i O’, układ O’ jest obrócony o pewien kąt ϕ względem układu O.
→
−
Weźmy pod uwagę dowolny wektor b w układzie współrzędnych kartezjańskich
O. Składowe tego wektora to:
bx = b cos ψ, by = b sin ψ.
(2.58)
W układzie współrzędnych O’ składowe tego wektora:
b0x = b cos(ψ − ϕ) = b(cos ψ cos ϕ + sin ψ sin ϕ) = bx cos ϕ + by sin ϕ
b0y = b sin(ψ − ϕ) = b(sin ψ sin ϕ + cos ψ sin ϕ) = −bx sin ϕ + by cos ϕ
(2.59)
Poszukiwany związek transformacyjny ma więc postać:
b0x = bx cos ϕ + by sin ϕ
b0y = −bx sin ϕ + by cos ϕ
(2.60)
Dla transformacji pomiędzy układami O’ i O mamy związki:
bx = b0x cos ϕ − b0y sin ϕ
by = b0x sin ϕ + b0y cos ϕ
(2.61)
24
Kinematyka
Otrzymujemy je mnożąc obie strony wyrażeń (2.60) kolejno przez sin ϕ i cos ϕ, a
następnie odejmując stronami pary otrzymanych wyrażeń.
Rozkład wektora prędkości na składową radialna i transwersalną
W układzie współrzędnych biegunowych w wielu przypadkach potrzebna jest zna−
−
jomość składowych wektorów →
v i→
a . Składowa w kierunku promienia wodzącego
→
−
→
−
→
−
r to składowa radialna ( v r lub a r ). Składowa styczna do okręgu o promieniu
−
r (prostopadła do wektora →
r ) o zwrocie wskazującym kierunek przyrostu kąta
−
−
biegunowego ϕ to składowa transwersalna (→
v ϕ lub →
a ϕ ).
Jeśli płaszczyzna x, y to płaszczyzna ruchu, to składowe radialna i transwersalna
→
−
dowolnego wektora b są następujące:
br = b cos(ψ − ϕ) = bx cos ϕ + by sin ϕ
bϕ = b sin(ψ − ϕ) = −bx sin ϕ + by cos ϕ
(2.62)
gdzie bx , by , to składowe wektora w układzie kartezjańskim x, y. W wyprowadzeniu
powyższych wzorów można posłużyć się schematem rozumowania przedstawionym
w poprzednim rozdziale (składowe br i bϕ to składowe wektora w układzie obróconym o kąt ϕ).
→
−
Ponieważ wzory (2.62) obowiązują dla dowolnego wektora b , to także dla wek−
tora prędkości →
v mamy:
vr = vx cos ϕ + vy sin ϕ
vϕ = −vx sin ϕ + vy cos ϕ,
(2.63)
Wzory transformacyjne pomiędzy współrzędnymi w układzie kartezjańskim i biegunowym są następujące:
x = r cos ϕ, y = r sin ϕ.
(2.64)
W czasie ruchu współrzędne r i ϕ są funkcjami czasu r=r(t), ϕ=ϕ(t). Składowe
wektora prędkości w układzie kartezjańskim:
vx = ẋ = ṙ cos ϕ − rϕ̇ sin ϕ
vy = ẏ = ṙ sin ϕ + rϕ̇ cos ϕ,
(2.65)
2.4 Opis ruchu w układzie współrzędnych biegunowych
25
Podstawiając otrzymane wyrażenia na vx i vy do wzoru (2.63) otrzymujemy poszukiwane wyrażenia na składowe wektora prędkości:
vr = ṙ, vϕ = rϕ̇.
(2.66)
Zauważymy ponadto, że ponieważ szybkość polowa
1
(2.67)
σ = r2ϕ̇
2
to składowa transwersalna prędkości ma następujący związek z szybkością polową:
2σ
.
(2.68)
vϕ =
r
Rozkład wektora przyspieszenia na składowe radialną i transwersalną
Dla składowych radialnej i transwersalnej wektora przyspieszenia mamy:
ar = ax cos ϕ + ay sin ϕ
aϕ = −ax sin ϕ + ay cos ϕ,
(2.69)
Składowe wektora przyspieszenia ax i ay otrzymamy różniczkując po czasie wyrażenia (2.65) na vx i vy :
ax = ẍ = r̈ cos ϕ − 2ṙϕ̇ sin ϕ − r(ϕ̈ sin ϕ + ϕ̇2 cos ϕ)
ay = ÿ = r̈ sin ϕ + 2ṙϕ̇ cos ϕ + r(ϕ̈ cos ϕ − ϕ̇2 sin ϕ).
(2.70)
Wstawiając otrzymane wyrażenia na ax i ay do wzorów (2.69) otrzymamy ostatecznie:
ar = r̈ − rϕ̇2
aϕ = 2ṙϕ̇ + rϕ̈.
(2.71)
Przykład - opis ruchu w układzie współrzędnych biegunowych
Kolista tarcza wiruje wokół swojej osi ze stałą prędkością kątową ω. Ze środka tarczy wyrusza biedronka. Porusza się ona wzdłuż wybranego promienia ze stałą prędkością v0. Znaleźć równania ruchu biedronki w układzie nieruchomym (widzialnym
przez zewnętrznego obserwatora), tor ruchu oraz składową radialną i transwersalną
wektora prędkości i przyspieszenia.
Z punktu widzenia zewnętrznego obserwatora najwygodniej jest opisywać ruch
biedronki w układzie współrzędnych biegunowych. Wtedy równania ruchu są
następujące:
r = v0 t,
ϕ = ωt.
(2.72)
26
Kinematyka
Torem ruchu jest spirala Archimedesa o równaniu
r=
v0
ϕ.
ω
(2.73)
Składowe wektora prędkości:
vr
= ṙ
= v0
vϕ = rϕ̇ = v0 ωt
(2.74)
Prędkość radialna jest stała i wynosi v0, a prędkość transwersalna rośnie liniowo
w czasie ruchu. Wartość prędkości zmienia się w czasie:
r
√
v = vr2 + vϕ2 = v0 1 + ω 2 t2 .
(2.75)
Składowe wektora przyspieszenia:
ar = −v0ω 2 t
aϕ = 2v0ω.
(2.76)
Długość tego wektora wynosi:
√
a = a2r + a2ϕ = v0ω 4 + ω 2 t2 .
r
2.5
(2.77)
Całkowanie równań ruchu
−
−
Jeśli znana jest zależność przyspieszenia od czasu →
a= →
a (t), to możemy znaleźć
prędkość, położenie, drogę i tor ruchu. Zagadnienie takie rozwiązuję się poprzez
całkowanie.
→
−
v (t) =
Z
→
−
a (t)dt + C
(2.78)
→
−
r (t) =
Z
→
−
v (t)dt + C 0
(2.79)
Podobnie
2.5 Całkowanie równań ruchu
27
Każde z powyższych równań wektorowych jest równoważne trzem równaniom
skalarnym, dla poszczególnych składowych. Stałe całkowanie C i C’ wyznacza się
z tzw. warunków brzegowych czyli związków podających prędkość i położenie w
−
−
−
−
jakiejś chwili czasu np. dla t=t0 mamy →
v (t0 )=→
v0 oraz →
r (t0)=→
r0 . Można również
posłużyć się całkami oznaczonymi - warunki brzegowe określają wówczas granice
całkowania. Mamy wówczas np.
−
Z →
Z t
v →
−
→
−
d
v
=
a (t)dt
(2.80)
→
−
v
t0
0
oraz
Z
→
−
Z t
r →
−
−
dr = →
v (t)dt
→
−
r
t0
0
(2.81)
zamiast równań (2.78) i (2.79).
−
Ruch jednostajny prostoliniowy (→
a =0)
→
−
−
Szczególnie prosto całkuje się przypadek ruchu, gdy →
a =0. Ponieważ ddtv = 0, to
−
prędkość jako wektor jest stała →
v (t)=const., a ruch odbywa się wzdłuż prostej.
Możemy przyjąć, że ruch odbywa się wzdłuż którejś z osi układu współrzędnych
np. osi x. Wektor prędkości ma wówczas tylko jedną składową:
→
−
b
v = v x,
dx
v=
,
dt
v = const.
(2.82)
dx = v dt
(2.83)
Równanie (2.83) można scałkować
Z x
x0
dx = v
Z t
t0
dt;
x − x0 = v(t − t0 ).
Mamy x(t) = x0 + v(t − t0 ) - położenie jest liniową funkcją czasu.
(2.84)
28
Kinematyka
Wykres zależności x = x(t) przedstawia rysunek powyżej. Na tym wykresie prędkość można odczytać z nachylenia prostej tg α = v.
Przebytą drogę możemy otrzymywać jako wynik całkowania zależności prędkości od czasu
s=v
Z t
t0
dt = v(t − t0 ).
(2.85)
Wartość tej całki jest równa polu powierzchni pod prostą przedstawiającą zależność prędkości od czasu. W tym przypadku jest to pole prostokąta o bokach v
i (t − t0 ).
−
Ruch ze stałym przyspieszeniem (→
a =const.)
Całkowanie równań ruchu jest również proste, kiedy przyspieszenie nie zależy od
−
czasu →
a (t) = const. W takim wypadku, jak łatwo pokazać, ruch odbywa się po
torze płaskim.
−
Z →
Z t
v →
→
−
−
−
−
→
−
d
v
=
a
dt,
v −→
v0 = →
a (t − t0 )
(2.86)
→
−
v
t0
0
oraz
−
d→
r
−
−
= →
v0 + →
a (t − t0 ).
dt
(2.87)
−
−
Po scałkowaniu tego ostatniego równania przyjmując →
r (t0)=→
r0 otrzymujemy:
1−
→
−
−
−
r =→
r0 + →
v0 (t − t0 ) + →
a (t − t0 ).
2
(2.88)
−
Równania (2.87) i (2.88) pokazują, że wektor prędkości →
v leży w płaszczyźnie
−
−
wyznaczonej przez wektory →
v0 i →
a . Na tej samej płaszczyźnie leży także wektor
→
−
→
−
przemieszczenia r − r 0 . W ogólności więc ruch ze stałym przyspieszeniem odbywa
−
się po torze płaskim, ale w przypadku, kiedy wektory prędkości początkowej →
v0 i
−
−
przyspieszenie →
a mają ten sam kierunek, albo kiedy →
v0 = 0, ruch odbywa się po
prostej, której kierunek wyznacza wektor przyspieszenia. Omówimy teraz oba te
przypadki dla przykładu ruchu w ziemskim polu grawitacyjnym.
2.5 Całkowanie równań ruchu
29
(a) Ruch prostoliniowy - spadek swobodny
−
−
W przypadku kiedy →
a =const. i prędkość początkowa →
v (0) = 0 ruch odbywa się
po prostej. Przyjmijmy, że ruch odbywa się wzdłuż osi z układu współrzędnych.
Ruch opisuje następujące kinematyczne ruchu ruchu
→
−
−
a = −g →
z.
(2.89)
ż(0) = 0, z(0) = h.
(2.90)
−
Przyspieszenie →
g jest skierowane przeciwnie do kierunku osi z. Równanie (2.89)
należy scałkować przy następujących warunkach początkowych:
W chwili początkowej t=0 ciało znajduje się na wysokości h i ma zerową prędkość
początkową.
Skalarne równanie ruchu ma postać
dvz
= g,
(2.91)
dt
wynika to z faktu, że prędkość ciała w spadku swobodnym rośnie (funkcja jest
rosnąca, jeśli pierwsza pochodna jest dodatnia). Mamy
Z v
z
0
dvz = g
Z t
0
dt,
vz = gt.
(2.92)
−
b
Prędkość jest więc funkcją liniową czasu →
v = −gtz.
Droga w tym ruchu:
1
1 Zt
(2.93)
vz dtz = g tdt = gt2 .
0
2 0
2
Na wykresie zależności prędkości od czasu droga jest polem powierzchni trójkąta
o podstawie t i wysokości gt:
s(t) =
Z t
Położenie ciała na osi z w funkcji czasu otrzymamy całkując wyrażenie:
dz
= −gt.
(2.94)
dt
Minus w wyrażeniu (2.94) gwarantuje, że położenie z(t) maleje w czasie ruchu.
Z z
h
dz = −g
Z t
0
tdt,
1
z = h − gt2 .
2
(2.95)
30
Kinematyka
Wykres zależności z(t) ma więc postać paraboli. Czas ruchu t s =
jdziemy wstawiając w równaniu (2.95) z = 0.
r
2h
g
zna-
(b) Ruch płaski - rzut ukośny
W ogólności, gdy kierunki przyspieszenia i prędkości początkowej nie pokrywają
się, ruch ze stałym przyspieszeniem odbywa się po torze płaskim. Ruch opisuje
następujące kinematyczne równanie ruchu:
→
−
−
a =→
g
(2.96)
−
Geometrię problemu obieramy tak, aby wektor →
g był skierowany przeciwnie do
→
−
−
kierunku osi z ( g =(0, 0, −g)), a wektor prędkości początkowej →
v0 leżał w płaszczyźnie
y,z i tworzył kąt α z osią y. Równanie wektorowe (2.96) odpowiada wtedy następującym trzem równaniom skalarnym:
ax = 0, ay = 0, az = −g.
(2.97)
Równania te należy scałkować przy następujących warunkach początkowych:
ẋ(0) = 0
x(0) = 0
ẏ(0) = v0 cos α
y(0) = 0
ż(0) = v0 sin α
z(0) = 0.
(2.98)
Przyjmujemy, że w chwili początkowej t=0, ciało znajduje się w początku układu
współrzędnych.
Po scałkowaniu równań (2.97) otrzymujemy wyrażenia przedstawiające zmiany
w czasie składowych wektora prędkości. Otrzymujemy:
vx (t) = 0,
vy (t) = v0 cos α,
vz (t) = v0 sin α − gt.
(2.99)
Widać więc, że ruch odbywa się w płaszczyźnie y,z, którą wyznaczył wektory
przyspieszenia i prędkości początkowej. Wzdłuż osi x ciało nie porusza się. Wzdłuż
osi y odbywa się ruch ze stałą prędkością, którą ciało nabyło w momencie wyrzucenia, a wzdłuż osi z ruch jest jednostajnie opóźniony.
2.6 Transformacja wektorów prędkości i przyspieszenia
pomiędzy układami odniesienia
31
Po scałkowaniu wyrażeń (2.99) otrzymujemy następujące równania ruchu:
1
(2.100)
x(t) = 0,
y(t) = v0t cos α,
z(t) = v0t sin α − gt2 .
2
Po wyrugowaniu czasu z równań ruchu otrzymujemy równanie toru:
g
z = y tg α − 2
y2.
(2.101)
2
2v0 cos α
Jest to równanie paraboli w płaszczyźnie y,z. Funkcja z(y) ma dwa miejsca zerowe
t.j. z = 0, gdy y = 0 oraz gdy:
v02
sin 2α.
(2.102)
g
Pierwsze rozwiązanie odpowiada położeniu ciała w chwili t = 0, drugie natomiast
wyznacza tzw. zasięg rzutu. Jak widać zasięg rzutu jest największy dla kąta α = π4 .
Wysokość maksymalną zmax ciało osiąga, gdy położenie na osi y wynosi połowę
zasięgu rzutu:
y=
1 v02
y=
sin 2α.
2g
(2.103)
Wtedy mamy
v02 sin2 α
zmax =
.
2g
Warto jeszcze zauważyć, że czas trwania ruchu:
τ=
v
u
u 2zmax
2t
g
(2.104)
(2.105)
Czas ten stanowi dwukrotność czasu trwania spadku swobodnego. Otrzymany
rezultat ilustruje tzw. zasadę niezależności ruchów. Zasada ta mówi, że jeśli ciało
porusza się ruchem złożonym, to każdy z tych składowych ruchów odbywa się bez zakłóceń w ten sposób jakby pozostałych ruchów nie było. Jak widać w rzucie ukośnym
ruch wzdłuż osi z to rzut w górę, a następnie spadek swobodny. Ruch ten odbywa
się niezależnie od ruchu jednostajnego wzdłuż osi y.
2.6
Transformacja wektorów prędkości i przyspieszenia
pomiędzy układami odniesienia
W kinematyce nie ma żadnych ograniczeń co do wyboru układu odniesienia względem, którego opisujemy ruch (chociaż najlepiej wybrać taki układ, w którym opis
matematyczny problemu jest najprostszy).
32
Kinematyka
Omówimy w tym rozdziale jedno z najważniejszych zagadnień kinematyki, a
mianowicie zagadnienie transformacji wielkości kinematycznych, gdy zmienia się
układ odniesienia względem, którego opisujemy ruch.
Podczas ruchu układu O’ względem układu O, układ O’ przyjmuje położenia,
które można przeprowadzić jedno w drugie przy pomocy transformacji, która jest
złożeniem przesunięcia równoległego (translacji) i obrotu (rotacji) wokół pewnej
osi. Innymi słowy, każda zmiana położenia układu O’ względem układu O jest
sumą translacji i rotacji układu O’ względem układu O.
−
−
Związki pomiędzy prędkością →
v 0 i przyspieszeniem →
a 0 mierzonymi przez obserwatora O’, a analogicznymi wielkościami i mierzonymi przez obserwatora O można
zapisać następująco:
→
−
−
v = →
v0+−
v→
D,
0
→
−
−
a = →
a +−
a→
D,
−
−
→ −→
v→
D = vtr + vrot ,
−
a→ = −
a→ + −
a→.
D
tr
rot
(2.106)
−
→
Wielkości −
v→
D i aD są odpowiednio dodatkową prędkością i przyspieszeniem, które
trzeba dodać, aby otrzymać prędkość i przyspieszenie względem układu O.
W rozważaniach tych korzystamy z zasady niezależności ruchów; osobno wyprowadz−
→
imy wyrażenia opisujące wkłady −
v→
D i aD związane z ruchem translacyjnym i rotacyjnym układu odniesienia.
Transformacja wektorów prędkości i przyspieszenia pomiędzy układami
O i O’, w przypadku ruchu translacyjnego układu O’
−
−
Pomiędzy wektorami położenia →
r i→
r 0 , zachodzi podczas ruchu translacyjnego
układu O’, prosty związek:
→
−
→
−
−
r (t) = →
r 0 (t) + R (t).
(2.107)
2.6 Transformacja wektorów prędkości i przyspieszenia
pomiędzy układami odniesienia
33
Różniczkowanie względem czasu daje:
0
→
−̇
→
−̇
−̇
r (t) = →
r (t) + R (t),
(2.108)
→
−
−
v =→
v0+−
v→
tr ,
(2.109)
czyli
gdzie:
→
−̇
−
v→
tr = R ,
→
−
b
v = ẋxb + ẏ yb + ż z,
→
−
v 0 = ẋ0 xb 0 + ẏ 0 yb0 + ż 0 zb0 .
(2.110)
Podobny związek możemy znaleźć dla przyspieszenia:
→
−
−
a =→
a0+−
a→
tr ,
(2.111)
gdzie:
→
−̈
−
a→
tr = R ,
→
−
b
a = ẍxb + ÿ yb + z̈ z,
→
−
a 0 = ẍ0 xb 0 + ÿ 0 yb0 + z̈ 0 zb0 .
(2.112)
Transformacja wektorów prędkości i przyspieszenia pomiędzy układami
O i O’ , w przypadku ruchu rotacyjnego układu O’
Rozważamy dwa kartezjańskie układy współrzędnych O i O’, z których jeden
−
obraca się ze stałą prędkością kątową →
ω dookoła osi z układu nieruchomego (oś
z’ pokrywa się z osią z układu nieruchomego). Poszukujemy związku jaki istnieje
pomiędzy wielkościami charakteryzującymi ruch ciała odniesiemy raz do układu
O, drugi raz do układu O’.
Pomiędzy składowymi wektora położenia x0 ,y 0 ,z 0 w układzie O’, a jego składowymi x,y,z w układzie O istnieją związki, który wyprowadziliśmy w poprzednim
rozdziale (patrz wzory (2.61)):
x = x0 cos ωt − y 0 sin ωt
y = x0 sin ωt + y 0 cos ωt
z = z0
(2.113)
34
Kinematyka
Różniczkując równania (2.113) względem czasu otrzymujemy wzory transformacyjne dla składowych wektora prędkości:
ẋ = ẋ0 cos ωt − ẏ 0 sin ωt − ω(x0 sin ωt + y 0 cos ωt)
ẏ = ẋ0 sin ωt + ẏ 0 cos ωt + ω(x0 cos ωt − y 0 sin ωt)
ż = ż 0 .
(2.114)
Następnie po kolejnym różniczkowaniu otrzymujemy wzory transformacyjne dla
składowych wektora przyspieszania:
ẍ = ẍ0 cos ωt − ÿ 0 sin ωt − 2ω(ẋ0 sin ωt + ẏ 0 cos ωt) − ω 2 (x0 cos ωt − y 0 sin ωt)
ÿ = ẍ0 sin ωt + ÿ 0 cos ωt + 2ω(ẋ0 cos ωt − ẏ 0 sin ωt) − ω 2 (x0 sin ωt + y 0 cos ωt)
z̈ = z̈ 0 .
(2.115)
Zastosowanie otrzymanych wzorów zilustrujemy na przykładzie.
Przykład - transformacja równań ruchu z układu znajdującego się w ruchu
obrotowym do układu w spoczynku
Wracamy do opisu ruchu biedronki na kulistej tarczy wirującej wokół swojej osi ze
stałą prędkością kątową ω. Biedronka wyrusza ze środka tarczy i porusza się wzdłuż
jednego z promieni ze stałą prędkością v0 . Znajdziemy równanie ruchu, składowe
wektorów prędkości i przyspieszenia oraz ich wartości z punktu wiedzenia obserwatora zewnętrznego (w układzie nieruchomym).
Równania ruchu w układzie wirującym :
x0 = v0t,
y 0 = 0,
z 0 = 0.
(2.116)
Przyjęliśmy więc, że biedronka porusza się wzdłuż osi x’ układu współrzędnych
związanego z obracającą się tarczą.
Po zastosowaniu wzorów transformacyjnych (2.113) dla składowych wektora
położenia, w układzie nieruchomym O mamy następujące równania ruchu:
x = v0t cos ωt,
y = v0t sin ωt,
z = 0.
(2.117)
Składowe wektora prędkości biedronki w układzie nieruchomym znajdujemy po
zróżniczkowaniu względem czasu równań ruchu (2.117). Mamy więc:
ẋ = v0 cos ωt − v0ωt sin ωt
ẏ = v0 sin ωt + v0ωt cos ωt
ż = 0.
(2.118)
2.6 Transformacja wektorów prędkości i przyspieszenia
pomiędzy układami odniesienia
35
Wartość prędkości:
√
v = v 0 1 + ω 2 t2
(2.119)
Składowe wektora przyspieszenia:
ẍ = −2v0ω sin ωt − v0ω 2 t cos ωt
ÿ = 2v0ω cos ωt − v0ω 2 t sin ωt
z̈ = 0.
(2.120)
Wartość przyspieszenia:
√
a = v 0 ω 4 + ω 2 t2
(2.121)
Wzór Coriolisa
Pokażemy teraz, że równania skalarne (2.114) i (2.115) odpowiadają następującym
wzorom transformacyjnym dla wektorów prędkości i przyspieszenia:
→
−
−
−
−
v =→
v0+→
ω ×→
r0
(2.122)
→
−
−
−
−
−
−
−
a =→
a 0 + 2→
ω ×→
v0+→
ω × (→
ω ×→
r 0)
(2.123)
Ten ostatni wzór (dla transformacji przyspieszenia) nosi nazwę wzoru Coriolisa.
Najpierw sprawdzimy, że równania skalarne (2.114) odpowiadają równaniu wektorowemu (2.122). Sprawdzimy to rzutując obie strony równości (2.122) na kierunki
osi liczbowych układu współrzędnych O:
→
−
−
−
−
v · xb = →
v 0 · xb + (→
ω ×→
r 0 ) · xb
→
−
−
−
−
v · yb = →
v 0 · yb + (→
ω ×→
r 0 ) · yb
→
−
−
−
−
v · zb = →
v 0 · zb + (→
ω ×→
r 0 ) · zb
(2.124)
W obliczeniach tych musimy użyć wzorów transformacyjnych dla wersorów osi
liczbowych:
xb = xb 0 cos ωt − yb0 sin ωt
yb = xb 0 sin ωt + yb0 cos ωt
zb = zb0
(2.125)
Wzory te wynikają ze wzorów transformacyjnych dla składowych dowolnego wektora (więc także dla wersorów osi liczbowych) przy obrocie układu współrzędb który w układzie O ma składowe x=(1,0,0),
b
nych (patrz wzory 2.61). Wersor x,
36
Kinematyka
b
w układzie O’ ma składowe x=(cos
ωt,− sin ωt,0). Podobnie wersor yb w układzie
O ma składowe (0,1,0), a w układzie O’ jego składowe to (sin ωt,cos ωt,0) . Dla
wersora zb w obu układach składowe są takie same: (0, 0, 1).
Po dokonaniu obliczeń z wyrażeń (2.124) otrzymujemy wzory transformacyjne
(2.114) dla składowych wektora prędkości. W obliczeniach tych należy pamiętać,
−
−
−
−
−
że składowe wektorów →
r 0, →
v 0, →
ω 0 są następujące: →
r 0 = (x0, y 0, z 0 ), →
v 0 = (ẋ0, ẏ 0 , ż 0 )
−
oraz →
ω 0 = (0, 0, ω).
W podobny sposób można sprawdzić, że równania skalarne (2.115) odpowiadają
równaniu wektorowemu (2.123). Aby to sprawdzić rzutujemy obie strony wzoru
Coriolisa na osie x,y,z:
→
−
−
−
−
−
−
−
a · xb = →
a 0 · xb + 2(→
ω ×→
v 0 ) · xb + (→
ω × (→
ω ×→
r 0 )) · xb
→
−
−
−
−
−
−
−
a · yb = →
a 0 · yb + 2(→
ω ×→
v 0 ) · yb + (→
ω × (→
ω ×→
r 0)) · yb
→
−
−
−
−
−
−
−
a · zb = →
a 0 · zb + 2(→
ω ×→
v 0) · zb + (→
ω × (→
ω ×→
r 0 )) · zb
(2.126)
Po wykonaniu obliczeń ze wzorów (2.126) otrzymujemy wzory transformacyjne
(2.115).
Wzór Coriolisa (2.123) można zapisać następująco:
→
−
−
−
a =→
a0+→
ad ,
(2.127)
gdzie
→
−
−
−
−
−
−
ad = 2→
ω ×→
v0+→
ω × (→
ω ×→
r 0 ),
(2.128)
jest dodatkowym przyspieszeniem, wynikającym z ruchu obrotowego układu O’,
jakie trzeba dodać, aby otrzymać przyspieszenie ciała względem układu nieru−
−
−
chomego. W wyrażeniu na →
ad mamy dwa wkłady. Pierwszy 2(→
ω ×→
v 0 ) to przyspiesze−
−
−
nie Coriolisa, drugi →
ω × (→
ω ×→
r 0 ), to przyspieszenie dośrodkowe. Zauważmy,
że przyspieszenie Coriolisa pojawia się tylko wtedy, gdy mamy do czynienia z
ruchem ciała w układzie obracającym się. Przyspieszenie, to znika jednak, gdy
−
−
ciało porusza się wzdłuż osi obrotu (wtedy kierunki →
v0i→
ω są równoległe). Drugi
−
wyraz w wyrażeniu na →
ad to przyspieszenie dośrodkowe. Jest to wektor prostopadły
do osi obrotu i zawsze w czasie ruchu ku niej skierowany. Aby to wykazać, rozłóżmy
−
−
wektor położenia →
r 0 na część prostopadłą i równoległą do kierunku wektora →
ω:
→
−
−
r0=−
r→ + →
r .
(2.129)
⊥
k
−
→
− →
−
Wtedy, biorąc pod uwagę, że →
ω ·−
r→
⊥ = 0 oraz ω × rk = 0 mamy:
0
2−
→
−
−
−
−
−
→0
ω × (→
ω ×→
r 0) = →
ω × (→
ω ×−
r→
⊥ ) = −ω r⊥ .
(2.130)
2.6 Transformacja wektorów prędkości i przyspieszenia
pomiędzy układami odniesienia
37
Dyskusja wzorów transformacyjnych
Podczas ruchu układu O’ względem układu O układ O’ przyjmuje położenia, które
można przeprowadzić jedno w drugie przy pomocy transformacji nie zmieniającej wzajemnej odległości punków - tzw. transformacji izometrycznej. Każda taka
transformacja, jak wiadomo z geometrii analitycznej, jest złożeniem przesunięcia
równoległego i obrotu wokół pewnej osi.
−
−
Pokazaliśmy, że związki pomiędzy prędkością →
v i przyspieszeniem →
a mier0
0
−
−
zonymi przez obserwatora O, a analogicznymi wielkościami →
v i→
a mierzonymi
przez obserwatora O’ można zapisać następująco:
→
−
−
→
− →
−0
v = →
v0+−
v→
tr + ω × r
→
−
−
→
− →
−0
→
−
→
− →
−0
a = →
a0+−
a→
tr + 2( ω × v ) + ω × ( ω × r ).
(2.131)
Należy tu wspomnieć, że te wzory transformacyjne wyprowadzono, biorąc pod
uwagę dwa uproszczenia. Przyjęliśmy mianowicie, że układ obracający się porusza
−
się ze stałą prędkością kątową (→
ω = const.) oraz, że w czasie obrotu kierunek osi z 0
pokrywa się z kierunkiem osi z (przyjęliśmy dwuwymiarową transformację obrotu).
To drugie uproszczenie nie miało jednak wpływu na jakościowy obraz otrzymanych
−
wzorów transformacyjnych. Natomiast, gdyby przyjąć w rozważaniach, że →
ω =
0
→
−
→
−̇
→
−
ω (t) to we wzorze Coriolisa pojawiłby się dodatkowy wyraz ω × r . Ostatecznie
więc wzór Coriolisa ma postać:
→
−
−
→
− →
−0
→
−
→
− →
−0
→
−̇ →
−0
a = →
a0+−
a→
tr + 2( ω × v ) + ω × ( ω × r ) + ω × r .
(2.132)
Zauważmy, że ciało spoczywające w układzie O’ ma w układzie O prędkość i
przyspieszenie różne od zera:
→
−
−
→
− →
−0
vu = →
v0+−
v→
tr + ω × r
→
−̇ →
−0
→
−
−
→
−
→
− →
−0
au = →
a0+−
a→
tr + ω × ( ω × v ) + ω × r .
(2.133)
Są to tzw. prędkość i przyspieszenie unoszenia. Wynikają one z ruchu układu O’.
38
Kinematyka
Rozdział 3
Dynamika punktu materialnego
Prawa ruchu Newtona wprowadziły do fizyki pojęcia siły i masy. Te pojęcia wprowadzono dla opisu ruchu abstrakcyjnego ciała - punktu materialnego. Punkt materialny to bezwymiarowy obiekt obdarzony masą. Pojęcie to jest idealizacją rzeczywistego ciała materialnego pozwalającą na prosty opis matematyczny jego ruchu.
Model ten stosować można wtedy, gdy rozmiary ciała nie odgrywają roli w przebiegu zjawiska fizycznego.
3.1
Zasada bezwładności i transformacja Galileusza
Pierwsze prawo ruchu zwane też zasadą bezwładności odpowiada na pytanie jak
zachowuje się cząstka nie podlegająca żadnemu oddziaływaniu ze strony otoczenia.
Zauważmy, że chodzi tutaj o pewną idealizację. Cząstka, która nie podlega żadnemu oddziaływaniu zewnętrznemu - cząstka odosobniona, w praktyce nie istnieje.
Cząstka taka musiałaby być jedyną cząstką Wszechświata, poza tym, cząstka taka
byłaby nieobserwowalna (w procesie obserwacji zachodzi zawsze oddziaływanie
pomiędzy cząstką, a przyrządem obserwacyjnym). Zasadę bezwładności traktujemy jako postulat uogólniający wyniki doświadczeń przeprowadzonych z ciałami,
które ściśle biorąc nie są odosobnione.
Pierwsza zasada dynamiki brzmi następująco:
Cząstka odosobniona zawsze pozostaje w spoczynku lub porusza się po linii prostej
ze stałą prędkością.
Zauważmy jednak, że ruch zawsze opisujemy względem jakiegoś układu odniesienia. Tak wybrany układ odniesienia, względem którego cząstka nie podlegająca
oddziaływaniu, cząstka odosobniona spoczywa lub jest w ruchu jednostajnym po
linii prostej, nazywamy układem inercjalnym.
Zasadę bezwładności uznać więc możemy za postulat istnienia układu inercjal-
40
Dynamika punktu materialnego
nego. Można ponadto znaleźć kryterium, które wyróżni układy inercjalne spośród
wszystkich innych układów odniesienia. Można otóż pokazać, że każdy układ
O’ poruszający się względem układu inercjalnego O ruchem postępowym bez
przyspieszenia jest też układem inercjalnym. Wynika to ze wzoru Coriolisa:
→
−
−
−
−
−
−
−
−
−
−
a =→
a0+→
a tr + 2→
ω ×→
v0+→
ω × (→
ω ×→
r 0) + →
ω ×→
r 0.
(3.1)
−
−
Biorąc pod uwagę, że dla ruchu układu O’ mamy →
a tr = 0 oraz →
ω = 0 (co zachodzi
dla ruchu postępowego przez przyspieszenie) ze wzoru Coriolisa wynika:
→
−
−
a =→
a0
(3.2)
Zatem w przypadku, gdy oddziaływanie zewnętrzne nie występuje w układzie O
−
−
(tzn. gdy →
a = 0) mamy także →
a ’= 0, tzn. brak jest także oddziaływań zewnętrznych
w układzie O’. Układ O’ jest więc układem inercjalnym.
Zasada bezwładności stwarza podstawy podziału wszystkich możliwych układów
odniesienia na inercjalne i takie, w których zasada bezwładności nie obowiązuje.
Formułując prawa dynamiki będziemy zakładać, że układ w którym rozważamy
ruch jest inercjalny. Odróżnia to rozważania w dynamice punktu materialnego od
rozważań w kinematyce, gdzie było rzeczą obojętną, w którym układzie opisywaliśmy ruch.
Transformacja Galileusza
Położenie dowolnego punktu P w układach inercjalnych O i O’ dane jest przez
−
−
wektory położenia →
r i→
r ’ powiązane ze sobą tzw. transformacją Galileusza.
−
−
Pomiędzy wektorami →
r i→
r ’ istnieje związek:
→
− −0
→
−
r = R +→
r .
(3.3)
→
−
Gdy układy O i O’ są układami inercjalnymi wówczas zmiana wektora R można
być spowodowana tylko ruchem translacyjnym ze stałą prędkością:
→
−
→
−
−
r0=→
r − V t;
→
−
V = const.
(3.4)
3.2 II zasada dynamiki Newtona
41
W sytuacji, gdy prędkość względna ma kierunek osi x oraz przyjmując, że w chwili
t=0 początki obu układów pokrywały się, to równanie wektorowe (3.4) odpowiada
trzem skalarnym równaniom transformacyjnym:
x0 = x − V t
y0 = y
z0 = z
(3.5)
Trzeba tu jeszcze dodać t’=t. Te wzory transformacyjne dla współrzędnych pomiędzy układami inercjalnymi to tzw. transformacja Galileusza.
Trzeba tu zauważyć, że żądanie niezmienniczości praw fizyki ze względu na
transformację Galileusza nakłada określone ograniczenia na możliwą postać praw
fizyki. Zauważmy, że z transformacji Galileusza wynika, że odległości przestrzenne,
zmiany prędkości, przyspieszenia i długości mierzonych przedziałów czasowych są
takie same dla obserwatorów w układach O i O’.
3.2
II zasada dynamiki Newtona
Z zasady bezwładności wiemy, że w inercjalnym układzie odniesienia cząstka nie
podlegająca żadnemu oddziaływaniu spoczywa lub porusza się ruchem jednostajnym po prostej. Zatem jeśli obserwator w tym układzie zauważy, że ruch cząstki
nie jest ruchem jednostajnym po prostej, to powie, że cząstka podlega oddziaływaniu. Za miarę tego oddziaływania można uznać przyspieszenie cząstki, ta bowiem
wielkość fizyczna opisuje zmiany prędkości, a więc wspomniane zmiany odstępstwa
od ruchu ze stałą prędkością po linii prostej.
→
−
Miarą oddziaływania jest siła F . Zmiany prędkości i przyspieszenie mają kierunek działającej siły. Drugie prawo ruchu ma postać:
→
−
F
→
−
a =
(3.6)
m
Przyspieszenie jest proporcjonalne do przyłożonej siły i ma kierunek prostej, wzdłuż
której siła jest przyłożona.
Masa, która pojawia się w tym równaniu ruchu charakteryzuje właściwość
cząstki - stawianie oporu przy jej przyspieszaniu (podatność na działanie siły).
Cząstka o dużej masie ma większą bezwładność, stawia większy opór przy przyspieszaniu na skutek działania siły, niż cząstka o małej masie.
Wydaje się, że zasadę bezwładności (I zasadę dynamiki) można by uznać za
szczególny przypadek II prawa ruchu. Z równania (3.6) wynika mianowicie, że gdy
42
Dynamika punktu materialnego
→
−
−
−
na ciało nie działa żadna siła ( F = 0), mamy →
a = 0, a zatem →
v = const., co oznacza, że cząstka porusza się ruchem jednostajnym po linii prostej. Rozumowanie
takie nie jest jednak poprawne. Należy pamiętać, że najważniejszą rolę jaką pełni I
prawo ruchu w dynamice jest wyróżnienie spośród wszystkich układów odniesienia
układów inercjalnych. Oczywiste jest zatem, że w układzie inercjalnym, w którym
obowiązuje II prawo ruchu spełniona jest zasada bezwładności.
→
−
Doświadczenie uczy nas, że w ogólności siła F jest funkcją położenia, prędkości
i czasu:
→
−
→
− − →
F = F (→
r ,−
v , t)
(3.7)
Ustalenie zależności (3.7), wyrażanych później w postaci praw empirycznych stanowi
jeden z ważniejszych problemów fizyki doświadczalnej.
Drugie prawo ruchu w postaci wektorowej ma postać:
−̈
−
−̇
m→
r (t) = F (→
r ,→
r , t)
(3.8)
Równanie to jest równoważne układowi dwóch równań skalarnych. Z matematycznego punktu widzenia są to równania różniczkowe drugiego rzędu, a ich
rozwiązaniem jest funkcja wektorowa:
→
−
r (t) = x(t)xb + y(t)yb + z(t)zb
(3.9)
→
−
wyznaczająca położenie cząstki w każdej chwili czasu. Zatem znajomość siły F
−
działającej na cząstkę i warunków początkowych tzn. położenia początkowego →
r0
→
−
i prędkości początkowej v 0 pozwalają z równania (3.8) jednoznacznie wyznaczyć
−
funkcję →
r (t) tzn. wyznaczyć położenie cząstki w dowolnej chwili czasu.
3.3
Całkowanie drugiego prawa ruchu
Drugie prawo ruchu
−̇
−̈
−
r , t),
r (t) = F (→
r ,→
m→
(3.10)
jest równaniem różniczkowym drugiego rzędu. Przedstawimy trzy przykładów
→
−
całkowania tego równania, gdy: F = const. (ruch w stałym jednorodnym polu
→
− →
− −
→
− →
− −
elektrycznym), F = F (→
r )(ruch drgający) oraz F = F (→
v )(ruch w stałym jednorodnym polu magnetycznym).
Ruch w stałym jednorodnym polu elektrycznym
3.3 Całkowanie drugiego prawa ruchu
43
Na cząstkę o ładunku q w stałym jednorodnym polu elektrycznym działa siła
→
−
→
−
F = qE,
(3.11)
→
−
gdzie E jest natężeniem pola elektrycznego. Wektor natężenia pola elektrycznego
→
−
w stałym jednorodnym polu nie zmienia swojej wartości ani kierunku ( E = const).
Przedstawimy rozwiązanie równania Newtona
→
−
−̈
m→
r (t) = q E
(3.12)
w przypadku, gdy w chwili początkowej cząstka znajdowała się wpoczątku układu
→
−
−
−
współrzędnych (→
r (0)= 0) i miała prędkość →
v 0= 0. Przyjmijmy, że wektor E
→
−
skierowany jest wzdłuż osi z układu współrzędnych - E =(0, 0, E) oraz, że wektor
→
−
v 0 leży w płaszczyźnie y,z i jest nachylony pod kątem θ do kierunku osi z.
Równanie (3.12) odpowiada układowi trzech równań skalarnych:
ẍ = 0,
ÿ = 0,
z̈ =
q
E,
m
(3.13)
które należy scałkować przy następujących warunkach początkujących:
x(0) = 0
ẋ(0) = 0
y(0) = 0
ẏ(0) = v0 sin θ
z(0) = 0
ż(0) = v0 cos θ
(3.14)
Po scałkowaniu równań (3.13) otrzymujemy wyrażenia przedstawiające zmiany w
czasie składowych wektora prędkości. Otrzymujemy:
vx (t) = 0,
vy (t) = v0 sin θ,
vz (t) = v0 cos θ +
qE
t.
m
(3.15)
Widać więc, że wzdłuż osi x ciało nie porusza się. Ruch jest płaski w płaszczyźnie,
→
−
−
którą wyznaczyły wektory pola E i prędkości początkowej →
v 0. Wzdłuż osi y ruch
odbywa się ze stałą prędkością, która jest składową wektora prędkości początkowej.
Te wyniki stają się oczywiste jeśli zauważyć, że wzdłuż osi x i y nie działa żadna
siła - ciało porusza się więc bez przyspieszenia. Natomiast wzdłuż osi z ruch jest
jednostajnie przyspieszony (z przyspieszeniem qE
) - w tym kierunku działa wektor
m
stałej siły.
Po scałkowaniu równań (3.15) otrzymujemy następujące równania ruchu:
x(t) = 0,
y(t) = vo t sin θ,
z(t) = vo t cos θ +
qE 2
t.
2m
(3.16)
Zauważmy, że gdy θ= 0 (kierunek prędkości początkowej cząstki pokrywa się z
→
−
kierunkiem pola E ) cząstka porusza się tylko wzdłuż osi z.
44
Dynamika punktu materialnego
W ogólności jednak torem ruchu jest parabola o równaniu:
z(t) = y ctg θ + y 2
qE
(1 + ctg2 θ).
2
2mvo
(3.17)
Parabola ma dwa miejsca zerowe:
y1 = 0,
ale dla θ=
π
2
2mv02 ctg θ
y2 = −
,
qE 1 + ctg2 θ
(3.18)
przecina oś y tylko w jednym punkcie y= 0.
Ruch pod wpływem siły sprężystej
Drgania (ruch pod wpływem siły sprężystej) są bardzo powszechne w przyrodzie.
Siłą sprężystą (elastyczną) opisuje wyrażanie:
→
−
−
F = −k →
r.
(3.19)
Jest to siła zwrotna (przyciągająca) stale skierowana do jednego punktu w przestrzeni,
który nazywamy centrum siły sprężystej. Punkt materialny przyciągany jest z siłą
proporcjonalną do odległości od centrum działania siły. Siłę elastyczną w przybliżeniu można realizować za pomocą sprężyny. Punkt materialny poruszający się
pod wpływem siły elastycznej nazywamy oscylatorem harmonicznym. Jego ruch
nosi nazwę drgań harmonicznych.
Równanie Newtona w przypadku siły sprężystej ma postać:
−̈
−
m→
r = −k →
r.
(3.20)
Równanie to można zapisać w postaci:
→
−̈
−
r + ω02 →
r = 0,
(3.21)
r
gdzie
= mk . Po rozpisaniu na składowe w układzie kartezjańskim otrzymujemy
układ trzech równań różniczkowych:
ω02
ẍ + ω02x = 0, ÿ + ω02y = 0, z̈ + ω02 z = 0.
(3.22)
Rozwiązaniem tych równań jest układ trzech funkcji:
x = Ax cos ω0 t + Bx sin ω0 t
y = Ay cos ω0 t + By sin ω0 t
z = Az cos ω0 t + Bz sin ω0 t
(3.23)
3.3 Całkowanie drugiego prawa ruchu
45
Są to tzw. całki ogólne równań różniczkowych. Współczynniki A i B występują
w tych równaniach w ogólności mogą być liczbami zespolonymi. Należy tu zauważyć, że całek ogólnych można by także poszukiwać w postaci innych funkcji
czasu: C1e(iω0 t) + C2 e(−iω0t) lub C cos(ω0t + ϕ), gdzie zapewniamy sobie, że C jest
liczbą rzeczywistą. Jednak po narzuceniu na rozwiązania warunków początkowych
otrzymujemy już tzw. całki szczególne, które niezależnie od formy całek ogólnych
przyjmują już tylko jedną taką samą postać opisującą dany problem fizyczny.
Przyjmując następujące warunki początkowe:
→
−
−
−
−
r (0) = →
r , →
v (0) = →
v ,
(3.24)
0
0
→
−
→
−
możemy wyznaczyć stałe A =(Ax , Ay , Az ) oraz B =(Bx , By , Bz ) w równaniach
(3.23). Otrzymujemy ostatecznie:
→
−
v0
→
−
→
−
r (t) = r0 cos ω0 t +
sin ω0 t
(3.25)
ω0
Ruch harmoniczny jest więc ruchem płaskim w płaszczyźnie wyznaczonej przez
−
−
wektory →
r0 i →
v0 . Stała ω0 to częstość drgań własnych. Można pokazać, że w ogólności torem ruchu jest elipsa. Zauważymy jeszcze, że ruch opisany równaniem
, mamy:
(3.25) jest periodyczny. Po krótkich obliczeniach, jeśli przyjąć T = 2π
ω0
→
−
−
r (t + T ) = →
r (t).
(3.26)
Czas T jest okresem ruchu harmonicznego.
Ruch w stałym jednorodnym polu magnetycznym
Na ciało o ładunku q działa w polu magnetycznym siła Lorentza:
→
−
→
−
−
F = q(→
v × B)
(3.27)
Zauważmy, że siła ta działa jedynie na ładunek będący w ruchu, chociaż znika
→
− →
−
wtedy, gdy ruch odbywa się wzdłuż kierunku pola magnetycznego B ( B jest wektorem indukcji magnetycznej). Działająca siła jest zawsze prostopadła do wektora
prędkości nie może więc spowodować zmiany wartości wektora prędkości (jest to
tzw. siła żyroskopowa).
Przedstawimy rozwiązanie równania Newtona:
→
−
−̈
−
m→
r = q(→
v × B ),
(3.28)
dla następujących warunków początkowych. Przyjmujemy, że w chwili początkowej
−
cząstka znajdowała się w początku układów współrzędnych →
r (0)= 0, oraz posi−
adała prędkość początkową →
v (0)= v0. Przyjmujemy następującą geometrię problemu: pole magnetyczne skierowane jest wzdłuż osi z układów współrzędnych
46
Dynamika punktu materialnego
→
−
B =(0,0,B), a wektor prędkości początkowej znajduje się w płaszczyźnie x,z i
→
−
nachylony jest pod kątem θ do kierunku pola B . Przy tak zadanej geometrii
problemu równanie wektorowe (3.28) odpowiada następującym trzem równaniom
skalarnym:
ẍ = ω ẏ, ÿ = −ω ẋ,
z̈ = 0
(3.29)
gdzie przyjęliśmy oznaczenie ω = qB
.
m
Warunki początkowe, to układ trzech równań skalarnych dla wektora prędkości
początkowej:
ẋ(0) = v0 sin θ, ẏ(0) = 0, ż(0) = v0 cos θ
(3.30)
oraz trzech równań skalarnych opisujących położenie początkowe cząstki:
x(0) = 0, y(0) = 0, z(0) = 0
(3.31)
Rozwiązanie równania z̈ = 0 opisującego ruch wzdłuż osi z jest łatwe. Najpierw
po scałkowaniu otrzymujemy równanie opisujące prędkość wzdłuż osi z:
vz (t) = v0 cos θ
(3.32)
z(t) = v0t cos θ.
(3.33)
a następnie równanie ruchu
Widać więc, że ruch wzdłuż osi z jest ruchem jednostajnym prostoliniowym (siła
Lorentza nie działa wzdłuż osi z).
Natomiast scałkowanie równań opisujących ruch wzdłuż osi x i y nie jest możliwe
- w równaniach tych nie można rozdzielić zmiennych. Aby rozwiązać układ dwóch
pozostałych równań różniczkowych najpierw należy obniżyć ich rząd wprowadzając wyrażenia na prędkości wzdłuż osi: vx = ẋ i vy = ẏ . Mamy wtedy:
v̇x = ωvy , v̇y = −ωvx .
(3.34)
Następnie obie strony równań różniczkujemy po czasie. Mamy wtedy:
v̈x = ω v̇y , v̈y = −ω v̇x .
(3.35)
Kombinując ze sobą oba układy równań (3.34) i (3.35) mamy:
v̈x = −ω 2 vy , v̈y = −ω 2 vx .
(3.36)
Te równania mają już rozdzielone zmienne i można je scałkować przy następujących warunkach początkowych:
v̇x (0) = 0, v̇y (0) = −ωv0 sin θ,
(3.37)
3.3 Całkowanie drugiego prawa ruchu
47
które wynikają z równań (3.34) i (3.30). Równania (3.37) są równaniami typu oscylatora harmonicznego dla zmiennych vx i vy . Rozwiązania tych równań różniczkowych
to funkcje o postaci A sin ωt + B cos ωt, gdzie stałe A i B wyznaczają warunki
początkowe. Po narzuceniu warunków początkowych na rozwiązania otrzymujemy:
vx = v0 sin θ cos ωt
vy = −v0 sin θ sin ωt.
(3.38)
Po dalszym całkowaniu, dla warunków początkowych danych równaniami (3.31),
ostatecznie otrzymujemy:
x(t) = a sin ωt,
y(t) = a(cos ωt − 1),
(3.39)
gdzie a = vω0 sin θ.
Torem ruchu cząstki w płaszczyźnie x,y jest okrąg opisany równaniem x 2 +
(y − a)2 = a2 o promieniu a = vωo sin θ i środku w punkcie o współrzędnych (x=0,
q
y=−a). Ruch po okręgu jest ruchem jednostajnym z prędkością v = vx2 + vy2 =
v0 sin θ. Prędkość kątowa w tym ruchu wynosi ω = av = qB
, co wskazuje na celowość
m
wcześniej przyjętego oznaczenia (ω nazywa się częstością cyklotronową).
Podsumowując, równania ruchu cząstki są następujące:
x(t) = a sin ωt
y(t) = a(cos ωt − 1)
z(t) = v0t cos θ.
(3.40)
Cząstka naładowana porusza się w polu magnetycznym po linii śrubowej. Osią
tej linii śrubowej jest prosta x = 0, y = −a. Wzdłuż osi z jest to ruch jednostajny
prostoliniowy, a w płaszczyźnie x, y cząstka porusza się po okręgu.
Jednak w przypadku, gdy θ = 0 (wektor prędkości początkowej cząstki jest
→
−
zgodny z kierunkiem pola B ) promień okręgu a = 0. W tym przypadku cząstka
porusza się ruchem jednostajnym prostoliniowym po prostej - równania ruchu są
następujące:
x(t) = 0,
y(t) = 0,
z(t) = vo t.
(3.41)
48
Dynamika punktu materialnego
W przypadku, gdy θ = ± π2 (wektor prędkości początkowej cząstki jest prostopadły
→
−
do kierunku pola B ) cząstka porusza się ruchem jednostajnym po okręgu o promieniu a = amax = vω0 . Ruch cząstki opisują następujące równania ruchu:
x(t) = a sin ωt,
3.4
y(t) = a(cos ωt − 1),
z(t) = 0.
(3.42)
Uogólniona postać II zasady dynamiki i zasada zachowania pędu
Pędem cząstki nazywa się iloczyn jej masy i prędkości:
→
−
−
p = m→
v.
(3.43)
Pęd jest wielkością wektorową - ma kierunek wektora prędkości. Żeby zmienić
pęd cząstki potrzebna jest siła. Drugie prawo ruchu zostało sformułowane przez
Newtona następująco:
−
d→
p
→
−
F =
(3.44)
dt
−
Chociaż w swoich dziełach iloczyn m→
v Newton nazywał ”ilością ruchu”(quantity
of motion). Drugie prawo ruchu w tej wersji mówi, że szybkość zmian pędu cząstki
jest proporcjonalna do działającej siły. To sformułowanie jest ogólniejsze od poprzedniego wyrażonego w formie:
→
−
−
F = m→
a,
(3.45)
ponieważ dotyczy także przypadku ruchu ciał ze zmieniającą się masą. Dokonując
różniczkowania po prawej stronie wyrażenia (3.44) otrzymujemy mianowicie:
−
d→
v
dm
d→
−
−
p =m
+→
v
.
(3.46)
dt
dt
dt
→
−
−
Jeżeli w czasie ruchu masa jest stała, to dm = 0 i mamy F = m→
a . Równanie (3.45)
dt
możemy stosować więc do opisu ruchu ciał o stałej masie. W przypadku jednak,
3.4 Uogólniona postać II zasady dynamiki i zasada zachowania pędu
49
kiedy masa poruszającego ciała zmienia się, jak to ma miejsce np. w przypadku
rakiety, która spala paliwo w czasie lotu albo w przypadku ruchu wagonu, z którego
wysypuję się węgiel itp. musimy stosować bardziej ogólne prawo ruchu w postaci
wyrażenia (3.44). Należy tu także stwierdzić, że tylko uogólniona postać II zasady
dynamiki obowiązuje w fizyce relatywistycznej. Według dynamiki relatywistycznej
masa jest funkcją prędkości m=m(v).
Wyrażenie (3.44) nazywane jest różniczkową formą II zasady dynamiki. Drugie
prawo ruchu można jednak także wyrazić w postaci całkowej. Z równania (3.44)
mamy
→
−
−
d→
p = F dt,
(3.47)
a stąd
→
−
−
p (t) − →
p (t0 ) =
Z t
→
−
t0
F (t)dt.
(3.48)
Wartość całki po prawej stronie wyrażenia (3.48) nazywa się popędem lub impulsem siły:
Z t
→
−
→
−
F (t)dt.
I =
t0
(3.49)
Na wykresie przedstawiającym zależność siły od czasu wartość popędu (impulsu)
siły, to pole powierzchni pod krzywą.
Całkowa postać II zasady dynamiki ma szczególne zastosowanie w przypadku,
gdy działająca siła jest szybkozmienną funkcją czasu. Jest to tzw. siła impulsowa. Typowy wykres zależności F = F(t) dla siły impulsowej przedstawia rysunek
powyżej - siła impulsowa ma dużą wartość w krótkim przedziale czasu i poza tym
przedziałem czasu przyjmuje wartość zerową.
Wychodząc z równania Newtona
−
d→
p
→
−
= F,
dt
(3.50)
50
Dynamika punktu materialnego
→
−
w przypadku, gdy nie ma sił ( F =0) otrzymujemy:
−−−→
→
−
p = const.
(3.51)
Tak więc w takim przypadku podczas ruchu pęd jest stałym wektorem. Twierdzenie wyrażone przez (3.51) stanowi zasadę zachowania pędu dla punktu materialnego:
W układzie izolowanym, gdy nie działają siły zewnętrzne pęd cząstki nie zmienia
się.
Poprzez zasadę zachowania wielkości fizycznej rozumiemy prawo przyrody stwierdzające, że w dowolnych chwilach czasu dana wielkość ma tą samą wartość. Zasady
zachowania pozwalają na przewidywanie przebiegu procesów fizycznych - muszą
one przebiegać tak, by nie zmieniały się wartości zachowywanych wielkości fizycznych.
3.5
II zasada dynamiki dla ruchu obrotowego i zasada zachowania momentu pędu
Mnożąc obie strony równania Newtona
−
d→
p
→
−
= F,
dt
(3.52)
−
d→
p
→
−
→
−
−
r ×
=→
r × F.
dt
(3.53)
−
wektorowo przez →
r otrzymujemy:
Lewą stronę tego równania można dalej przekształcać. Skorzystajmy ze związku
−
−
d →
d→
p
d→
r
−
−
−
(−
r ×→
p)=→
r ×
+
×→
p.
dt
dt
dt
(3.54)
Zauważmy, że iloczyn wektorowy:
−
d→
r
−
−
−
×→
p =→
v × m→
v = 0.
dt
(3.55)
Zatem wyrażenie (3.53) można zapisać następująco:
d →
→
−
−
−
(−
r ×→
p)=→
r × F.
dt
(3.56)
3.5 II zasada dynamiki dla ruchu obrotowego i zasada zachowania momentu pędu
51
→
−
−
→
−
Iloczyn wektorowy →
r × F nazywamy momentem siły i oznaczamy przez M :
−
→ − →
−
M =→
r × F.
(3.57)
−
→
Wartość tego wektora |M | = rF sin θ można wyrazić jako iloczyn wartości siły F
i jej ramienia r⊥ (r⊥ = r sin θ)
M = r⊥ F.
(3.58)
−
−
Iloczyn wektorowy →
r ×→
p nazywamy momentem pędu i oznaczamy przez L:
→
−
−
−
L =→
r ×→
p.
(3.59)
→
−
−
−
Wektor L jest z definicji prostopadły do płaszczyzny, w której leżą wektory →
r i→
p.
Moment pędu zmienia na ogół wartość i kierunek podczas ruchu cząstki. Jednakże,
gdy ruch ten zachodzi stale w jednej płaszczyźnie (jest ruchem płaskim) to wektor
L ma stały kierunek prostopadły do płaszczyzny ruchu. Także odwrotnie, jeśli L
ma stały kierunek podczas ruchu cząstki, to ruch ten musi być ruchem płaskim.
Z równania Newtona otrzymaliśmy związek:
→
−
dL
−
→
= M.
(3.60)
dt
Równanie to wyraża II zasadę dynamiki dla ruchu obrotowego.
−
→
Gdy M = 0, wtedy z równania (3.60) wynika:
→
−
−−−→
L = const.
(3.61)
W przypadku tym więc moment pędu jest stałym wektorem. Stwierdzenie to
wyraża zasadę zachowania momentu pędu.
−
→
Warunek znikania momentu siły M = 0 pociąga ze sobą stałość momentu pędu.
Mamy więc wtedy do czynienia z ruchem płaskim stale odbywającym się w płaszczy→
− −−−→
źnie prostopadłej do wektora L =const..
−
→ − →
−
Warunek znikania momentu siły M = →
r × F = 0 może być spełniony w dwóch
→
−
→
− −
przypadkach, gdy F = 0 lub gdy wektory F i →
r są do siebie równoległe. Pierwszy
z tych przypadków to przypadek, gdy nie ma oddziaływań, drugi to przypadek,
gdy działa siła centralna. Siły centralne to siły o postaci:
→
−
r
→
−
(3.62)
F = Fr .
r
52
Dynamika punktu materialnego
→
−
→
−
→
−
−
Siły centralne to np. siła sprężysta F = -k→
r , siła grawitacji F =− rκ2 rr , itp.
→
−
−
−
Gdy moment pędu L = →
r × m→
v jest stałym wektorem, to wtedy także
prędkość polowa cząstki
→
−
1
L
1
→
−
−
−
σ = →
r ×→
v =
(3.63)
2
2m
jest stała.
3.6
Wzór Bineta
Wzór Bineta pozwala znaleźć postać działającej siły centralnej:
→
−
r
→
−
F = Fr ,
r
(3.64)
gdy znane jest równanie toru cząstki.
→
− −−−→
Gdy działa siła centralna moment pędu jest stałym wektorem L =const., a
stąd wynika, że ruch odbywa się stale w tej samej płaszczyźnie. Z symetrii problemu wynika, że najwygodniej, gdy równanie toru wyrażone jest we współrzędnych
biegunowych:
r = r(ϕ).
(3.65)
W układzie współrzędnych biegunowych prędkość można rozłożyć na dwie składowe radialną vr i transwersalną vϕ . Stąd także moment pędu ma dwie składowe:
→
−
→
−
→
−
L = L r + L ϕ.
(3.66)
→
−
−
−
−
−
Jednak składowa radialna L r = →
r × m→
vr = 0, ponieważ wektory →
r i →
vr są
do siebie równoległe i cały wkład do momentu pędu związany jest ze składową
transwersalną prędkości:
L = Lϕ = rmvϕ = mr2 ϕ̇ = const.
(3.67)
→
−
−
Dla siły centralnej istnieje tylko składowa radialna przyspieszenia F = m→
ar , gdzie
→
−
a r = r̈ − rϕ̇2. Stąd dla siły centralnej mamy:
Fr = m(r̈ − rϕ̇2).
(3.68)
Z równania tego możemy znaleźć postać działającej siły centralnej, gdy znamy
równania ruchu cząstki r=r(t) i ϕ = ϕ(t). Aby otrzymać wzór Bineta trzeba z
tego równania wyeliminować pochodne po czasie.
3.6 Wzór Bineta
53
Pochodną ϕ̇ można znaleźć z równania (3.67):
L
.
(3.69)
mr2
Różniczkowanie po czasie w wyrażeniu r̈ należy zastąpić różniczkowaniem po zmiennej ϕ:
ϕ̇ =
dr dϕ
L dr
L d 1
ṙ =
=
=
−
dϕ dt
mr2 dϕ
m dϕ r
!
(3.70)
i dalej można pokazać, że
!
dṙ dϕ
L2 d 2 1
r̈ =
=− 2 2 2
.
dϕ dt
m r dϕ r
(3.71)
W rezultacie równanie (3.67) przybiera postać wzoru Bineta:
!
!
L2 d 2 1
1
Fr = − 2
+
.
mr dϕ2 r
r
(3.72)
Znając równanie toru r = r(ϕ) możemy ze wzoru Bineta znaleźć postać siły centralnej, która działa na poruszający się punkt materialny.
Także odwrotnie, jeśli znana jest postać działającej siły ze wzoru (3.72) wyznaczyć można tor ruchu. Dalej znając równanie ruchu ϕ = ϕ(t), które otrzymuje
się po scałkowaniu równania L = mr 2 ϕ̇, z równania toru r = r(ϕ) można otrzymać
drugie równanie ruchu r=r(t).
Przykład - zastosowanie wzoru Bineta
Punkt materialny o masie m porusza się pod wpływem siły centralnej po torze w
kształcie okręgu o promieniu R i o środku w początku układu współrzędnych. Jak
zależy wartość tej siły od odległości punktu od centrum?
Równanie toru punktu materialnego w układzie współrzędnych biegunowych
ma postać:
r = R,
(3.73)
gdzie R = const.. Ze wzoru Bineta mamy:
L2
,
mR3
gdzie L = mRv. Ostatecznie otrzymujemy
Fr = −
mv 2
.
R
Działająca siła ma więc postać siły dośrodkowej.
Fr = −
(3.74)
(3.75)
54
Dynamika punktu materialnego
3.7
Praca, moc, energia kinetyczna
−
Pomnóżmy skalarnie obie strony równania Newtona przez wektor przesunięcia d →
r
−
d→
p
→
− −
−
· d→
r = F · d→
r
(3.76)
dt
Praca
Rozpoczniemy analizę uzyskanego równania (3.76) od strony prawej. Występujący
tam iloczyn skalarny oznaczmy przez dW .
→
− −
dW = F · d→
r
(3.77)
→
−
−
Jest to praca siły F przy przesunięciu d→
r . Analityczna forma tego iloczynu
skalarnego jest następująca:
dW = Fx dx + Fy dy + Fz dz.
(3.78)
Iloczyn skalarny dW, to liczba, którą oblicza się następująco:
→
−
−
dW = | F | · |d→
r | cos θ.
(3.79)
→
−
W zależności od kąta zawartego pomiędzy wektorem siły F , a wektorem prze−
sunięcia d→
r , praca może być liczbą dodatnią, ujemną lub zerem. Mianowicie dla
kąta:
0<θ< π2 praca jest dodatnia
θ= π2 praca jest zerowa
π
2 =θ=π
praca jest ujemna
→
−
−
θ = 0 wartość pracy jest maksymalna dW = | F | · |d→
r |.
Wartość pracy zależy od składowej stycznej siły Ft:
Składową Ft oblicza się następująco:
→
−
Ft = | F | · cos θ.
Zatem praca dW to iloczyn składowej stycznej siły i elementu drogi ds:
→
−
−
dW = | F | · |d→
r | cos θ = Ft · ds,
(3.80)
(3.81)
3.7 Praca, moc, energia kinetyczna
55
−
ponieważ dla nieskończenie małego przesunięcia |d→
r |=ds.
→
−
Praca siły F na drodze L pomiędzy punktami A i B wyraża się przez całkę:
Z B
→
− →
WAB =
F · d−
r.
(3.82)
A(L)
→
−
Pracę siły F można też obliczyć z wyrażenia:
WAB =
Z B
A(L)
Ft · ds.
(3.83)
Wartość tej całki jest polem powierzchni pod krzywą na wykresie
zależności Ft od s:
W ogólności praca zależy od kształtu drogi L pomiędzy punktami A i B
Z B
A(L1 )
Ft · ds 6=
Z B
A(L2 )
Ft · ds.
(3.84)
Moc
Z pojęciem pracy wiąże się pojęcie mocy. Moc wskazuje na szybkość wykonywania
pracy:
P =
dW
.
dt
(3.85)
→
− −
Ponieważ dW= F ·d→
r , to moc można zdefiniować jako następujący iloczyn skalarny:
→
− −
P = F ·→
v.
(3.86)
56
Dynamika punktu materialnego
Znajomość mocy jako funkcji czasu pozwala obliczyć pracę siły:
W =
Z t
2
t1
P (t)dt.
(3.87)
3.7 Praca, moc, energia kinetyczna
57
Energia kinetyczna
Powróćmy do wyrażenia (3.76). Przeanalizujemy teraz lewą stronę tego równania
tzn. wyrażenie:
−
−
d→
p
d→
v
→
−
−
−
−
·dr =m
· d→
r = m→
v · d→
v = mv dv.
(3.88)
dt
dt
W powyższym przekształceniu przyjęliśmy, że masa punktu materialnego nie zmienia
się w czasie.
Wyrażenie (3.76) możemy więc zapisać następująco:
mv dv = dW
(3.89)
Po scałkowaniu obu stron równania (3.89)
m
otrzymujemy
Z v
B
vA
vdv =
Z B
A(L)
dW
(3.90)
1
1 2
mvB − mvA2 = WAB
(3.91)
2
2
Wielkość 12 mv 2 nazywamy energią kinetyczną i oznaczamy Ek .
1
Ek = mv 2 .
(3.92)
2
−
Energia kinetyczna jest energią ruchu - każde ciało poruszające się z prędkością →
v
posiada energię kinetyczną Ek . Wzór (3.91) oznacza, że niezależnie od postaci siły
→
−
F , czy też kształtu drogi przebytej przez cząstkę, praca W AB tej siły jest zawsze
równa różnicy energii kinetycznej Ek obliczonej na końcu B i na początku A drogi
L.
Przykład - praca siły sprężystej przy przesunięciu wzdłuż promienia
→
−
−
−
Obliczamy pracę siły sprężystej F =-k→
r przy przesunięciu wzdłuż promienia →
r
od punktu A(0, 0, 0) do punktu B(x, y, z). Z równania (3.82) mamy:
k 2
kr2
2
2
W = −k x dx − k y dy − k z dz− = − (x + y + z ) = −
. (3.93)
0
0
0
2
2
Możemy też użyć tu drugiego sposobu obliczeń. Jeśli przesunięcie odbywa się
wzdłuż promieni to siła sprężysta posiada tylko składową styczną F t =-kr. Z równania (3.83) mamy:
Z r
kr2
W = −k rdr = −
.
(3.94)
0
2
Na wykresie zależności składowej Ft siły od s wartość tej całki jest równa polu
trójkąta o wysokości kr i postawie r.
Z x
Z y
Z z
58
3.8
Dynamika punktu materialnego
Siły zachowawcze
−
−
W ogólności siła może być funkcją położenia →
r , prędkości →
v i czasu t. Rozpatrzmy
→
− →
− →
−
przypadek, kiedy F = F ( r ) tzn. kiedy działanie siły odbywa się poprzez pole
siłowe. Wśród tych sił istnieją takie, dla których całka
Z B
→
− →
F · d−
r = WAB
(3.95)
A(L)
przybiera tą samą wartość niezależnie od wyboru drogi L łączącej punkty A i B
→
−
→
−
pola siłowego. Taką własność mają na przykład siły centralne F =Fr rr . Łatwo to
sprawdzić analizując sytuację przedstawioną poniżej.
−→
−
→
Porównajmy pracę dW1, wykonaną przez siłę F1 przy przesunięciu dr1 na drodze
−→
−
→
L1 i pracę dW2 wykonaną przez siłę F2 przy przesunięciu dr2 na drodze L2 :
dW1 = F1 dr1 cos θ1
dW2 = F2 dr2 cos θ2.
(3.96)
−
→ −
→
W punktach M i N pola siły F1 i F2 mają taką samą wartość - punkty te są równo
oddalone od centrum działania siły:
F1 = F2 = F.
(3.97)
Ponadto
dr1 cos θ1 = dr
dr2 cos θ2 = dr.
(3.98)
3.8 Siły zachowawcze
59
Widzimy więc, że prace dW1 i dW2 są sobie równe:
dW1 = dW2 = F dr.
(3.99)
Przedstawioną analizę można powtórzyć dla kolejnych elementów dróg L 1 i L2 .
→
− →
− −
Siła zachowawcza, to siła postaci F = F (→
r ), dla której całka
Z B
A(L)
→
− →
F · d−
r
(3.100)
zależy tylko od wyboru punktu początkowego A i końcowego B, a nie zależy od
wyboru drogi L łączącej punkty A i B.
Z definicji pracy jako całki oznaczonej wynika, że
WAB = −WBA .
(3.101)
Stąd warunek, który musi spełnić siła zachowawcza można też sformułować następująco:
I
→
− →
F · d−
r = 0.
(3.102)
Jeśli cząstka przebywa drogę zamkniętą w polu siłowym, to praca siły zachowawczej
jest równa zeru.
Energia potencjalna
→
− −
Dla sił zachowawczych wyrażenie F · d→
r występujące pod całką we wzorze (3.95)
−
możemy zapisać jako różniczkę zupełną pewnej funkcji skalarnej E p = Ep(→
r).
→
− −
dW = F · d→
r = −dEp .
(3.103)
−
−
Ep(→
r ) nazywamy energią potencjalną cząstki w położeniu →
r w polu siły zachowawczej. Wyrażenie (3.103) przedstawia sens fizyczny tego pojęcia - praca
wykonana przez siłę pola odbywa się kosztem ubytku energii potencjalnej zgromadzonej w polu. Praca siły pola równa jest różnicy energii potencjalnej obliczonej
w punkcie początkowym i końcowym działania siły:
−
Z →
r →
− →
−
−
F · d−
r = −Ep (→
r ) + Ep (→
r0 ).
(3.104)
W =− →
−
r0
→
− −
Dla siły zachowawczej całka F · d→
r zależy tylko od wyboru punktu początkowego
i końcowego. Jeśli jednak ustalimy punkt początkowy to wartość tej całki zależy
60
Dynamika punktu materialnego
tylko od wyboru punktu końcowego (całka jest jedynie funkcją górnej granicy
całkowania). W ten sposób każdemu punktowi pola siły zachowawczej możemy
przypisać liczbę zależną tylko od położenia punktu - pole skalarne:
−
Z →
Z
r →
− →
→
− →
→
−
−
→
−
Ep ( r ) = − →
F
·
d
r
+
E
(
r
)
=
−
F · d−
r + const..
(3.105)
p 0
−
r0
−
Widzimy więc, że energia potencjalna Ep (→
r ) jest zawsze określona z dokładnością
−
do pewnej addytywnej, zależnej od wyboru punktu odniesienia →
r0 . Ta niejednoznaczność w określeniu energii potencjalnej wynika z tego, że pojęcie to jest konstrukcją matematyczną, która nie ma sensu fizycznego. Sens fizyczny jako praca
−
−
sił pola ma jedynie różnica energii potencjalnej Ep(→
r ) − Ep(→
r0 ).
Na podstawie wzoru
Z
→
−
E ( r ) = − (F dx + F dy + F dz) + const.,
(3.106)
p
x
y
z
−
każdemu punktowi pola siłowego można przypisać wielkość skalarną E p(→
r ). Można
→
−
też postąpić odwrotnie. Jeśli znane jest pole skalarne E p( r ), to możemy znaleźć
→
− −
pole wektorowe F (→
r ) w następujący sposób:
−−→
−
→
F = −grad Ep
(3.107)
→
−
Gradient funkcji skalarnej obliczamy posługując się operatorem różniczkowym ∇,
którego składowe to pochodne cząstkowe:
∂
∂
∂
→
−
∇ = xb
+ yb + zb .
(3.108)
∂x
∂y
∂z
Równanie (3.107) ma więc następującą postać:
∂Ep
∂Ep
∂Ep
→
−
→
−
F = − ∇Ep = −(xb
+ yb
+ zb
).
(3.109)
∂x
∂y
∂z
→
−
Jeśli f jest pewną funkcją skalarną, to ∇f jest wektorem charakteryzującym zmi→
−
enność funkcji w otoczeniu punktu. Kierunek wektora ∇f jest kierunkiem na∂f
jszybszego wzrostu funkcji f , bo ∂x
określa szybkość z jaką zmienia się funkcja
i
wraz ze zmianą współrzędnej xi.
→
−
Szczególnie łatwo oblicza się ∇f , jeśli funkcja skalarna jest tylko funkcją r.
Wtedy
−
df →
r
→
−
∇f (r) =
.
(3.110)
dr r
Zależność (3.110) można wyprowadzić korzystając z tego, że df jest różniczką
zupełną:
∂f
∂f
∂f
∂f
∂f
∂f
b
b
b
df =
dx +
dy +
dz = (xb
+ yb
+ zb ) · (xdx
+ ydy
+ zdz)
∂x
∂y
∂z
∂x
∂y
∂z
→
−
r
→
−
→
−
→
−
= ∇f · d r = dr ∇f · .
(3.111)
r
3.8 Siły zachowawcze
61
Dzieląc obie strony otrzymanej równości przez dr otrzymujemy związek (3.110).
Przykład - energie potencjalne kilku sił centralnych
Za pomocą wzoru
−
Ep (→
r)=−
Z
→
− →
F · d−
r + const.,
(3.112)
każdemu punktowi pola siłowego można przypisać wielkość skalarną - energię potencjalną.
→
−
→
−
(1) Poszukujemy energii potencjalnej dla siły sprężystej F = −kr rr
kr2
+ const.,
(3.113)
2
→
−
(2) Energia potencjalna dla siły postaci F = − rκ2 rr (może to być siła grawitacji
lub też siła Coulomba).
Ep(r) = k
Z
Ep(r) = κ
Z
rdr + const. =
κ
dr
+
const.
=
−
+ const.,
r2
r
(3.114)
Przykład - gradient funkcji skalarnej f(r)=r
→
−
→
−
Obliczamy najpierw ∇r, korzystając z definicji operatora ∇
√
gdzie r = x2 + y 2 + z 2 .
Ponieważ
∂r
x
= ,
∂x
r
∂r
∂r
∂r
→
−
∇r = xb
+ yb + zb ,
∂x
∂y
∂z
∂r
y
= ,
∂y
r
(3.115)
∂r
z
= ,
∂z
r
(3.116)
mamy
→
−
1
r
→
−
b + yy
b + zz)
b
∇r = (xx
= .
r
r
Gradient r można też obliczyć ze wzoru (3.110). Otrzymujemy
−
→
−
dr →
r
r
→
−
∇r =
= .
dr r
r
(3.117)
(3.118)
62
Dynamika punktu materialnego
Zasada zachowania całkowitej energii mechanicznej
Wiemy, że każdemu punktowi pola wokół źródła siły zachowawczej można przypisać wielkość skalarną zwaną energią potencjalną. Aby przesunąć punkt materialny
z jednego punktu pola do drugiego siły pola muszą wykonać pracę:
dW = −dEp .
(3.119)
dW = dEk .
(3.120)
Z drugiej strony otrzymaliśmy:
Praca sił pola powoduje przyrost energii kinetycznej punktu materialnego. Zatem
dla sił zachowawczych otrzymujemy:
d(Ek + Ep) = 0.
(3.121)
Sumę Ek + Ep = E nazywamy całkowitą energią mechaniczną. Jest to jak widać
wielkość zachowana
E = Ek + Ep = const.
(3.122)
Równanie (3.122) wyraża zasadę zachowania całkowitej energii mechanicznej : podczas ruchu pod działaniem siły zachowawczej całkowita energia mechaniczna pozostaje stała. Stąd też pochodzi nazwa siły zachowawcze lub konserwatywne - są
to siły zachowujące energię mechaniczną.
Siły konserwatywne nie mogą zależeć od prędkości, bo dla nich nie istnieje
→
−
−
−
funkcja skalarna Ep(→
r ). Jeśli jednak siła F zależy od →
v w ten sposób, że jest do
→
− →
tego wektora prostopadła, to iloczyn skalarny F · −
v = 0, a także praca siły W = 0.
Wówczas siła mimo, że nie jest zachowawcza nie powoduje naruszenia zasady zachowania całkowitej energii mechanicznej. Siły prostopadłe do wektora prędkości
nazywa się siłami giroskopowymi. Przykładem takiej siły jest siła Lorentza, działa→
−
→
−
−
jąca na naładowaną cząstkę w polu magnetycznym F = q(→
v × B ). Innym przykła→
−
−
−
dem jest tzw. siła Coriolisa należąca do sił bezwładności F = −2m(→
ω ×→
v 0 ).
−
Siła ta działa na ciało poruszające się z prędkością →
v 0 w nieinercjalnym układzie
−
odniesienia, który jest w ruchu obrotowym z prędkością →
ω.
Inne siły występujące w przyrodzie zależne od prędkości nie są siłami zachowawczymi i prowadzą do rozproszenia energii mechanicznej. Są one związane
z tarciem lub lepkością ośrodka. Siły takie nazywamy dysypatywnymi (rozpraszającymi). W przypadku działania tych sił energia mechaniczna przechodzi w inne
3.9 Zagadnienie Keplera
63
formy energii. Na przykład w przypadku działania sił tarcia energia mechaniczna
przemienia się w energię nieuporządkowanego ruchu atomów i cząsteczek ośrodka.
Tak więc na poziomie mikroskopowym energia jest zawsze zachowana, ginie tylko
ta forma energii, która jest związana z ruchem ciał makroskopowych.
Zasada zachowania energii jest obok zasady zachowania pędu i zasady zachowania momentu pędu trzecią z zasad zachowania mechaniki. Okazuje się, że zasady
zachowania związane są z pewnymi symetriami przestrzeni i czasu. Stanowi to
treść fundamentalnego twierdzenia fizyki teoretycznej tzw. twierdzenia Noether.
Matematyczka niemiecka Emma Noether sformułowała to twierdzenie w 1918r.
Według niego zasada zachowania pędu ma związek z jednorodnością przestrzeni,
tzn. z tym, że każdy punkt przestrzeni jest taki sam, nie ma punktów wyróżnionych.
Zasada zachowania momentu pędu ma związek z izotropowością przestrzeni. Żaden
kierunek w przestrzeni nie jest wyróżniony. Zaś zasada zachowania energii ma
związek z jednorodnością czasu. Każda chwila czasu jest równoważna i przebieg
zjawiska nie zależy od wyboru chwili początkowej i końcowej.
3.9
Zagadnienie Keplera
Poszukujemy toru cząstki poruszającej się w polu siły centralnej o postaci:
−
κ→
r
→
−
F =− 2 ,
κ > 0.
(3.123)
r r
Zagadnienie Keplera można rozwiązać posługując się wzorem Bineta. Jednak
otrzymane rozwiązanie - równanie toru r = r(ϕ), zależy od całkowitej energii mechanicznej cząstki. Aby dokonać analizy otrzymanego rozwiązania ze względu na
wartość energii mechanicznej lepiej przy rozwiązaniu zagadnienia Keplera posłużyć
się energetycznym wzorem Bineta.
Energetyczny wzór Bineta
Punktem wyjścia do wyprowadzenia wzoru Bineta było równanie Newtona:
→
−
−
F = m→
a,
(3.124)
dla siły centralnej, wyrażone we współrzędnych biegunowych.
Siła centralna jest zachowawcza; polu siłowemu odpowiada pole skalarne E p =
Ep(r). Punktem wyjścia do wyprowadzenia energetycznego wzoru Bineta jest równanie
mv 2
E=
+ Ep(r) = const.
(3.125)
2
64
Dynamika punktu materialnego
Równanie to wyraża zasadę zachowania całkowitej energii mechanicznej dla siły
zachowawczej.
W układzie współrzędnych biegunowych wektor prędkości ma składowe radialną i transwersalną:
v 2 = vr2 + vϕ2 = ṙ2 + r2ϕ̇2 .
(3.126)
Aby otrzymać z równania (3.125) poszukiwane równanie różniczkowe na tor ruchu
cząstki r = r(ϕ) trzeba z tego wyrażenia wyeliminować pochodne po czasie i
zastąpić je pochodnymi po ϕ. Już uprzednio przy wyprowadzeniu wzoru Bineta
otrzymaliśmy:
!
L d 1
ṙ = −
.
m dϕ r
L
ϕ̇ =
,
mr2
(3.127)
Wstawiając te pochodne do wzoru (3.125) otrzymujemy:
L2
E=
2m
"
d 1
dϕ r
!!2
#
1
+ 2 + Ep(r).
r
(3.128)
Jest to poszukiwany wzór, z którego jeśli znamy postać energii potencjalnej w
polu siłowym można wyznaczyć tor ruchu cząstki. Jest to równanie różniczkowe
pierwszego rzędu, podczas gdy wzór Bineta przedstawia równanie drugiego rzędu.
Rozwiązanie zagadnienia Keplera
Energia potencjalna pola siłowego (3.123) ma postać:
κ
Ep = − ,
κ>0
r
Poszukujemy więc rozwiązania następującego równania różniczkowego:
L2
E=
2m
"
d 1
dϕ r
!!2
#
1
κ
+ 2 − .
r
r
(3.129)
(3.130)
Jak widać całkowita energia mechaniczna cząstki to różnica dwóch wkładów. E
może być liczbą dodatnią, ujemną lub równą zeru. Wartość E pozostaje stała w
czasie ruchu. Wprowadzimy oznaczenie µ = 1r . Wtedy:
L2
E=
2m
"
dµ
dϕ
!2
+µ
2
#
− κµ.
(3.131)
Równanie to daje się scałkować przez rozdzielenie zmiennych. Jednak dogodniej
jest zróżniczkować względem ϕ jego obie strony. Otrzymujemy wtedy:
!
L2 d 2 µ
+µ −κ=0
m dϕ2
(3.132)
3.9 Zagadnienie Keplera
65
oraz
!
d2 µ
κm
+
µ
−
= 0.
dϕ2
L2
Ponieważ
κm
L2
(3.133)
to stała, więc równanie (3.133) można zapisać następująco:
!
!
d2
κm
κm
µ
−
+
µ
−
= 0.
dϕ2
L2
L2
(3.134)
Jest to analog równania oscylatora harmonicznego dla zmiennej ϕ (ẍ + ω 2x = 0,
gdzie ω = 1, którego rozwiązanie może być zapisane w formie x = A cos(ωt − γ)).
Wobec tego możemy przyjąć, że rozwiązanie równania (3.134) ma postać:
µ−
κm
= h cos(ϕ − γ),
L2
(3.135)
gdzie h i γ są stałymi dowolnymi.
Powracając do zmiennej r mamy:
1 κm
= 2 + h cos(ϕ − γ))
r
L
(3.136)
oraz
r=
gdzie przyjęliśmy oznaczenia:
p
,
1 + ε cos(ϕ − γ)
L2
p=
,
κm
hL2
ε=
.
κm
(3.137)
(3.138)
Otrzymane w układzie współrzędnych biegunowych równanie toru to równanie
krzywej stożkowej o mimośrodzie ε i parametrze p. W zależności od wartości ε
krzywa ta przedstawia: hiperbolę(ε > 1), parabolę (ε = 1), elipsę (ε < 1) lub
okrąg (ε = 0). Możliwy jest także ruch po prostej, jeśli p=0.
Rozwiązanie (3.136) to tzw. całka ogólna równania różniczkowego (3.130). Aby
znaleźć całkę szczególną trzeba z warunków początkowych wyznaczyć stałe h i γ.
66
Dynamika punktu materialnego
Stałą h znajdujemy wstawiając rozwiązanie (3.136) do równania (3.130). Otrzymujemy wtedy:
E=
h 2 L2 1 κ 2 m
−
.
2m
2 L2
(3.139)
Zatem
v
u
κm u
2L2E
t
h= 2 1+ 2 .
L
κm
(3.140)
Jeśli przyjąć warunek początkowy tak, by w chwili t = 0 cząstka znajdowała
się w najmniejszej możliwej odległości od centrum działania siły (ϕ(0) = 0 oraz
r(0) = rmin ), to wtedy γ = 0. Ostatecznie więc jako rozwiązanie zagadnienia
Keplera otrzymujmy następujące równanie toru cząstki:
p
,
(3.141)
r=
1 + ε cos ϕ
gdzie
p=
2
L
,
κm
ε=
v
u
u
t
1+
2L2E
.
κ2 m
(3.142)
Cząstki o jednakowej masie i jednakowym momencie pędu L lecz o różnych energiach E poruszają się po różnych orbitach względem centrum siły. Gdy E > 0
(ε > 1) mamy ruch po hiperboli, gdy E = 0 (ε = 1) mamy ruch po paraboli, a
gdy E < 0 (ε < 1) ciało porusza się po elipsie - orbita zamyka się i ciało nie może
oddalić się do nieskończoności.
Dyskusja rozwiązania zagadnienia Keplera
W dyskusji nad rozwiązaniem zagadnienia Keplera przydaje się pojęcie efektywnej
energii potencjalnej. Pojęcie to pozwala przedyskutować warunki na przejście od
orbit otwartych do zamkniętych.
Równanie ruchu w nieinercjalnym układzie odniesienia związanym z cząstką
poruszającą się po torze krzywoliniowym ma następującą postać:
κ
mẍ = mω 2 r − 2 .
(3.143)
r
Widzimy więc w tym układzie działanie dwóch sił. Jedna z tych sił, siła centralna,
o wartości rκ2 ma charakter przyciągający. Siła ta konkuruje z drugą, skierowaną na
zewnątrz wzdłuż promienia siłą bezwładności mω 2 r. W nieinercjalnych układach
odniesienia pojawiają się siły bezwładności, o których będzie mowa w następnych
3.9 Zagadnienie Keplera
67
rozdziałach. Jedną z tych sił, która pojawia się w układzie odniesienia wykonującym ruch obrotowy jest siła odśrodkowa bezwładności. Siła ta ma taką samą
wartość:
mv 2
= mω 2 r,
Fd =
r
(3.144)
jak występująca w każdym ruchu krzywoliniowym, w układzie inercjalnym, siła
dośrodkowa Fd .
Sile efektywnej
κ
Fef = mω 2 r − 2 ,
(3.145)
r
można przypisać efektywną energię potencjalną:
Ep,ef = −
Z
!
κ
mω r − 2 dr + const..
r
2
(3.146)
W wyrażeniu pod całką ω nie jest stałą, ale ponieważ siła centralna zachowuje
moment pędu L mamy:
L
ω = ϕ̇ =
,
(3.147)
mr2
oraz
Ep,ef = −
Z
!
L2
κ
−
dr,
mr3 r2
(3.148)
gdzie przyjęliśmy, ze stała addytywna z jaką określa się energię potencjalną wynosi
zero. Wyrażenie (3.148) można teraz scałkować. Otrzymujemy:
Ep,ef
L2
κ
=
−
.
2mr2 r
(3.149)
Efektywna energia potencjalna zawiera różnicę dwóch wkładów. Pierwszy z nich,
L2
zawsze dodatni mr
2 , to energia potencjalna siły odśrodkowej, drugi to energia
potencjalna siły centralnej. Przebieg zależności efektywnej energii potencjalnej
jako funkcji r przedstawia poniższy rysunek:
Na rysunku pokazane są również krzywe energii potencjalnej dwóch konkurencyjnych sił odpychającej i przyciągającej. Efektywna energia potencjalna osiąga
L2
wartość minimalną w punkcie r0= mκ
. Łatwo sprawdzić, że w tym punkcie Ep,ef =
1κ
− 2 r0 .
68
Dynamika punktu materialnego
Porównajmy wyrażenie na efektywną energię potencjalną z energetycznym wzorem
Bineta. Otrzymujemy:
L2 d 1
E=
2m dϕ r
!!2
+ Ep,ef .
(3.150)
Pierwszy wyraz po prawej stronie wyrażenia (3.150) to wkład pochodzący od
energii kinetycznej związany z prędkością radialną. Wyraz ten jest zawsze dodatni
(lub równy zeru). Widzimy więc, że całkowita energia mechaniczna nie może być
mniejsza od minimalnej wartości Ep,ef ; E ­ Ep,ef .
Kiedy odległość cząstki od centrum działania siły jest najmniejsza (lub najwięk−
sza), wtedy wektor prędkości jest prostopadły do →
r - składowa radialna prędkości
znika i wtedy E = Ep,ef . Zachodzi to dla tzw. punktów zwrotnych toru.
Całkowitą energię mechaniczną można przedstawić na wykresie zależności E p,ef =
Ep,ef (r) jako linię poziomą, która zawsze musi przecinać się z krzywą efektywnej
energii potencjalnej. W zależności od wartości E możemy otrzymać jeden lub dwa
punkty przecięcia się krzywych. Punkty przecięcia się tych krzywych wyznaczają
punkty zwrotne, pomiędzy którymi zawarty jest możliwy obszar ruchu. Następujące cztery rysunki przedstawiają możliwe tory ruchu cząstki w polu siły centralnej
→
−
→
−
F = − rκ2 rr :
(a) E > 0 - jeden punkt zwrotny - ruch po hiperboli
(b) E = 0 - jeden punkt zwrotny - ruch po paraboli
(c) E < 0 - dwa punkty zwrotne - ruch po elipsie
3.10 Prawa Keplera
69
(d) E = Ep,ef (r0) = − 21 κr - jeden punkt zwrotny - ruch po okręgu.
3.10
Prawa Keplera
Na więcej niż pół wieku przed odkryciem praw mechaniki przez Newtona, niemiecki
astronom i matematyk Johannes Kepler sformułował, w serii prac, trzy prawa
70
Dynamika punktu materialnego
ruchu planet, bazując w znacznie mierze na obserwacjach astronomicznych prowadzonych latami przez duńskiego astronoma Tycho Brahe. Kepler był współpracownikiem Brahe w ostatnich latach życia astronoma. Wyjaśnienie przez Newtona na
gruncie mechaniki klasycznej praw Keplera było jednym z największych osiągnięć
fizyki w historii.
Przedstawimy teraz kolejno trzy prawa ruchu planet wraz z ich wyjaśnieniem
za pomocą praw mechaniki klasycznej.
Pierwsze prawo Keplera
Każda planeta krąży wokół Słońca po elipsie, a Słońce znajduje się w jednym z
ognisk elipsy.
Z rozwiązania zagadnienia Keplera wynika, że elipsa jest jednym z możliwych
→
−
torów ruchu w polu siły centralnej o postaci F = − rκ2 rr . Taki tor ruchu występuje, kiedy całkowita energia mechaniczna E < 0. Odpowiada to sytuacji, kiedy
energia potencjalna poruszającego się ciała przeważa nad jego energią kinetyczną.
Równanie elipsy we współrzędnych biegunowych ma postać:
p
r=
,
(3.151)
1 + ε cos ϕ
gdzie otrzymaliśmy:
p=
2
L
,
κm
ε=
v
u
u
t
1−
2L2|E|
κ2 m
(3.152)
Wyrażenie na ε uwzględnia fakt, że elipsa może być torem ruchu, jeśli E < 0.
3.10 Prawa Keplera
71
Drugie prawo Keplera
Promień wodzący każdej planety zakreśla równe pola w równych odstępach czasu;
prędkość polowa każdej z planet jest stała.
Stałość prędkości polowej wskazuje na to, że siła odpowiedzialna za ruch ciała
→
−
→
−
−
→
jest siłą centralną F = Fr rr Jeśli działa siła centralna, to jej moment M =
→
−
→
−
r × F = 0 . Z drugiej zasady dynamiki dla ruchu obrotowego:
→
−
−
→ dL
M=
,
dt
(3.153)
−
→
→
−
−−−→
wynika, że kiedy M = 0, wtedy L = const. - ruch odbywa się w ustalonej
→
−
płaszczyźnie ruchu. Pomiędzy prędkością polową, a momentem pędu L istnieje
następujący związek:
→
−
L
→
−
.
σ =
2m
(3.154)
Ze stałości momentu pędu wynika więc stałość prędkości polowej.
Trzecie prawo Keplera
Kwadrat okresu obiegu każdej planety wokół Słońca jest proporcjonalny do sześcianu półosi wielkiej elipsy.
Najpierw parę informacji o elipsie. Elipsa to miejsce geometryczne punktów
jednakowo odległych od ognisk elipsy. Oznacza to, że suma odległości ON i O’N
dla dowolnego punktu N na obwodzie elipsy jest stała. Odcinki a i b to odpowiednio
półoś wielka i mała elipsy. Pole powierzchni elipsy wynosi πab. Mimośród elipsy
2
to stosunek odległości c do a; ε = ac , a parametr p = ba jest wartością rzędnej
punktu M (patrz rysunek).
72
Dynamika punktu materialnego
Ruch po elipsie jest ruchem periodycznym. Obliczmy okres T tego ruchu korzystając ze stałości prędkości polowej:
dS
σ=
,
dt
Z πab
0
dS = σ
Z T
0
dt.
(3.155)
Mamy więc:
πab =
L
T.
2m
(3.156)
Stąd dalej:
4π 2 m2 a2 b2
4π 2 m2 3 4π 2 m 3
=
pa =
a.
(3.157)
L2
L2
κ
Otrzymujemy więc poszukiwaną zależność T 2 ∼ a3 .
Pokażemy jeszcze, że półoś wielka elipsy zależy wyłącznie od wartości całkowitej
energii mechanicznej |E|. Zauważmy, że:
p
p
rmin = r(ϕ = 0) =
,
rmax = r(ϕ = π) =
.
(3.158)
1+ε
1−ε
Suma odległości rmin i rmax , to podwojona długość półosi wielkiej elipsy:
T2 =
rmin + rmax = 2a.
(3.159)
p
p
+
= 2a,
1+ε 1−ε
(3.160)
Mamy więc:
a stąd
a=
p
.
1 − ε2
(3.161)
Podstawiając za p i ε otrzymane uprzednio wyrażenia (3.152) otrzymujemy:
κ
a=
.
(3.162)
2|E|
Otrzymaliśmy więc poszukiwany wzór, który pokazuje, że energia ruchu po elipsie
zależy wyłącznie od jej półosi wielkiej.
3.11
Newtonowskie prawo ciążenia powszechnego
Na podstawie doświadczalnych praw Keplera, Newton wyciągnął wniosek, że siła
działająca pomiędzy planetami Układu Słonecznego a Słońcem ma postać:
mM
→
−
F ∝ 2 ,
r
(3.163)
3.11 Newtonowskie prawo ciążenia powszechnego
73
Według Newtona ta sama siła musi być odpowiedzialna za ciężar ciał na Ziemi.
Ponieważ spadające swobodnie ciała ulegają przyspieszeniu musi na nie działać
stała w czasie siła grawitacji. Newton spostrzegł, że siła grawitacji zależy nie
tylko od odległości pomiędzy ciałami, ale także od masy ciała. Siła oddziaływania
pomiędzy ciałami powinna być symetryczna w tym sensie, że jeśli jedno z ciał
działa na drugie siłą zależną od masy to, to drugie ciało musi działać na pierwsze taką samą siłą - stąd wielkość oddziaływania pomiędzy masami musi być
proporcjonalna do iloczynu mas obu ciał.
Prawo ciążenia powszechnego można wyrazić następująco:
Ciała w przestrzeni oddziałują pomiędzy sobą siłami grawitacji, które są proporcjonalne do iloczynu mas obu ciał, a odwrotnie proporcjonalne do kwadratu
odległości pomiędzy nimi. Siła oddziaływania działa wzdłuż linii łączącej oba ciała.
Prawo ciążenia powszechnego można więc zapisać następująco:
−
mM →
r
→
−
F =G 2
,
r r
(3.164)
gdzie G nosi nazwę stałej grawitacji. Stała ta pełni dwojaką rolę w równaniu
(3.164). Po pierwsze pozwala na dopasowanie jednostek wielkości fizycznych, które
występują po lewej i prawej stronie wyrażenia. Po drugie skaluje oddziaływanie.
Wartość stałej G jest bardzo mała, dlatego jej wartość po raz pierwszy wyznaczono doświadczalnie po około 100 latach po opublikowaniu przez Newtona prawa
ciążenia powszechnego. Aby wyznaczyć stałą G trzeba w eksperymencie dokonać
dokładnego pomiaru kilku wielkości: F , M , m i r. Udało się tego dokonać po raz
pierwszy Henremu Cavendishowi, który w doświadczaniu użył, tzw. wagi skręceń.
Wartość G wynosi:
G ≈ 6.67 · 10−11
N m2
.
kg 2
(3.165)
Oddziaływanie grawitacyjne jest najsłabszym ze znanych oddziaływań występujących w przyrodzie.
Można zauważyć, że w zasadzie wzór (3.164) wyznacza nowe wielkości fizyczne
zwane ”masami grawitacyjnymi” (ciężkimi) punktów materialnych. Odgrywają
74
Dynamika punktu materialnego
one rolę ładunków grawitacyjnych podobną do roli ładunków elektrycznych występujących w prawie Coulomba. Masy te nie muszą mieć cokolwiek wspólnego z
”masami bezwładnymi” ciał, które wprowadza do mechaniki druga zasada dynamiki. Jest jednak faktem doświadczalnym, że masa ciężka i bezwładna są sobie
równe. Przyjęcie, że obie masy ciężka i bezwładna to ta sama wielkość fizyczna
stanowi punkt wyjścia ogólnej teorii względności.
Siła, która na Ziemi powoduje spadek ciał musi być tą samą siłą, która działa
pomiędzy planetami układu słonecznego
mg = G
MZ m
,
RZ2
(3.166)
tutaj MZ i RZ to masa i promień Ziemi. Stąd otrzymujemy, że przyspieszenie
grawitacyjne na Ziemi można opisać następującym wzorem:
g=
GMZ
.
RZ2
(3.167)
Równanie to zostało wykorzystane przez Cavendisha, po tym jak wyznaczył stałą
G, do obliczenia masy Ziemi. Jej promień wyznaczono wcześniej po podróży Ferdynanda Magellana dookoła Ziemi. Wartość stałej g na Ziemi różni się nieco w
zależności od szerokości geograficznej; Ziemia nie jest perfekcyjną i doskonale
jednorodną kulą. Znacznie jednak większy wpływ na mierzone różne wartości
przyspieszenia g ma ruch obrotowy Ziemi (w nieinercjalnym układzie odniesienia
pojawia się siła odśrodkowa bezwładności zależna od odległości od osi obrotu
przeciwdziałająca sile grawitacji).
Do opisu siły grawitacji działającej na powierzchni Ziemi możemy używać
→
−
−
wyrażenia F = m→
g . Do obliczeń jednak siły grawitacji w pewnej odległości od
Ziemi (kiedy przybliżenie r ≈ RZ przestaje obowiązywać) należy użyć wyrażenia
(3.164).
Opis pola grawitacyjnego
Większość sił, z którymi mamy do czynienia na co dzień oddziałują przy wzajemnym kontakcie ciał. Jednak siła grawitacji działa na odległość; siła występuję
także wtedy, gdy nie ma kontaktu pomiędzy ciałami. Oddziaływanie to odbywa się
poprzez pole siłowe. Zgodnie z tą ideą pole grawitacyjne otacza każde ciało, które
posiada masę. Inne ciało, które znajdzie się w obszarze działania tego pola doznaje
działania siły grawitacji. Pole grawitacyjne jest więc obiektem fizycznym; istnieje
jako nieustanna gotowość do wywarcia siły. W polu grawitacyjnym zawarta jest
też energia. Obie te cechy pola opisuje się za pomocą dwóch wielkości fizycznych
3.11 Newtonowskie prawo ciążenia powszechnego
75
tj. wektora natężenia pola i wielkości skalarnej - potencjału pola. Zdefiniujemy
teraz obie te wielkości.
Wektor natężenia pola grawitacyjnego wokół masy M to z definicji:
→
−
−
F
GM →
r
→
−
E =
=− 2
.
(3.168)
m
r r
Za pomocą wzoru (3.168) przypisujemy więc każdemu punktowi pola grawitacyjnego wielkość wektorową, która ma związek z działającą siła, ale nie zależy już
od masy m ciała, które w tym polu się znajduje - zależy tylko od masy źródła
pola.
W małym obszarze przestrzennym tuż przy powierzchni Ziemi (dla odległości
h RZ ) natężenie pola grawitacyjnego z dobrym przybliżeniem przyjmuje stałą
wartość
!
GMZ
GMZ
h
GMZ
GMZ
=
E=
=
1
−
2
+
.
.
.
≈
. (3.169)
(RZ + h)2
RZ2
RZ
RZ2
RZ2 (1 + RhZ )2
Zauważmy, że natężenie pola grawitacyjnego przy powierzchni Ziemi ma sens fizy→
−
−
czny przyspieszenia spadku swobodnego E = →
g . Ziemskie pole grawitacyjne
możemy przyjąć za stałe i jednorodne:
−−−→
→
−
g = const.
(3.170)
Linie sił takiego pola są do siebie równoległe. Z definicji (3.168) wynika także, że
siła działająca w ziemskim polu grawitacyjnym ma postać:
→
−
−
F = m→
g.
(3.171)
Energię potencjalną siły grawitacji opisuje wyrażenie:
Ep = −
GM m
.
r
(3.172)
Wielkość ta nie nadaje się do opisu pola siłowego, ponieważ zależy od masy m
ciała, które znajduje się w polu. Wielkość:
ϕ=
Ep
GM
=−
,
m
r
(3.173)
zwana potencjałem pola grawitacyjnego zależy już tylko od masy M źródła opisuje pole grawitacyjne wokół masy M . Pomiędzy natężeniem, a potencjałem
pola istnieje związek
→
−
→
−
E = − ∇ϕ.
(3.174)
76
Dynamika punktu materialnego
→
−
→
−
Jest to analog wyrażenia F = − ∇Ep . Siły pola grawitacyjnego są zdolne do
wykonania pracy. Praca sił pola przy przesunięciu pomiędzy dwoma punktami
pola r1 i r2 można wyznaczyć jeśli znamy funkcje skalarne ϕ(r1) i ϕ(r2):
W = −m(ϕ(r2) − ϕ(r1)).
(3.175)
Powierzchnie, na których potencjał pola ma jednakową wartość ϕ = const. nazywamy powierzchniami ekwipotencjalnymi. Przy przesunięciu pomiędzy punktami
leżącymi na danej powierzchni ekwipotencjalnej praca sił pola wynosi zero:
→
− →
F · d−
r = 0.
(3.176)
Ze związku (3.176) wynika, że linie sił pola są prostopadłe do powierzchni ekwipotencjalnych.
W małym obszarze przestrzennym tuż przy powierzchni Ziemi (dla odległości
h RZ ) praca jaką wykonują siły pola obliczamy następująco:
W = −(Ep(RZ + h) − Ep(RZ )) = −
GMZ mh
GMZ mh
≈ −mgh.
=− 2
RZ (RZ + h)
RZ (1 + RhZ )
(3.177)
Rozdział 4
Szczególna teoria względności
Przez cały wiek XIX uważano, że wszystkie zjawiska fizyczne powinny dać się w zasadzie sprowadzić do zjawisk mechanicznych. Pogląd ten umocnił się, gdy zjawiska
cieplne, dzięki sukcesom teorii kinetycznej, można było sprowadzić do mechaniki.
Prawa mechaniki jak wiemy są niezmiennicze względem transformacji Galileusza;
zjawiska mechaniczne przebiegają jednakowo we wszystkich inercjalnych układach
odniesienia.
W drugiej połowie XIX wieku dzięki odkryciom Faradaya i pracom Maxwella
ustalono główne prawa rządzące zjawiskami elektrycznymi i magnetycznymi. Z
teorii Maxwella wynika istnienie fal elektromagnetycznych, które rozchodzą się w
próżni we wszystkich kierunkach z tą samą prędkością równą c. Jednak kiedy za
pomocą transformacji Galileusza przetransformujemy ten ruch do innego inercjalnego układu odniesienia poruszającego się względem układu wyjściowego, to
okaże się, że w tym drugim układzie prędkość rozchodzenia się fal będzie zależała
od kierunku. W pewnych kierunkach fale elektromagnetyczne będą rozchodziły
się szybciej, a w innych wolniej. Uważano, że równania Maxwella, a co za tym
idzie, zjawiska elektromagnetyczne wyróżniają pewien układ odniesienia związany
z hipotetycznym ośrodkiem wypełniającym cały wszechświat - eterem. Ośrodek
ten miał być jednocześnie nośnikiem fal elektromagnetycznych. Przypuszczano, że
w układach inercjalnych poruszających się względem eteru równania elektrodynamiki mają postać różną od postaci zaproponowanej przez Maxwella.
Źródła szczególnej teorii względności tkwią w elektromagnetyzmie. Podstawy
pod nią położył przede wszystkim Lorentz. Ważny wkład wniósł też Poincare,
lecz decydujący krok zrobił Einstein. W czasach, gdy Einstein zaczął rozważać
te zagadnienia istniały trzy możliwości: (1) równania Maxwella są niepoprawne,
(2) dla zjawisk elektromagnetyzmu występuje wyróżniony układ odniesienia, (3)
zasadę względności spełniają zarówno prawa mechaniki jak i elektromagnetyzmu,
ale transformację Galileusza, słuszną dla praw mechaniki, trzeba zastąpić innym
rodzajem transformacji. Pierwsza z możliwości po sukcesach doświadczeń Hertza
78
Szczególna teoria względności
była już mało prawdopodobna. Większość fizyków przychylała się do poglądu
wyrażonego w punkcie drugim. Przedstawiano rozmaite wersje elektrodynamiki w
układach ruchomych. Z proponowanych teorii wynikało, że w układach poruszających się względem eteru fale elektrodynamiczne nie powinny rozchodzić się
izotropowo. Przypuszczano, że odpowiednie doświadczenia pozwolą wykryć tą anizotropię - ruch względem eteru. W tym nurcie mieścił się między innymi eksperyment Michelsona - Morleya.
Jeszcze przed opublikowaniem prac Einsteina, Lorentz wykazał, że istnieją takie
przekształcenia zmiennych przestrzennych i czasu, względem których równania
Maxwella są niezmiennicze. Okazało się jednak, że transformacje te zmieniają nie
tylko współrzędne przestrzenne zderzeń fizycznych, ale także przedziały czasu.
Uznano to za ciekawy fakt matematyczny nie wyrażający jednak żadnych treści
fizycznych. Później matematyk i fizyk francuski H. Poincare wysunął pogląd, że dla
wszystkich zjawisk fizycznych musi obowiązywać zasada względności - wszystkie
zjawiska fizyczne powinny przebiegać jednakowo we wszystkich układach inercjalnych. Jednak zasadniczego przełomu dokonał Einstein w pracy z 1905 roku. W
pracy tej wprowadził, nie nawiązując do równań Maxwella, równania transformacji
Lorentza, wychodząc z postulowanej zasady względności obowiązującej dla wszystkich zjawisk fizycznych, oraz zakładając, w nawiązaniu do negatywnego wyniku
doświadczenia Michelsona - Morleya, że szybkość światła w próżni jest taka sama
we wszystkich układach inercjalnych - szybkość światła w próżni jest stałą uniwersalną. Podkreślić tu należy, że Einstein pierwszy odrzucił hipotezę eteru. Uznał,
że istnieje jedynie ruch względny dwóch układów odniesienia, a nie bezwzględna
prędkość względem hipotetycznego eteru. Teoria Einsteina spowodowała modyfikację praw mechaniki dla ruchów z dużymi prędkościami.
4.1
Doświadczenie Michelsona - Morleya
Istotę doświadczenia ilustruje następujący przykład. Dwóch pływaków jednakowo
szybkich ściga się w korycie rzeki (patrz rysunek poniżej). Prędkość nurtu wynosi
v. Obaj ścigają się na dwóch jednakowo długich dystansach 2L. Prędkość każdego
pływaka względem wody wynosi c. Załóżmy, że c v. Jeden z pływaków porusza
się równolegle do brzegów rzeki, od punktu A do B i z powrotem, drugi prostopadle
od punktu A do C i z powrotem do punktu A.
Kiedy pływak na kursie równoległym do brzegów rzeki porusza się zgodnie z
kierunkiem prądu rzeki jego prędkość względem brzegu rzeki wynosi c+v. Czas na
L
przepłynięcie dystansu L (od punktu A do B) wynosi (c+v)
. W drodze powrotnej
4.1 Doświadczenie Michelsona - Morleya
79
pływak musi pokonywać prąd rzeki. Jego prędkość względem brzegu wynosi c − v,
L
a czas na przepłynięcie dystansu od punktu B do A wynosi (c−v)
. Całkowity czas
na pokonanie dystansu 2L przez tego pływaka wynosi:
tk =
2L
L
L
2Lc
2L 1
v2
≈
+
= 2
=
(1
+
).
2
c+v c−v
c − v2
c 1 − vc2
c
c2
(4.1)
Pływak poruszający się prostopadle do brzegów potrzebuje jednakowego czasu na
pokonanie drogi do punktu
C i z powrotem. Prędkość tego pływaka na obu od√
−c walczy z nurtem rzeki,
cinkach drogi wynosi c2 − v 2. Jedna składowa wektora →
druga jest prędkością ruchu w kierunku prostopadłym do brzegów. Całkowity czas
jakiego potrzebuje ten pływak na pokonanie drogi 2L wynosi:
2L
1
2L
r
=
t⊥ = √ 2
c 1−
c − v2
v2
c2
1 v2
2L
≈
(1 + 2 ).
c
2c
(4.2)
Widać więc, że pływak poruszający się w kierunku prostopadłym wygrywa wyścig
(t⊥ < tk ). Różnica czasów obu pływaków:
Lv 2
∆t = tk − t⊥ ≈ 3 .
c
(4.3)
Dokonując więc pomiaru różnic czasu obu pływaków na określonym dystansie
można wyznaczyć prędkość prądu v.
Odpowiednikiem takiego doświadczenia było doświadczenie optyczne Michelsona - Morleya. Rolę pływaków grały dwa promienie świetlne biegnące na jednakowych drogach optycznych w dwóch ramionach interferometru Michelsona.
Jedna z tych dróg była równoległa, a druga prostopadła do kierunku ruchu Ziemi
względem nieruchomego eteru. Spodziewano się zaobserwować wpływ ruchu Ziemi
po orbicie wokół Słońca na czas biegu promieni świetlnych w ramionach interferometru.
80
Szczególna teoria względności
Interferometr Michelsona to zasadniczo układ trzech luster. Płytka L jest lustrem półprzepuszczalnym. Część światła jest przez to lustro przepuszczana w
kierunku L1 , a część zostaje odbita w kierunku L2. Oba lustra L1 i L2 są całkowicie
odbijające. Wiązka światła odbita od L1 dalej po odbiciu od posrebrzanej ścianki
płytki L dochodzi do obserwatora. Światło odbite od L2 po przejściu przez płytkę
L także dociera do lunetki obserwatora. Płytka kompensacyjna K jest konieczna,
aby oba promienie przebiegły jednakową drogę w szkle. Obie wiązki światła odbita
i przepuszczona przez płytkę L są spójne, ponieważ pochodzą z tej samej wiązki
pierwotnej. Fala świetlna w jednej wiązce ma stałą różnicę faz w stosunku do
fali świetlnej w drugiej wiązce. Jeśli te dwie wiązki światła przebywają równe
drogi optyczne to przychodzą w zgodnej fazie i powodują pojawienie się jasnej plamki w wyniku konstruktywnej interferencji. Jeśli droga optyczna jednej z
wiązek wzrasta (np. w wyniku niewielkiego przesunięcia lustra L 1 ), to wiązki przychodzą do lunetki obserwacyjnej coraz bardziej przesunięte w fazie, co powoduje
zmniejszanie się intensywności na skutek destruktywnej interferencji. Jeżeli jedno
zwierciadło zostanie przesunięte o odległość λ4 względem swojego początkowego
położenia, to wiązki będą w przeciwnej fazie i powstanie ciemna plamka. W praktyce wiązka światła ma skończone wymiary wobec czego obserwujemy nie jedną
plamkę a ciąg jasnych ciemnych i prążków. Zmiana położenia któregoś z luster
L1 lub L2 spowoduje przesunięcie się prążków interferencyjnych w polu widzenia
lunetki. Taki sam efekt - ruch prążków interferencyjnych, spowoduje także zmiana
czasu ruchu promienia świetlnego, w którymś z ramion interferometru. Jeśli jedno
z ramion ustawimy na linii północ - południe, a drugie na linii wschód - zachód
tj. w kierunku ruchu orbitalnego Ziemi, to powinno się zaobserwować wpływ tego
ruchu na czas biegu promienia świetlnego. Zakładając, że ruch Ziemi powoduje
zmiany prędkości poruszania się promieni świetlnych w ramionach interferometru
spodziewano się zaobserwować ruch prążków interferencyjnych przy obrocie interferometru o kąt 900.
4.2 Transformacja Lorentza
81
Przyrząd był zamontowany na masywnym bloku pływającym w basenie wypełnionym rtęcią. Promień równoległy powinien dochodzić do pola widzenia lunetki
obserwacyjnej o ∆t później niż prostopadły. Wynik interferencji powinien być taki
jak przy różnicy dróg optycznych.
∆L = c ∆t =
Lv 2
= nλ
c2
(4.4)
Warunkiem powstania jasnego prążka interferencyjnego jest, aby różnica dróg była
całkowitą wielokrotnością użytej długości fali światła λ. Dla światła żółtego oraz
biorąc pod uwagę, że prędkość Ziemi na orbicie wynosi 30 km
, a długość ramion
s
interferometru wynosiła 11m otrzymujemy liczbę długości fal n=0,2. Przy obrocie
interferometru przesunięcie prążków interferencyjnych powinno wynikać z różnicy
dróg optycznych równej 2∆L. Powinno to spowodować przesunięcie prążków o
0,4 rzędu. Dokładność przyrządu pozwalała zaobserwować przesunięcie 40 razy
mniejsze.
W doświadczeniu nie zaobserwowano przesunięcia prążków interferencyjnych.
Wynik doświadczenia Michelsona - Morleya był sprzeczny z przewidywaniami
mechaniki klasycznej.
4.2
Transformacja Lorentza
Szczególna teoria względności oparta jest na dwóch postulatach:
(1) Postulat względności.
Prawa fizyki i wyniki wszystkich doświadczeń przeprowadzonych w ustalonym
układzie odniesienia są takie same we wszystkich inercjalnych układach odniesienia.
(2) Postulat stałej prędkości światła.
Światło rozchodzi się w próżni ze stałą prędkością równą c niezależną od prędkości źródła czy obserwatora.
Postulaty Einsteina powodują modyfikację praw mechaniki dla ruchów z dużymi
prędkościami. Najważniejsza modyfikacja wynika z faktu, że prędkość światła
ma stałą wartość we wszystkich inercjalnych układach odniesienia. Z tego faktu
wynika względność równoczesności - dwa zdarzenia równoczesne w pewnym układzie
nie musza być równoczesne w innych.
82
Szczególna teoria względności
Rozważamy dwa inercjalne układy odniesienia O1 i O2 poruszające się względem
−
siebie z prędkością →
v . Załóżmy, że początki obu układów pokrywały się w chwili
t1 =t2 =0 i tej właśnie chwili umieszczone we wspólnym początku obu układów
źródło światła zostaje włączone. Po pewnym czasie wiązka światła dociera do
punktu M.
Jeśli przyjąć, że prędkość światła ma taką samą wartość dla obu obserwatorów,
to:
r1 = c t 1 ,
r2 = c t 2
(4.5)
Jesteśmy więc zmuszeni przyjąć, że czasy przebiegu t 1 i t2 (mierzone przez obserwatorów O1 i O2 ) są różne. Upływ czasu w obu układach odniesienia jest różny.
Ten fakt jest przyczyną wszystkich efektów, które pojawiają się w kinematyce
relatywistycznej.
Nowa transformacja pomiędzy układami odniesienia powinna zapewniać stałość
prędkości światła. Transformację Galileusza trzeba zastąpić nowym rodzajem transformacji, w której forma kwadratowa x2 + y 2 + z 2 − c2 t2 będzie niezmiennikiem
(wynika to z wyrażonych we współrzędnych kartezjańskich równań (4.5)). Ponadto dla prędkości małych w stosunku dla prędkości światła nowa transformacja
powinna przejść w transformację Galileusza.
Warunki takie spełnia transformacja Lorentza. Wzory transformacji Lorentza
x − βct
x − vt
są następujące:
√
=
= γ(x − βct)
x0 = r
2
v2
1
−
β
1− 2
c
0
y = y
z0 = z
t − β xc
t − cv2 x
x
0
√
t = r
=
=
γ(t
−
β
),
2
v2
c
1
−
β
1 − c2
(4.6)
1
.
(1−β 2 )
gdzie β = vc , γ = √
Transformacja odwrotna ma postać:
x = γ(x0 + βct0 )
y = y0
z = z0
x0
t = γ(t + β )
c
0
(4.7)
4.3 Relatywistyczne składanie prędkości
4.3
83
Relatywistyczne składanie prędkości
Niech układ O’ porusza się względem układu O z prędkością u w kierunku osi x.
W układzie O’ porusza się punkt materialny z prędkością v 0 . Poszukujemy jaka
jest prędkość punktu względem układu O.
Najpierw znajdziemy wyrażenia dla składowych wektora prędkości. Żeby otrzymać odpowiednie wyrażenia relatywistyczne przyjmijmy:
vx0
dx0
= 0
dt
vx =
oraz
dx
.
dt
(4.8)
Korzystając ze wzorów transformacji Lorentza mamy:
β 0
dx ),
c
(4.9)
dx
dx dx0 + βc dt0
vx0 + u
dt0 + βc
vx =
=
=
=
0
uvx0 .
dt
dt0 + βc dx0
1 + βc dx
1
+
dt0
c2
(4.10)
dx = γ(dx0 + βc dt0 ),
dt = γ(dt0 +
gdzie βc = u. Stąd następnie
0
W podobny sposób otrzymać możemy wyrażenia dla pozostałych składowych wek−
tora →
v:
√
√
vy0 1 − β 2
dy
vz0 1 − β 2
dz
vy =
=
,
vz =
=
.
(4.11)
0
uvx0
x
dt
dt
1 + uv
1
+
2
2
c
c
Znajdziemy teraz wartość wektora prędkości dla obserwatora w układzie O.
−
Składowe wektora →
v 0 w układzie O’ to:
vx0 = v 0 cos α,
vy0 = v 0 sin α.
(4.12)
84
Szczególna teoria względności
Stąd możemy zapisać:
v cos α + u
vx =
,
0
1 + uv
cos
α
2
c
0
vy =
r
1−
1+
u2 0
c2 v sin α
uv 0
c2 cos α
(4.13)
q
Wartość prędkości w układzie O wynosi v = vx2 + vy2 , a więc
2 02
−
−
−
−
u +→
v 0 )2 − c12 (→
u2 + v 02 + 2uv 0 cos α − u cv2 sin α (→
u ×→
v 0 )2
=
v =
!
0
2
→
−
→
−0 2
(1 + uv
u
·v
c2 cos α)
1 + c2
2
(4.14)
Ze wzoru (4.14) widać, że relatywistyczna suma dwóch prędkości v 0 = c i u = c
nie może przekroczyć wartości c. Mamy mianowicie:
2c2 + 2c2 cos α − c2 sin2 α
= c2 .
v =
2
(1 + cos α)
2
(4.15)
Zauważmy, że kiedy prędkość u c ( uc ≈ 0) wyrażenie relatywistyczne (4.14)
przechodzi we wzór klasyczny:
→
−
−
−
v 2 = (→
u +→
v 0 )2 .
(4.16)
−
−
−
−
Kiedy wektory prędkości →
u i→
v 0 są równoległe (→
u ×→
v 0 =0) mamy:
−
−
(→
u +→
v 0 )2
v =
! .
0 2
→
−
→
−
1 + u c·2v
2
(4.17)
Wyrażenie (4.17) zapisać można następująco:
u + v0
v=
0 .
1 + uv
2
c
(4.18)
−
−
−
−
Kiedy wektory →
u i→
v 0 są prostopadłe (→
u ·→
v 0 =0), mamy:
1−2 →
1−2 →
−
−
−
−
v 2 = (→
u +→
v 0 )2 − 2 →
u ·−
v 02 = →
u2+→
v 02 − 2 →
u ·−
v 02
c
c
(4.19)
oraz
v 2 = u2 + v 02 −
1 2 02
uv .
c2
(4.20)
4.4 Efekt aberracji gwiezdnej
4.4
85
Efekt aberracji gwiezdnej
Angielski astronom James Brodley żyjący w XVIII wieku zaobserwował, że gwiazdy
wykonują na niebie pozorny ruch kołowy o średnicy kątowej około 41 sekund
i okresie jednego roku. Bradley podał także wyjaśnienie tego zjawiska zwanego
obecnie aberracją gwiezdną - efektem Bradleya. Zjawisko aberracji światła jest
konsekwencją ruchu Ziemi i skończonej prędkości światła. Rozróżnia się aberrację:
dobową (wynikającą z ruchu obrotowego Ziemi), roczną (spowodowaną ruchem
orbitalnym Ziemi) i wiekową (spowodowaną ruchem Układu Słonecznego).
Efekt ten wyjaśnia się następująco. W czasie obserwacji astronomicznej teleskop
wraz z Ziemią znajduję się w ruchu. Światło w czasie tego ruchu pokonuje drogę w
teleskopie od okularu do obiektywu. Aby otrzymać obraz gwiazdy teleskop musi
zostać nachylony pod pewnym kątem θ w stosunku do kierunku prawdziwej pozycji
gwiazdy, tak aby skompensować ruch Ziemi (patrz rysunek poniżej).
Kąt aberracji wynosi zatem:
θ ≈ tg θ =
ut u
= .
ct
c
(4.21)
Dla prędkości ruchu Ziemi po orbicie wokół Słońca równej w przybliżeniu 30 km
s i
8 m
−4
prędkości światła c=3·10 s z wyrażenia (4.21) otrzymujemy θ ≈ 10 rad, czyli
około 20,5 sekundy. Podwojenie tej wartości daje średnicę kątową pozornego ruchu
obrotowego.
Okazuje się, że aberracja gwiezdna jest efektem relatywistycznym. Z transformacji Lorentza wynika mianowicie zmiana kierunku rozchodzenia się światła,
kiedy obserwator lub źródło znajdują się w ruchu.
Według teorii korpuskularnej światło to zbiór fotonów. Niech źródło promieniowa−
nia związane jest z układem O’ poruszającym się z prędkością →
u . Fotony emi−
towane są w tym układzie z prędkością →
v 0 = cnb 0 , gdzie nb 0 jest wersorem propagacji
światła. Obserwator w układzie nieruchomym O obserwuje fotony poruszające się
−
z prędkością →
v = cnb (w obu układach prędkość światła ma tą samą wartość).
86
Szczególna teoria względności
−
−
Pomiędzy składowymi wektorów prędkości →
v i →
v 0 zachodzą zależności opisane
wzorami (4.10) i (4.11). Ze wzorów tych otrzymujemy następujące wzory transformacyjne dla składowych wersorów propagacji światła:
+u
cnx =
,
u
1 + c2 cn0x
cn0x
cny =
cn0y
ny =
n0y
r
1−
1+
u2
c2
,
u
0
cn
2
y
c
cnz =
cn0z
r
1−
1+
u2
c2
,
u
0
cn
2
z
c
(4.22)
a stąd ostatecznie:
n0x + β
,
nx =
1 + βn0x
√
1 − β2
,
1 + βn0x
nz =
n0z
√
1 − β2
,
1 + βn0x
(4.23)
gdzie β = uc .
Przypuśćmy, że układ O’ związany jest z poruszającą się gwiazdą, która wysyła
promieniowanie prostopadle do kierunku ruchu tego układu.
W układzie O’ składowe wersora nb 0 są następujące: n0x = 0, n0y = 1, n0z = 0. Ze
√
wzorów transformacyjnych (4.23) otrzymujemy: nx = β, ny = 1 − β 2 , nz = 0.
W układzie O obserwator widzi więc, że kierunek rozchodzenia się światła ulega
odchyleniu o pewien kąt:
tg θ =
nx
β
.
=√
ny
1 − β2
(4.24)
Nierelatywistyczny wzór na kąt aberracji światła jest więc tylko przybliżeniem
wyrażenia relatywistycznego (4.24). W przypadku, kiedy β = uc jest bardzo małe
wzór (4.24) przechodzi w wyrażenie (4.21).
4.5 Efekt kontrakcji długości
4.5
87
Efekt kontrakcji długości
Według kinematyki relatywistycznej długość liniowa ciała jest największa w układzie,
w którym ciało spoczywa. Ulega skróceniu, w kierunku ruchu, w układzie poruszającym się względem tego układu.
Niech pręt leżący wzdłuż osi x spoczywa w układzie O (nieporuszającym się).
Długość spoczywającego pręta w układzie O wynosi:
l = x2 − x1 .
(4.25)
Pomiaru długości pręta dokonuje także obserwator w układzie poruszającym się z
prędkością v. Długość pręta wyznacza podając w tej samej chwili czasu t 0 położenia
punktów x01 i x02, w których znajdują się końce pręta. Wyznaczona przez niego
długość wynosi l 0
l0 = x02(t0) − x01(t0 ).
(4.26)
Z transformacji Lorentza mamy
x1 = γ(x01 + βct01 ),
x2 = γ(x02 + βct02 ).
(4.27)
Ponieważ pomiar położenia końców pręta w układzie poruszającym się odbywa się
w tej samej chwili czasu, to mamy t01 = t02 . Wobec tego:
l = x2 − x1 = γ(x02 − x01) − γβc(t02 − t01 ) = γ(x02 − x01 ) = γl0,
(4.28)
czyli
q
l0 = l 1 − β 2 .
(4.29)
l0 q
= 1 − β 2 < 1.
l
(4.30)
l0 < l,
(4.31)
Porównajmy obie długości:
Stąd mamy:
a więc mierzona przez obserwatora w układzie O’ długość l 0 jest mniejsza (nastąpiła
kontrakcja długości pręta). Należy tu podkreślić, że skrócenie mierzonej długości
wynika z faktu względności równoczesności - dwa zdarzenia równoczesne w pewnym
układzie odniesienia nie są równoczesne w innym.
88
Szczególna teoria względności
4.6
Efekt dylatacji czasu
Dylatacja czasu to zjawisko polegające na tym, że czas w układzie poruszającym
się płynie wolniej.
Rozważmy dwa zdarzenia A i B, które w układzie O’ dzieli interwał (odcinek)
czasowy ∆t0 = t0B − t0A , przy czym zakładamy, że zdarzenia te zachodzą w tym
samym punkcie przestrzeni x0A = x0B . Oznacza to, że ∆t0 jest odcinkiem czasu
mierzonym przez bezwymiarowy (punktowy) zegar spoczywający w układzie O’.
Układ O’, to układ poruszający się z prędkością v względem układu O. W układzie
O te same dwa zdarzenia A i B wyznaczają przedział czasu ∆t = t B −tA . Ze wzorów
transformacji Lorentza mamy:
β
xA )
c
β
= γ(tB − xA )
c
t0A = γ(tA −
x0A = γ(xA − βctA )
t0B
x0A = γ(xB − βctA )
(4.32)
Stąd
∆t0 = t0B − t0A = γ(tB − tA ) −
γβ
γβ
(xB − xA ) = γ∆t −
(xB − xA ).
c
c
(4.33)
Następnie, ponieważ x0B − x0A = 0 mamy:
xB − x A =
1 0
(xB − x0A ) + βc(tB − tA ) = βc∆t.
γ
(4.34)
Biorąc pod uwagę oba te wyrażenia, otrzymujemy
∆t0 = γ∆t −
γβ
βc∆t = γ(1 − β 2 )∆t,
c
(4.35)
a więc
q
∆t0 = 1 − β 2∆t.
(4.36)
Porównajmy oba przedziały czasu
∆t0 q
= 1 − β 2 < 1.
∆t
(4.37)
∆t0 < ∆t,
(4.38)
Stąd mamy
a więc w układzie poruszającym się czas płynie wolniej (odcinek czasowy w układzie
poruszającym się jest krótszy).
4.7 Relatywistyczny efekt Dopplera
4.7
89
Relatywistyczny efekt Dopplera
Zjawisko Dopplera polega na powstawaniu różnicy pomiędzy długością fal wysyłanych
przez źródło, a rejestrowanych przez obserwatora w przypadkach, gdy albo źródło
fal znajduje się w ruchu albo obserwator zbliża się lub oddala względem nieruchomego źródła. Efekt Dopplera dotyczy wszystkich rodzajów fal. Dla fal dźwiękowych
efekt zależy jednak od prędkości obserwatora oraz źródła względem ośrodka, w
którym te fale się rozchodzą. W akustyce obowiązują cztery wyrażenia opisujące
efekt Dopplera - dwa odnoszące się do przypadku ruchu źródła względem nieruchomego obserwatora, oraz dwa dalsze obowiązujące w przypadku, gdy źródło jest
nieruchome a obserwator jest w ruchu. W przypadku fal elektromagnetycznych
znaczenie ma jedynie prędkość źródła względem obserwatora.
Klasyczne wyjaśnienie efektu Dopplera nie bierze pod uwagę relatywistycznego
zjawiska dylatacji czasu. Wyrażenia klasyczne obowiązują tylko dla małych prędkości źródła względem obserwatora.
Efekt Dopplera jest konsekwencją teorii względności i tylko na gruncie tej teorii
można dokonać jego poprawnego wyjaśnienia. Światło to fala elektromagnetyczna (pulsujące pole elektromagnetyczne poruszające się z prędkością c), która
składa się z dwóch ściśle ze sobą sprzężonych pól elektrycznego i magnetycznego.
W zjawiskach optycznych dominującą rolę odgrywa pole elektryczne. W optyce
przyjęło się opisywać falę świetlną wektorem natężenia pola elektrycznego. Rozważmy
falę płaską pola elektrycznego:
−→
→
−
→
− i(ωt−→
k−
r ),
E = E 0e
(4.39)
→
−
gdzie k = ωc nb jest wektorem falowym (nb to wektor propagacji fali), E 0 jest amplitudą natężenia pola elektrycznego. Przejdźmy teraz do równania fali w układzie
−
poruszającym się z prędkością →
v:
− 0→
0
−
→
−0 →
− 0 i(ω0 t0 −→
k
r
)
E = E 0e
.
(4.40)
→
−−
Faza fali tj. wyrażenie ωt − k →
r jest skalarem, musi więc być niezmiennikiem
transformacji Lorentza:
nb →
nb 0 →
0 0
−
ω(t − r ) = ω (t − −
r 0 ).
c
c
(4.41)
Korzystając z transformacji Lorentza mamy:
"
#
"
#
1
β
1
ω t − (nx x + ny y + nz z) = ω 0 γ(t − x) − (nx γ(x − βct) + n0y y 0 + n0z z 0 ) .
c
c
c
(4.42)
90
Szczególna teoria względności
Równość ta musi być spełniona dla dowolnych wartości zmiennych niezależnych x,
y, z i t. Można ją spełnić tylko wtedy, gdy wyrazy stojące przy zmiennych niezależnych po obu stronach równania (4.42) będą sobie równe. Porównanie wyrazów
stojących przy zmiennej t prowadzi do równania:
ω = ω 0 γ(1 + βn0x ).
(4.43)
Równanie to opisuje relatywistyczny efekt Dopplera. Porównanie wyrazów stojących przy pozostałych zmiennych x, y i z prowadzi do wzorów transformacyjnych
dla składowych wersora propagacji światła opisujących efekt aberracji światła.
Poprzednio wzory te otrzymaliśmy w ramach korpuskularnej teorii światła.
Z równania (4.43) wynika, że w fizyce relatywistycznej mamy do czynienia z
dwoma efektami Dopplera - podłużnym, gdy n0x = ±1 i poprzecznym gdy n0x = 0.
Okazuje się, że efekt Dopplera obserwuje się nie tylko w kierunku rozchodzenia się
fali. W kierunku prostopadłym do kierunku propagacji fali mamy:
ω = γω 0.
(4.44)
Poprzeczny efekt Dopplera jest zjawiskiem czysto relatywistycznym. Dla małych
prędkości v c (β ≈ 0) mamy ω = ω 0 - efekt poprzeczny znika.
W przypadku podłużnego efektu Dopplera (n0x = ±1) mamy do czynienia z falą
biegnąca wzdłuż osi x0 :
√
1+β
ω = ω 0 γ(1 + β) = ω 0 √
.
(4.45)
1−β
Biorąc pod uwagę, że n0x = 1 należy przyjąć β = vc dla układów oddalających się i
β = − vc dla układów zbliżających się. Wzór (4.45) pokazuje, że następuje zmiana
częstości w układzie spoczywającym. W układzie poruszającym się z prędkością v
częstość własna źródła wynosi ω 0 . Obserwator w układzie nieruchomym rejestruje
częstość ω opisaną wzorem (4.45).
√
√
Dla niedużych prędkości v c wyrazy ( 1 + β) i ( 1 − β)−1 można rozwinąć
w szeregi Taylora. Wtedy:
√
1
1
0 1+β
ω=ω√
= ω 0 (1 + β + . . .) · (1 + β + . . .) ≈ ω 0 (1 + β),
(4.46)
1−β
2
2
gdzie ograniczyliśmy się do wyrazów liniowych ze względu na β. Otrzymaliśmy
wyrażenie:
ω = ω 0 (1 + β),
(4.47)
które w przedrelatywistycznej fizyce opisywało efekt Dopplera. Efekt Dopplera jest
konsekwencją teorii względności. Wzór klasyczny (4.47) jest tylko przybliżeniem,
obowiązującym dla małych prędkości, dokładnego relatywistycznego wyrażenia
(4.45).
4.8 Diagramy Minkowskiego
4.8
91
Diagramy Minkowskiego
Szczególna teoria względności wprowadza nowy typ przestrzeni - czasoprzestrzeń i
nową nieeuklidesową geometrię. Czasoprzestrzeń określają trzy współrzędne przestrzenne oraz jedna czasowa. Punkt czasoprzestrzeni (x, y, z, t) nazywa się zdarzeniem. Zjawiska fizyczne w czasoprzestrzeni obrazowo przedstawić można w dwuwymiarowym układzie współrzędnych x, t, który jest płaskim przekrojem czterowymiarowej przestrzeni. Współrzędna x określa położenie, miejsce zdarzenia, natomiast
współrzędna t - czas, w którym to zdarzenie nastąpiło. Oznaczmy współrzędne
czasoprzestrzeni następująco: x0 = ct, x1 = x, x2 = y, x3 = z.
Na diagramach Minkowskiego, przedstawiających zależność pomiędzy x 0 i x1,
wszystkie ciała są w ciągłym ruchu. Ruch ten jest jednak nie tylko przemieszczeniem w przestrzeni, lecz przemieszczeniem w czasie i w przestrzeni. Cząstka materialna poruszając się zmienia swoje współrzędne przestrzenne oraz współrzędną czasową. Cząstka materialna będąca w spoczynku zmienia tylko swoją współrzędną
czasową. Wobec tego punkt reprezentujący cząstkę materialną na diagramie
Minkowskiego będzie kreślił pewną linię - linię świata cząstki.
Prosta A to linia świata cząstki nieruchomej, prosta B, to linia świata cząstki
poruszającej się ze stałą prędkością taką, że tg ϕ = ctx = vc . Linia C to linia świata
cząstki poruszającej się ruchem zmiennym. Zauważmy, że ponieważ prędkość v dla
cząstki materialnej nie może przekroczyć wartości c, to kąt ϕ musi być mniejszy
niż π4 (tg ϕ < 1).
Dla zdarzeń w mechanice klasycznej cała przestrzeń Minkowskiego jest dostępna.
Zbiór punktów na osi x1 , reprezentuje zbiór zdarzeń zachodzących teraz w dowolnej odległości od obserwatora, znajdującego się w punkcie O. Półpłaszczyzna górna
reprezentuje zdarzenia, które dopiero zajdą (w różnych odległościach od obserwatora) w przyszłości. Półpłaszczyzna pod osią x1 przedstawia zdarzenie, które już
zaszły czyli należą do przeszłości.
92
Szczególna teoria względności
Czasoprzestrzeń fizyki klasycznej
Czasoprzestrzeń fizyki relatywistycznej
W czasoprzestrzeni fizyki relatywistycznej istnieje taka jej część, która nie jest
osiągalna dla zdarzeń. Cząstki materialne, będące w spoczynku lub poruszające
się, w przestrzeni Minkowskiego kreślą krzywe zwane liniami świata. Linia świata
dowolnej cząstki nie może wyjść poza stożek świetlny - obszar wyznaczony przez
linie świata fotonu. Istnieją więc punkty w czasoprzestrzeni, które są nieosiągalne.
Istnienie niedostępnej części przestrzeni Minkowskiego jest jednocześnie ograniczeniem dla zasady przyczynowości: cząstki mają oddziaływać tylko wtedy, gdy znajduję się we wspólnej części swych stożków świetlnych. Teraźniejszość na diagramie
to punkt w początku układu współrzędnych. Stożek świetlny oddziela wszystkie
zdarzenia w przeszłości i przyszłości, które można połączyć jakimkolwiek oddziaływaniem z danym zdarzeniem zachodzącym w teraźniejszości od tych, z którymi
nie ma związku przyczynowo-skutkowego.
4.8 Diagramy Minkowskiego
93
Transformacja Lorentza1 w dwuwymiarowym układzie współrzędnych x0, x1
zespala współrzędną przestrzenną i współrzędną czasową następująco:
x00 = γ(x0 − βx1)
x01 = γ(x1 − βx0)
(4.49)
Jeśli podstawimy2
γ = cosh ψ
βγ = sinh ψ,
(4.50)
to wtedy wzory transformacji Lorentza:
x00 = x0 cosh ψ − x1 sinh ψ
x01 = −x0 sinh ψ + x1 cosh ψ,
(4.51)
graficznie przedstawić można jako obroty osi x0 i x1 o kąt rzeczywisty ψ taki, że
tgh ψ = β = vc .
1
2
Wzory transformacji Lorentza:
x − vt
x − βct
q
=p
= γ(x − βct)
v2
1 − β2
1 − c2
x0
=
y0
= y
z0
= z
t0
=
t − v2 x
t − β xc
x
q c
=p
= γ(t − β ),
2
c
1 − β2
1 − vc2
(4.48)
Funkcje hiperboliczne są analogami funkcji trygonometrycznych, w tym sensie, że tak jak okrąg parame-
tryzuje się funkcjami trygonometrycznymi (jeśli wykreślamy krzywą, która jest miejscem geometrycznym punktów o
współrzędnych x = sin t i y = cos t dla parametru t z przedziału 0÷2π, to otrzymamy okrąg), tak hiperbolę parametryzuje się funkcjami hiperbolicznymi. Wszystkie wzory (tożsamości) trygonometryczne mają swoje odpowiedniki
hiperboliczne. Dla funkcji trygonometrycznych mamy:
eiϕ − e−iϕ
sin ϕ =
,
2i
cos ϕ =
eiϕ + e−iϕ
2
sin2 ϕ + cos2 ϕ = 1.
oraz
Dla funkcji hiperbolicznych:
sinh ψ =
oraz
eψ − e−ψ
,
2
cosh ψ =
cosh2 ψ − sinh2 ψ = 1.
eψ + e−ψ
2
94
Szczególna teoria względności
Kąt obrotu ψ nie może przekroczyć wartości π4 (tg ψ ¬ 1). Transformacja (4.51)
02
pozostawia niezmieniony interwał czasoprzestrzenny x 02
1 − x0 :
2
2
2
2
02
2
2
2
2
x02
1 − x0 = x1 (cosh ψ − sinh ψ) − x0 (cosh ψ − sinh ψ) = x1 − x0 .
(4.52)
W układzie współrzędnych x0, x1 równanie x21 −x20 = const. przedstawia hiperbolę,
dla której linie świata fotonu są asymptotami.
4.9
Efekty relatywistyczne na diagramach Minkowskiego
Czasoprzestrzeń przedstawiona na dwuwymiarowej płaszczyźnie ulega deformacji. Dla oceny długości odcinków na diagramach Minkowskiego należy stosować
skalowanie przy użyciu hiperbol odmierzających jednostki czasu i długości. Hiperbole skalujące o równaniach x21 − x20 = 1 i x21 − x20 = −1 wyznaczają jednostki
miary na osiach x0 i x1. Hiperbole te są miejscami geometrycznymi punktów jednakowo odległych od początku układów współrzędnych (pełnią one taką role jaką
w geometrii euklidesowej pełnią równania okręgu).
Hiperbola o równaniu x21 − x20 = −1 odmierza na osi czasu x0 jednostkę miary.
Dla x1 = 0 mamy x20 = 1 czyli x0 = ±1. Podobnie hiperbola x21 − x20 = 1 odmierza
4.9 Efekty relatywistyczne na diagramach Minkowskiego
95
na osi x1 jednostkę miary, ponieważ dla x0 = 0 mamy x21 = 1 czyli x1 = ±1.
Równoczesność zdarzeń
Zdarzenia A i B równoczesne w układzie nieruchomym nie są równoczesne dla
obserwatora w układzie poruszającym się.
Zdarzenia równoczesne w układzie nieruchomym leżą na prostej równoległej do
osi x1, a w układzie poruszającym się leżą na prostej równoległej do osi x 01 .
Kontrakcja długości
Pręt o długości l spoczywa w układzie nieruchomym. Ponieważ pręt spoczywa w
układzie O linie świata końców pręta są prostymi równoległymi do osi x 0. Obserwator znajdujący się w układzie poruszającym się w tej samej chwili czasu dokonuje
pomiaru położenia początku i końca pręta. W układzie poruszającym się linia
zdarzeń równoczesnych jest równoległa do osi x01. Obserwator w układzie poruszającym się wyznacza wiec długość l 0 . Hiperbola skalująca pokazuje, że mierzona
długość jest mniejsza.
Efekty relatywistyczne są perspektywiczne. Rysunek poniżej przedstawia pręt
o długości l 0 spoczywający w układzie poruszającym się. Obserwator znajduje się
w układzie nieruchomym. Wyznaczona przez niego długość wynosi l. Hiperbola
skalująca pokazuje, że długość l jest mniejsza niż l 0. Niezależnie więc od tego czy
96
Szczególna teoria względności
obserwator znajduje się w układzie poruszającym się czy tez będącym w spoczynku
mierzona przez niego długość jest zawsze mniejsza.
Dylatacja czasu
Zegar umieszczony w układzie poruszającym się odmierza odcinek czasu ∆t 0 . Dla
obserwatora w układzie nieruchomym linia zdarzeń równoczesnych jest równoległa
do osi x1 . Dla niego więc zdarzenie, które wyznacza koniec pomiaru czasu w
układzie poruszającym się jest równoczesne ze zdarzeniem, które wyznacza koniec
interwału czasowego ∆t na rysunku poniżej. Hiperbola skalująca pokazuje, że
∆t < ∆t0 . W układzie poruszającym się czas płynie więc wolniej.
4.10
Transformacja Lorentza jako obrót układu współrzędnych
Transformację Lorentza można także przedstawić jako zwykły (euklidesowy) obrót
układu współrzędnych, jeśli oś czasu przyjmuje wartości urojone.
Połóżmy ψ = iϕ. Wtedy mamy (patrz przypis na stronie 93):
cosh ψ = cos ϕ
sinh ψ = i sin ϕ
(4.53)
4.10 Transformacja Lorentza jako obrót układu współrzędnych
97
oraz transformacja (4.51) przyjmuje postać:
x00 = x0 cos ϕ − ix1 sin ϕ
x01 = −ix0 sin ϕ + x1 cos ϕ.
(4.54)
Wprowadźmy jeszcze oznaczenie x4 = ix0 = ict. Wtedy transformację Lorentza
przedstawić można jako obrót o kąt ϕ dwuwymiarowego układów współrzędnych
x1, x4 na płaszczyźnie.
x01 = x1 cos ϕ − x4 sin ϕ
x04 = x1 sin ϕ + x4 cos ϕ.
(4.55)
Zauważmy jednak, że kąt obrotu jest urojony tg ϕ = −iβ, (cos ϕ = γ, sin ϕ =
−iβγ). Mamy tu też do czynienia z deformacją, która wynika z faktu, że cos ϕ > 1.
Efekty mechaniki relatywistycznej można także zilustrować w układzie współrzędnych x1,x4.
Składanie prędkości
Posługując się interpretacją geometryczną transformacji Lorentza wyprowadzić
można wzory na relatywistyczne składanie prędkości. Składanie prędkości równoległych ma prostą interpretację geometryczną - dodawanie prędkości jest dodawaniem
obrotów na płaszczyźnie ϕ=ϕ1 + ϕ2 :
tg ϕ1 + tg ϕ2
tg ϕ = tg(ϕ1 + ϕ2) =
.
(4.56)
1 − tg ϕ1 tg ϕ2
Ponieważ tangens kąta obrotu związany jest z prędkością wzorem tg ϕ = −iβ
mamy:
β1 + β 2
β=
,
(4.57)
1 + β 1 β2
oraz
v1 + v2
v=
.
(4.58)
1 + v1c2v2
Otrzymaliśmy więc wzór na składanie prędkości równoległych. Aby otrzymać wzór
na kwadrat prędkości wypadkowej należałoby składać obroty w przestrzeni, a nie
na płaszczyźnie.
98
Szczególna teoria względności
Równoczesność zdarzeń
Zdarzenia A i B równoczesne w układzie nieruchomym nie są równoczesne dla
obserwatora w układzie poruszającym się.
Efekt kontrakcji długości
Niech pręt spoczywa w układzie nieruchomym. Obserwator w chwili t 0 = 0 w
układzie poruszającym się dokonuje pomiaru położenia początku i końca pręta.
Z zależności dla trójkąta prostokątnego o bokach l, l 0 mamy:
Widzimy więc, że
l
1
= cos ϕ = √
> 1.
0
l
1 − β2
(4.59)
l > l0.
(4.60)
Mierzona przez obserwatora w układzie poruszającym się długość jest mniejsza:
q
l0 = l 1 − β 2 .
(4.61)
4.11 Relatywistyczny pęd i moment pędu
99
Dylatacja czasu
Niech zegar znajdujący się w układzie poruszającym się odmierza odcinek czasu
∆t0 . Pomiar upływu czasu dokonany przez obserwatora w układzie nieruchomym
wynosi ∆t.
Z rysunku wynika, że:
Widzimy więc, że
∆t
1
√
=
cos
ϕ
=
> 1.
∆t0
1 − β2
(4.62)
∆t > ∆t0 ,
(4.63)
interwał czasowy dla obserwatora w układzie poruszającym się jest krótszy - czas
płynie wolniej. Jednocześnie mamy:
q
∆t0 = ∆t 1 − β 2.
4.11
(4.64)
Relatywistyczny pęd i moment pędu
Szczególna teoria względności wprowadza nowe relatywistyczne definicje wielkości
dynamicznych takich jak pęd, moment pędu i energii. Te nowe definicje muszą
mieć taką postać, aby dla małych prędkości przechodziły w wyrażenia klasyczne
(zasada korespondencji) i aby zapewniały one spełnienie, wynikających z symetrii
przestrzeni i czasu, zasad zachowania pędu, moment pędu i energii. Zasady zachowania obowiązują dla wszystkich znanych obecnie rodzajów oddziaływań. Zasady zachowania mają charakter ogólniejszy niż prawa fizyki. Jak już wspomniano
w rozdziale 3.8 według twierdzenia Noether każdemu rodzajowi symetrii w przyrodzie odpowiada określona zasada zachowania.
100
Szczególna teoria względności
Pęd relatywistyczny
−
W mechanice klasycznej pęd →
p , to iloczyn masy i prędkości ciała:
→
−
−
p = m→
v.
(4.65)
Pokażemy, że w mechanice relatywistycznej definicję (4.65) należy zastąpić następującym wyrażeniem:
−
m0 →
v
→
−
−
r
p =
= γ m0 →
v,
(4.66)
2
1 − vc2
gdzie m0 to masa spoczynkowa cząstki (masa cząstki spoczywającej w danym
układzie inercjalnym). Dla małych prędkości (β ≈ 0), wyrażenie relatywistyczne
przechodzi w klasyczne (4.65).
Rozważmy zderzenia sprężyste dwóch jednakowych kul A i B w poruszającym
−
się z prędkością →
v układzie odniesienia O’. Niech w układzie O’ kule mają prędkości odpowiednio równe:
→
−
v 0A = V xb 0 ,
→
−
v 0B = −V xb 0 .
(4.67)
Prędkości kul A i B mierzone przez obserwatora w układzie nieruchomym O są
następujące:
vA =
V +v
,
1 + vV
c2
vB = −
V +v
.
1 − vV
c2
(4.68)
Zastosujemy dla chwili zderzenia prawo zachowania pędu:
→
−
−
−
pA+→
pB =→
p w,
(4.69)
−
−
−
gdzie →
pA i →
p B to pędy kul przed zderzeniem, a →
p w to wypadkowy pęd układu
ciał w chwili zderzenia.
W układzie O’ w chwili zderzenia obie kule są w spoczynku:
m0 V − m0 V = 0,
(4.70)
4.11 Relatywistyczny pęd i moment pędu
101
gdzie m0 to masa każdej z kul. Podczas, gdy obserwator w O’ układzie widzi masy
chwilowo w spoczynku, obserwator w układzie O widzi, że w chwili zderzenia
poruszają się one z prędkością v.
mA vA − mB vB = (mA + mB )v.
(4.71)
Zasada zachowania pędu powinna być spełniona w obu układach. Przewidując
komplikacje jakie mogą wystąpić, ze spełnieniem tej zasady w układzie O po zastosowaniu wzorów transformacyjnych (4.68) dla prędkości obu kul przypisaliśmy
masom kul symbole mA i mB . Po zastosowaniu wzorów transformacyjnych (4.68)
z, wyrażenia (4.71) mamy:
mA
a następnie:
V +v
−V + v
= (mA + mB )v,
V v + mB
1 + c2
1 − Vc2v
(4.72)
mA V
mB V
−
= 0.
1 + Vc2v 1 − Vc2v
(4.73)
Widać więc, że gdyby przyjąć, że dla obserwatora w układzie nieruchomym m A =m0
i mB =m0 wyrażenie (4.73) nie przejdzie w (4.70). Musimy więc przyjąć, że masy
kul A i B w układzie O muszą się zmienić. Połóżmy:
m0
m0
r
,
m
=
.
(4.74)
mA = r
B
2
2
vA
vB
1 − c2
1 − c2
Po zastosowaniu wzorów (4.68) na prędkości vA i vB kul w układzie nieruchomym
O mamy:
mA =
v
u
u
t
m0 (1 +
1+
Vv
c2
!2
−
Vv
)
c2
V
c
+
v
c
mB =
!2 ,
v
u
u
t
m0 (1 −
1−
Vv
c2
!2
Vv
)
c2
− −
V
c
+
v
c
!2 .
(4.75)
Po wykonaniu prostych obliczeń można pokazać, że mianowniki w obu wyrażeniach
powyżej są takie same. Wyrażenia na mA i mB podstawiamy teraz do równań
(4.73). Otrzymujemy:
m0 1 +
1+
Vv
c2
Vv
c2
!
V
−
m0 1 −
1−
Vv
c2
Vv
c2
!
V
= 0,
(4.76)
W otrzymanym równaniu (4.76) opuszczono takie same czynniki występujące w
mianownikach obu wyrazów różnicy. Z równania (4.76) mamy:
m0 V − m0 V = 0.
(4.77)
102
Szczególna teoria względności
Zasada zachowania pędu ma teraz w obu układach taką samą postać.
Aby zasada zachowania pędu była spełniona w mechanice relatywistycznej
musimy przyjąć, że masa zależy od układu odniesienia:
m(0)
m(v) = r
.
(4.78)
v2
1 − c2
W układzie odniesienia, w którym masa spoczywa m(0)=m0. W układzie odniesienia
względem, którego masa jest w ruchu z prędkością v masa rośnie zgodnie ze wzorem
(4.78). Kiedy prędkość zbliża się do c masa ciała dąży do nieskończoności.
Masa jest jednak wielkością skalarną i nie powinna podlegać zmianom przy
transformacji współrzędnych. Część autorów woli więc traktować obserwowany w
doświadczeniach wzrost masy szybkich cząstek jako wzrost pędu:
−
m0 →
v
→
−
p =r
,
(4.79)
v2
1 − c2
którego przyczyną jest różnica pomiędzy czasem własnym cząstki, a czasem laboratoryjnym.
Relatywistyczny moment pędu
Moment pędu to wielkość wektorowa zdefiniowana następująco:
→
−
−
−
L =→
r ×→
p.
(4.80)
W mechanice relatywistycznej definicję (4.80) należy zastąpić następującym wyrażeniem:
→
−
−
r × m0 →
v
→
−
−
−
L = r
= γm0→
r ×→
v.
(4.81)
v2
1 − c2
−
−
−
r ×→
v to z definicji wektor prędkości polowej →
σ . Stąd w mechanice
Iloczyn 1 →
2
relatywistycznej:
−
2m0 →
σ
→
−
−
r
L =
= 2γm0→
σ.
2
1 − vc2
(4.82)
4.12 Relatywistyczna energia kinetyczna
103
r
2
Zauważymy jednak, że ze względu na zależny od prędkości czynnik 1 − vc2 w
mechanice relatywistycznej ze stałości momentu pędu nie wynika stałość prędkości
polowej.
4.12
Relatywistyczna energia kinetyczna
W mechanice klasycznej przy wyprowadzeniu wzoru na energię kinetyczną wyszliśmy z drugiego prawa ruchu (uogólniona postać drugiego prawa ruchu obowiązuje także w mechanice relatywistycznej):
−
d→
p
→
−
F =
.
(4.83)
dt
Następnie obie strony równania (4.83) pomnożyliśmy skalarnie przez infinitezy−
malny wektor przesunięcia d→
r:
−
d→
p
→
− →
−
−
· d→
r.
(4.84)
F ·dr =
dt
→
−
→
− −
−
Lewa strona tego wyrażenia to praca siły F przy przesunięciu d→
r , (dW = F ·d→
r ),
prawa strona wyrażenia przedstawia zmianę energii kinetycznej dE k :
−
−
−
−
dEk = d→
p ·→
v =→
v · d(m→
v ) = v d(mv).
(4.85)
W mechanice relatywistycznej m=m(v), zatem przekształcając dalej wyrażenie
(4.85) mamy:
dEk = v 2 dm + mv dv.
(4.86)
Weźmy teraz pod uwagę wzór na relatywistyczną zależność masy od prędkości:
m0
m=r
,
(4.87)
v2
1 − c2
a stąd
v2
m (1 − 2 ) = m20
c
(4.88)
m2 c2 = m20 c2 + m2 v 2.
(4.89)
2
oraz
Zróżniczkujemy teraz obie strony wyrażenia (4.89) pamiętając przy tym, że m 0 i
c to stałe. Mamy wtedy:
2mc2 dm = 2mv 2dm + 2m2 v dv
(4.90)
104
Szczególna teoria względności
oraz
c2 dm = v 2 dm + mv dv.
(4.91)
Prawe strony wyrażeń (4.91) i (4.86) są takie same. Stąd
dEk = c2 dm.
(4.92)
Wzór ten pokazuje, że w mechanice relatywistycznej zmiana energii kinetycznej
związania jest ze zmianą masy. Scałkujemy obie strony wyrażenia (4.92):
Z E
k
0
dEk = c
2
Z m
m0
dm.
(4.93)
Otrzymujemy:
Ek = c2 (m − m0 ).
(4.94)
Iloczyn m0 c2 to energia spoczynkowa cząstki, a iloczyn mc2 to energia całkowita:
E = mc2 .
(4.95)
Ten słynny wzór Einsteina pokazuje, że energia i masa to dwie miary tej samej
wielkości fizycznej - stały czynnik c2 pochodzi od wyboru jednostek, w których
mierzymy masę i energię. W fizyce relatywistycznej zamiast zasad zachowania
masy i energii mamy zasadę zachowania masy - energii. Z wyrażenia (4.94) wynika,
że energia całkowita:
E = m 0 c2 + E k .
(4.96)
W równaniu tym energię spoczynkową m0 c2 interpretujemy jako energię potencjalną cząstki. Rozumiemy przez to, że np. przy rozpadzie cząstki wielkość ta może
się zamieniać częściowo na energię spoczynkową nowo powstałych cząstek, częściowo zaś na inne formy energii, w tym także na energię kinetyczną tych cząstek.
Powróćmy do rozważań nad relatywistyczną energią kinetyczną. Wyrażenie relatywistyczne
Ek = (m − m0 )c2 ,
(4.97)
dla małych prędkości przechodzi we wzór klasyczny. Rozwijając w szereg Taylora
wyrażenie na γ mamy:
γ=
r
1
1−
v2
c2
1 v2
≈ 1 + 2 + ...,
2c
(4.98)
4.12 Relatywistyczna energia kinetyczna
105
a stąd dalej
Ek = (m − m0 )c2 = m0 c2 (γ − 1) ≈ m0 c2
1 v2
1
=
m0 v 2 .
2
2c
2
(4.99)
Na zakończenie zauważmy, że klasyczne wyrażenie:
1
Ek = mv 2 ,
2
(4.100)
po użyciu relatywistycznego wzoru na zależność masy od prędkości, nie przechodzi
w prawidłowe wyrażenie na relatywistyczną energię kinetyczną.
Związek pomiędzy pędem relatywistycznym i energią
Pęd relatywistyczny to iloczyn masy i prędkości:
→
−
−
p = m→
v,
(4.101)
gdzie m = m(v):
m=
r
m0
1−
v2
c2
.
(4.102)
Biorąc pod uwagę relatywistyczną równoważność masy i energii (E = mc 2 ) z
definicji (4.101) mamy:
E−
→
−
p = 2→
v.
c
(4.103)
Jest to równanie wektorowe wskazujące na zależność pomiędzy pędem i energią
całkowitą cząstki. Możemy także poszukać zależności skalarnej. Z równania (4.102)
otrzymujemy
m2 c2 = m2 v 2 + m20 c2 .
(4.104)
Następnie obie strony tego wyrażenia mnożymy przez c2 :
m2 c4 = m2 v 2c2 + m20 c4
(4.105)
E 2 = p2 c2 + m20 c4 ,
(4.106)
i otrzymujemy
lub
q
E = c p2 + (m0 c)2.
(4.107)
106
Szczególna teoria względności
Z wyrażenia (4.106) możemy także otrzymać wzór na pęd relatywistyczny
1q 2
p=
E − (m0 c2 )2.
(4.108)
c
Uzyskaliśmy wyrażenia, z których często korzysta się w fizyce jądrowej wysokich
energii do obliczania energii całkowitej cząstki, gdy znamy jej pęd lub gdy znana
jest jej energia do obliczeń pędu.
Związki (4.103) i (4.108) pomiędzy pędem relatywistycznym i energią całkowitą
cząstki pozwalają przewidzieć własności cząstki o zerowej masie spoczynkowej. Z
wyrażenia (4.108) wynika, że pęd cząstki o masie spoczynkowej m 0 =0 wynosi:
1
p = E.
c
(4.109)
Podstawiając tą wartość p do wzoru (4.103) mamy:
E
E
= 2 v,
c
c
a stąd obliczając prędkość cząstki otrzymujemy:
v = c.
(4.110)
(4.111)
Oznacza to, ze cząstka o zerowej masie spoczynkowej musi poruszać się z prędkością światła i nigdy nie może spoczywać w układzie inercjalnym. Cząstką taka
jest foton. Przenosi on energię E = hν i związany z tą energią pęd (patrz wzór
(4.109)) p = hν
= hλ z prędkością c.
c
4.13
Efekt Comptona
Wyjaśnienie wyników badań efektu Comptona jest doskonałą ilustracją poprawności
wzorów dynamiki relatywistycznej.
Na początku XX wieku przeprowadzano eksperymenty, które potwierdzały teorię
korpuskularną światła. Jednym z nich było doświadczenie Comptona. Compton
prowadził doświadczenie z rozpraszaniem promieniowania rentgenowskiego na różnych
materiałach. Odkrył, że w rozproszonym promieniowaniu obok promieniowania o
częstotliwości padającej wiązki znajduje się także promieniowanie o nieco niższej
częstotliwości, co wskazuje na częściową utratę energii padającego światła. Schemat
doświadczenia Comptona przedstawia poniższy rysunek.
Doświadczenie prowadzono z różnymi pierwiastkami (zbadano 15 różnych pierwiastków) i zawsze obserwowano takie same przesunięcia częstotliwości w rozpraszanym
promieniowaniu, dla danego kąta obserwacji α, niezależnie od częstotliwości wiązki
4.13 Efekt Comptona
107
padającej. Zaobserwowane przesunięcie wykazywało tylko zależności od kata rozproszenia.
W doświadczeniach z pierwiastkami o dużej liczbie Z należało użyć bardziej wysokoenergetycznego promieniowania. Efektu Comptona nie zaobserwowano jednocześnie
w doświadczeniach z promieniowaniem elektromagnetycznym w zakresie widzialnym. Typowe wyniki doświadczenia Comptona przedstawiają rysunki poniżej.
Zjawisko Comptona można wyjaśnić jako wynik sprężystego zderzenia fotonu z
elektronem. W przypadku pierwiastków, dla których zaobserwowano efekt energie
wiązania elektronów są stosunkowo niewielkie w porównaniu z energią fotonów
twardego promieniowania rentgenowskiego. Elektrony takie można traktować jako
swobodne. Można przyjąć, że przed zderzeniem fotonu energia kinetyczna tych
elektronów jest równa zeru.
Aby wyjaśnić zjawisko zderzenia sprężystego cząstek należy skorzystać z zasad
zachowania pędu i energii. Pęd jest wielkością wektorową - zasada zachowania
108
Szczególna teoria względności
pędu dla składowych x i y ma postać:
hν
hν 0
=
cos α + pe cos β,
c
c
hν 0
sin α = pe sin β,
c
(4.112)
gdzie pe to pęd odrzuconego elektronu. Podnosząc do kwadratu obie strony równania i dodając je stronami otrzymujemy:
hν
c
!2
hν 0
2hνhν 0
−
cos α +
c2
c
!2
= p2e .
(4.113)
Z drugiej strony pęd elektronu związany jest z jego energią całkowitą związkiem:
1q 2
E − (m0c2 )2,
pe =
c
(4.114)
E = E k + m 0 c2 .
(4.115)
gdzie
Ze wzorów (4.114) i (4.115) mamy
p2e
Ek2
= 2 + 2Ek m0 .
c
(4.116)
Z zasady zachowania energii, w zderzeniu fotonu z elektronem, elektron wykazuje
energię kinetyczną równą:
Ek = hν − hν 0 , .
(4.117)
Biorąc pod uwagę wyrażenie (4.117) mamy dalej:
p2e
(hν − hν 0)2
=
+ 2m0(hν − hν 0).
2
c
(4.118)
Możemy teraz porównać oba wyrażenia (4.118) i (4.113) na p 2e . Otrzymujemy:
hν hν 0
m0 (hν − hν ) =
(1 − cos α),
c2
(4.119)
c
c
h
−
=
(1 − cos α),
ν0 ν
m0 c
(4.120)
∆λ = λ0 − λ = Λ(1 − cos α),
(4.121)
0
a stąd
lub
4.13 Efekt Comptona
109
gdzie Λ= mh0 c =0, 024 · 10−10m, to comptonowska długość fali.
Przedstawiona teoria nie wyjaśnia stosunków natężeniowych w rozpraszanym
promieniowaniu. Większa szerokość piku odpowiadająca promieniowaniu wtórnemu
wynika z faktu, że elektrony rozpraszające promieniowanie nie są w spoczynku,
ale wykazują pewien niewielki ruch wokół położenia równowagi (ich energia kinetyczna w momencie zderzenia nie jest dokładnie równa zeru).
Efekt Comptona jest w sprzeczności z teorią falową światła. Według teorii
falowej żadne przesunięcie częstotliwości w rozpraszanym promieniowaniu nie powinno wystąpić. Padająca wiązka światła o częstotliwości ν powinna spowodować
oscylacje elektronu o tej samej częstotliwości. Z kolei drgający elektron powinien
reemitować promieniowanie elektromagnetyczne o częstotliwości zgodnej z częstotliwością drgań.