Obwód nierozgałęziony prądu stałego

1
Obwód nierozgałęziony prądu stałego
1 . I d e a l n e i r z e c z yw i s t e ź r ó d ł a n a p i ę c i a .
O p o r n i k i , g r ze j n i k i , ża r ó wk i s t a wi a j ą p r ze p ł ywo wi p r ą d u e l e k t r yc zn e g o
p e wi e n o p ó r . D o j e g o p o k o n a n i a p o t r ze b n a j e s t s i ł a e l e k t r o m o t o r yc zn a ( S E M )
d o s t a r c zo n a p r ze z źr ó d ł o n a p i ę c i a . W i e l k o ś c i ą c h a r a k t e r yzu j ą c ą k a żd e
źr ó d ł o n a p i ę c i a j e s t j e g o s i ł a e l e k t r o m o t o r yc zn a , c zyl i n a p i ę c i e źr ó d ł a
o zn a c zo n e l i t e r ą E . N a l e ży j e d n a k p a m i ę t a ć , że w źr ó d ł a c h p r ą d u
e l e k t r o m a s zyn o wyc h , wyt wa r za n y p r ze z n i e p r ą d m u s i p r ze p ł ywa ć p r ze z i c h
u zwo j e n i a , a w źr ó d ł a c h p r ą d u e l e k t r o c h e m i c zn yc h p r ze z e l e k t r o l i t . Z a r ó wn o
u zwo j e n i a j a k i e l e k t r o l i t s t a wi a j ą p r ze p ł ywo wi p r ą d u p e wi e n o p ó r zwa n y
o p o r e m w e w n ę t r z n ym a l b o r e z ys t a n c j ą w e w n ę t r z n ą źr ó d ł a , o zn a c za n ą
l i t e r k ą R z d o d a n i e m ws k a źn i k a w , a wi ę c R w . I d e a l n ym źr ó d ł e m n a p i ę c i a
m o żn a b y n a zwa ć t a k i e źr ó d ł o n a p i ę c i a , we wn ą t r z k t ó r e g o n i e wys t ę p u j e
s t r a t a m o c y. I d e a l n e ź r ó d ł o n a p i ę c i a j e s t t o źr ó d ł o n i e m a j ą c e r e zys t a n c j i
we wn ę t r zn e j ( R w = 0 ) . A b y o p i s a ć i d e a l n e źr ó d ł o n a p i ę c i a wys t a r c zy zn a ć j e g o
s i ł ę e l e k t r o m o t o r y c zn ą .
R z e c z yw i s t e ź r ó d ł o n a p i ę c i a j e s t t o źr ó d ł o , d o k t ó r e g o o p i s a n i a
p o t r ze b n e s ą d wi e wi e l k o ś c i : - s i ł a e l e k t r o m o t o r yc z n a ( S E M )
- r e z ys t a n c j a w e w n ę t r z n a
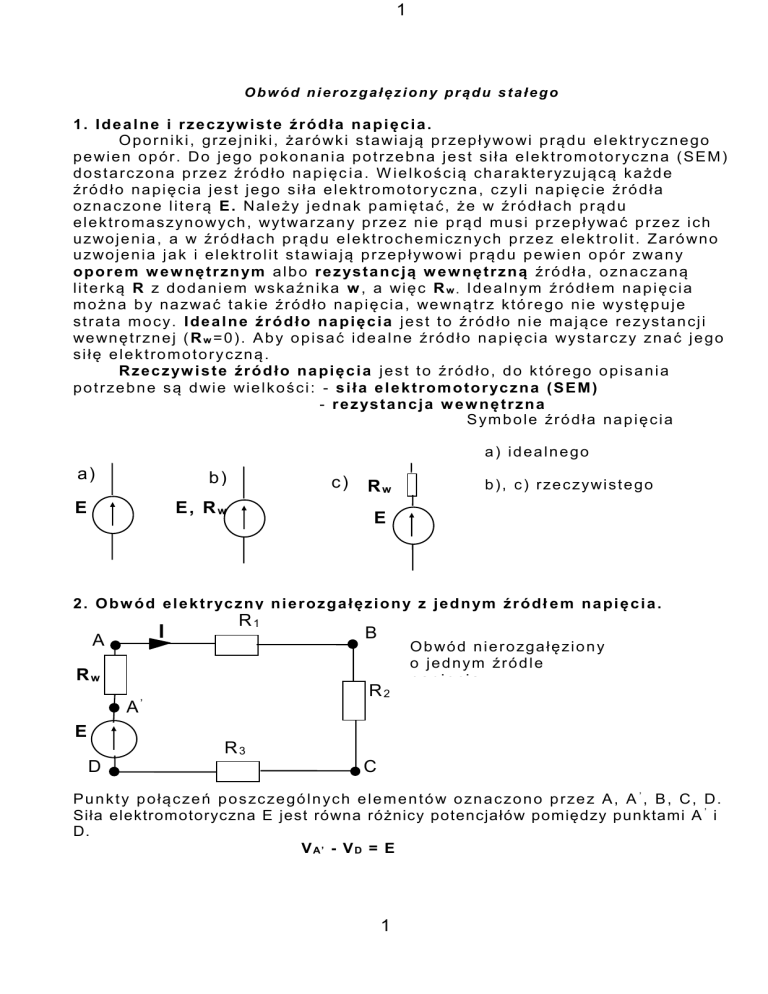
S ym b o l e źr ó d ł a n a p i ę c i a
a) idealnego
a)
b)
E
c)
E, R w
Rw
b ) , c ) r ze c zywi s t e g o
E
2 . O b w ó d e l e k t r yc z n y n i e r o z g a ł ę z i o n y z j e d n ym ź r ó d ł e m n a p i ę c i a .
I
A
R1
B
Rw
A
R2
’
O b wó d n i e r o zg a ł ę zi o n y
o j e d n ym źr ó d l e
napięcia
E
R3
D
C
P u n k t y p o ł ą c ze ń p o s zc ze g ó l n yc h e l e m e n t ó w o zn a c zo n o p r ze z A , A ’ , B , C , D .
Siła elektromotoryczna E jest równa różnicy potencjałów pomiędzy punktami A ’ i
D.
V A’ - V D = E
1
2
W obwodzie płynie prąd zgodnie ze strzałką E. Napięcia na poszczególnych
elementach są równe iloczynowi ich rezystancji i prądu, przy czym wyższy
potencjał jest w punkcie, przez który prąd wchodzi do danego opornika.
W yrazimy napięcie na każdym z oporników jako różnicę potencjałów na jego
końcach, a następnie dodamy do siebie lewe i prawe strony tak otrzymanych
równań.
RW x I = VA’ - VA
R1 x I = VA - VB
R2 x I = Vb - VC
R3 x I = VC - VD
RW x I + R1 x I + R2 x I + R3 x I = VA’ - VD
W yłączając I poza nawias oraz przyjmując V A ’ - V D = E otrzymujemy:
(R W + R 1 + R 2 + R 3 ) x I = E
W obwodzie elektrycznym nierozgałęzionym, zasilanym przez jedno źródło
napięcia, suma napięć na opornikach i na rezystancji wewnętrznej źródła
jesrówna jego sile elektromotorycznej (SEM).
Napięcie na opornikach i na rezystanc ji wewnętrznej źródła nazywamy spadkami
napięć. Dzieląc obustronnie powyższe równanie przez sumę rezystancji
obliczamy prąd w obw odzie .
E
I
RW  R1  R2  R3
Prąd w obw odzie nierozgałęźionym zasilanym przez jedno źródło
napięcia stałego jest równy ilorazowi jego siły elektromotorycznej przez sumę
wszystkich dołączonych rezystancji obwodu łącznie z rezystancją wewnętrzną.
Przykład:
Prądnica elektryczna o sile elektromotorycznej E = 120V i rezystancji
wewnętrznej R W = 1 zasila dwa oporniki o rezyst ancjach R 1 = 5  i R 2 = 9 ,
połączonych w szereg. Obliczyć prąd w obwodzie.
Rozwiązanie:
I
E
120

 8A
RW  R1  R2 1  5  9
3. Obw ód nierozgałęźiony z kilkoma źródłami napięcia
Siła elektromotoryczna niektórych źródeł napięcia, np: elektrochemicznych,
może być niewystarczającą do zasilania pewnych szczególnych odbiorników
energii elektrycznej. W ówczas włączamy w szereg kilka źródeł napięcia tak, aby
ich siły elektromotoryczne były skierowane zgodnie, przyjmuje się za dodatni taki
kierunek obiegu prądu w obwodz ie, który jest zgodny z ruchem wskazuwek
zegara, natomiast taki prosty obwód zamknięty nazywa się „oczkiem” (rys. 1.2a).
Schemat zastępczy takiego obwodu pokazuje rys. 1.2b. Na rys. 1.2a
2
3
przedstawiono trzy źródła napięcia o siłach elektromotorycznych odpow iednio E 1 ,
E 2 , E 3 i rezystancjach wewnętrznych R W 1 , R W 2 , R w3 wraz z dwa opornikami o
rezystancjach R 1 i R 2 .
E2
RW2 E3
RW3
a)
b) E
z
RW!
+
R1
I
-
E1
I
Ez = E1 + E2 + E3
Rz = RW1 + RW2 + RW3 + R1 + R2
R2
rys. 1.2
Rz
Obwód nierozgałęziony z kilkoma źródłami napięcia połączonymi
zgodnie (a) i jego schemat zastępczy (b)
Prąd w obwodzie zależy od sumy wszystkich rezystancji, łącznie z rezystancjami
wewnętrznymi oraz od sumy wszystkich sił elektromotorycznych
działających w tym obwodzie (oczku). Prąd można obliczyć z
zależności:
E1  E2  E3
I
RW 1  RW 2  RW 3  R1  R2
w której w liczniku występuje suma sił elektromotorycznych E z , a w mianowniku
suma wszystkich rezystancji obwodu R z .
Przypuśćmy, że jed no ze źródeł napięcia zostało włączone przeciwnie, tak
że strzałka jego siły elektromotorycznej, np: E 2 , jest skierowana przeciwnie niż
pozostałe (rys. 1.3)
a)
b)
c)
E 2 ;R W 2
E 3 ;R W 3
RW2
RW1
E 1 ;R W 1
E2
E3
RW3
Rz
R1
R1
Ez
E1
R2
R2
rys. 1.3 Obwód nierozgałęziony z kilkoma źródłami napięcia p ołączonymi
niezgodnie (a) i jego schemat rozwinięty (b) oraz zastępczy (c)
3
4
Jeżeli strzałki sił elektromotorycznych w obwodzie są różne, to przy ich
sumowaniu musimy brać jedne ze znakiem +, drugie ze znakiem -. Siłom
elektromotorycznym zgodnym z przyjęty m obiegiem prądu przypisujemy znak +, a
skierowanym przeciwnie znak -. W szystkim rezystencjom wewnętrznym
przypisujemy znak +.
Tak więc w obwodzie na rys. 1.3 a i b prąd
E 1 - E 2 +E 3
I=
Rw1 + Rw2 + Rw3 + R1 + R2
W obw odzie nierozgałęzionym prądu stałego zaw ierającym kilka
źródeł napięcia prąd jest rów ny ilorazow i sumy ich sił elektromotorycznych
z uw zględnieniem znaków i sumy w szystkich rezystencji obw odu.
Prąd płynie zgodnie z kierunkiem przeważających sił elektromotorycznych i
tak logicznie należałoby obierac strzałkę prądu. Nie jest to jednak konieczne,
gdyż przy przeciwnym zwrocie strzałki prądu otrzymalibyśmy w wyniku ujemną
wartość prądu, co oznacza, że praktycznie prąd płynie w kierunku przeciwnym do
przyjętego zwrotu prądu.
Powyższe równanie można po obustronnym przemnożeniu pr zez mianownik
przepisać w postaci:
R w1 I + R w2 I +R w3 I + R 1 I + R 2 I = E 1 - E 2 + E 3 .
Po lewej stronie równania występują spadki napięć na opornikach i
rezystencjach wewnętrznych źródeł, a po prawej stronie ich siły
elektromotoryczne ze znakiem + albo -. Można je uważać za rozszerzone prawo
Ohma w obwodzie zamkniętym.
Suma spadków napięć na w szystkich elementach rezystencyjnych obw odu
nierozgałęzionego prądu stałego jest rów na sumie działających w tym
obw odzie sił elektromotorycznych z uw zględnieniem ich znaków .
4. Regulacja prądu w obw odzie
Jak wiemy, prąd w obwodzie z jednym źródłem napięcia zależy od jego siły
elektromotorycznej i od sumy rezystencji obwodu.
Zmiana wartości siły elektromotorycznej w obwodzie prądu stałego w
sposób ciągły jest w prak tyce niedogodne i dlatego rzadko stosowana. Przy
użyciu ogniw elektrochemicznych lub akumulatorów można by przez włączenie
odpowiedniej ich liczby otrzymywać różne wartości siły elektromotorycznej
skokami np. co 1,5V.
Bardziej dogodne jest nastawienie żąd anej wartości prądu przez zmianę
rezystencji obwodu. Do tego celu używamy oporników nastawnych, np.
suwakowych.
4
5
5. Stan jałow y i stan zw arcia źródła napięcia
Prąd w obwodzie złożonym z jednego źródła napięcia o danych E i R w oraz
jednego opornika R wyraża się wzorem
I=
E
Rw + R
i ma zwrot zgodny ze zwrotem siły elektromotorycznej E.
Pytamy się, jaką wartość ma napięcie V mierzone na zaciskach A i B źródła
napięcia zasilającego odbiornik prądem I?
Chcąc obliczyć napięcie V między zaciskami A i B musi my od siły
elektromotorycznej E odjąć spadek napięcia R w I na rezystencji wewnętrznej
źródła:
V = E - RwI
Stan, w którym źródło napięcia zasila odbiorniki, nazyw amy stanem
obciążenia źródła napięcia.
Stan jałow y źródła napięcia jest to taki stan, w którym przez źródło prąd nie
płynie, tj. I = 0 A.
Napięcie stanu jałow ego U o na zaciskach źródła napięcia jest rów ne jego
sile elektromotorycznej E.
E = Uo
Stan zw arcia napięcia jest to taki stan, w którym napięcie na zaciskach
źródła jest rów ne zeru, a płynący prąd „I” przyjmuje maksymalną w artość;
jest on ograniczony tylko przez rezystancję w ew nętrzną źródła; w tym stanie
pracy źródła mów imy o jego maksymalnej w ydolności prądow ej - to znaczy,
że z tego źródła w iększego prądu już się nie otrzyma.
W przypadku idealnego źródła, to jest takiego, którego oporność
w ew nętrzna byłaby rów na zero, maksymalny prąd zw arciow y w ynosiłby
nieskończenioe w iele amperów (w ydolność prądow a byłaby nieskończenie
duża) - w rzeczyw istości takie źródło nie istnieje.
6. Dzielnik napięcia
Niekiedy zależy nam na tym, aby móc nastawiać dowolne napięcia, od zera
począwszy aż do pewnej górnej wartości V g . Do tego celu służy układ zwany
dzielnikiem napięcia czyli tzw. układ potencjometryczny. Składa się on ze źródła
napięcia o sile elek tromotorycznej E większej od U g (E>U g ) oraz opornika
5
6
suwakowego lub dwóch i więcej oporników. Napięcie V odbieramy z zacisku
połączonego z suwakiem opornika i z drugiego zacisku opornika lub z innych
oporników.
a)
U
R2
=
R2
RW1
RW1
E
+ R1 + R2
I
(proporcja) stąd:
R2
U =
RW1 + R1 + R2
E
R1
R obciążenie
U
L
b)
R1 - RX
RW1 + R1
U =
E
RW1
I
}R X
E
R1
R obciążenie
U
L
rys. 1.3 przedstawia dzielnik napięcia złożony z odrębnych oporników (a)
z opornika suwakowego (b).
Otrzymane napięcie U nie ma stałej wartości lecz zależy jeszcze od
rezystencji odbiornika (obciążenia R L ) włączonego do zacisków dzielnika.
6
E