13. Teoriogrowe Modele Konkurencji Gospodarczej

13. Teoriogrowe Modele Konkurencji Gospodarczej
Najpierw, rozważamy model monopolu.
Zakładamy że monopol wybiera ile ma produkować w danym
okresie.
Koszty produkcji wynoszą cT (q).
Cena wynikająca z popytu wyraża się następującą funkcją:
p = g (q) = d −1 (q).
1 / 31
Model Monopolu
Monopol decyduje ile zaprodukować, aby zmaksymalizować zysk.
Funkcja zysku wyraża się z(q) = pq − cT (q).
Różniczkując po q, można wyznaczyć optymalny poziom produkcji.
Należy zauważyć, że gdy monopol zna funkcję popytu, ustalenie
ceny jest równoważne ustaleniu produkcji.
2 / 31
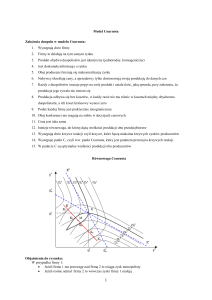
Symetryczna Gra Cournota
Gdy istnieje konkurencja, wybór ceny nie jest równoważny
wyborowi poziomu produkcji. Według teorii klasycznej, cena przy
poziomie produkcji jednej firmy też zależy od poziomu produkcji
innych firm.
Zakładamy że dwie firmy produkują identyczne dobro. Firma i
produkuje qi jednostek w danym okresie.
Cena wynika z całkowitej podaży. Zakładamy że
p = A − B[q1 + q2 ], (A, B > 0).
Tutaj, zakładamy że koszty produkcji są cT (q) = kq dla obu firm,
czyli koszty krańcowe są stałe.
Obie firmy chcą zmaksymalizować swoje zyski (czyli zysk na
jednostkę pomnożony przez podaż).
3 / 31
Symetryczna Gra Cournota
Wypłata (zysk) firmy 1 wyraża się
R1 (q1 , q2 ) = q1 [A − Bq1 − Bq2 − k] = q1 (A − k) − Bq12 − Bq1 q2 .
Z symetrii, wypłata firmy 2 wyraża się
R2 (q1 , q2 ) = q2 [A − Bq1 − Bq2 − k] = q2 (A − k) − Bq22 − Bq1 q2 .
4 / 31
Najlepsza Odpowiedź Gracza
W tym wypadku, optymalny poziom produkcji zależy od poziomu
produkcji drugiej firmy.
Przy poziomie produkcji drugiej firmy, możemy wyznaczyć
optymalny poziom produkcji jednej firmy poprzez różniczkowanie.
Można pokazać że każde dozwolone ekstremum tych funkcji zysku
(czyli przy którym produkcja i cena są dodatnie) jest maksimum.
Niech B1 (q2 ) będzie najlepszą odpowiedzią firmy 1 na q2 .
Niech B2 (q1 ) będzie najlepszą odpowiedzią firmy 2 na q1 .
5 / 31
Równowaga Nasha w Grze Cournota
Przy równowadze Nasha (q1∗ , q2∗ ), mamy
q1∗ = B1 (q2∗ ); q2∗ = B2 (q1∗ ).
Czyli firma 1 korzysta z najlepszej odpowiedzi na poziom produkcji
firmy 2 a firma 2 korzysta z najlepszej odpowiedzi na poziom
produkcji firmy 1.
Równowaga ta spełnia układ dwóch równań liniowych
∂R1
= 0;
∂q1
∂R2
=0
∂q2
6 / 31
Przykład 13.1
Zakładamy że funkcja popytu na dane dobro wyraża się
p =3−
Q
,
1000
gdzie Q jest całkowitą podażą oraz jednostkowy koszt produkcji
jest 1.
i) Wyznaczyć optymalny poziom produkcji, cenę oraz zysk
monopolu.
ii) Wyznaczyć optymalny poziom produkcji, cenę oraz zysk dwóch
”identycznych” firm produkujących nierozróżnialne dobra.
7 / 31
Przykład 13.1
8 / 31
Przykład 13.1
9 / 31
Przykład 13.1
10 / 31
Przykład 13.1
11 / 31
Model Stackelberga - Decyzje Sekwencyjne
Model ten jest analogiczny do modelu Cournota. Jedyna różnica
jest to że jedna firma jest ”liderem” i wybiera swój poziom
produkcji zanim druga firma może go wybrać.
Druga firma obserwuje poziom produkcji pierwszej firmy, a potem
ustala swój poziom produkcji.
12 / 31
Model Stackelberga
W tym wypadku, się wyznacza równowagę za pomocą rekursji.
Firma 2 używa najlepszej odpowiedzi na poziom produkcji firmy 1.
Więc najpierw rozwiązujemy równanie
∂R2 (q1 , q2 )
= 0.
∂q2
To daje optymalną odpowiedź firmy 2 jako funkcję poziomu
produkcji pierwszej firmy, q2 = B2 (q1 ).
13 / 31
Model Stackelberga
Teraz wyznaczamy optymalną strategię firmy 1 przy założeniu że
firma 2 korzysta z tej najlepszej odpowiedzi.
Gdy firma 1 produkuje q1 , wtedy firma produkuje B2 (q1 ).
Więc możemy wyrazić zysk firmy 1 jako funkcję jednej zmiennej,
q1 , czyli R1 (q1 , B2 (q1 )).
Aby wyznaczyć optymalny poziom produkcji firmy 1,
różniczkujemy tę funkcję po q1 .
Po wyznaczeniu optymalnego poziomu produkcji firmy 1, możemy
wtedy wyznaczyć optymalny poziom produkcji firmy 2.
14 / 31
Przykład 13.2
Wyznaczyć cenę, poziomy produkcji oraz zyski firmy w
równowadze dla wersji Stackelbergowskiej gry z przykładu 13.1.
15 / 31
Przykład 13.2
16 / 31
Przykład 13.2
17 / 31
Przykład 13.2
18 / 31
Przykład 13.2
19 / 31
Model Konkurencji według Bertranda
Przy założeniach modelu Bertranda, dwie firmy ustalają cenę
swojego produktu. Produkty te są nierozróżnialne.
Zakładamy że na rynku nie ma tarcia (czyli nie ma kosztów
związanych z znalezieniem najtańszej oferty).
Przy tym założeniu, gdy firmy ustalają różne ceny, firma ustalająca
najniższą cenę zaspokaja cały popyt przy tej (niższej) cenie.
Gdy firmy ustalają tę samą cenę, obie zaspokają połowę popytu
przy tej cenie.
Jednostkowy koszt produkcji wynosi k w obu firmach.
20 / 31
Model Konkurencji według Bertranda
Gdy firma 1 ustala cenę p1 > k (czyli cena przy której osiągałaby
zyski), zawsze opłaca się drugiej firmy ustalić minimalnie niższą
cenę, aby zaspokajać cały popyt i osiągać zyski.
To powoduje że wojna cenowa prowadzi cenę do poziomu kosztu
produkcji (nie opłaca ustalić niższą cenę, bo w tym wypadku firma
tylko straci).
Więc żadna firma nie osiąga ani zysków, ani strat.
W wypadku gdy jedna firma ma niższe koszty (z założenia firma 1)
niż druga firma, wtedy firma 1 obniża cenę poniżej jednostkowego
kosztu firmy 2 i w ten sposób doprowadzi firmę 2 do opuszczenia
rynku.
21 / 31
Porównanie Modeli Cournota i Bertranda
Wnioski z modelu Cournota są bardziej rozsądne niż te z modelu
Bertranda. Z drugiej strony, można zinterpretować i zaadaptować
model Bertrand, aby otrzymać bardziej rozsądne wyniki,
mianowicie:
1. Wniosek że ”żadna firma nie osiąga zysków” należy
zinterpretować jako obie firmy osiągają zyski, ale
”wystarczająco małe żeby nikt nie chce wejść na
rynek”.
2. Istnieje tarcie, czyli klienci nie mogą zawsze znaleźć
najtańszą wersję tego produktu.
3. Istnieje lojalność do danej marki. Więc nawet gdy nie
ma tarcia, klienci nie zawsze kupują najtańszą wersję
produktu.
22 / 31
Porównanie Modeli Cournota i Bertranda
Założenia 2 i 3 prowadzą do modelu, według którego w
równowadze ceny są powyżej jednostkowego kosztu produkcji, więc
obie firmy osiągają zyski.
W rzeczywistości, firmy ustalają zarówno poziom produkcji jak i
cenę.
23 / 31
Powrót do Podatków i Akcyzji
Chociaż model Stackelberga może się wydawać nienaturalny przy
modelowaniu konkurencji między firmami, zwłaszcza gdy firmy te
są podobnej wielkości, nadaje się naturalnie do teorii podatkowania.
Najpierw, rząd ogłasza wprowadzenie (lub zmianę) jakiegoś
podatku.
Firma (lub firmy) potem reaguje na to.
Wynika z tego że rząd jest naturalnym liderem Stackelbergowskim
w takich grach.
24 / 31
Powrót do Podatków i Akcyzji
Jest naturalne że firma (tutaj monopol) chce zmaksymalizować
swoje zyski.
Trudniej określić jakie są cele rządu.
W najprostszym wypadku, można założyć że rząd chce
zmaksymalizować przychód z danego podatku, czyli
zmaksymalizować tq, gdzie t jest wysokością tego podatku.
Z drugiej strony, wprowadzenie nowego podatku wpływa nie tylko
na cenę produktu, ale też na inne aspekty gospodarki (np. zysk
firmy, nadwyżkę konsumenta, przychód rządu z innych źródeł).
Ogólniej, można założyć że rząd bierze np. zysk firmy oraz
nadwyżkę konsumenta pod uwagę.
25 / 31
Powrót do Podatków i Akcyzji
Skoro firma jest z założenia monopolem, możemy przyjąć że wybór
poziomu produkcji jest równoważny wyborowi ceny.
Przy założeniu że funkcja popytu jest liniowa (lub podatek jest
mały w porównaniu do ceny), firma powinna podnieść cenę
produktu o t/2, gdzie t jest wysokość podatku.
Znając to, rząd może wybrać optymalny podatek według danego
kryterium.
Gdy funkcja popytu jest liniowa, cena w sklepie ps , cena
maksymalna (przy którym popyt całkiem się zniknie) pmax oraz
popyt w równowadze q(ps ), wtedy nadwyżka konsumenta jest
0.5q(ps )[pmax − ps ].
26 / 31
Przykład 13.3
Zakładamy że funkcja popytu na dane dobro wyraża się
następującą funkcją
q = 3000 − 1000p,
a jednostkowy koszt produkcji jest 1.
i) Pokazać że gdy nałożono podatek o wysokości t na jednostkę,
cena sklepowa będzie 2 + t/2.
ii) Przy założeniu że rząd chce zmaksymalizować przychód z
akcyzji na ten produkt, wyznaczyć odpowiedni podatek.
iii) Przy założeniu że rząd chce zmaksymalizować sumę przychodu
z akcyzji i nadwyżki konsumenta, wyznaczyć odpowiedni podatek.
27 / 31
Przykład 13.3
28 / 31
Przykład 13.3
29 / 31
Przykład 13.3
30 / 31
Przykład 13.3
31 / 31