1) Dany jest prostokąt ABCD. Bok AB podzielono na trzy równe odcinki

 GEOMETRYCZNE
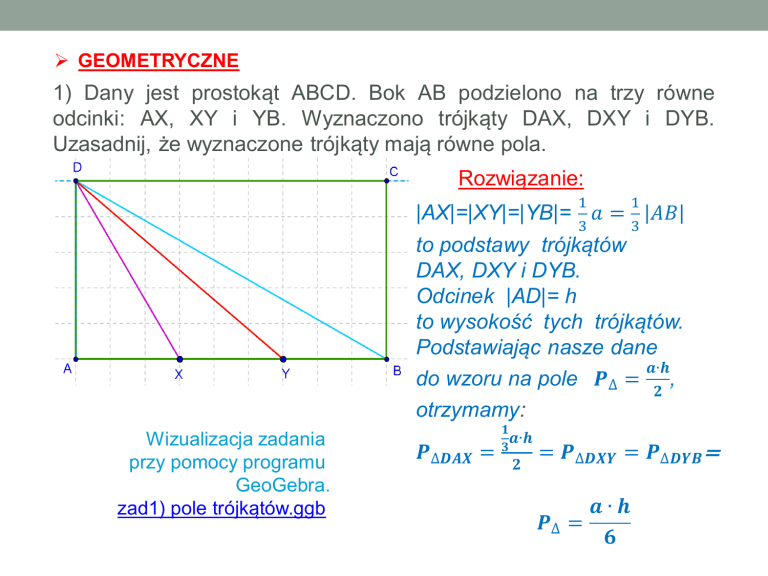
1) Dany jest prostokąt ABCD. Bok AB podzielono na trzy równe
odcinki: AX, XY i YB. Wyznaczono trójkąty DAX, DXY i DYB.
Uzasadnij, że wyznaczone trójkąty mają równe pola.
Rozwiązanie:
1
1
|AX|=|XY|=|YB|= 𝑎 = 𝐴𝐵
3
3
to podstawy trójkątów
DAX, DXY i DYB.
Odcinek |AD|= h
to wysokość tych trójkątów.
Podstawiając nasze dane
𝒂∙𝒉
do wzoru na pole 𝑷∆ = ,
𝟐
otrzymamy:
Wizualizacja zadania
przy pomocy programu
GeoGebra.
zad1) pole trójkątów.ggb
𝑷∆𝑫𝑨𝑿 =
𝟏
𝒂∙𝒉
𝟑
𝟐
= 𝑷∆𝑫𝑿𝒀 = 𝑷∆𝑫𝒀𝑩=
𝒂∙𝒉
𝑷∆ =
𝟔
2) Na rysunku AB||CD. Udowodnij, że 𝛼 + 𝛾 = 𝛽
Rozwiązanie:
Zastosowanie twierdzenia
o kątach naprzemianległych
Wizualizacja zadania
przy pomocy programu
GeoGebra
Zad2) odcinki równoległe i kąty.ggb
Rozwiązanie:
3) Punkt E leży na ramieniu BC trapezu ABCD, w którym AB∥CD.
Udowodnij, że |∡AED|=|∡BAE|+|∡CDE|.
Rozwiązanie:
Wizualizacja zadania
przy pomocy programu
GeoGebra
Zad3) trapez i punkt E na ramieniu.ggb
Zastosowanie twierdzenia o kątach naprzemianległych.
Rozwiązanie:
4) Udowodnij, że 𝛼 = 𝛽 + 𝛾 + 𝛿
Rozwiązanie:
Zastosowanie twierdzenia
o kątach naprzemianległych
i odpowiadających
Wizualizacja zadania
przy pomocy programu GeoGebra
zad4) kąty w trójkątach.ggb
Rozwiązanie:
5) Dany jest okrąg jak na rysunku. Punkty C, D, E, O są współliniowe.
Punkty A, B, C też są współliniowe. Długość odcinka BC jest równa
promieniowi okręgu. Udowodnij, że 3𝛼 = 𝛽
Rozwiązanie:
Zastosowanie
właściwości trójkątów
i kątów przyległych
Wizualizacja zadania
przy pomocy programu GeoGebra
zad5) okrąg i katy.ggb
Rozwiązanie:
𝑨𝑶 = 𝑩𝑶 = 𝑩𝑪 = 𝒓
∆ AOB i ∆ OCB to trójkąty równoramienne
𝜸 = 𝟏𝟖𝟎𝒐 − 𝟐𝜶
𝜹 = 𝟏𝟖𝟎𝒐 − 𝟏𝟖𝟎𝒐 − 𝟐𝜶 = 𝟐𝜶
𝜺 = 𝟏𝟖𝟎𝒐 − 𝟐𝜹 = 𝟏𝟖𝟎𝒐 − 𝟒𝜶
𝜶 + 𝜺 + 𝜷 = 𝟏𝟖𝟎𝒐 kąty przyległe
𝜷 = 𝟏𝟖𝟎𝒐 − 𝜶 − 𝜺
𝜷 = 𝟏𝟖𝟎𝒐 − 𝜶 − 𝟏𝟖𝟎𝒐 − 𝟒𝜶
po wykonaniu przekształceń
algebraicznych otrzymamy:
𝜷 = 𝟑𝜶
c.n.d.
6) Na rysunku przedstawiono trzy półproste o początkach w wierzchołkach
trójkąta. Udowodnij, że 𝛼 + 𝛽 + 𝛾 = 360𝑜
Rozwiązanie:
Zastosowanie
właściwości trójkątów
Wizualizacja zadania
przy pomocy programu GeoGebra
zad6) trójkąt i kąty zewnętrzne.ggb
Rozwiązanie:
7) Udowodnij, że kąt ostry wyznaczony przez przekątne prostokąta
ma miarę dwa razy większą od miary kąta, który tworzy przekątna
z dłuższym bokiem prostokąta.
Rozwiązanie:
Zastosowanie twierdzenia
o kątach naprzemianległych,
wierzchołkowych i przyległych
Wizualizacja zadania
przy pomocy programu GeoGebra
zad7) prostokąt i przekątne.ggb
Rozwiązanie:
8) Uzasadnij, że oba kąty przy podstawie AB
trójkąta równoramiennego ABC są równe.
Rozwiązanie:
Zastosowanie
właściwości trójkątów
I kątów przyległych
Wizualizacja zadania
przy pomocy programu GeoGebra
zad8) trójkąt i kąty wewnętrzne.ggb
Rozwiązanie:
9) Na rysunku przedstawiono dwa równoległoboki ABCD i ABEF.
Uzasadnij, że czworokąty CDAG oraz EFGB mają równe pola.
Rozwiązanie:
Wizualizacja zadania
przy pomocy programu GeoGebra
zad9) równoległoboki i pola.ggb
Zastosowanie
wzorów na pola
równoległoboku i trójkąta
Rozwiązanie:
Pola wielokątów:
𝑷𝑨𝑩𝑪𝑫 = 𝑷𝑨𝑩𝑬𝑭 = 𝒂 ∙ 𝒉𝒓
𝑷∆𝑨𝑩𝑮 =
𝒂 ∙ 𝒉∆
𝟐
𝑷𝑫𝑪𝑮𝑨 = 𝒂 ∙ 𝒉𝒓 −
𝑷𝑬𝑭𝑮𝑩
𝒂 ∙ 𝒉∆
𝟐
𝒂 ∙ 𝒉∆
= 𝒂 ∙ 𝒉𝒓 −
𝟐
𝑷𝑫𝑪𝑮𝑨 = 𝑷𝑨𝑩𝑪𝑫 − 𝑷∆𝑨𝑩𝑮
co oznacza, że
𝑷𝑬𝑭𝑮𝑩 = 𝑷𝑨𝑩𝑬𝑭 − 𝑷∆𝑨𝑩𝑮
𝑷𝑫𝑪𝑮𝑨 = 𝑷𝑬𝑭𝑮𝑩
c.n.d.
• ALGEBRAICZNE
1) Wykaż, że liczba 𝒂 = 𝟑𝟐𝟕 + 𝟑𝟐𝟗 jest podzielna przez 30.
Rozwiązanie:
Stosujemy przekształcenia algebraiczne:
• Wyłączanie wspólnego czynnika przed nawias
oraz działania na potęgach,
𝒂 = 𝟑𝟐𝟕 + 𝟑𝟐𝟗
𝒂 = 𝟑𝟐𝟕 𝟏 + 𝟑𝟐
𝒂 = 𝟑𝟐𝟕 ∙ 𝟏𝟎 = 𝟑𝟐𝟔 ∙ 𝟑 ∙ 𝟏𝟎
• Liczba 𝟑𝟐𝟕 dzieli się przez 3, a więc iloczyn 𝟑𝟐𝟕 ∙ 10
dzieli się przez 3 i 10, tzn. że dzieli się przez 30.
co należało udowodnić
2) Wykaż, że suma trzech kolejnych parzystych liczb naturalnych
jest podzielna przez 6.
Rozwiązanie:
• Zapisujemy liczby w postaci wyrażenia algebraicznego
jeżeli n jest dowolną liczbą naturalną
to 2n jest dowolną liczbą parzystą,
a 2n + 2 i 2n + 4 jest kolejnymi liczbami parzystymi
• Zapisujemy sumę tych liczb parzystych i stosujemy
przekształcenia algebraiczne:
𝟐𝐧 + 𝟐𝒏 + 𝟐 + 𝟐𝒏 + 𝟒 = 𝟔𝒏 + 𝟔 = 𝟔 ∙ 𝒏 + 𝟏
co należało udowodnić.
3) Napisz dowolną liczbę dwucyfrową i dopisz z jej prawej strony
liczbę lustrzaną, np.: dana jest 21 jej liczba lustrzana to 12 czyli
otrzymamy liczbę 2112.
Czy każda tak utworzona liczba dzieli się przez 11?
Sprawdź to na kilku innych przykładach.
Rozwiązanie:
• Zapiszmy kilka liczb zgodnie z poleceniem: 4334, 5445 i 7117
• Aby znaleźć dzielniki możemy wykonać rozkład danych liczb
na czynniki pierwsze
W każdym rozkładzie
widać, że liczba 11 jest
4334 2
5445 3
7117 11
jednym z dzielników
2167 11
1815 3
647 647
danych liczb.
197 197
605 5
1
1
121 11
11 11
1
co należało sprawdzić.
4) Napisz trzy dowolne cyfry. Utwórz z nich liczbę trzycyfrową
największą i najmniejszą. Różnica tych liczb jest podzielna przez 9.
Czy to prawda czy fałsz? Sprawdź, to na kilu przykładach.
Rozwiązanie:
• Zapisujemy dowolne cyfry np.: 7, 4, 9.
• Liczba najmniejsza to 479 a największa to 974.
• Różnica tych liczb: 974 – 479 = 495
• Sprawdzając cechę podzielności liczb przez 9,
otrzymamy sumę cyfr liczby 4 + 9 + 5 = 18
to znaczy, że liczba 495 dzieli się przez 9.
• Inne przykłady:
•
1) dowolne cyfry: 5, 8, 3
liczba najmniejsza to 358 a największa to 853
różnica tych liczb: 853 – 358 = 495
suma cyfr liczby 4 + 9 + 5 = 18
to znaczy, że liczba 495 dzieli się przez 9.
2) dowolne cyfry: 2, 8, 6
862 – 268=594
5 + 9 + 4 = 18
9 jest dzielnikiem liczby 594
Przyjrzyj się powyższym rozważaniom i podaj spostrzeżenia.
𝟑𝟑𝟑
5) Czy można skrócić ułamek
?
𝟏𝟎𝟓 −𝟏
Rozwiązanie:
• W pierwszej kolejności należy mianownik ułamka
doprowadzić do najprostszej postaci,
tzn. wykonać potęgowanie a następnie odejmowanie:
𝟏𝟎𝟓 − 𝟏 = 𝟏𝟎𝟎𝟎𝟎𝟎 − 𝟏 = 𝟗𝟗𝟗𝟗𝟗
•
𝟑𝟑𝟑
𝟏𝟎𝟓 −𝟏
=
𝟑𝟑𝟑
𝟗𝟗𝟗𝟗𝟗
=
𝟑𝟕
𝟏𝟏𝟏𝟏𝟏
co należało wykonać.
6) Jak jest ostatnia cyfra liczby, która jest wynikiem działania
𝟑𝟕𝟒 − 𝟒𝟏𝟕 + 𝟕𝟐𝟓 .
Rozwiązanie:
Należy ustalić ostatnie cyfry kolejnych potęg danych w działaniu:
• 𝟑𝟕𝟒
31 = 3
35=4+1 = 24𝟑
32 = 9
36=4+2 = 72𝟗
33 = 27
37=4+3 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟕
34 = 81
38=2∗4+0 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟏
Potęgę 74 dzielimy przez 4 i otrzymamy wynik 18 reszty 2
Reszta 2 oznacza, że ostatnia cyfrą potęgowania liczby 3 jest cyfra 9
• 𝟒𝟏𝟕
41 = 4
45=4+1 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟒
42 = 16
46=4+2 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟔
43=2+1 = 64
47=4+3 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟒
44=2∗2+0 = 256 48=2∗4+0 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟔
Potęgę 17 dzielimy przez 2 i otrzymamy wynik 8 reszty 1
Reszta 1 oznacza, że ostatnia cyfrą potęgowania jest cyfra 4
• 𝟕𝟐𝟓
71 = 7
75=2∗2+1 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟕
72 = 49
76=3∗2+0 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟗
73=2+1 = 147
77=3∗2+1 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟕
74=2∗2+0 = 1029 78=2∗4+0 = 𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎 𝑐𝑦𝑓𝑟𝑎 𝑡𝑜 𝟗
Potęgę 25 dzielimy przez 2 i otrzymamy wynik 12 reszty 1
Reszta 1 oznacza, że ostatnia cyfrą potęgowania jest cyfra 7
a więc ostatnią cyfrą działania 𝟑𝟕𝟒 − 𝟒𝟏𝟕 + 𝟕𝟐𝟓 jest ostatnia cyfra
wyniku sumy ostatnich cyfr poszczególnych potęg, tzn.:
9 - 4 + 7 = 12 a więc jest to cyfra 2
co należało wykonać.
7) Czy różnica między liczbą czterocyfrową, której cyfrą dziesiątek
jest zero, a liczbą zapisaną za pomocą tych samych cyfr,
ale w odwrotnej kolejności, jest podzielna przez 9?
Rozwiązanie:
• Zapisujemy liczby 2307 i 7032,
• badamy ich różnicę 7032 – 2307 = 4725
• Sprawdzamy cechę podzielności liczby przez 9,
otrzymamy sumę cyfr liczby 4 + 7 + 2 + 5 = 18
to znaczy, że liczba 4725 dzieli się przez 9.
• Inne przykłady:
1) dowolne liczby: 1608 i 8061
różnica tych liczb: 8061 – 1608 = 6453
suma cyfr liczby 6 + 4 + 5 + 3 = 18
to znaczy, że liczba 6453 dzieli się przez 9.
2) dowolne liczby: 2307 i 7032
7032 – 2307= 4725
4 + 7 + 2 + 5 = 18
9 jest dzielnikiem liczby 4725
co należało udowodnić.
8) Znajdź cyfrę A, dla której iloczyn AA・99 jest liczbą czterocyfrową
o cyfrze dziesiątek równej 2.
Rozwiązanie:
• Zastosujmy prawo rozdzielności mnożenia względem
odejmowania tj. zamiast 99 podstawimy różnicę (100 – 1)
• AA ∙ 99 = AA ∙ 100 − 1 = AA00 − AA
• otrzymaliśmy zamiast iloczynu liczb AA ∙ 99
różnicę liczb (AA00 − AA ) co pozwala znacznie szybciej wyznaczyć
•
niewiadomą cyfrę A
Możemy podstawiać kolejno cyfry od 1 do 9 i znajdziemy szukaną,
którą jest A = 7
• 77 ∙ 99 = 7700 − 77 = 7623 w której cyfrą dziesiątek jest cyfra 2
co należało udowodnić.
9) Liczbę 550 przedstaw jako różnicę dwóch liczb, z których pierwsza
jest 11 razy większa od drugiej.
Rozwiązanie:
•
Jeśli jedna liczba jest 11 razy większa od drugiej liczby, to ile razy
większa od drugiej liczby jest różnica tych liczb?
•
11𝑎 − 𝑎 = 550
11𝑎 − 𝑎 = 𝑎 11 − 1 = 𝑎 ∙ 10 = 550
10 ∙ 𝑎 = 550
to znaczy, że różnica jest 10 razy większa od szukanej liczby
a więc szukaną liczbą jest 𝟓𝟓
co należało udowodnić.
10) Przedstaw liczbę 63 w postaci sumy takich dwóch liczb,
że mniejsza z nich jest równa różnicy między nimi.
Rozwiązanie:
• Powinniśmy określić ile razy większa od mniejszej liczby
powinna być większa liczba?
𝒂 + 𝒃 = 𝟔𝟑
• Jeśli 𝒂 jest mniejszą z nich, to
𝒂=𝒃−𝒂
• czyli większa z nich jest 2 razy większa od mniejszej
𝒃=𝟐∙𝒂
• a więc ich suma jest równa 𝟑 ∙ 𝒂
𝟑 ∙ 𝒂 = 𝟔𝟑
• Szukane liczby to:
𝒂 = 𝟐𝟏 i 𝒃 = 𝟒𝟐
co należało udowodnić.
11) Na podwórku są koty i sroki. Razem jest ich 20 i mają 54 nogi.
Ile jest kotów, a ile srok?
Rozwiązanie:
• Z informacji zawartych w zadaniu wiemy, że zwierząt jest 20 sztuk
• Do każdej sztuki przydzielamy po 2 nogi a zatem przydzielono 40 nóg
• Zostało nie przydzielonych 14 nóg, nie możemy przydzielić po jednej
ponieważ ani koty ani sroki nie mają po trzy nogi
• Możemy z 14 nóg przydzielić po dwie 7 stworzeniom, które będą miały
po 4 nogi tzn. że kotów jest 7 sztuk a srok (20 – 7) czyli 13 sztuk
co należało udowodnić.
12) Udowodnij, że liczba 1011 + 1012 + 1013 + 1014 jest podzielna
przez 101.
Rozwiązanie:
• Należy posłużyć się przekształceniami algebraicznymi:
𝟏𝟎𝟏𝟏 + 𝟏𝟎𝟏𝟐 + 𝟏𝟎𝟏𝟑 + 𝟏𝟎𝟏𝟒 =
= 𝟏𝟎𝟏𝟏 (𝟏 + 𝟏𝟎 + 𝟏𝟎𝟐 +𝟏𝟎𝟑 ) =
= 𝟏𝟎𝟏𝟏 ∙ 𝟏𝟏𝟏𝟏 =
= 𝟏𝟎𝟏𝟏 ∙ 𝟏𝟏𝟎𝟎 + 𝟏𝟏 =
= 𝟏𝟎𝟏𝟏 ∙ 𝟏𝟏 ∙ 𝟏𝟎𝟎 + 𝟏 =
= 𝟏𝟎𝟏𝟏 ∙ 𝟏𝟏 ∙ 𝟏𝟎𝟏
z tego wynika, że suma danych liczb dzieli się przez liczbę 101
co należało udowodnić.
13) Ile jest nieparzystych liczb dwucyfrowych?
Rozwiązanie:
•
Należy ustalić ile jest wszystkich liczb dwucyfrowych
ostatnia liczba dwucyfrowa to 99 a ostatnia jednocyfrowa to 9
•
Po odjęciu liczb jednocyfrowych od ostatniej liczby dwucyfrowej
otrzymamy 99 – 9 = 90 liczb dwucyfrowych
•
Wiemy, że co druga liczba dwucyfrowa to liczba nieparzysta
•
A więc gdy podzielimy 90 przez 2 otrzymamy ilość liczb
dwucyfrowych nieparzystych
•
90 : 2 = 45 liczb nieparzystych dwucyfrowych
co należało udowodnić.