Temat 12 Mechanizmy ewolucji

Temat 12
Mechanizmy ewolucji
Program Ewolucja
Jest to darmowy program edukacyjny, dostępny pod adresem:
http://www.staff.amu.edu.pl/~krzychu/html/index.php?page=prog
Autor programu: Krzysztof Kościński.
Program pomaga zrozumieć wiele procesów ewolucyjnych
dzięki łatwej zmianie parametrów
i przedstawianiu wyników w formie schematów i wykresów.
Wyniki modelowania są otrzymywane poprzez:
 zastosowanie ścisłych (deterministycznych) wzorów matematycznych – gdy abstrahujemy od
zjawisk losowych,

modelowanie probabilistyczne przeżywalności i reprodukcji poszczególnych osobników – gdy
uwzględniamy zjawiska losowe.
Założenia programu
Procesy ewolucji (tzn. międzypokoleniowe zmiany puli genetycznej populacji) są modelowane przy
następujących założeniach:
 rozważany gatunek jest diploidalny (podwójna ilość informacji genetycznej),
 osobniki tego gatunku rozmnażają się wyłącznie płciowo,
 rozważany gen znajduje się na autosomie (tzn. nie jest sprzężony z płcią),
 gen ten występuje w dwóch formach (ma dwa allele),
 długość pokolenia nie zależy od rozważanego genu.
Struktura genetyczna populacji – gen, allel, genotyp
Gen = jednostka dziedziczna odpowiadająca za jakąś cechę fenotypową (fragment DNA kodujący
jakieś białko).
Allel = jedna z wersji danego genu.
Genotyp osobnika (diploidalnego) = układ dwóch alleli (takich samych lub różnych) w komórkach.
Homozygota (ze względu na dany gen) = dwa takie same allele w komórkach.
Heterozygota (ze względu na dany gen) = dwa różne allele w komórkach.
Jeżeli w populacji istnieją 2 allele (A1 i A2), to każdy osobnik ma jeden z 3 możliwych genotypów:
A1A1, A1A2 lub A2A2.
Struktura genetyczna populacji – liczebność i częstość
Liczebność jakiejś grupy = liczba egzemplarzy w tej grupie. Np.:
 liczebność genotypu A1A1 = ile osobników w populacji ma ten genotyp,
 liczebność allela A2 w populacji = liczba jego sztuk, przy czym osobniki A2A2 mają 2 takie
allele, osobniki A1A2 po jednym, a osobniki A1A1 – zero.
Częstość jakiejś grupy = liczebność tej kategorii podzielona przez liczebność całkowitą. Np.:
 częstość allela A2 w populacji = liczba takich alleli podzielona przez liczbę wszystkich alleli
(liczba alleli w populacji jest 2x większa niż liczba osobników w populacji),
 częstość genotypu A1A2 = liczba osobników o takim genotypie podzielona przez liczbę
wszystkich osobników.
Struktura genetyczna populacji = częstości alleli i genotypów tej populacji.
Pula genów = zbiór wszystkich genów populacji.
Struktura genetyczna populacji – oznaczenia
Częstości alleli oznaczamy małymi literami:
p = częstość A1,
q = częstość A2.
Częstości genotypów oznaczamy dużymi literami:
P = częstość A1A1,
H = częstość A1A2,
Q = częstość A2A2.
Suma częstości wszystkich kategorii zawsze jest równa 1:
p + q = 1,
P+H+Q=1
(zakładając istnienie tylko dwóch alleli).
Zależność częstości alleli od częstości genotypów (1)
W module „Struktura genetyczna populacji” przeprowadzono analizę składu genetycznego populacji
dla wybranych liczebności genotypów (np. po 100 osobników z każdego genotypu – dla
uproszczenia).
Analiza ta pokazuje, że częstości alleli jednoznacznie wynikają z częstości genotypów.
Zależności te są opisane wzorami:
p=P+H/2
oraz
q=Q+H/2
Zależność częstości alleli od częstości genotypów (2)
Powyższe wzory można sprawdzić na przykładzie empirycznym.
U pewnej liczby pawianów masajskich i pawianów płaszczowych zbadano grupę krwi w układzie
MN i uzyskano następujące liczebności:
Grupa krwi
Genotyp
M
MN N
MM MN NN
Pawian masajski
475
89
5
Pawian płaszczowy
223 385 129
Analiza genetyczna każdej populacji w module „Struktura genetyczna populacji” prowadzi do takich
samych wyników jak powyższe wzory, co potwierdza ich trafność.
Częstości alleli a częstości genotypów – jednoznaczność zależności
Analizy w module „Struktura genetyczna populacji” prowadzą do wniosków:
1. Dwie populacje o równych częstościach genotypów nie mogą mieć różnych częstości alleli.
2. Dwie populacje o równych częstościach alleli mogą mieć różne częstości genotypów.
Innymi słowy:
1. Z częstości genotypów jednoznacznie wynikają częstości alleli.
2. Z częstości alleli NIE wynikają jednoznacznie częstości genotypów.
Czyli:
P, H, Q  p, q

p, q  P, H, Q
Populacja wyidealizowana
Chociaż częstości genotypów nie wynikają jednoznacznie z częstości alleli,
to można je przewidywać na podstawie częstości alleli,
JEŻELI poczyni się szereg założeń odnośnie do populacji.
Wprowadzono pojęcie populacji wyidealizowanej; w populacji tej:
 nie ma migracji: osobniki nie emigrują z populacji ani imigrują do niej,
 nie zachodzi mutacja, tzn. rozważany gen nie mutuje,
 nie działa selekcja (brak doboru naturalnego), tzn. przeżywalność i reprodukcja osobników nie
zależy od rozważanego genu,
 nie ma doboru płciowego, tzn. osobniki kojarzą się w sposób całkowicie losowy,
 liczebność jest bardzo duża, wręcz dążąca do nieskończoności  niewielka rola przypadku.
Prawo Hardy’ego-Weinberga (1)
Na początku 20w. Hardy i Weinberg sformułowali prawo mówiące,
jakie są częstości genotypów w populacji wyidealizowanej,
przy zadanych częstościach alleli:
P=p
2
H = 2.p.q
Q=q
2
Prawo Hardy’ego-Weinberga (2)
Zagadnienie to można analizować w module „Prawo Hardy’ego-Weinberga”.
Krok 1: Podajemy częstości genotypów w pokoleniu rodzicielskim.
Program oblicza częstości alleli w tym pokoleniu.
Krok 2: Program oblicza częstości alleli u produkowanych (haploidalnych) gamet –
są takie same jak częstości alleli w pokoleniu rodzicielskim (p, q).
Krok 3: Gamety łączą się losowo, dając zygoty o genotypach A1A1, A1A2 i A2A2
2
2
z częstościami p , 2pq i q .
Krok 4: Wskutek rozwoju zygot powstaje pokolenie potomne.
W pokoleniu potomnym:
 częstości alleli są takie same jak w pokoleniu rodzicielskim,
 częstości genotypów są zgodne z prawem Hardy’ego-Weinberga, obojętnie jakie były w
pokoleniu rodzicielskim.
Prawo Hardy’ego-Weinberga (3)
W następnych pokoleniach potomnych nie będą już zachodzić żadne zmiany struktury genetycznej.
Zatem, w populacji wyidealizowanej:
1. Z pokolenia na pokolenie nie zachodzą zmiany częstości alleli.
2. Z pokolenia na pokolenie mogą zajść zmiany częstości genotypów. Efektem tych zmian jest
zgodność częstości genotypów w pokoleniu potomnym ze wzorami Hardy’ego-Weinberga. W
dalszym ciągu częstości genotypów już się nie zmieniają – populacja jest w stanie równowagi
genetycznej.
3. Częstości genotypów wynikają z częstości alleli.
Jeżeli populacja jest wyidealizowana, to jest w stanie równowagi genetycznej, ale
populacja nie-wyidealizowana też może się znajdować w takiej równowadze,
jeżeli np. selekcja i migracja równoważą.
Prawo Hardy’ego-Weinberga – zadanie 1
Czy populacje pawiana masajskiego i płaszczowego znajdują się w stanie równowagi Hardy’egoWeinberga ze względu na grupę krwi MN?
Pawian masajski
Grupa krwi
Pawian płaszczowy
M
MN
N
M
MN
N
Genotyp
MM
MN
NN
MM
MN
NN
Liczebność
475
89
5
223
385
129
Częstości
0,835
0,156
0,009
0,303
0,522
0,175
Częstości w pokoleniu potomnym
0,834
0,159
0,008
0,318
0,492
0,190
Program oblicza częstości genotypów w pokoleniu potomnym zgodnie z prawem H-W.
Częstości genotypów pomiędzy pokoleniem rodzicielskim a potomnym są (prawie) takie same u
pawiana masajskiego, ale nie u pawiana płaszczowego.
Prawo Hardy’ego-Weinberga – zadanie 1 (cd.)
Wnioski:
 tylko populacja pawiana masajskiego jest w stanie równowagi Hardy’ego-Weinberga,
 widocznie u pawiana płaszczowego na grupę krwi MN działa któryś z czynników wykluczonych
w definicji populacji wyidealizowanej, np. selekcja, migracja, zjawiska losowe (dryf).
Bez pomocy programu zadanie to można rozwiązać, sprawdzając czy równania H-W są spełnione
dla danej populacji:
 obliczyć częstości genotypów: liczebność genotypu podzielić przez liczebność całkowitą,
 obliczyć częstości alleli: p = P + H / 2 , q = Q + H / 2,
2
2
 obliczyć częstości genotypów: P = p , H = 2pq , Q = q .
Jeżeli tak obliczone częstości genotypów są zgodne częstościami faktycznymi,
to populacja jest w stanie równowagi genetycznej.
Prawo Hardy’ego-Weinberga – zadanie 2
Albinizm jest cechą determinowaną przez allel recesywny. Częstość występowania albinizmu u
szympansa wynosi raz na 20 tysięcy razy. Jaka jest częstość allela na albinizm oraz jaka jest częstość
nosicieli allela na albinizm? Załóż, że gen albinizmu znajduje się w populacji w stanie równowagi
genetycznej.
Allel recesywny = ujawnia się fenotypowo tylko, gdy osobnik ma dwa takie allele.
A1 – allel normalny (produkcja ciemnego barwnika),
A2 – allel na albinizm.
Albinosami są tylko osobniki o genotypie A2A2.
Nosiciel = osobnik posiadający allel na daną cechę, ale nie posiadający tej cechy (fenotypowo).
Nosicielami albinizmu są osobniki o genotypie A1A2.
Prawo Hardy’ego-Weinberga – zadanie 2 (cd.)
Dane: częstość genotypu A2A2, czyli Q = 1/20.000.
Szukane:
 częstość allela A2 czyli q,
 częstość heterozygot czyli H.
2
Skoro Q = q , to q = Q = 1/20.000 ≈ 1/141. Czyli 1 allel 141 jest zmutowany (na albinizm).
Częstość allela normalnego to: p = 1 – q = 140/141.
Częstość nosicieli: H = 2pq = 2  (140/141)  (1/141) = 280/20.000 ≈ 1/71.
Czyli, jeden osobnik na 71 jest nosicielem allela na albinizm (choć tylko jeden na 20.000 jest
albinosem).
Populacja wyidealizowana a proces ewolucji
Ewolucja = międzypokoleniowe zmiany struktury genetycznej populacji.
Innymi słowy, populacja nie jest w stanie równowagi genetycznej.
Czynniki ewolucji (tzn. jej przyczyny): dobór naturalny, mutacje, migracje, dryf genetyczny.
O populacji mówimy, że ewoluuje, niezależnie od tego, który czynnik odpowiada za jej zmiany.
W populacji wyidealizowanej nie działa żaden czynnik ewolucyjny  populacja taka nie ewoluuje.
Może jednak istnieć populacja nie-wyidealizowana, która też nie ewoluuje, np. jeżeli selekcja i
migracja równoważą.
Emigracja
Można wyróżnić dwa typy migracji:
 emigracja = opuszczanie populacji przez jej osobniki (osobniki przechodzą do innych populacji),
 imigracja = przybywanie osobników do rozważanej populacji z innych populacji.
Emigracja zmienia strukturę genetyczną populacji, jeżeli jest wybiórcza, tzn. prawdopodobieństwo
wyemigrowania każdego osobnika zależy od jego genotypu.
Jeżeli, na przykład, allel A2 powoduje zwiększenie mobilności osobnika, to najczęściej będą
emigrować osobniki o genotypie A2A2, rzadziej – A1A2, a najrzadziej A1A1. Emigracja będzie
wówczas obniżać częstość allela A2 w populacji.
Imigracja (1)
Wpływ imigracji na strukturę genetyczną populacji można analizować w module „Migracja”.
Istotne są 3 parametry:
 częstość allela A2 (q) w populacji, do której imigrują osobniki,
 częstość allela A2 (qm) u imigrantów (osobników, które przybywają do rozważanej populacji),
 frakcję imigrantów (m): jaką część populacji stanowią imigranci (z jednego pokolenia); jeżeli w
każdym pokoleniu przybywa do populacji 10 imigrantów, a populacja ma niezmiennie 1000
osobników, to m = 0,01.
Program przedstawia strukturę genetyczną populacji w trzech krokach:
Krok 1: Przed imigracją.
Krok 2: W czasie imigracji – imigranci przybyli do populacji, ale ich pula genów jest odrębna.
Krok 3: Po migracji – imigranci (i ich geny) zintegrowali się z osobnikami rdzennymi.
Imigracja (2)
Naciskając przycisk „Następne pokolenie” poznajemy częstości alleli w populacji po kolejnych
pokoleniach zachodzenia imigracji.
Symulacje procesu imigracji z różnymi wartościami początkowymi (q, qm, m) i wielokrotnym
naciskaniem powyższego przycisku prowadzą do następujących wniosków:
 Jeżeli częstość danego allela jest większa u imigrantów niż w populacji to częstość ta będzie się
zwiększać w populacji.
Jeżeli jest mniejsza u imigrantów to jego częstość w populacji będzie się zmniejszać.
 Po wielu pokoleniach imigracji, częstość allela w populacji zrówna się z częstością u imigrantów
(dokładniej: będzie się do niej asymptotycznie przybliżać).
 Szybkość zmian w częstościach alleli w populacji jest tym większa im:
– większa jest frakcja imigrantów,
– większa jest różnica pomiędzy częstością allela w populacji a częstością u imigrantów,
 Imigracja może być silnym czynnikiem ewolucyjnym (powodować szybkie zmiany w populacji).
Mutacja (1)
Mutacja = zmiana materiału genetycznego osobnika (komórki), inna niż crossing-over.
Istnieje kilka typów mutacji; tu ograniczymy się do mutacji genowych: jeden allel mutuje w inny.
Allel A1 mutuje w allel A2 z częstością u.
Allel A2 mutuje w allel A1 z częstością v.
Częstość mutowania jednego allela w inny = prawdopodobieństwo takiej mutacji danego allela w
jednym pokoleniu.
-6
Np. v = 10 = 0,000001 = w danym pokoleniu jeden allel A1 na milion mutuje w allel A2.
Mutacje zmieniają częstości alleli w populacji.
Np. mutacja A1  A2 powoduje wzrost częstości allela A2, a spadek częstości allela A1.
Mutacja (2)
Przy danych częstościach mutowania (u, v), częstość równowagowa allela A2 (qe) wynosi:
qe = u / (u + v)
Gdyby w populacji mutacje były jedynym czynnikiem wpływającym na częstości alleli, to po wielu
pokoleniach częstości alleli przyjęłyby wartość qe oraz pe (= 1 – qe).
Np.:
-5
u = 10 ,
-6
v = 10 ,
-5
-5
-6
-6
-6
-6
-6
-6
qe = 10 / (10 + 10 ) = 1010 / (1010 + 10 ) = 1010 / 1110 = 10/11 = 0,909.
Mutacja (3)
W module „Mutacja” można śledzić zmiany struktury genetycznej populacji przez wiele pokoleń
przy zadanych częstościach mutowania (u, v) i początkowych częstościach alleli (p0, q0).
Zmiany te są przedstawione na wykresie:
oś X – kolejne pokolenia potomne,
oś Y – częstości alleli lub genotypów.
Mutacje (4)
Symulacje te prowadzą do następujących wniosków:
 Po wielu pokoleniach częstości alleli w populacji osiągną wartości równowagowe (dokładniej:
będą się do nich asymptotycznie przybliżać): q = u / (u + v) , p = v / (u + v).
 Jeżeli aktualna częstość allela jest większa niż równowagowa to częstość ta będzie się w populacji
zmniejszać; jeżeli częstość aktualna jest mniejsza od równowagowej to będzie się zwiększać.
 Szybkość zmian częstości alleli w populacji jest tym większa im:
– (przede wszystkim) większą liczbą jest większa z dwóch częstości mutowania (u i v),
– (w dużym stopniu) większa jest różnica między aktualną a równowagową częstością allela,
– (w małym stopniu) większy jest iloraz dwóch częstości mutowania.
 Mutacja jest powolnym czynnikiem ewolucyjnym. Dla typowych częstości mutowania
-4
-8
rzędu 10 -10 potrzeba wielu tysięcy, a nawet milionów pokoleń, by pojawiły się zauważalne
zmiany w strukturze genetycznej populacji.
Dobór naturalny (1)
Dobór naturalny = selekcja naturalna:
liczba potomstwa, które zastąpi rodzica, zależy od genotypu rodzica.
Zróżnicowana liczba potomstwa może wynikać ze zróżnicowanej przeżywalności lub płodności.
Stopień przystosowania do środowiska = zdolność do przeżycia w nim i pozostawienia potomstwa.
Osobniki o pewnych genotypach są dobrze przystosowane do środowiska 
 mają więcej potomstwa 
 dobór naturalny faworyzuje (upowszechnia) allele wchodzące w skład tych genotypów.
Osobniki o innych genotypach są słabo przystosowane do środowiska 
 mają mniej potomstwa 
 dobór naturalny eliminuje allele wchodzące w skład tych genotypów.
Dobór naturalny (2)
Przy liczeniu potomstwa należy uwzględnić okres całego pokolenia, np.
 od zygot do zygot kolejnego pokolenia – w praktyce niewykonalne,
 od narodzin do narodzin kolejnego pokolenia – jest to wykonalne,
 od osiągnięcia dojrzałości płciowej do tego samego etapu u kolejnego pokolenia – wykonalne.
Przykładowe wartości:
Genotyp
A1A1
A1A2
A2A2
Liczebność
100
50
20
Łączna liczba potomstwa
200
25
50
Średnia liczba potomków
200 / 100 = 2 25 / 50 = 0,5 50 / 20 = 2,5
przypadająca na jednego rodzica
Wartość przystosowawcza i współczynnik selekcji
Wartość przystosowawcza (W) mierzy stopień przystosowania genotypu do środowiska.
Genotyp, którego nosiciele pozostawiają najwięcej potomstwa ma W = 1.
Genotyp, którego nosiciele nie pozostawiają potomstwa ma W = 0.
Pozostałe genotypy mają W między 0 a 1, proporcjonalnie liczby potomstwa.
Współczynnik selekcji (s) mierzy siłę selekcji (doboru) skierowanej przeciwko genotypowi.
Genotyp, którego nosiciele pozostawiają najwięcej potomstwa ma s = 0.
Genotyp, którego nosiciele nie pozostawiają potomstwa ma s = 1.
Pozostałe genotypy mają s między 0 a 1, proporcjonalnie liczby potomstwa.
Czyli: s = 1 – W , W = 1 – s.
Dla danych z powyższej tabeli: W(A2A2) = 1 , W(A1A1) = 0,8 , W(A1A2) = 0,2.
Rodzaje selekcji
Współczynniki selekcji (s) przeciwko genotypom w różnych typach selekcji:
Selekcja przeciw:
A1A1
A1A2
A2A2
allelowi recesywnemu
0
0
s
allelowi dominującemu
0
s
s
allelowi kodominującemu
0
między 0 a s
s
homozygotom
s1
0
s2
heterozygotom
0
s
0
W module „Selekcja” można ustawiać współczynniki selekcji (lub wartości przystosowawcze)
i obserwować na wykresie, jakie zmiany w strukturze genetycznej populacji powoduje selekcja
przez okres wielu pokoleń.
Selekcja przeciw allelowi recesywnemu
A1A1
A1A2
A2A2
Sytuacja 1: recesywny jest allel A2:
0
0
s
Sytuacja 2: recesywny jest allel A1:
s
0
0
Sytuacja 1: Analiza tego typu selekcji w module „Selekcja” prowadzi do następujących wniosków:
 Allel A2 jest eliminowany z populacji – jego częstość z pokolenia na pokolenie spada, w końcu
asymptotycznie zbliża się do częstości 0. Zmiany częstości allela A1 są „symetryczne” – jego
częstość dąży do jedności.
 Częstość genotypu A2A2 szybko spada do (niemal) zera, natomiast częstość heterozygot obniża
się powoli. Powolna eliminacja heterozygot wynika z tego, że nie działa na nie selekcja; allel A2
jest w nich „ukryty”.
 Szybkość eliminacji allela A2 jest tym większa im większy jest współczynnik selekcji dla A2A2.
Zależność ta jest z grubsza proporcjonalna (np. 2x silniejsza selekcja  2x szybsze zmiany).
 Działanie selekcji praktycznie nie zależy od początkowych częstości alleli.
Sytuacja 2: Wyniki są takie same, tylko trzeba zamienić oznaczenia A1 z A2.
Selekcja przeciw allelowi (ko)dominującemu
A1A1
A1A2
A2A2
Postać ogólna
0
s1
s2
Całkowita dominacja
0
s
s
Idealna kodominacja
0
s/2
s
s1  s2
Zmiany pod wpływem takiej selekcji są podobne jak dla selekcji przeciw allelowi recesywnemu,
lecz są znacznie szybsze, ponieważ allel A2 nie ukrywa się w heterozygotach.
By się o tym przekonać, można porównać dwie sytuacje:
A1A1
A1A2
A2A2
Sytuacja 1: selekcja przeciw allelowi recesywnemu:
0
0
0,2
Sytuacja 2: selekcja przeciw allelowi dominującemu:
0
0,01
0,2
Selekcja przeciw allelowi recesywnemu lub dominującemu – przykłady
Choroby dziedziczne determinowane przez allel recesywny:
 mukowiscydoza: produkcja lepkiego śluzu  zaburzenia gł. układu oddechowego i pokarmowego,
 fenyloketonuria: fenyloalanina nie jest przekształcana, lecz magazynowana w toksycznych ilościach,
 albinizm: brak produkcji melaniny – ciemnego barwnika w skórze, włosach i tęczówce.
Choroby dziedziczne determinowane przez allel dominujący:
 brachydaktylia: krótkie palce, zrośnięte dwa ostatnie paliczki,
 pląsawica Huntingtona: uszkodzenia mózgu – zaburzenia ruchu, otępienie.
Selekcja przeciw homozygotom
A1A1
A1A2
A2A2
s1
0
s2
s1 może być równe lub różne od s2
Analiza tego typu selekcji w module „Selekcja” prowadzi do następujących wniosków:
 Selekcja nie powoduje eliminacji żadnego allela. Częstości obu alleli dążą do wartości stabilnych
(równowagowych), które są różne od zera i od jedności.
 Częstości stabilne alleli zależą od współczynników selekcji przeciw homozygotom. Częstość
stabilna allela A2 wynosi: qe = s1 / (s1 + s2) .
 Częstości równowagowe zależą tylko od relacji między dwoma współczynnikami selekcji przeciw
homozygotom, a nie zależą od tego czy te współczynniki są duże czy małe. Innymi słowy,
częstości równowagowe nie zależą od tego jak duża jest przewaga adaptacyjna heterozygot nad
homozygotami.
 Od wielkości przewagi heterozygot nad homozygotami zależy jednak (dodatnio) szybkość
osiągania równowagowych wartości częstości (dokładniej: szybkość przybliżania się do nich).
Selekcja przeciw homozygotom – anemia sierpowata
Allel A1 determinuje produkcję normalnej hemoglobiny.
Allel A2 determinuje produkcję nieprawidłowej hemoglobiny.
Osoby o genotypie:
 A1A1 mają normalne erytrocyty (krwinki czerwone), ale są podatne na malarię,
 A1A2 mają normalne erytrocyty i są odporne na malarię,
 A2A2 są odporne na malarię, ale mają sierpowate erytrocyty  anemia sierpowata.
W rejonach, gdzie nie występuje malaria, allel A2 nie przynosi żadnych korzyści 
 został wyeliminowany (selekcja przeciw allelowi recesywnemu).
W rejonach, gdzie malaria występuje (większość Afryki, południowa Azja), częstość allela A2
stabilizuje się na poziomie kilku-kilkunastu procent.
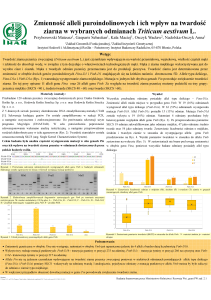
Występowanie anemii sierpowatej i malarii
występowanie anemii sierpowatej
występowanie malarii (populacje rdzenne)
Selekcja przeciw homozygotom – geny MHC
Zbiór genów MHC koduje białka, które służą do rozpoznawania ciał obcych (antygenów).
Osobnik, który jest heterozygotą na wszystkich tych genach, ma 2x więcej alleli niż osobnik
całkowicie homozygotyczny 
 wykrywa 2x więcej różnych antygenów 
 lepiej zwalcza pasożyty i drobnoustroje 
 jest zdrowszy.
Samice preferują zapach samców, które są bardziej heterozygotyczne na genach MHC.
Wykazano to dla gryzoni i ludzi  preferencja taka jest prawdopodobna też u innych naczelnych.
Selekcja przeciw heterozygotom (1)
A1A1
A1A2
A2A2
0
s
0
0
s1
s2
s1 > s2
s2
s1
0
s1 > s2
W każdym przypadku, najgorzej przystosowana jest heterozygota.
Modelowanie ewolucji pokazuje, że:
 Selekcja ta eliminuje jeden z alleli.
 To, który allel zostanie usunięty, zależy od współczynników selekcji oraz początkowych częstości
alleli. W populacji pozostanie allel, który początkowo miał odpowiednio dużą częstość.
 Jeżeli q0 to początkowa częstość allela A2, a qe = s1 / (2  s1 – s2) to:
q0 < qe  eliminacja allela A2
q0 > qe  eliminacja allela A1
q0 = qe  brak zmian.
Selekcja przeciw heterozygotom (2)
Przykład: wprowadź do okna programu następujące współczynniki selekcji:
A1A1
A1A2
A2A2
0
0,3
0,1
Częstość równowagowa A2: qe = 0,3 / (2  0,3 – 0,1) = 0,3 / 0,5 = 0,6.
Manipulacja wartościami początkowymi pokazuje, że allel A2 jest zachowywany, gdy jego
początkowa częstość jest powyżej 0,6.
Przykład empiryczny:
Dwie populacje żyją koło siebie i mają inne geny (np. jedna populacja – A1, a druga – A2).
Mieszańce między nimi są heterozygotami – oba allele mogą źle współdziałać w jednym organizmie.
Słabe przystosowanie heterozygot będzie zapobiegać rozpowszechnianiu mieszańców.
Zjawiska losowe – dryf genetyczny
Dryf genetyczny = ogół zjawisk losowych, które zmieniają strukturę genetyczną populacji (w sposób
nieprzewidywalny).
Przykłady takich zjawisk:
 heterozygota produkuje gamety A1 i A2 – nie wiadomo, która da początek zygocie,
 dobrze przystosowany osobnik może zginąć, a gorzej przystosowany – przeżyć.
Z tych powodów procesy ewolucji należy modelować probabilistycznie (uwzględniając przypadek),
a nie deterministycznie (bazować na ścisłych wzorach matematycznych).
Przypadek można pominąć jedynie w bardzo dużych populacjach (por. populacja wyidealizowana).
Modelowanie dryfu genetycznego
Skutki dryfu genetycznego można modelować w module „Dryf – jedna populacja”.
Należy podać liczebność samic i samców w populacji oraz liczbę alleli A1 i A2 u każdej płci.
Na podstawie tych danych program oblicza częstości alleli u obu płci oraz w całej populacji.
Uwaga: gdy mówimy o liczebności populacji, to chodzi tu o liczebność danego pokolenia w
populacji. Jest to szczególnie istotne dla populacji wielopokoleniowych (takich jak ludzkie).
Symulację dryfu genetycznego w populacji uruchamiamy przyciskiem „Działaj”.
Na wykresie pokazywane są zmiany częstości alleli w kolejnych pokoleniach.
Przy danych wartościach początkowych, symulację można przeprowadzić wielokrotnie poprzez
sukcesywne naciskanie przycisku „Działaj”.
Dryf genetyczny – zadanie 1
Dla domyślnych ustawień parametrów populacji przeprowadź kilka-kilkanaście symulacji.
Prowadzą one do następujących spostrzeżeń:
1. Częstości alleli zmieniają się z pokolenia na pokolenie w sposób losowy, nieprzewidywalny. Nie
można przewidzieć ani kierunku zmiany (czy częstość wzrośnie czy zmaleje), ani wielkości
zmiany (czy będzie duża, mała czy żadna).
2. W którymś pokoleniu dochodzi do całkowitej eliminacji jednego allela. Od tego momentu
populacja zawiera tylko jeden allel. Mówimy o utrwaleniu tego allela w populacji.
3. Numer pokolenia, w którym dochodzi do utrwalenia allela zależy od czynników losowych i
dlatego jest nieprzewidywalny.
4. Do momentu utrwalenia allela w populacji znajdują się zarówno homozygoty jak i heterozygoty.
Od momentu utrwalenia nie ma już heterozygot. Generalnie, dryf prowadzi do spadku częstości
heterozygot w populacji.
Dryf genetyczny – zadanie 2
Mimo, że zmiany struktury genetycznej pod wpływem dryfu są losowe, to można dostrzec pewne
prawidłowości. Sprawdź od czego i w jaki sposób zależy:
 numer pokolenia, w którym dochodzi do utrwalenia allela (czas utrwalenia),
 to czy utrwali się allel A1 czy A2.
Odpowiedzi:
1. Im większa liczebność populacji, tym przeciętnie dłuższy jest czas utrwalania allela.
2. Im częstości początkowe alleli są bliższe 0 i 1 (dalsze od 0,5), tym przeciętnie krótszy jest czas
utrwalania allela.
3. Im większa jest częstość allela w pokoleniu wyjściowym, tym większe jest prawdopodobieństwo,
że to on się utrwali (a nie drugi allel). Dokładnie: prawdopodobieństwo utrwalenia allela jest
równe jego początkowej częstości.
Dryf genetyczny – liczebność efektywna
Można przewidywać intensywność dryfu (zjawisk losowych) w danej populacji, jeżeli znana jest jej
liczebność (n) oraz częstość allela A1 (p).
W niektórych populacjach, natężenie dryfu jest jednak większe lub mniejsze niż to wynika z ich
liczebności. Na przykład, populacja o 100 osobnikach zachowuje się tak (w sensie działania dryfu)
jakby miała 90 osobników (tzn. dryf działa silniej niż to przewiduje teoria).
Liczebność efektywna populacji (ne) = liczebność, przy której teoretycznie przewidywane
natężenie dryfu jest równe faktycznie obserwowanemu dryfowi w tej populacji.
ne = n  dryf zachodzi zgodnie z teoretycznymi przewidywaniami,
ne > n  dryf zachodzi wolniej,
ne < n  dryf zachodzi szybciej.
Proporcja płci. Dla równych liczebności płci: ne = n. Im większa dysproporcja, tym mniejsza
liczebność efektywna.
Wariancja liczby potomstwa. Jeżeli wszystkie osobniki mają mniej więcej tyle samo potomków to ne
> n. Jeżeli liczba potomstwa jest mocno zróżnicowana to ne < n.
Współdziałanie czynników ewolucyjnych
Dotychczas rozważaliśmy działanie każdego czynnika ewolucyjnego osobno:
migracja, mutacja, selekcja, dryf.
W populacjach rzeczywistych czynniki te działają równocześnie.
Jakie są skutki równoczesnego działania tych czynników?
Symulacje tego typu można przeprowadzać w module „Wszystkie czynniki”. Można tutaj:
 podać liczebność populacji lub ustawić jej liczebność na „nieskończoną”,
 ustawić parametry migracji, mutacji, selekcji,
 włączać i wyłączać działanie tych czynników.
Selekcja + mutacja (1)
Często jest spotykana sytuacja:
 allel A1 jest normalny (dziki), a allel A2 jest allelem zmutowanym,
 allel A2 jest recesywny – ujawnia się tylko u homozygot i obniża ich wartość dostosowawczą,
 częstość mutowania do allela szkodliwego (A2) jest znacznie większa niż częstość mutacji
wstecznej (do allela A1).
W takich warunkach mutacja będzie dążyć do zwiększenia częstości allela A2, a selekcja do jej
zmniejszenia. Jaka będzie wypadkowa działania obu czynników; który czynnik okaże się silniejszy?
W programie otwieramy plik „selekcja+mutacja”. Wczytano następujące wartości parametrów:
 Duża populacja – pomijamy dryf. Częstość alleli: 0,5.
-4
-5
 Częstości mutowania: 10 (do A2) i 10 (do A1). Są to raczej duże częstości mutowania.
 Współczynniki selekcji: umiarkowanie silna selekcja przeciw A2A2, s = 0,2.
 Migracja jest wyłączona.
Selekcja + mutacja (2)
Wynik:
Częstość allela A2 wyraźnie spada, ale nie dąży do zera. Częstość stabilna tego allela wynosi 0,022.
Przy tej częstości selekcja i mutacja równoważą się – tyle samo powstaje alleli A2, ile jest
eliminowanych (przez selekcję, ale także przez mutację wsteczną).
Wniosek:
Częstość stabilna allela zmutowanego jest niska  selekcja jest znacznie silniejszym czynnikiem
ewolucyjnym niż mutacja.
Twierdzenie to jest prawdziwe też dla innych częstości mutowania i współczynników selekcji.
Selekcja + dryf
Współdziałanie selekcji i dryfu można badać po otwarciu pliku „selekcja+dryf”:
 Mała populacja – uwzględniamy dryf. Liczebność: 1000 osobników, równość samic i samców,
częstości alleli: 0,5.
 Współczynniki selekcji: słaba selekcja przeciw A2A2, s = 0,05.
 Migracja i mutacja są wyłączone.
Wyniki:
 Częstość allela A2 spada, osiągając wartość 0 po kilkuset pokoleniach. Zatem selekcja, a nie dryf
(przypadek), decyduje o tym, który allel zostanie usunięty.
 Zmiana częstości allela jest nieregularna – przyczyną fluktuacji jest dryf. Również dryf sprawia,
że całkowita eliminacja allela A2 następuje po różnej liczbie pokoleń.
 W przeanalizowanym przykładzie zarówno dryf jak i selekcja były słabe (n = 1000, s = 0,05).
Zmieniając siłę dryfu oraz siłę selekcji można wykazać, że selekcja prawie zawsze przeważa
nad dryfem, z wyjątkiem sytuacji, gdy w małej populacji (silny dryf) działa bardzo słaba
selekcja.
Selekcja + migracja
Otwieramy plik „selekcja+migracja”. Zostają wczytane następujące parametry:
 Duża populacja – pomijamy dryf. Częstości alleli: 0,5.
 Współczynniki selekcji: przeciw A1A2 s = 0,1; przeciw A2A2 s = 0,2.
 Częstość allela A1 u imigrantów wynosi 0,1, allela A2 – 0,9. Frakcja imigrantów m = 0,01.
 Mutacja jest wyłączona.
Wyniki:
 Selekcja dąży do usunięcia allela A2 z populacji, a imigranci wnoszą głównie właśnie ten allel.
 Ustala się pewien stan równowagi – w tym przykładzie częstość stabilna allela A2 wynosi 0,081.
 Selekcja wywiera silniejszy wpływ na strukturę genetyczną populacji niż migracja, ale jest tak z
powodu małej częstości migrowania.
 Gdy frakcja imigrantów jest duża to migracja może zrównoważyć selekcję, albo nawet nad nią
górować (gdy współczynniki selekcji są niewielkie). Zatem: selekcja i migracja są z grubsza
równie silnymi czynnikami ewolucyjnymi.
Selekcja + mutacja + dryf (wersja 1)
Otwieramy plik „selekcja+mutacja+dryf(1)”:
 Mała populacja – uwzględniamy dryf. Liczebność: 1000 osobników, proporcja płci: pół na pół.
 Pula genetyczna populacji zawiera wyłącznie allel A1. Brak allela A2.
-6
-7
 Częstości mutowania są przeciętne: 10 (do A2) i 10 (do A1).
 Selekcja, i to silna, działa tylko na genotypy A1A1, s = 0,5. Allel A1 jest więc gorszy od allela A2.
 Migracja jest wyłączona.
Kilkukrotne przeprowadzenie symulacji prowadzi do obserwacji:
 Częstość allela A1 wynosi 1 aż do momentu pojawienia się, wskutek mutacji, allela A2.
 Genotypy z allelem A2 są dostosowawczo lepsze od genotypów A1A1  selekcja zwiększa
częstość allela A2, aż do całkowitego usunięcia z populacji allela A1.
Tak się dokonuje postęp ewolucyjny.
Selekcja + mutacja + dryf (wersja 2)
Otwieramy plik „selekcja+mutacja+dryf(2)”:
 Mała populacja – uwzględniamy dryf. Liczebność: 100 osobników, proporcja płci: pół na pół,
częstości alleli: 0,5.
-3
-6
 Częstości mutowania: 10 (do A2) i 10 (do A1).
 Selekcja działa tylko na genotypy A2A2, s = 0,05.
 Migracja jest wyłączona.
Wyniki symulacji:
 Selekcja eliminuje allel A2, lecz ten wciąż powraca dzięki dużej częstości mutowania.
 Silny dryf (niewielka liczebność populacji) powoduje znaczne, losowe wahania częstości alleli.
Wszystkie czynniki
Działanie wszystkich czynników ewolucyjnych równocześnie, w ich typowych natężeniach, można
obserwować po otworzeniu pliku „wszystko”:
 Mała populacja – uwzględniamy dryf. Liczebność: 1000 osobników, proporcja płci: pół na pół,
częstości alleli: 0,5.
-4
-5
 Częstości mutowania: u = 10 , v = 10 .
 Selekcja działa tylko na genotypy A2A2, s = 0,2.
 Frakcja imigrantów m = 0,01; częstość allela A2 u imigrantów qm = 0,6.
Przy takich ustawieniach:
 Częstość allela A1 waha się wokół 0,85, a allela A2 wokół 0,15. Wartości te są wypadkowymi
działania selekcji i migracji.
 Można wyłączyć samą selekcję lub samą migrację, aby zobaczyć co się dzieje, gdy będzie działać
tylko jeden z tych czynników.
 Mutacja nie wywiera istotnego wpływu (jej wyłączenie nie powoduje zauważalnych zmian).
 Nieznaczne fluktuacje częstości alleli wynikają z dryfu.
Dobór zależny od częstości (1)
Nieraz wartość przystosowawcza danego genotypu zależy od tego, jakie genotypy posiadają inne
osobniki w populacji. Innymi słowy – jakie są częstości genotypów w populacji.
Zjawisko to omówimy na przykładzie dwóch alternatywnych strategii zachowań:
 Agresor: walczy o terytorium z innym osobnikiem.
 Ustępujący: nie walczy, zajmuje jedynie wolne terytorium.
Dany osobnik, wskutek interakcji z innym osobnikiem, może odnieść korzyść (np. zdobył
terytorium) i/lub ponieść stratę (np. rany zadane w walce).
Korzyści i straty osobnika zależą od tego, jaką przyjmuje strategię (agresor / ustępujący) i jaką
strategię przyjmuje rywal (agresor / ustępujący).
Przeciętne skutki interakcji agresorów i ustępujących z rywalami zależą od tego, jak często trafiają
na agresorów, a jak często na ustępujących – czyli od częstości tych strategii w populacji.
Dobór zależny od częstości (2)
W module „Strategie ewolucyjne” można badać zależność wartości przystosowawczej strategii
agresora i ustępującego od częstości tych strategii w populacji, przy zadanych wartościach zysków i
strat, jakie można odnieść w interakcji z rywalem.
Przykładowo:
Całkowity zysk = 1,0 (zajęcie terytorium).
Całkowita strata = 1,5 (poważne rany odniesione w walce).
Agresor w kontakcie w agresorem: może wygrać lub przegrać  statystycznie ma połowę zysku i
połowę strat. Bilans takich kontaktów wyniesie więc: 0,51,0 – 0,51,5 = –0,25.
Agresor w kontakcie z ustępującym: ustępujący schodzi mu z drogi  agresor bierze cały zysk nie
ponosząc strat. Bilans: 1,01,0 – 0,01,5 = 1,0.
Ustępujący w kontakcie z agresorem: schodzi agresorowi z drogi  nie odnosi ani zysków ani strat.
Bilans: 0,01,0 – 0,01,5 = 0,0.
Ustępujący w kontakcie z ustępującym: przypadek decyduje o tym, kto zajmie terytorium  osobnik
odnosi połowę korzyści i nie ponosi strat. Bilans: 0,51,0 – 0,01,5 = 0,5.
Dobór zależny od częstości (3)
Średni bilans każdej ze strategii zależy od tego, jak często natrafia się na agresorów, a jak często na
ustępujących – czyli od częstości tych strategii w populacji.
Załóżmy, że obie strategie mają częstość równą 0,5. Wówczas:
Średni bilans agresora = –0,250,5 + 1,00,5 = 0,375.
Średni bilans ustępującego = 0,00,5 + 0,50,5 = 0,250.
Czyli agresor ma wyższą wartość przystosowawczą niż ustępujący.
Ale jeśli założymy, że częstość agresora wynosi 0,75 (ustępującego 0,25) to:
Średni bilans agresora = –0,250,75 + 1,00,25 = 0,063.
Średni bilans ustępującego = 0,00,75 + 0,50,25 = 0,125.
Czyli ustępujący ma wyższą wartość przystosowawczą niż agresor.
Dobór zależny od częstości (4)
Czyli, na ogół lepiej być agresorem niż ustępującym, ale jeśli agresorzy stanowią większość
populacji to lepiej być ustępującym.
Istnieją takie częstości obu strategii, przy których obie strategie mają taką samą wartość
przystosowawczą – jest to częstość agresora równa 2/3 (ustępującego 1/3). Wówczas:
Średni bilans agresora = –0,25(2/3) + 1,0(1/3) = 1/6.
Średni bilans ustępującego = 0,0(2/3) + 0,5(1/3) = 1/6.
Są to częstości ewolucyjnie stabilne, tzn. w toku ewolucji, częstości obu strategii będą się zmieniać
w ich kierunku. Po osiągnięciu tych wartości, nie będzie już dalszych zmian częstości strategii.
W jaki sposób NIE zachodzi ewolucja?
Wielu studentów, mimo deklarowanego odrzucania lamarkizmu, pojmuje ewolucję w sposób
lamarkowski:
Lamarck: przyroda dąży do doskonalenia się.
Student: „Geny mutują w takie allele, które w danym środowisku będą korzystne.”
W rzeczywistości mutacje są losowe, ich skutki są najczęściej niekorzystne, a rzadko korzystne.
Lamarck: cechy nabyte dziedziczą się.
Student: „Ewolucja inteligencji u przodków człowieka polegała na tym, że rodzice przekazywali swą
mądrość potomstwu, a dodatkowo dzieci zdobywały wiedzę samodzielnie. W ten sposób z pokolenia
na pokolenie populacja stawała się coraz inteligentniejsza.”
Taka kumulacja wiedzy / mądrości może zachodzić, ale nie jest to ewolucja biologiczna (co
najwyżej ewolucja kulturowa). Proces nauki nie prowadzi do żadnych zmian w genotypie. Nabyta
wiedza / mądrość nie jest więc dziedziczona w sensie biologicznym.