BADANIE ZJAWISKA HALLA

BADANIE ZJAWISKA HALLA
PYTANIA KONTROLNE
1. Efekt Halla
2. Ruch cząstki naładowanej w polu magnetycznym – siła Lorentz’a
3. Pole magnetyczne przewodnika z prądem
4. Pole magnetyczne solenoidu
5. Wykorzystanie efektu Halla
UKŁAD POMIAROWY
Celem ćwiczenia jest obserwacja efektu Halla. W układzie pomiarowym przedstawionym na
rys. 1, sonda Halla umieszczona jest w solenoidzie, przez który płynie prąd o natężeniu I. Pod
wpływem pola magnetycznego indukowanego wewnątrz solenoidu, w sondzie (przez którą
płynie prąd sterujący IS) generuje się napięcie poprzeczne UY, mierzone przy pomocy
miliwoltomierza cyfrowego. Jedną ze składowych napięcia poprzecznego jest napięcie Halla
UH, pojawiające się w układzie przy obecności zewnętrznego pola magnetycznego. Pomiar
pierwszy polega na zmierzeniu napięcia poprzecznego pojawiającego się w próbce przy
nieobecności zewnętrznego pola magnetycznego. Kolejne pomiary przeprowadza się dla
niezerowego pola magnetycznego i odejmuje się wyniki pierwszego pomiaru (↘ Dodatek).
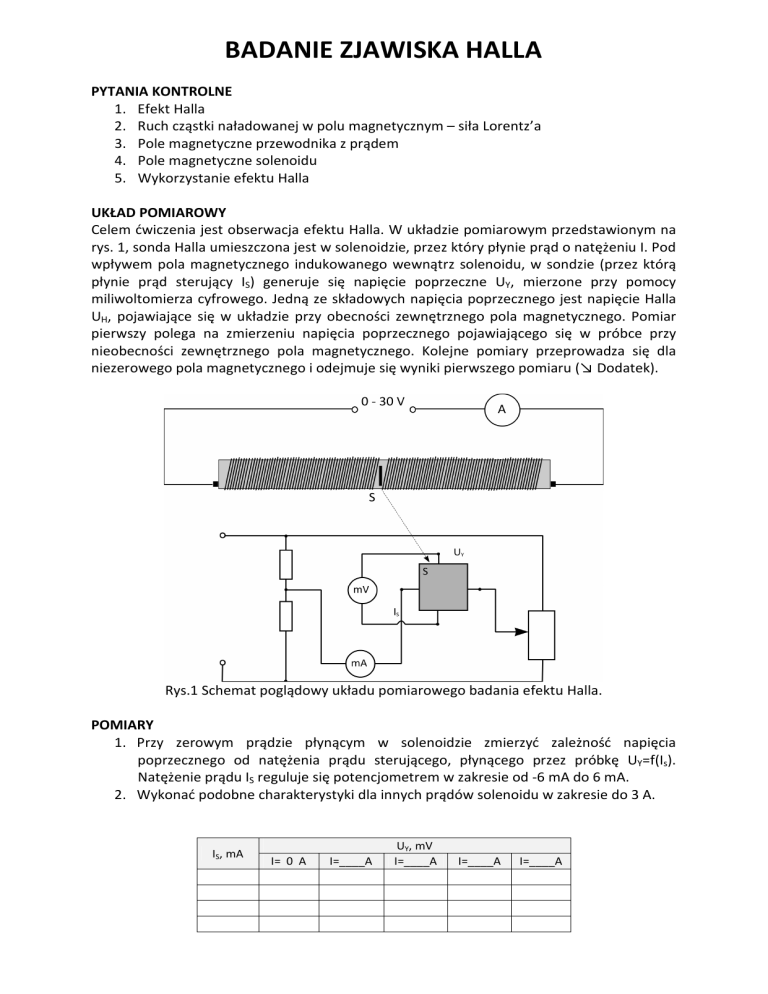
Rys.1 Schemat poglądowy układu pomiarowego badania efektu Halla.
POMIARY
1. Przy zerowym prądzie płynącym w solenoidzie zmierzyć zależność napięcia
poprzecznego od natężenia prądu sterującego, płynącego przez próbkę UY=f(Is).
Natężenie prądu IS reguluje się potencjometrem w zakresie od -6 mA do 6 mA.
2. Wykonać podobne charakterystyki dla innych prądów solenoidu w zakresie do 3 A.
IS, mA
I= 0 A
I=____A
UY, mV
I=____A
I=____A
I=____A
OPRACOWANE WYNIKÓW POMIARÓW
1. Od wszystkich napięć poprzecznych odjąć napięcie występujące przy zerowym
prądzie cewki, dla odpowiadającej wartości prądu IS. W wyniku odjęcia otrzymuje się
napięcie Halla UH.
2. Na wspólnym wykresie przedstawić zależności napięcia Halla UH w funkcji natężenia
prądu próbki IS, zmierzone dla różnych wartości.
3. Obliczyć współczynniki kierunkowe otrzymanych charakterystyk UH=a⋅IS, gdzie
AR I
a= H ,
d
A=0.0045 T/A (stała aparaturowa);
d= 0.0815(50) mm (grubość hallotronu);
4. Dla każdej charakterystyki obliczyć stałą Halla RH, pamiętając o rachunku jednostek.
5. Jakiego typu jest półprzewodnik z którego wykonano sondę Halla?
6. Korzystając z prawa przenoszenia niepewności obliczyć niepewności otrzymanych
stałych Halla.
7. Metodą średniej ważonej obliczyć wartość średnią stałej Halla wraz z niepewnością.
8. Dla każdej charakterystyki obliczyć czułość hallotronu
a
γ0 =
.
A ⋅I
9. Korzystając z prawa przenoszenia niepewności obliczyć niepewności otrzymanych
czułości.
10. Metodą średniej ważonej obliczyć wartość średnią czułości hallotronu wraz
z niepewnością.
11. Dla każdej charakterystyki obliczyć koncentrację nośników ładunku
1
n=
.
eR H
12. Korzystając z prawa przenoszenia niepewności obliczyć niepewności otrzymanych
koncentracji.
13. Metodą średniej ważonej obliczyć wartość średnią koncentracji nośników ładunku
i wyrazić ją w cm-3, wraz z niepewnością.
14. Zapisać wyniki końcowe w poprawnym formacie.
DODATEK
Napięcie poprzeczne Uy jest sumą spadków napięć, które są wywołane
przez różne efekty towarzyszące zjawisku Halla:
Uy = UH + UE + UN + URL + UA,
gdzie: UH – napięcie Halla,
UE – napięcie wywołane efektem Ettingshausena,
UN – napięcie Nernsta,
URL – napięcie Righi - Leduca,
UA – napięcie asymetrii, wynikające z asymetrycznego
ustawienia sond napięciowych na badanej próbce.
Nazwa
materiału
Li
Cu
Au
Be
In
Si
Ge
GaAs
Stała
Halla,
3
m /C
-11
-1.7⋅10
-11
-5.4⋅10
-11
-7.2⋅10
-11
24.3⋅10
-11
15.9⋅10
330
-2
5.2⋅10
6
4.4⋅10