06_Wyklad_MP

5. OBWODY PRĄDU HARMONICZNEGO
5.1. ZWIĄZKI POMIĘDZY NAPIĘCIEM I PRĄDEM
DLA ELEMENTÓW R, L, C
 REZYSTOR
Przy przepływie prądu harmonicznego
it   I m sin  t i 
(5.1)
przez rezystor o rezystancji R, na jego zaciskach pojawi się napięcie
u t   R it   R I m sin  t i   U m sin  t u 
(5.2)
przy czym amplituda przebiegu napięcia
a faza początkowa
Um  R Im
(5.3)
 u  i
(5.4)
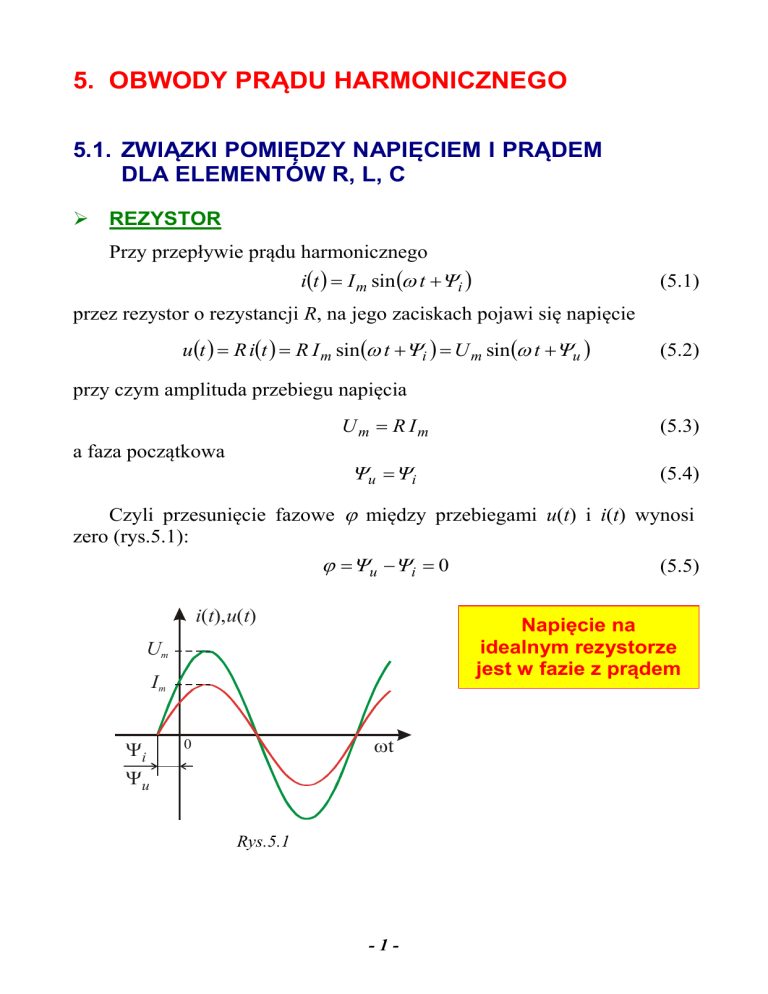
Czyli przesunięcie fazowe  między przebiegami u(t) i i(t) wynosi
zero (rys.5.1):
 u i  0
i(t), u(t)
Napięcie na
idealnym rezystorze
jest w fazie z prądem
Um
Im
i
u
t
0
(5.5)
Rys.5.1
-1-
W POSTACI SYMBOLICZNEJ
Symboliczna wartość chwilowa prądu
I m  I m e ji
(5.6)
u(t )  R i(t )  R I m e jt  U m e jt
(5.7)
Um  RIm
(5.8)
i(t )  I m e jt
napięcia
Zatem
gdzie
co oznacza, że
U  RI
I  GU
Przedstawiając symboliczne
wykładniczej, otrzymujemy
wartości
(5.9)
skuteczne
U e j u  R I e j i
w
postaci
(5.10)
Z przyrównania modułów w wyrażeniu (5.10) znajdujemy
I GU
URI
a z przyrównania argumentów
 u  i
(5.12)
U
Pomnożenie wskazu I przez R
powoduje wydłużenie tego
wskazu R razy. Wobec tego
wskaz
napięcia
U  R I znajduje się na tej
samej prostej co wskaz I
(rys.5.2)
(5.11)
I
u=i
Rys.5.2. Wykres wskazowy rezystora
-2-
 CEWKA INDUKCYJNA
W punkcie 1.7 stwierdziliśmy, że przy przepływie prądu w cewce
idealnej o indukcyjności L, napięcie na jej zaciskach wyraża zależność
(1.25)
u t   L
d it 
dt
Przyjmując, że w cewce płynie prąd harmoniczny
it   I m sin  t i 
(5.13)


ut    L I m sin  t i    U m sin  t u 
2

(5.14)
napięcie na cewce wynosi
Z powyższej zależności wynika, że amplituda przebiegu napięcia
Um   L Im
natomiast faza początkowa
 u  i 
(5.15)

(5.16)
2
Czyli przesunięcie fazowe  między przebiegami u(t) i i(t) cewki
indukcyjnej wynosi (rys.5.3):
 u i 

2
u(t), i(t)
u
i
0
(5.17)
Napięcie na zaciskach
idealnej cewki
wyprzedza prąd
o 90o
t
/2
Rys.5.3
-3-
Dla cewki indukcyjnej - symboliczna wartość chwilowa prądu
i(t )  I m e jt
napięcia
u t   L
gdzie
I m  I m e ji
(5.18)
d it 
 j  L I m e j t  U m e j t
dt
Zatem
(5.19)
U m  j L I m
(5.20)
co oznacza, że
U  j L I
I
Przedstawiając symboliczne
wykładniczej, otrzymujemy
1
j L
wartości
U e ju   L
U
(5.21)
skuteczne
w


j  i  
I e  2
postaci
(5.22)
Z przyrównania modułów w wyrażeniu (5.22) znajdujemy
U   L I  X LI
I
reaktancja indukcyjna
a z przyrównania argumentów
Pomnożenie wskazu I przez
jL powoduje wydłużenie
wskazu I i jego obrót o 90o
„w przód” (rys.5.4)
 u i 
1
U  BLU
L
susceptancja indukcyjna
 u  i 

(5.24)
2
U
=/2
u

I
i
2
Rys.5.4. Wykres wskazowy cewki
-4-
(5.23)
 KONDENSATOR
W punkcie 1.7 stwierdziliśmy, że gdy istnieje napięcie u(t) na
zaciskach idealnego kondensatora o pojemności C, to prąd płynący przez
kondensator opisuje zależność (1.19)
it   C
d u t 
dt
Przyjmując, że na zaciskach kondensatora występuje napięcie
u t   U m sin  t u 
(5.25)
to prąd płynący przez kondensator wynosi


it    C U m sin  t u    I m sin  t i 
2

(5.26)
Z powyższej zależności wynika, że amplituda przebiegu prądu
Im  C U m
natomiast faza początkowa
 i  u 
(5.27)

(5.28)
2
Zatem przesunięcie fazowe  między przebiegami u(t) i i(t)
kondensatora wynosi (rys.5.5):
 u i  

2
u(t), i(t)
i
u
0
(5.29)
Prąd płynący przez
idealny kondensator
wyprzedza napięcie
o 90o
t
/2
Rys.5.5
-5-
Dla kondensatora - symboliczna wartość chwilowa napięcia
gdzie U m  U m e ji
(5.30)
d u t 
 j C U m e jt  I m e jt
dt
(5.31)
u(t )  U m e jt
prądu
it   C
Zatem
I m  j C U m
(5.32)
co oznacza, że
I  j C U
U
Przedstawiając symboliczne
wykładniczej, otrzymujemy
1
I
j C
wartości
I e j i   C U
(5.33)
skuteczne
w


j  u  
2
e 
postaci
(5.34)
Z przyrównania modułów w wyrażeniu (5.34) znajdujemy
I   C U  BC U
U
susceptancja pojemnościowa
a z przyrównania argumentów
Pomnożenie wskazu I przez
1/jC powoduje wydłużenie
wskazu I i jego obrót o 90o
„wstecz” (rys.5.6)
 u i  
2

(5.36)
2
=-/2
i

(5.35)
reaktancja pojemnościowa
 i  u 
I
1
I  XC I
C
U
u
Rys.5.6. Wykres wskazowy kondensatora
-6-
5.2. PODSTAWOWE PRAWA W POSTACI ZESPOLONEJ
Prawo Ohma
Symboliczna wartość skuteczna napięcia U dwójnika
równa się iloczynowi impedancji dwójnika Z i wartości
skutecznej prądu I w nim płynącego:
U ZI
(5.37)
Impedancja (opór zespolony) Z charakteryzuje przewodnictwo
elektryczne dwójnika przy przepływie prądu sinusoidalnego.
Podstawiając w (5.37) symboliczne wartości skuteczne w postaci
wykładniczej, otrzymujemy
czyli:
Zatem
U U e ju U j u i 
Z 
 e
j i
I
I
Ie
(5.38)
U
, arg Z  u i   
I
(5.39)
Z  Z e j
(5.40)
Z
Z R jX
rezystancja
reaktancja
Im
Impedancję
Z
można
przedstawić geometrycznie
na płaszczyźnie zmiennej
zespolonej (rys.5.7) za
pomocą
trójkąta
impedancji.
Z
X

Re
R
Rys.5.7.
-7-
Prawo Ohma można także przedstawić następująco:
Symboliczna wartość skuteczna prądu I płynącego
przez dwójnik równa się iloczynowi admitancji dwójnika
Y i wartości skutecznej napięcia U na jego zaciskach:
I YU
(5.41)
Admitancja (przewodność zespolona – jej jednostką jest simens S)
dwójnika równa się odwrotności jego impedancji:
Y
1
Z
1

(5.42)
co oznacza, że
Y
czyli:
Zatem
Y
Ze
j
1  j
e
Z
(5.43)
1 I
 , arg Y  
Z U
Y  Y e  j
(5.44)
Y G jB
konduktancja
(5.45)
susceptancja
Im
Admitancję
Y
można
przedstawić geometrycznie
na płaszczyźnie zmiennej
zespolonej
(rys.5.8)
za
pomocą trójkąta admitancji.
Y
B
-
Re
G
Rys.5.8.
-8-
I prawo Kirchhoffa - prądowe prawo Kirchhoffa (PPK)
Algebraiczna suma symbolicznych wartości chwilowych
prądów in(t) we wszystkich gałęziach dołączonych do
jednego, dowolnie wybranego węzła obwodu, jest w każdej
chwili czasu równa zeru:
n
  k i k (t )  0
t
(5.46)
k 1
gdzie: k = 1 („+” jeśli prąd elektryczny ma zwrot do węzła; „-” jeśli zwrot
jest przeciwny, od węzła)
Jest ono także słuszne dla symbolicznych amplitud (5.46a) oraz
symbolicznych wartości skutecznych (5.46b) odpowiednich prądów:
n
 k I m k  0
n
(5.46a)
k 1
 k I k  0
(5.46b)
k 1
II prawo Kirchhoffa - napięciowe prawo Kirchhoffa (NPK)
Algebraiczna suma symbolicznych wartości chwilowych
napięć un(t) na wszystkich elementach, tworzących
dowolnie wybrane oczko obwodu jest w każdej chwili
czasu równa zeru:
n
   k u k (t )  0
t
(5.47)
k 1
gdzie: k = 1 („+” jeśli zwrot napięcia jest zgodny z przyjętym za dodatni
kierunkiem obiegu oczka; „-” jeśli jest przeciwny)
Jest ono także słuszne dla symbolicznych amplitud (5.47a) oraz
symbolicznych wartości skutecznych (5.47b) odpowiednich napięć:
n
 kU m k  0
n
(5.47a)
k 1
 kU k  0
k 1
-9-
(5.47b)
5.3. POŁĄCZENIA DWÓJNIKÓW
 Połączenie szeregowe n dwójników (rys.5.9)
Rys. 5.9.
U  U 1  U 2    U n  Z1 I  Z 2 I    Z n I 
n
Zk I  Z I
(5.48)
k 1
Z
n
Zk
(5.49)
k 1
 Połączenie równoległe n dwójników (rys.5.10)
Rys. 5.10.
I  I1  I 2    I n  Y1U  Y 2 U    Y n U 
n
Y k U  Y U
(5.50)
k 1
Y
n
Y k
n
lub
k 1
- 10 -

1
1

Z k 1 Z k
(5.51)
5.4. POŁĄCZENIA ELEMENTÓW R, L, C
Obwód szeregowy RLC
Rysunek 5.11. przedstawia połączenie szeregowe idealnego rezystora
R, idealnej cewki indukcyjnej L i idealnego kondensatora C.
R
L
C
Rys. 5.11.
Wartość
napięcia na elemencie
impedancji elementu
R
UR  RI
ZR  R
L
U L  j L I  jX L I
Z L  j L  j X L
C
UC 
1
1
I j
I   jX C I
j C
C
ZC   j
1
  j XC
C
Ponieważ

U  Z I  R 


1 
 I  R  j  X L  X C  I  R  jX I
j L 

C


(5.52)
Zatem:
2

1 
  R 2   X L  X C 2  R 2  X 2
Z  R 2   L 
C 

(5.53)
1 

L 


C
  arctg  X L  X C   arctg  X 
arg Z    arctg 


R
R
R






(5.54)
- 11 -
Obwód równoległy RLC
R
L
(Rys. 5.12)
C
Rys. 5.12.
Wartość
prądu w elemencie
admitancji elementu
I R  GU
YR G
R
L
IL 
1
j L
U j
1
U   j BL U
L
1
1
  j BL   j
L
XL
Y C  j C  j BC  j
I C  j C U  j BC U
C
YL j
1
XC
Ponieważ

I  Y U  G 


1 
 U  G  j BC  BL  U  G  jB U (5.56)
j C 

L


Zatem:
2

1 
  G 2  BC  BL 2  G 2  B 2
Y  G   C 
L

(5.57)
1 

 C 


L
  arctg  BC  BL   arctg  B 
arg Y  arctg 


G
G
 G 




(5.58)
2
- 12 -
5.5. TWIERDZENIE THEVENINA I NORTONA W POSTACI
SYMBOLICZNEJ
Twierdzenie Thevenina
(o zastępczym źródle/generatorze napięciowym)
Dowolny aktywny dwójnik klasy SLS można zastąpić
obwodem równoważnym, złożonym z szeregowego
połączenia idealnego źródła napięcia (rys.5.13) o napięciu
źródłowym U0 i impedancji wewnętrznej ZW, przy czym:
- napięcie źródłowe U0 jest równe napięciu na rozwartych
zaciskach dwójnika (napięciu stanu jałowego USJ)
- impedancja wewnętrzna ZW, jest równa impedancji
zastępczej (impedancji wejściowej ZAB) dwójnika
pasywnego
(bezźródłowego),
otrzymanego
po
wyzerowaniu w wewnętrznej strukturze dwójnika
aktywnego wszystkich autonomicznych źródeł energii
(zastąpieniu idealnych źródeł napięcia zwarciami, a
idealnych źródeł prądowych rozwarciami).
Wyznaczenie:
oraz
A
A
A
DA
B
DA
A
B
DP
B
B
Rys.5.13
- 13 -
Twierdzenie Nortona
(o zastępczym źródle/generatorze prądowym)
Dowolny aktywny dwójnik klasy SLS można zastąpić
obwodem równoważnym, złożonym z równoległego
połączenia idealnego źródła prądu (rys.5.14.) o prądzie
źródłowym IZ i admitancji wewnętrznej YW, przy czym:
- prąd źródłowy IZ jest równy prądowi płynącemu przez
zwarte zaciski dwójnika (prądowi stanu zwarcia ISZ)
- admitancja wewnętrzna YW, jest równa admitancji
zastępczej (admitancji wejściowej YAB) dwójnika
pasywnego
(bezźródłowego),
otrzymanego
po
wyzerowaniu w wewnętrznej strukturze dwójnika
aktywnego wszystkich autonomicznych źródeł energii
(zastąpieniu idealnych źródeł napięcia zwarciami, a
idealnych źródeł prądowych rozwarciami).
Wyznaczenie:
oraz
A
A
A
DA
B
DA
A
B
DP
B
B
Rys.5.14
- 14 -
5.6. MOC W OBWODACH PRĄDU HARMONICZNEGO
Jeśli na zaciskach układu klasy SLS występuje wymuszenie
harmoniczne napięciowe, to prąd zmienia się również sinusoidalnie z tą
samą pulsacją:
u t   U m sin  t u 
it   I m sin  t i 
Moc chwilowa pobierana przez analizowany układ wyniesie zatem
pt   u t it   U m sin  t u  I m sin  t i 
(5.59)
Na
podstawie
tożsamości
2 sin  sin   cos     cos    ,
powyższą zależność zapiszemy w postaci
pt  
UmIm
U I
cosu i   m m cos2 t u i 
2
2
UmIm Um Im

U I
2
2 2
a ponieważ
oraz
(5.60)
 u i
ostatecznie otrzymamy (rys.5.15)
pt   U I cos   U I cos2 t u i 
(5.61)
p(t)
p(t)
1
u(t)
i(t)
t
t
2
- 15 -
rys.5.15
Wartość średnią mocy p(t) można określić, uwzględniając jej
okresowość, jako:
1
Psr 
T
t 0 T
 pt dt
t0
(5.62)
Tę wartość średnią w obwodach prądu harmonicznego nazywamy
MOCĄ CZYNNĄ i oznaczamy przez P
P  U I cos 
[W]
(5.63)
W obwodach prądu harmonicznego iloczyn wartości skutecznych napięcia
i prądu nazywamy
MOCĄ POZORNĄ i oznaczamy przez S
S UI
[VA]
(5.64)
Istnieje ponadto pojęcie
MOCY BIERNEJ oznaczanej symbolem Q
Q  S2  P2 
UI 2  UI cos 2  UI
1  cos 2   UI sin  [var]
(5.65)
- 16 -
ZESPOLONĄ MOCĄ POZORNĄ nazywamy wielkość
S U I*
(5.66)
Podstawiając U  U e j u oraz I *  I e  j i otrzymujemy
S  U I e j  u  i   U I e j  U I cos   j sin  
(5.67)
Część rzeczywista zespolonej mocy pozornej jest równa mocy czynnej P, a
część urojona mocy biernej Q układu, czyli:
P  U I cos   Re S 





Q  U I sin   Im S 
(5.68)
Wobec tego zespoloną moc pozorną można przedstawić w postaci:
S  P  jQ
(5.67)
Moduł zespolonej mocy pozornej
S  P2  Q2  U I
(5.68)
jest równy mocy pozornej układu
a argument zespolonej mocy pozornej
arg S  
(5.69)
kątowi przesunięcia fazowego między napięciem i prądem
Im
Zespoloną moc pozorną S
można
przedstawić
geometrycznie na płaszczyźnie
zmiennej zespolonej (rys.5.16)
za pomocą trójkąta mocy.
S

P
- 17 -
Q
Re
Rys.5.16.
Wyrazimy zespoloną moc pozorną
impedancji Z dwójnika.
Na podstawie prawa Ohma mamy:
w
zależności
od
U ZI
S U I*  Z I I*
czyli
S  Z I 2  R  j X  I 2
wobec czego
(5.70)
Moc czynna i bierna wynoszą zatem
P  Re S   R I 2 , Q  Im S   X I 2
(5.71)
a moc pozorna jest równa
S  P2  Q2  Z I 2
Natomiast zespolona moc pozorna
admitancji Y dwójnika.
Na podstawie prawa Ohma mamy:
(5.72)
w
zależności
od
I YU
Wartość sprzężoną I* otrzymamy, zastępując wszystkie wielkości
występujące w tym wzorze przez wielkości sprzężone.
S  U I *  U Y *U *
Zatem
S  Y *U 2  G  j B U 2
wobec czego
(5.73)
Moc czynna i bierna wynoszą zatem
P  Re S   G U 2 , Q  Im S    B U 2
(5.74)
a moc pozorna jest równa
S  P 2  Q 2  YU 2
- 18 -
(5.75)
DOPASOWANIE OBCIĄŻENIA DO ŹRÓDŁA
Mówiąc o dopasowaniu, mamy najczęściej na myśli warunek
uzyskania maksymalnej mocy czynnej użytecznej.
A
B
Dwójnik źródłowy z impedancją obciążenia
Impedancja obciążenia ma postać:
Z  Ze J  R  jX
(5.76)

lub jako admitancja:
Y  Ye  j  G  jB
(5.77)

Moc czynną wydzieloną na obciążeniu określają relacje


P  Re U  I   R I  G U
2
2
(5.78)
Dokonajmy przekształceń ostatniego równania:
P  RI
2
U0
R
2
Z Z
W
= U0
2
R
U0
2
( RW  R )  j ( X W  X )
2


R
2
( RW  R)  ( X W  X )
P  f ( R, X )
- 19 -
2
(5.79)
(5.80)
Moc użyteczna jest więc funkcją dwóch parametrów obciążenia: R i X.
Wyznaczmy pochodne cząstkowe:
RW  R 2  ( X W  X )2
P
2
 U0
R
( RW  R)2  ( X W  X )2
2


2 R( X W  X )
P
2
  U0
X
( RW  R)2  ( X W  X )2

2
(5.81)

2
Funkcja (5.80) ma ekstremum (max) w punkcie, dla którego jest
spełniony układ równań:
P
P
0;
0
R
X
(5.82)
co sprowadza się do warunku:
RW  R2  ( XW  X )2  0 ; XW  X  0
2
(5.83)
Warunek dopasowania ze względu ma maksymalną moc czynną ma więc
postać:
R  RW
;
X  XW ;
Z Z

;
G  GW
B   BW
Y Y
(5.84)

Impedancja (admitancja) obciążenia musi być równa impedancji
(admitancji) sprzężonej do impedancji (admitancji) źródła.
W takim przypadku w obciążeniu wydziela się maksymalna moc czynna
oraz przesyłania mocy przy dopasowaniu wyniosą:
Pmax 
U0
2
4 RW
u  i 
- 20 -
P
1

P  PW 2
(5.85-6)