M c

Poszukiwanie cząstek
Ciemnej Materii przy użyciu
dwufazowego detektora
argonowego
Piotr Mijakowski
Seminarium Doktoranckie IPJ, Warszawa, 25 Październik 2005
Plan wystąpienia
• Ciemna Materia
• Zasady detekcji bezpośredniej
• Dwufazowy detektor argonowy
– Zasada działania (WARP, ArDM)
– Sposoby eliminacji tła doświadczalnego
• Symulacja oddziaływań neutronów
przy użyciu Geant4
2
Pierwsze dowody na istnienie
Ciemnej Materii
Zwicky
Problem „brakującej masy”
- 1933 r. - Fritz Zwicky, gromada COMA.
Prędkość obrotu galaktyk wokół wspólnego
środka masy zbyt duża aby mogły one
tworzyć układ związany.
gromada COMA
Rozwiązanie
ok. 90% masy „niewidoczna”
3
Pomiar krzywych rotacji galaktyk
V~r
V~r-1/2
sferyczne halo ciemnej materii
otaczające galaktykę
4
Pomiar gęstości materii we
Wszechświecie - kolejne dowody
równania ewolucji Wszechświata
gęstość krytyczna : rc = 3H2/8pG (Wm = r/rc)
W = Wm+WL
Większość materii we Wszechświecie to ciemna materia!
 Pomiar promieniowania gwiazd i materii międzygwiezdnej
=> materia „świetlista”
Wlumni ~ 0.006
 Pomiar oddziaływań grawitacyjnych (np. rotacja galaktyk)
=> materia „grawitacyjna”
Wm ~ 0.3
 Pomiar promieniowania mikrofalowego tła (WMAP – 2003 r.)
Wm = 0.29  0.07
„płaski”
Wszechświat !
Wtot = 1.02  0.02
5
Pomiar gęstości materii we
Wszechświecie
Większość ciemnej materii to materia niebarionowa!
 Model nukleosyntezy
Wb = 0.040  0.005
 Promieniowanie mikrofalowe tła
Wb = 0.047  0.006
Wnioski:
Wm>> Wb => Ciemna Materia
Wm<<1 => Ciemna Energia
6
Ciemna materia - klasyfikacja
~ 4%
Klasyfikacja Ciemnej Materii
• Barionowa Ciemna Materia - np. brązowe karły, gwiazdy neutronowe,
czarne dziury - MACHO’s (Massive Astronomical Compact Halo Objects)
• Niebarionowa Ciemna Materia
– „gorąca” (Hot Dark Matter - HDM), cząstki relatywistyczne,
np. neutrina
~ 23% – „zimna” (Cold Dark Matter - CDM), cząstki nie-relatywistyczne,
np. WIMP-y (Weakly Interacting Massive Particles) - wolne,
masywne, neutralne cząstki , słabo oddziałujące z materią
„zimna” czy „gorąca”?
CDM
bottom-up
HDM
top-down
7
WIMP kandydat na
„Zimną” Ciemną Materię
Słabo Oddziaływująca Masywna Cząstka
(WIMP – Weakly Interacting Massive Particle)
Poszukujemy cząstek:




Neutralnych
Długożyciowych (z t ~ czas życia Wszechświata)
Masywnych ( Mc ~ 100 GeV)
Słabo odziałujących z materią
dobry kandydat na WIMP-a:
neutralino c (SUSY)
- najlżejsza cząstka supersymetryczna LSP (Lightest
Supersymmetric Particle), jest stabilna
neutralino(c)
18 GeV < Mc < 7 TeV
8
Metoda detekcji bezpośredniej
c + (A,Z)w spoczynku  c + (A,Z)odrzut
Jądro
odrzutu
Todrzutu~ keV
detektor
mierzymy energię jąder odrzutu
z elastycznego rozpraszania
WIMP-ów
9
Energia odrzutu
+
=
model halo
widmo energii jąder
odrzutu z
oddziaływania
WIMP-ów
(symulacja)
• prędkość WIMP-ów w halo: rozkład
Maxwella-Bolzmanna ze średnią prędkością
względem centrum Galaktyki = 0
• Vc  230 km/s (względem Ziemi) -> określa
śred. Tc
• r – gęstość WIMP-ów w halo galaktycznym
(~ 0.3 GeV/c2 ·1/cm3)
Ar
Mc = 50 GeV/c2
<Todrzutu> = 14 keV
Mc = 100 GeV/c2
<Todrzutu> = 24 keV
10
Techniki detekcji sygnału
Ge, Si: CDMS, EDELWEISS
ciepło
jonizacja
Półprzewodniki: Ge, Si
TPC: DRIFT
Detektory kriogeniczne
CRESST, Rosebud Al2O3
ENERGIA
ODRZUTU
LXe+GXe: Zeplin II, XENON
LAr+GAr: WARP, ARDM
CaWO4: CRESST, ROSEBUD
scyntylacja
NaI, CsI, CaF, LXe
DAMA, NAIAD, ZEPLIN I
11
Częstość zdarzeń. Efekt modulacji sezonowej
Liczba rejestrowanych przypadków (Rate):
R ~ r ·V·s
r – gęstość WIMP-ów w halo galaktycznym
d = 30o
s – elastyczny przekrój czynny zależny
od rodzaju sprzężenia WIMP-nukleon,
czynnika postaci F(q2) ... SUSY
V – średnia prędkość
cząstki WIMP względem
nukleonu (tarczy) – ZALEŻY
OD PORY ROKU!
VZiemia =
30 km/s
Sumaryczna prędkość Ziemi i Słońca
względem centrum galaktyki:
Maksimum – 2 czerwiec - V  248 km/h
Minimum – 2 grudzień - V  219 km/h
12
Aktualne limity doświadczalne
•
DAMA NaI,
obszar 90% CL
•
•
DAMA 107731 kg•d
(7 lat, 100 kg NaI)
Inne eksperymenty - nie
stwierdzono przypadków
oddziaływania Ciemnej
Materii; Np. CDMS:
19.4 kg•d (52.6 dni, 1kg
Ge, 0.2 kg Si)
Wartości powyżej linii są
wykluczane na poziomie
ufności 3s
Edelweiss
(Ge)
CDMS II
2004 (Ge)
SUSY
XENON (100kg)
przewidywanie
13
Przewidywania dla projektu ArDM
(Argon Dark Matter)
DAMA NaI,
obszar 90% CL
Założenie: próg
energetyczny detektora
ArDM = 30 keV
≈ 100 przyp. / ton / dzień
przy
Mc = 100 GeV/c2
≈ 1 przyp. / ton / dzień
dla s = 10-46:
≈ 1 przyp. / ton / 100 dni
14
Wymagania dla przyszłych eksperymentów
WYMAGANIA:
• Duża masa detektora (trudne do zrealizowania przy
użyciu detektorów półprzewodnikowych) ->> perspektywa
wykorzystania GAZÓW SZLACHETNYCH: ARGONU,
KSENONU
• Niskie tło eksperymentalne (podziemne laboratoria,
system osłon)
• Skuteczne metody eliminacji przypadków tła w
doświadczeniu (aktywna selekcja przypadków, staranne
symulacje poziomu tła)
15
Tło eksperymentalne – 2 klasy przypadków
n, c
n, c
g,
 Neutrony i WIMPy: taki sam
sygnał !!!
 Głównie niskoenergetyczne
neutrony TN < 10 MeV
(radioaktywność otoczenia i
oddziaływania mionów) ~ 103 dzień
 Wielokrotne rozpraszanie
neutronów w detektorze –
jedyne kryterium
e-
e-
główne źródło tła
w doświadczeniu
~ 106 dzień
Konstrukcja detektora
powinna umożliwiać
eliminację tła 
16
amplituda [jedn. aut.]
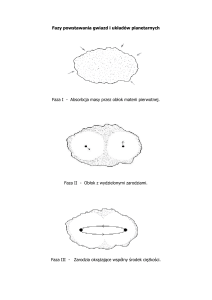
Detektor dwufazowy – zasada działania
neutron
amplituda [mV]
czas dryfu [ms]
elektron
czas dryfu [ms]
17
Detektor dwufazowy – eliminacja tła
symulacja dla detektora LAr - neutrony vs. fotony (ArDM)
próg
g
zliczenia/przedz.
z testów detektora argonowego (WARP)
g, e
a
S2/S1
18
Detektor dwufazowy – przykłady rozwiązań
ArDM
Argon Dark
Matter
WARP
Wimp Argon Programme
LEM
60 cm
300 cm
Ar (10 cm)
170 cm
LAr (120 cm)
100 litrów
~ 700 litrów
fotopowielacze
19
Tło neutronowe
• sygnał z oddziaływania WIMP-ów i neutronów taki sam w detektorze
• redukcja tła neutronowego  większa czułość detektora
SYMULACJE – w jakim celu?
 projekt detektora (wymagania dla system osłon,
aktywnego veta)
 określ. prawd. wielokrotnego rozpraszania
 określ. czułości detektora  analiza danych
z doświadczenia
20
Źródła neutronów
NEUTRONY – źródła
- spontaniczne rozszczepienie 238U
- reakcje (a,n); a z szeregów prom. z rozpadów U/Th
- produkcja przez miony kosmiczne
ze skały
z mionów
strumień [cm-2s-1keV-1 ]
liczba neutronów , MeV-1, mion-1
z elementów det.
energia
neutronów [keV]
energia neutronów [MeV]
21
Symulacja Geant4 dla projektu ArDM
I etap
(monoenergetyczne neutrony)
 oddziaływanie neutronów w LAr
 TN < 20 MeV
 analiza procesów: wychwyt neutronu, elastyczne
rozpraszanie
II etap
(rozkłady energii początkowej neutronów)
 oddziaływanie neutronów tła w cylindrze z LAr
 widma energii odrzutu
 prawd: wielokrotnego rozpraszania, oddziaływania,
wychwytu
 droga pomiędzy oddziaływaniami
22
Wychwyt neutronów w LAr
Rozkład energii fotonów z wychwytu neutronów w LAr
(argon naturalny: 40Ar - 99,6%, 36Ar - 0.337%, 38Ar - 0.063%)
Energia początkowa neutronów = 10 eV
Średnia liczba g
powstających
w wychwycie = 3.5
23
Rozpraszanie elastyczne neutronów w LAr
Widmo energii jąder
odrzutu 40Ar
dla TN = 2 MeV
Tn<<Mn
nierelat.
dN Ar
ds
ds
~ d (cos  
 dTAr 
d (cos 
d (cos 
2


2
2


m
2  M Ar  mn
M

2
n
Ar
 cos  +
 
TAr = Tn 1 
+
sin


(
M

m
)

T
 (1  cos )

Ar
n
n
2 
2
2

m
(

(

m
+
M
m
+
M
n
n
Ar
n
Ar


 


24
Neutrony ze skały – przykład analizy
Widmo energii jąder
odrzutu
Rozkład energii
początkowej
geometria
h=120 cm
Fn = 3.8•10-6 n/s·cm2
r=40 cm
całkowity strumień neutronów
ze skały
(dane z lab. Canfranc)
13200 wchodzących
neutronów na dzień !!!
10 keV threshold
550 neutronów na godzinę
1 neutron co ~ 6.5 sec.
25
Neutrony ze skały
– przykład analizy
liczba niezident.
neutronów
Poddział. ~57 %
13200
n / dzień
7500
n / dzień
Pwielokrot.~53%
7500 – 4000
= 3500
prawd. wiel. oddz. dla
n / dzień
oddz. neutronów
rozdzielczość 2 cm
 rejestracja 97%
wiel. oddziaływań
3600
n / dzień
dodanie moderatora:
zmniejszenie
strumienia 106 razy
1 n / rok
26
Podsumowanie
 Ciemna Materia (23%), Ciemna Energia (73%) jedna z
największych zagadek astrofizyki oraz fizyki cząstek
elementarnych
 Próby rejestracji oddziaływań cząstek Ciemnej Materii 
wiele projektów, perspektywy wykorzystania gazów
szlachetnych (dwufazowe detektory argonowe,
ksenonowe)
 Tło eksperymentalne  znacząco obniża czułość detektora
 Jednym z realizowanych projektów jest eksperyment
ArDM:
- projekt detektora (CAD)
- testy – pomiar światła (PMT), ładunku (LEM), HV
- symulacje – tło doświadczalne, odczyt sygnału
27
BACKUP
Pomiary gęstości materii we
Wszechświecie - kolejne dowody
Einstein -> równania ewolucji
Wszechświata
W = Wm+WL
gęstość krytyczna : rc = 3H2/8pG (Wm = r/rc)
W<1
Większość materii we Wszechświecie to
ciemna materia!
 Pomiar promieniowania gwiazd i materii
międzygwiezdnej => materia „świetlista”
W=1
Wlumni ~ 0.006
 Pomiar oddziaływań grawitacyjnych (np.
rotacja galaktyk) => materia „grawitacyjna”
W>1
Wm ~ 0.3
 Pomiar promieniowania mikrofalowego tła
(WMAP – 2003 r.)
„płaski”
Wszechświat !!!
Wtot = 1.02  0.02
Wm = 0.29  0.07
29
CDM vs. HDM
Symulacja ewolucji
struktur materii
Teleskop Hubble’a
CDM za dużo małych
struktur?
HDM problem
z tworzeniem
niewielkich struktur
30
WIMP-y a teoria Superstrun (SUSY)
• Teoria rozwiązuje tzw. problem hierarchii: dlaczego MPlanck >> ME-S ? Dlaczego masy cząstek są tak
niewielkie w porównaniu do masy Plancka? Rozwiązanie polega na wprowadzeniu zestawu masywnych
cząstek w ten sposób, że każdej cząstce elementarnej z Modelu Standardowego odpowiada pewien
supersymetryczny partner. Fermionom odpowiadają supersymetryczne bozony, nośnikom siły – bozonom –
sfermiony.
• Teoria wprowadza nową wielkość kwantową, tzw. parzystość R
(R=+1 dla cząstek MS oraz –1 dla cząstek supersymetrycznych).
Parzystość R jest multiplikatywną liczbą kwantową, jej zachowanie
ma daleko idące konsekwencje:
- proton jest stabilny
- cząstki SUSY produkowane/annihilują zawsze w parach
- rozpadają się na nieparzystą liczbę cząstek SUSY
- najlżejsza cząstka supersymetryczna LSP (Lightest Supersymmetric
Particle) jest stabilna – zachowuje się jak ciężkie neutrino.
neutralino (c)
aktualne limity na masę neutralina (LEP): 18 GeV <
Mc
< 10 TeV
31
32
DAMA NaI (~100kg)
DArk MAtter
• Laboratorium Gran Sasso we
Włoszech (4000 mwe)
• 1996 – lipiec 2002 (7 cykli
zbierania danych)
• Detekcja oparta na
kryształach NaI - 10 x 9.7 kg
100 kg; sygnał rejestrowany
w każdym z detektorów
przez dwa fotopowielacze.
Problem z odróżnieniem tła.
• Energie > 2 keV
• Ekspozycja - 107731 kg•dni
• LIBRA ( ~250 kg) – działa od
marca 2003
33
DAMA – sezonowa modulacja sygnału.
Odkrycie ciemnej materii?
Charakterystyki sygnału






cos(t)
okres jednego roku
faza – lato/zima
niskie energie
amplituda  7%
sygnał w jednym detektorze
„Jaki inny efekt fizyczny spełnia
wszystkie 6 kryteriów?”
dopasowanie Acos[w(t-t0)]
A = (0.0200  0.0032) cpd/kg/keV
t0 = (140  22) day
T = (1.00  0.01) year
Źródło: astro-ph/0311046, 3 Listopad 2003
34
CDMS (Cryogenic Dark Matter Search)
• CDMS II Stanford (20012002);
głęb. 10 m (17 mwe)
• CDMS II Soudan Lab (20032005);
głęb. 713 m (2090 mwe);
redukcja tła neutronowego
z ~1/kg/dzień do ~1/kg/rok
• Detektory Ge (każdy 250g)
oraz Si (100g)
Dwa niezależne pomiary
energii odrzutu: jonizacja,
fonony
• Energie 10-100 keV
(DAMA > 2 keV)
T < 0.01 K
35
CDMS
Wieża 1
ZIP (Z-dependent
Ionization and
Phonon) detector
6 detektorów ZIP
3xGe,Si,Ge,Si
(1kg Ge, 0.2kg Si)
grubość – 1 cm
średnica 7,5 cm
36
CDMS II – wyniki (Soudan Lab)
Kalibracja
3 maj
2004
Wyniki (19.4 kg•d)
• „Ionization yield” (stosunek energii z jonizacji do energii z
fononów) zależy silnie od typu rozpraszania
• Większość cząstek tła (elektrony, gammy) rozprasza się na
elektronach
• WIMP-y oraz neutrony oddziałują z nukleonami
37
3 maj
2004
CDMS II – wyniki (Soudan Lab)
CDMS II (Stanford)
DAMA NaI,
obszar 90% CL
• Nie stwierdzono
przypadku
oddziaływania z ciemną
materią; ekspozycja
19.4 kg•d (52.6 dni, 1kg
Ge, 0.2 kg Si)
• Wartości powyżej
zaznaczonego limitu są
wykluczone na poziomie
ufności 3s
Edelweiss
CDMS II
(2004)
38
Metoda detekcji pośredniej
rc
c
Ziemia
Słońce
sscatt
nm
n int.
m int.
Gcapture
Gannihilation
qq
cc 
ll
W  , Z, H
 .....  n m
detektor
m
 cc , bb , tt ,t +t  , Z 0 , H 0
39
Argon vs Ksenon
40