Oznaczanie ciepła spalania paliw gazowych

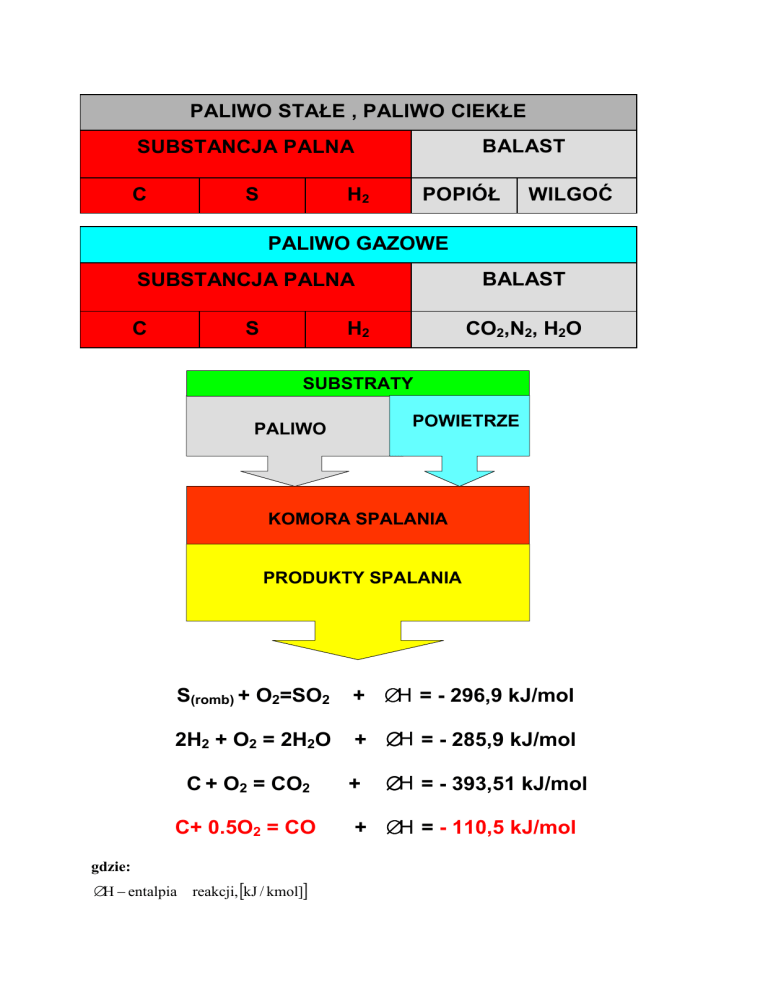
PALIWO STAŁE , PALIWO CIEKŁE
BALAST
SUBSTANCJA PALNA
C
S
POPIÓŁ
H2
WILGOĆ
PALIWO GAZOWE
BALAST
SUBSTANCJA PALNA
C
S
CO2,N2, H2O
H2
SUBSTRATY
POWIETRZE
PALIWO
KOMORA SPALANIA
PRODUKTY SPALANIA
S(romb) + O2=SO2
+ ∆H = - 296,9 kJ/mol
2H2 + O2 = 2H2O
+ ∆H = - 285,9 kJ/mol
C + O2 = CO2
C+ 0.5O2 = CO
gdzie:
∆H − entalpia reakcji, [kJ / kmol]]
+
∆H = - 393,51 kJ/mol
+ ∆H = - 110,5 kJ/mol
Spalanie zupełne – jeżeli w spalinach nie ma palnych części gazowych (np. CO, CxHy).
Spalanie całkowite – jeżeli w produktach spalania nie ma palnych części stałych (np. sadza,
koksik lotny i in.).
Współczynnik nadmiaru powietrza λ :
λ=
na
n a min
n a , n a min – rzeczywista ilość powietrza doprowadzonego do spalania, teoretyczna ilość
powietrza niezbędna do spalenia zupełnego i całkowitego paliwa [kmol/j.p].
j.p – jednostka ilości paliwa: w przypadku paliw stałych i ciekłych j.p=kg paliwa wilgotnego
lub dla paliw gazowych j.p=kmol gazu suchego.
Kontrakcja chemiczna ∆Vch – różnica objętości substratów i wilgotnych produktów
spalania.
Kontrakcja fizyczna ∆Vf – różnica objętości substratów i produktów po uwzględnieniu
wykroplenia się pary wodnej.
Kontrakcja całkowita ∆V=∆
∆Vf+∆
∆Vch – suma kontrakcji chemicznej i fizycznej.
Wartość opałowa – Qi jest to ilość ciepła, jaka powstaje w wyniku spalania zupełnego
i całkowitego jednostki ilości paliwa przy założeniu, że produkty spalania zostaną ochłodzone
do temperatury substratów, a para wodna zawarta w spalinach nie ulega wykropleniu.
Ciepło spalania – Qs jest to ilość ciepła, jaka powstaje w wyniku spalania zupełnego
i całkowitego jednostki ilości paliwa przy założeniu, że para wodna zawarta w spalinach
ulegnie całkowitemu wykropleniu.
Q i = Q s − m′′ ⋅ r
m′′ – masa skroplin uzyskana ze spalenia jednostki ilości paliwa: dla paliw stałych i
ciekłych [kg/kg], dla paliw gazowych [kg/um3]
r
– entalpia skraplania pary, [kJ/kg]
Paliwa ciekłe i stałe: Qi [kJ/kg], Qs [kJ/kg],
Paliwa gazowe:
Qi [kJ/um3], Qs [kJ/um3].
1 um³ (umowny metr sześcienny) jest to ilość substancji zawartej w 1 m³ gazu doskonałego
lub półdoskonałego o ściśle określonym ciśnieniu pN i temperaturze TN. Parametry pN, TN
nazywamy parametrami umownymi.
Najczęściej przyjmuje się następujące wartości parametrów umownych: pN = 1 bar,
TN = 273,15 K, które nazywa się parametrami umownymi SI.
Bilans energetyczny kalorymetru Junkersa
E& d = E& w + ∆E& u
E& d
– strumień energii doprowadzonej do układu,
E& w – strumień energii wyprowadzonej z układu,
∆E& u = E& u 2 − E& u1 , to przyrost strumienia energii układu.
&
Gaz: &Ig , E& kg , E& pg , Q
Spaliny: E& ks , E& ps , &Is
.
Woda chłodząca: &I w1
Woda chłodząca: &I w 2
Powietrze:
&I , E& , E&
p
kp pp
Straty ciepła do
&
otoczenia: Q
str
gdzie:
&I
g
–
strumień entalpii spalanego gazu,
&I
p
–
strumień entalpii powietrza doprowadzanego do procesu spalania,
&I
w1
–
strumień entalpii wody chłodzącej, dopływającej do kalorymetru Junkersa,
E& kg
–
strumień energii kinetycznej spalanego gazu,
E& kp
–
strumień energii kinetycznej powietrza doprowadzanego do procesu spalania,
E& pg
–
strumień energii potencjalnej spalanego gazu,
E& pp
–
strumień energii potencjalnej powietrza doprowadzanego do procesu spalania,
&
Q
–
strumień ciepła wydzielonego w wyniku spalania gazu,
&I
s
–
strumień entalpii spalin,
E& ks
–
strumień energii kinetycznej spalin,
E& ps
–
strumień energii potencjalnej spalin,
I& w 2
–
strumień entalpii wody chłodzącej, wypływającej z kalorymetru Junkersa,
&
Q
str
–
strumień strat ciepła do otoczenia.
Pomiar powinien być przeprowadzony w stanie ustalonym, wtedy ∆E& u = 0
Warunki, które powinny być spełnione, aby kalorymetr Junkersa znajdował się w stanie
ustalonym są następujące:
•
stałe natężenie przepływu: gazu, powietrza, wody chłodzącej oraz spalin,
•
stałe ciśnienie gazu, otoczenia,
•
stały rozkład temperatury.
Aby zminimalizować straty ciepła przez konwekcję oraz promieniowanie powinny być
dodatkowo spełnione następujące warunki:
•
•
∆t w między temperaturą wody wypływającej t w 2
i dopływającej t w1 z /do kalorymetru Junkersa powinna mieścić się w przedziale
∆t w = t w 2 − t w1 = 6 ÷ 10K
średnia arytmetyczna temperatura wody chłodzącej kalorymetr t w powinna być równa
różnica
temperatury
temperaturze otoczenia t w = 0,5(t w2 + t w1 ) = t ot .
Jeżeli kalorymetr Junkersa znajduje się wstanie ustalonym, to przyrost strumienia energii
układu ∆E& u = E& u2 − E& u1 = 0 , czyli strumień energii układu pozostaje niezmienny E& u 2 = E& u1 ,
zatem: E& d = E& w
Strumień energii dopływającej do układu E& d :
& + &I + E& + E& + &I
E& d = &Ig + E& kg + E& pg + Q
p
kp
pp
w1
Strumień energii wypływającej z układu E& w :
&
E& w = &I s + E& ks + E& ps + &I w2 + Q
str
Wobec tego, że w stanie ustalonym spełnione jest równanie E& d = E& w zatem:
& + I& + E& + E& + &I == &I + E& + E& + &I
&
&I + E& + E& + Q
g
kg
pg
p
kp
pg
w1
s
ks
ps
w 2 + Q str
Założenia upraszczające bilans energetyczny kalorymetru Junkersa:
•
ze względu na bardzo małą prędkość przepływu (v≈0 ): gazu, powietrza oraz spalin,
można pominąć strumienie energii kinetycznej: gazu, powietrza oraz spalin
E& kg , E& kp , E& ks ≈0,
•
ze względu na to, że różnica poziomów ∆h <80-100m, można pominąć strumienie
energii potencjalnej: gazu, powietrza oraz spalin E& pg , E& pp , E& ps ≈0
•
nie ma kontrakcji chemicznej, czyli różnica między objętością substratów oraz
objętością wilgotnych produktów spalania ∆Vch= 0
∆Vch = Vsubstratów − Vwi lg otnych produktów = 0
gdzie:
Vsubstratów = Vg + Vp = Vwi lg otnych produktów = Vs ,
Vg , Vp , Vs − objętość gazu, powietrza, spalin
- jeżeli założymy dodatkowo, że gęstość gazu ( ρ g ), powietrza ( ρ p ), spalin ( ρs ) jest taka
sama:
ρ g ≈ ρ p ≈ ρs
to można zapisać, że suma masy gazu ( m g ) i powietrza ( m p ), czyli substratów jest
w przybliżeniu równa masie spalin ( m s )
mg + m p ≈ ms
- jeżeli założymy, z błędem ±0,5%, że ciepło właściwe gazu c pg , powietrza c pp , spalin
c ps przy stałym ciśnieniu jest w przybliżeniu takie samo:
c pg ≈ c pp ≈ c ps ≈ c p
-
z definicji wartości opałowej wynika, że temperatura gazu (tg), powietrza (tp) i spalin(ts)
jest taka sama
tg = t p = ts = t
wobec tego po obustronnym pomnożeniu równania:
mg + m p ≈ ms
przez iloczyn c p ⋅ t ≈ c pg ⋅ t g ≈ c pp ⋅ t p ≈ ⋅c ps ⋅ t s
uzyskuje się następujące równanie :
m g ⋅ c pg ⋅ t g + m p ⋅ c pp ⋅ t p ≈ m s ⋅ c ps ⋅ t s
które po wykorzystaniu równania definiującego entalpię :
I = m cp t
można zapisać w następującej postaci:
Ig + I p ≈ Is
gdzie:
Ig
–
entalpia gazu,
Ip
–
entalpia powietrza,
Is
–
entalpia spalin,
Posługując się strumieniem entalpii ( &I ), czyli ilorazem entalpii ( I ) i czasu (τ):
&I = I
τ
można napisać, że suma strumieni entalpii gazu ( &I g ) i powietrza ( &I p ) jest równa
strumieniowi entalpii spalin ( &I ) :
s
&I + &I = &I
g
p
s
•
strumień strat ciepła do otoczenia:
&
&
&
Q
str = Q k + Q r = 0
gdzie:
& – strumień ciepła, traconego do otocznia przez konwekcję,
Q
k
&
Q – strumień ciepła, traconego do otocznia przez promieniowanie.
r
& = 0, Q
& = 0 wynika to z konstrukcji kalorymetru Junkersa oraz warunków
Q
k
r
przeprowadzania pomiaru, o czym wspomniano wcześniej:
∆t w = t w 2 − t w1 = 6 ÷ 10K , t w = 0,5( t w 2 + t
w1
) = t ot
Ostatecznie, po wprowadzeniu uproszczeń, bilans energetyczny kalorymetru Junkersa można
zapisać w następującej postaci:
& + &I = &I
Q
w1
w2
lub po przekształceniu
& = &I
&
& w ⋅ c tw 2 ⋅ (t w 2 − t w1 )
Q
w 2 − I w1 = m
tw1
gdzie:
&
Q
– strumień ciepła wydzielonego podczas spalenia określonej ilości gazu,
&I , &I – strumień entalpii wody chłodzącej na dopływie oraz wypływie z kalorymetru
w1 w2
Junkersa,
tw2
c tw1
– średnie ciepło właściwe wody w zakresie temperatur tw1 i tw2. Ponieważ zmiana
temperatury wody jest niewielka, wobec tego można nie uwzględniać wpływu temperatury
wody na wartość ciepła właściwego wody i przyjmować wartość cw=4,19 kJ/kgK.
Strumień wydzielanego ciepła:
& =V
&
Q
gN ⋅ Q s
gdzie :
Qs – ciepło spalania paliwa gazowego,
&
V
gN – strumień spalanego gazu [um³].
Ciepło spalania gazu Qs:
Qs =
&
& ⋅ c ⋅ (t
− t ) m ⋅ c ⋅ (t
−t )
m
Q
= w w w 2 w1 = w w w 2 w1
&
&
VgN
V
V
gN
gN
Wartość opałowa gazu:
Q i = Q s − m ′′ ⋅ r = Q s −
m skr ⋅ r
VgN
gdzie:
m′′ – masa skroplin uzyskana ze spalenia jednostki ilości paliwa gazowego, [kg/um³]
r
– entalpia skraplania pary, [kJ/kg]
m′′ =
m skr ⋅  kg 
,

VgN  um 3 
Ilość spalonego gazu oblicza się ze wzoru:
p N VgN
TN
=
p g Vg
Tg
VgN =
p g ⋅ Vg ⋅ TN
p N ⋅ Tg
, [um³]
Ciśnienie gazu suchego ( p g )
p g = ∆p g + p b − p s
∆p g – nadciśnienie gazu w gazomierzu, [Pa]
pb
– ciśnienie barometryczne, [Pa]
ps
– ciśnienie nasycenia pary wodnej dla temperatury gazu tg , [Pa]
MATERIAŁY PRZYDATNE DO ANALIZY WYNIKÓW POMIARÓW
1. Rozporządzenie Ministra Gospodarki z dnia 2lipca 2010 w sprawie szczegółowych
warunków funkcjonowania systemu gazowego (Dz.U.z 2010r. Nr.133, poz.891).
2. Polskie Normy:
•
•
PN-C-04750: Paliwa gazowe. Klasyfikacja, oznaczenia i wymagania.
PN-C-04753: Gaz ziemny. Jakość gazu dostarczanego odbiorcom z sieci
rozdzielczej.
WZGLĘDNA GĘSTOŚĆ GAZU
Stosunek gęstości danego gazu do gęstości suchego powietrza w tej samej temperaturze i pod
tym samym ciśnieniem.
d=∆=
ρg
ρp
LICZBA WOBBEGO
Liczba Wobbego-Wo, [kJ/um3]: ciepło spalania gazu podzielone przez pierwiastek
kwadratowy ze względnej gęstości gazu odniesionej do powietrza:
Wo =
Qs
d
Wartość liczby Wobbego jest podstawą do podziału paliw gazowych na podgrupy.
System
Wyszczególnienie
Jednostka
gazu
gazu
gazu
ziemnego
ziemnego
ziemnego
grupy E
grupy Lw
grupy Ls
ciepło spalania
MJ/m3
≥ 34,1
≥ 30,1
≥ 26,1
wartość opałowa
MJ/m3
≥ 31,0
≥ 27,0
≥ 24,0
- nominalna
MJ/m3
50,0
41,5
35,0
- zakres zmienności
MJ/m3
45,0-54,0
37,5-45,0
32,5-37,5
zawartość siarkowodoru
mg/m3
≤ 7,0
≤ 7,0
≤ 7,0
zawartość tlenu
% mol/mol
≤ 0,2
≤ 0,2
≤ 0,2
zawartość ditlenku węgla
% mol/mol
≤ 3,0
≤ 3,0
≤ 3,0
µg/m3
≤ 30,0
≤ 30,0
≤ 30,0
ºC
≤ +3,7
≤ +3,7
≤ +3,7
ºC
≤ -5,0
≤ -5,0
≤ -5,0
ºC
0
0
0
mg/m3
≤ 30,0
≤ 30,0
≤ 30,0
mg/m3
≤ 1,0
≤ 1,0
≤ 1,0
mg/m3
≤ 16,0
≤ 16,0
≤ 16,0
mg/m3
≤ 40,0
≤ 40,0
≤ 40,0
górna liczba Wobbego
zawartość par rtęci
temperatura punktu rosy wody
dla 5,5 MPa od 1 kwietnia do
30 września
temperatura punktu rosy wody
dla 5,5 MPa od 1 października
do 31 marca
temperatura punktu rosy
węglowodorów
zawartość węglowodorów
mogących ulec kondensacji
w temp. -5ºC przy ciśnieniu
panującym w gazociągu
zawartość pyłu o średnicy
cząstek większej niż 5 µm
zawartość siarki
merkaptanowej
zawartość siarki całkowitej