Elementy elektrodynamiki oraz
obwody elektryczne prądu stałego
i przemiennego
Dr inż. Andrzej Skiba
Katedra Elektrotechniki Teoretycznej i
Informatyki
Politechniki Gdańskiej
Gdańsk 16 stycznia 2016
Plan wykładu:
1. Rozwiązanie zadania z poprzedniego wykładu
2. Pojemność jako element obwodu elektrycznego
2.1. Definicja pojemności elektrycznej
2.2. Pojemnościowy dzielnik napięciowy
2.3. Siła przyciągania się okładzin kondensatora
2.4. Zależność pomiędzy prądem i napięciem
2.5. Obwody prądu stałego z elementami RC
3. Indukcyjność jako element obwodu elektrycznego
3.1. Definicja indukcyjności
3.2. Zależność pomiędzy prądem i napięciem
4. Obwody z sinusoidalnymi prądami i napięciami
4.1. Prawo Ohma w obwodach prądu przemiennego
4.2. Rozwiązanie obwodu prądu przemiennego
5. Zadania do samodzielnego rozwiązania
1. Rozwiązanie zadanie z poprzedniego
wykładu
Wyznaczyć taką wartość Rx, by moc wydzielająca się w
tej rezystancji była największa z możliwych. Obliczyć
tę maksymalną moc. Obliczyć wszystkie pozostałe
prądy płynące w obwodzie i sprawdzić bilans mocy.
Do rozwiązania zadania wykorzystane zostanie
twierdzenie Thevenina.
Wyodrębniony linią kreskowaną dwójnik aktywny
zastąpiony zostanie źródłem napięciowym o
parametrach wyznaczonych zgodnie z twierdzeniem
Thevenina.
Mamy więc do rozważenia obwód:
Kreskowana linia pokazuje sposób zastosowania
twierdzenia Thevenina po raz drugi.
W wyniku dwukrotnego zastosowania twierdzenia
Thevenina otrzymujemy obwód:
Maksymalna moc wydzielać się będzie na Rx gdy
Rx = 12 W, zaś Pmax = 14,08 W. Ponadto prąd I = 1,08 A.
Znajomość prądu I pozwala wyznaczyć pozostałe
prądy płynące w obwodzie oraz napięcie na zaciskach
źródła prądowego:
Bilans mocy:
Moc źródeł Pd = 20·0,233 + 20,5·1,5 = 35,410 W.
Moc rezystorów Pp = 0,2332·30 + 1,0832·12 +
0,652·20 + 1,52·5 = 35,403 W.
Błąd względny d = 0,020 %.
2. Pojemność jako element obwodu
elektrycznego
2.1. Definicja pojemności elektrycznej
Weźmy dwie bryły metalowe nie połączone ze sobą
i za pomocą specjalnej pompki, która potrafi
przepompowywać ładunki elektryczne,
przepompujmy swobodne elektrony
z jednej bryły na drugą.
Pomiędzy bryłami pojawi się wówczas napięcie U,
którego wartość będzie wprost proporcjonalna do
wielkości przepompowanego ładunku Q.
Współczynnik C proporcjonalności pomiędzy
ładunkiem Q a napięciem U jest właśnie pojemnością
elektryczną układu tych dwóch brył metalowych.
Pojemność C nie jest zależna od wielkości
przepompowanego ładunku. Zależy od kształtu i
wielkości brył, ich wzajemnego położenia oraz od
właściwości otoczenia (medium), w którym
umieszczone są bryły.
Jednostką pojemności jest farad (F) czyli stosunek
kulomba (C) do wolta (V). Ponieważ zaś kulomb to
amperosekunda, to farad może być wyrażony
stosunkiem sekundy do oma.
Dla przykładu wyznaczmy pojemność kondensatora
płaskiego
Kondensator płaski to fragment układu dwóch
nieskończenie wielkich równoległych metalowych płyt,
umieszczonych w odległości d od siebie, w środowisku
o przenikalności elektrycznej e.
Przeniesienie ładunków z jednej płyty na drugą w taki
sposób, by gęstość powierzchniowa ładunków na
każdej płycie miała wartość s, wytworzy w przestrzeni
otaczającej płyty, pole elektryczne.
Każda płyta wniesie do tego pala wkład o wartości:
Pomiędzy płytami natężenie pola elektrycznego będzie
sumą natężeń od obu płyt:
Różnica potencjałów, czyli napięcie pomiędzy płytami,
osiągnie więc wartość:
Rozważając fragment płyt o powierzchni S, otrzymamy
zależność pomiędzy przepompowanym pomiędzy
płytami ładunkiem Q, a napięciem w postaci:
2.2. Pojemnościowy dzielnik napięciowy
Najprostszy pojemnościowy dzielnik napięcia stanowią
dwie pojemności połączone szeregowo. Podanie na
wejściu napięcia U naładuje obie pojemności tym
samym ładunkiem Q:
Ponadto:
Potraktowanie tych równań jako układu względem
niewiadomych U1 oraz U2, prowadzi do rozwiązania:
W związku z tym ładunek na każdej pojemności:
Zaś wzór na zastępczą pojemność układu dwóch
pojemności połączonych szeregowo:
Pięciosegmentowy izolator wysokiego napięcia
Podział napięcia na segmentach izolatora
Postawimy założenie, że C1 = 2·C2.
Wówczas:
Podział napięcia na elementach izolatora
2.3. Zależność pomiędzy prądem i napięciem dla C
Natężenie prądu (krótko: prąd) jest stosunkiem porcji
ładunku elektrycznego DQ do przedziału czasu Dt,
podczas którego ten ładunek przepłynął
Tak wyrażony prąd oznacza wartość średnią za
przedział czasu Dt. Bardziej poprawną definicję prądu
przedstawia wzór powyższy przy przejściu do granicy
dla Dt → 0:
Podstawiając ładunek na pojemności
i zakładając stałość C, otrzymamy zależność między
prądem i napięciem na pojemności w postaci
Wzór ten, wbrew pozorom, nie oznacza wcale, że prąd
stały nie może przepływać przez pojemność.
Jeżeli, na przykład, napięcie na pojemności będzie
zmieniać się liniowo, to prąd doładowujący lub
rozładowujący tę pojemność, będzie prądem stałym.
2.4. Siła przyciągania się okładzin kondensatora
W polu elektrycznym siła działająca na ładunek
elektryczny jest iloczynem wartości tego ładunku i
natężenia pola w miejscu, w którym on się znajduje
Weźmy kondensator płaski o pojemności C
naładowany do napięcia U. Ładunek na każdej z
okładzin ma wartość Q = C·U. Natężenie pola
elektrycznego w miejscu, w którym jest jedna z
okładzin, wywołane ładunkiem zgromadzonym na
drugiej okładzinie, ma wartość
Siła działająca na tę okładzinę jest więc
Rozważmy następujące zadanie:
Kondensator o pojemności C1 został wstępnie
naładowany do napięcia U1 i odłączony od źródła.
Obliczyć pracę, jaką trzeba wykonać, by rozsunąć
okładziny tego kondensatora na odległość o 20%
większą od początkowej.
Rozwiązanie: w odłączonym od źródła kondensatorze
Q = const., a to oznacza F = const. Wobec tego:
Wynik ten można sprawdzić bilansując energię:
energię skupioną w polu elektrycznym naładowanego
kondensatora wyraża wzór
Rozsuwając okładziny kondensatora zmniejsza się jego
pojemność do wartości
Kondensator odłączony od źródła utrzymuje stały
ładunek (Q = const.), więc energia po rozsunięciu:
Praca wykonana podczas rozsuwania okładzin jest
różnicą energii końcowej W2 i początkowej W1:
2.5. Obwody prądu stałego z elementami RC
W obwodzie prądu stałego, w stanie ustalonym, gdy
wszystkie napięcia i prądy mają stałe wartości, prąd
przez pojemności nie przepływa.
Rozwiązując obwód elektryczny zasilany napięciem
stałym, w którym występują rezystory i pojemności,
przed wszystkim należy sprawdzić czy można w
obwodzie znaleźć połączenie galwaniczne biegunów
źródła napięciowego poprzez rezystory.
Na przykład w obwodzie:
prąd może przepływać przez szeregowo dla tego prądu
połączone rezystory R1, R2 oraz R3.
Przyjmując R1 = R3 = 100 W oraz R2 = 200 W, prąd ten
będzie miał wartość
Pozwala to obliczyć napięcia na rezystorach R2 i R3,
niezbędne do obliczenia napięć na pojemnościach.
W celu wyznaczenia napięć UC1, UC2 i UC3 zbudować
należy układ trzech równań: dwa będą bazować na
drugim prawie Kirchhoffa, trzecie zbilansuje ładunki
elektryczne w odosobnionej przestrzeni pokazanej
linią kreskowaną.
Dla C1 = C2 = 10 mF oraz C3 = 5 mF
otrzymamy rozwiązanie:
UC1 = -3 V, UC2 = 7 V oraz UC3 = 8 V.
3. Indukcyjność jako element obwodu
elektrycznego
Przed próbą zdefiniowania indukcyjności, jako
elementu obwodu elektrycznego, należy przede
wszystkim:
• rozróżnić dwa podobnie brzmiące pojęcia –
indukcja i indukcyjność,
• przypomnieć fizyczne prawo indukcji
magnetycznej Faradaya.
Indukcja magnetyczna to wielkość fizyczna
wektorowa, która charakteryzuje pole magnetyczne.
Najczęściej oznaczana jest literą B i zdefiniowana
odpowiednią zależnością pomiędzy ładunkiem, jego
prędkością i siłą, która działa na ten ładunek.
Wymiarem indukcji magnetycznej jest tesla (T), czyli
stosunek webera do metra kwadratowego. Weber (Wb)
to woltosekunda czyli iloczyn wolta i sekundy.
3.1. Definicja indukcyjności
Indukcyjność jest cechą charakteryzującą obiekt,
stanowiący element obwodu elektrycznego,
zdefiniowaną jako współczynnik proporcjonalności
pomiędzy strumieniem skojarzonym z tym obiektem a
prądem, który ten strumień wywołał.
Jednostką indukcyjności jest henr (H), czyli stosunek
webera (Wb = Vs) do ampera (A). Jak łatwo
wyznaczyć: henr to omosekunda.
Prawo indukcji elektromagnetycznej Faradaya wiąże
pole magnetyczne ze zjawiskami elektrycznymi w
sposób następujący:
Występujący w powyższym wzorze znak minus należy
traktować łącznie z obowiązującym tutaj
prawoskrętnym układem współrzędnych
Jeżeli w sytuacji pokazanej na rysunku magnetyczny
strumień j(t) będzie funkcją rosnącą (posiadającą
dodatnią pochodną), to siła elektromotoryczna
indukowana w konturze zaznaczonym okręgiem,
będzie miała wartość ujemną.
Gdyby więc wzdłuż konturu ułożyć zwój wykonany z
materiału przewodzącego, to po zwarciu jego
końcówek, w zwoju popłynie prąd w kierunku
pokazanym strzałką.
3.2. Zależność pomiędzy prądem i napięciem dla L
W celu zwiększenia indukcji pola magnetycznego a
więc również strumienia magnetycznego, nawija się
odpowiednią ilość zwojów na karkas budując solenoid.
Zastosowanie drugiego prawa Kirchhoffa pozwala
zapisać równanie
A stąd
Podsumowując
Oznacza to, że w obwodzie prądu stałego w stanie
ustalonym, gdy wszystkie napięcia i prądy występujące
w obwodzie są stałe, na indukcyjności napięcie jest
zerowe. Można to interpretować tak, jakby
indukcyjność była zwarciem.
4. Obwody z sinusoidalnymi prądami i
napięciami
Gdy przykładowo w rezystancyjnym obwodzie prądu
stałego
znamy wartości prądów I2 = 4 A oraz I3 = 3 A, to,
na podstawie pierwszego prawa Kirchhoffa, łatwo
odgadniemy ile wskazywać będzie amperomierz A1:
I1 = I2 + I3 = 7 A.
A jak to będzie w obwodzie prądu przemiennego, w
którym jeden z rezystorów zastąpimy kondensatorem?
Gdy wartości skuteczne prądów, wskazywane przez
amperomierze A2 i A3, będą przykładowo równe
I2 = 4 A oraz I3 = 3 A, to czy amperomierz A1
również wskaże I1 = 7 A?
Otóż niestety NIE!
Zanim jednak to sobie wyjaśnimy, należy zdefiniować
pojęcie wartości skutecznej prądów oraz napięć
okresowych.
Wartością skuteczną prądu okresowego, na przykład
sinusoidalnego, nazywamy taką wartość natężenia
prądu stałego, który przepływając przez rezystor
spowodowałby wydzielenie takiej samej ilości ciepła,
która wydzieli się podczas przepływu w tym samym
czasie, równym okresowi, rozważanego prądu
okresowego.
Dla prądu lub napięcia sinusoidalnego wartość
skuteczna jest pierwiastek z dwóch razy mniejsza od
amplitudy:
Przyrządy pomiarowe (amperomierze i woltomierze)
stosowane w obwodach prądu przemiennego mierzą
właśnie wartości skuteczne prądów i napięć.
Przykładowo napięcie w gniazdkach, w naszych
mieszkaniach, jest napięciem sinusoidalnym o wartości
skutecznej U = 230 V i częstotliwości f = 50 Hz.
Jego amplituda Um = 325,269 V a okres T = 20 ms.
4.1. Prawo Ohma w obwodach prądu przemiennego
Rezystory, kondensatory i cewki indukcyjne
(solenoidy) zachowują się w obwodach prądu
przemiennego (sinusoidalnego) w dość specyficzny
sposób. Dla każdego z nich wyznaczona zostanie
odpowiednia postać prawa Ohma.
W każdym przypadku prąd i napięcie będą opisane
następującymi funkcjami czasu:
Symbol w oznacza pulsację przy czym:
zaś ji oraz ju to fazy początkowe prądu i napięcia.
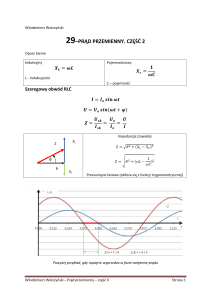
Rezystor
Przebieg wartości chwilowych prądu i napięcia oraz
tak zwany wykres fazorowy tych wielkości:
Prawo Ohma:
Solenoid
Przebieg wartości chwilowych prądu i napięcia oraz
tak zwany wykres fazorowy tych wielkości:
Prawo Ohma:
Kondensator
Przebieg wartości chwilowych prądu i napięcia oraz
tak zwany wykres fazorowy tych wielkości:
Prawo Ohma:
Właśnie relacje pomiędzy napięciem i prądem,
przedstawione na wykresach fazorowych każdego z
elementów obwodów elektrycznych, należy brać pod
uwagę przy formułowaniu praw Kirchhoffa.
Oznacza to, że:
suma prądów (w pierwszym prawie Kirchhoffa) oraz
suma napięć (w drugim), powinny być traktowane
jako sumy w sensie geometrycznym – podobnie jak to
jest, przy sumowaniu wektorów.
W przypadku rozważanego wcześniej obwodu:
kondensator i rezystor są połączone równolegle,
występuje więc na nich to samo napięcie URC.
Prądy jednak nie będą w tej samej fazie.
Przedstawia to wykres fazorowy:
Wynika z niego, że I1 = 5 A.
4.2. Rozwiązanie obwodu prądu przemiennego
Obwód elektryczny, którego schemat pokazano na
rysunku zasilono napięciem sinusoidalnym
o wartości skutecznej U = 120 V i częstotliwości
f = 50 Hz. Idealne przyrządy pomiarowe mierzące
wartości skuteczne wskazują IR = 0,4 A, IL = 0,3 A oraz
URL = 90 V. Wyznaczyć wskazanie amperomierza AC
oraz woltomierza VC.
Wykres fazorowy prądów i napięć można narysować
następująco:
Wykorzystując jedno z podstawowych twierdzeń
geometrii oraz fakt, że oba trójkąty (czerwony prądowy i niebieski - napięciowy) są trójkątami
prostokątnymi, z łatwością wyznaczymy, że
IC = 0,5 A oraz UC = 150 V.
6. Zadania do samodzielnego rozwiązania
Zadanie 1
Z jaką szybkością poruszał się dyliżans na planie
filmowym podczas kręcenia sceny wjazdu tego
dyliżansu, jeżeli na ekranie jego koła, mające po
N = 12 szprych, zdawały się być widzom nieruchome?
Średnica kół dyliżansu D = 1,2 m. Zdjęcia filmowe
wykonywano kamerą z częstotliwością
f = 24 klatki na sekundę.
Zadanie 2
Sześcian o krawędzi a = 10 cm wykonany z drewna o
gęstości r = 600 kg/m3 pływa w dużym naczyniu z
wodą częściowo zanurzony. Obliczyć pracę, jaką
trzeba wykonać wynurzając całkowicie ten sześcian z
wody. Przyjąć gęstość wody ro = 1000 kg/m3 oraz
przyspieszenie grawitacyjne g = 10 m/s2. Tarcie oraz
efekty związane z napięciem powierzchniowym
zaniedbać.
Zadanie 3
Drabina o długości L oparta jest o pionową ścianę.
Gdy dolny punkt drabiny zaczyna poruszać się ze stałą
prędkością v0 wzdłuż podłogi, górny punkt ślizga się
bez tarcia wzdłuż ściany. Wyznaczyć wartość wektora
prędkości górnego końca drabiny w chwili, gdy
drabina nachylona jest pod kątem a do podłogi.
Zadanie 4
Kondensator płaski o pojemności C1 podłączono do
źródła o napięciu U. Obliczyć pracę, jaką trzeba
wykonać, by, nie odłączając go od źródła (U = const.),
rozsunąć okładziny kondensatora na odległość o 20%
większą od początkowej.
Zadanie 5
Kondensator o pojemności C1 = 20 μF naładowany
wstępnie do napięcia U10 = 24 V połączono poprzez
rezystor o rezystancji R = 100 Ω z drugim, uprzednio
nienaładowanym, kondensatorem o pojemności
C2 = 10 μF. Ile ciepła wydzieli się na rezystorze
podczas przepływy prądu, dzięki któremu w obwodzie
wystąpi stan równowagi napięciowej w obwodzie?
Zadanie 6
Akumulator o napięciu źródłowym U i rezystancji
wewnętrznej r = 0,2 Ω włączono do obwodu
zawierającego pięć rezystorów, solenoid i kondensator.
Ładunek zgromadzony na okładkach kondensatora w
stanie ustalonym wyniósł Q = 125 nC. Obliczyć
napięcie źródłowe akumulatora, jeżeli R = 1,6 Ω,
L = 50 mH, zaś C = 40 nF.
Zadanie 7
Obwód elektryczny, którego schemat pokazano na
rysunku zasilono napięciem sinusoidalnym
o wartości skutecznej U = 100 V i częstotliwości
f = 50 Hz. Idealne przyrządy pomiarowe mierzące
wartości skuteczne wskazują IL = 2 A, IC = 1 A oraz
ULC = 80 V. Wyznaczyć wartość rezystancji R
zainstalowanej w tym obwodzie.
Dziękuję za uwagę.